北师大版九年级数学下册 第3章 《圆》压轴题型提升训练(四)(Word版 含解析)
文档属性
| 名称 | 北师大版九年级数学下册 第3章 《圆》压轴题型提升训练(四)(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 357.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-07 23:21:47 | ||
图片预览

文档简介
九年级数学下册
第3章
《圆》
压轴题型提升训练(四)
1.某数学活动小组在一次活动中,对一个数学问题作如下探究:
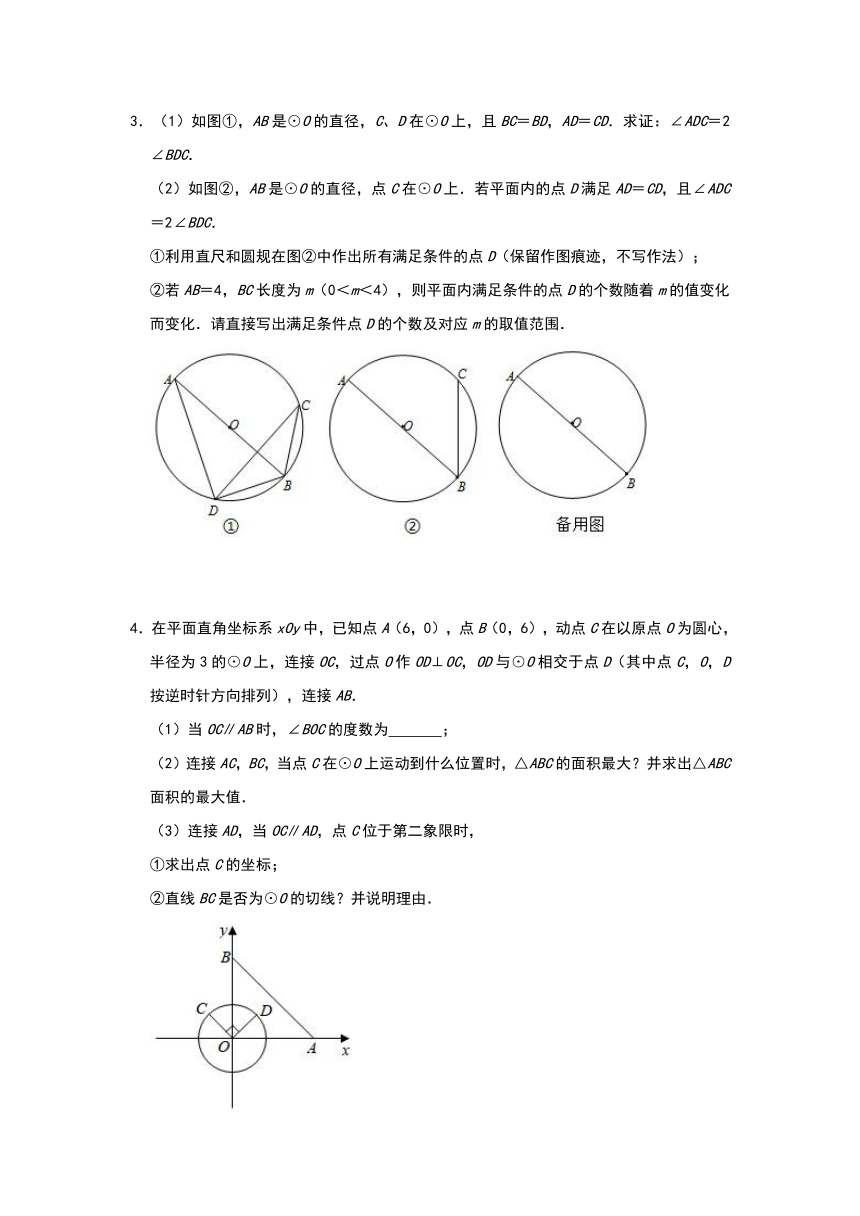
【问题探究】如图1,AD,BD为⊙O的两条弦(AD<BD),点C为的中点,过C作CE⊥BD、垂足为E.求证:BE=DE+AD.
小明同学的思路是:如图2.在BE上截取BF=AD,连接CA,CB,CD,CF…请你按照小明的思路完成上述问题的证明过程.
【结论运用】如图3,△ABC是⊙O的内接等边三角形,点D是上一点,∠ACD=45°,连接BD,CD.过点A作AE⊥CD,垂足为E.若AB=6,求△BCD的周长.
【变式探究】如图4,若将(问题探究)中“点C为的中点”改为“点C为优弧ACB的中点”,其他条件不变,请写出BE、AD、DE之间的等量关系,并加以证明.
2.如图,AB是⊙O的直径,PB,PC是⊙O的两条切线,切点分别为B,C.连接PO交⊙O于点D,交BC于点E,连接AC.
(1)求证:OE=AC;
(2)若点E是OD的中点,⊙O的半径为6,求PB的长.
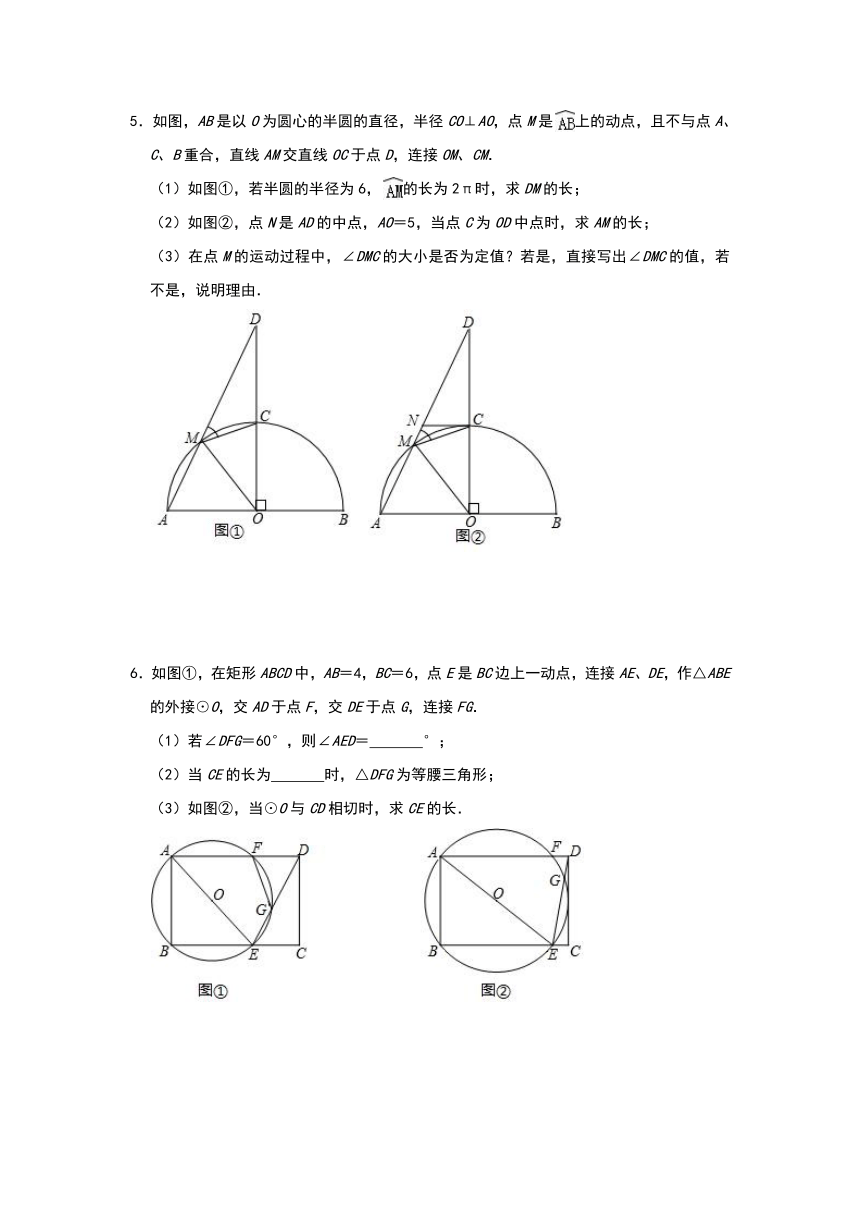
3.(1)如图①,AB是⊙O的直径,C、D在⊙O上,且BC=BD,AD=CD.求证:∠ADC=2∠BDC.
(2)如图②,AB是⊙O的直径,点C在⊙O上.若平面内的点D满足AD=CD,且∠ADC=2∠BDC.
①利用直尺和圆规在图②中作出所有满足条件的点D(保留作图痕迹,不写作法);
②若AB=4,BC长度为m(0<m<4),则平面内满足条件的点D的个数随着m的值变化而变化.请直接写出满足条件点D的个数及对应m的取值范围.
4.在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以原点O为圆心,半径为3的⊙O上,连接OC,过点O作OD⊥OC,OD与⊙O相交于点D(其中点C,O,D按逆时针方向排列),连接AB.
(1)当OC∥AB时,∠BOC的度数为
;
(2)连接AC,BC,当点C在⊙O上运动到什么位置时,△ABC的面积最大?并求出△ABC面积的最大值.
(3)连接AD,当OC∥AD,点C位于第二象限时,
①求出点C的坐标;
②直线BC是否为⊙O的切线?并说明理由.
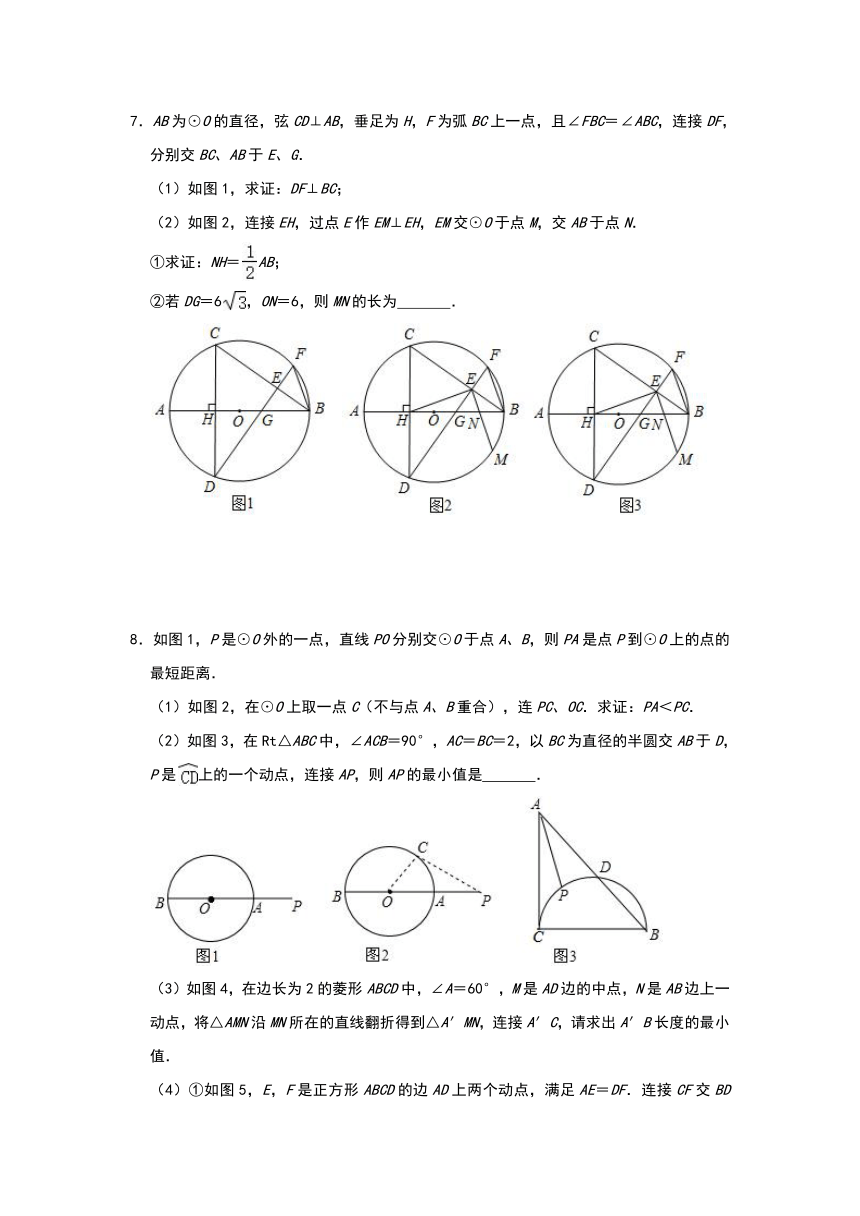
5.如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连接OM、CM.
(1)如图①,若半圆的半径为6,的长为2π时,求DM的长;
(2)如图②,点N是AD的中点,AO=5,当点C为OD中点时,求AM的长;
(3)在点M的运动过程中,∠DMC的大小是否为定值?若是,直接写出∠DMC的值,若不是,说明理由.
6.如图①,在矩形ABCD中,AB=4,BC=6,点E是BC边上一动点,连接AE、DE,作△ABE的外接⊙O,交AD于点F,交DE于点G,连接FG.
(1)若∠DFG=60°,则∠AED=
°;
(2)当CE的长为
时,△DFG为等腰三角形;
(3)如图②,当⊙O与CD相切时,求CE的长.
7.AB为⊙O的直径,弦CD⊥AB,垂足为H,F为弧BC上一点,且∠FBC=∠ABC,连接DF,分别交BC、AB于E、G.
(1)如图1,求证:DF⊥BC;
(2)如图2,连接EH,过点E作EM⊥EH,EM交⊙O于点M,交AB于点N.
①求证:NH=AB;
②若DG=6,ON=6,则MN的长为
.
8.如图1,P是⊙O外的一点,直线PO分别交⊙O于点A、B,则PA是点P到⊙O上的点的最短距离.
(1)如图2,在⊙O上取一点C(不与点A、B重合),连PC、OC.求证:PA<PC.
(2)如图3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,则AP的最小值是
.
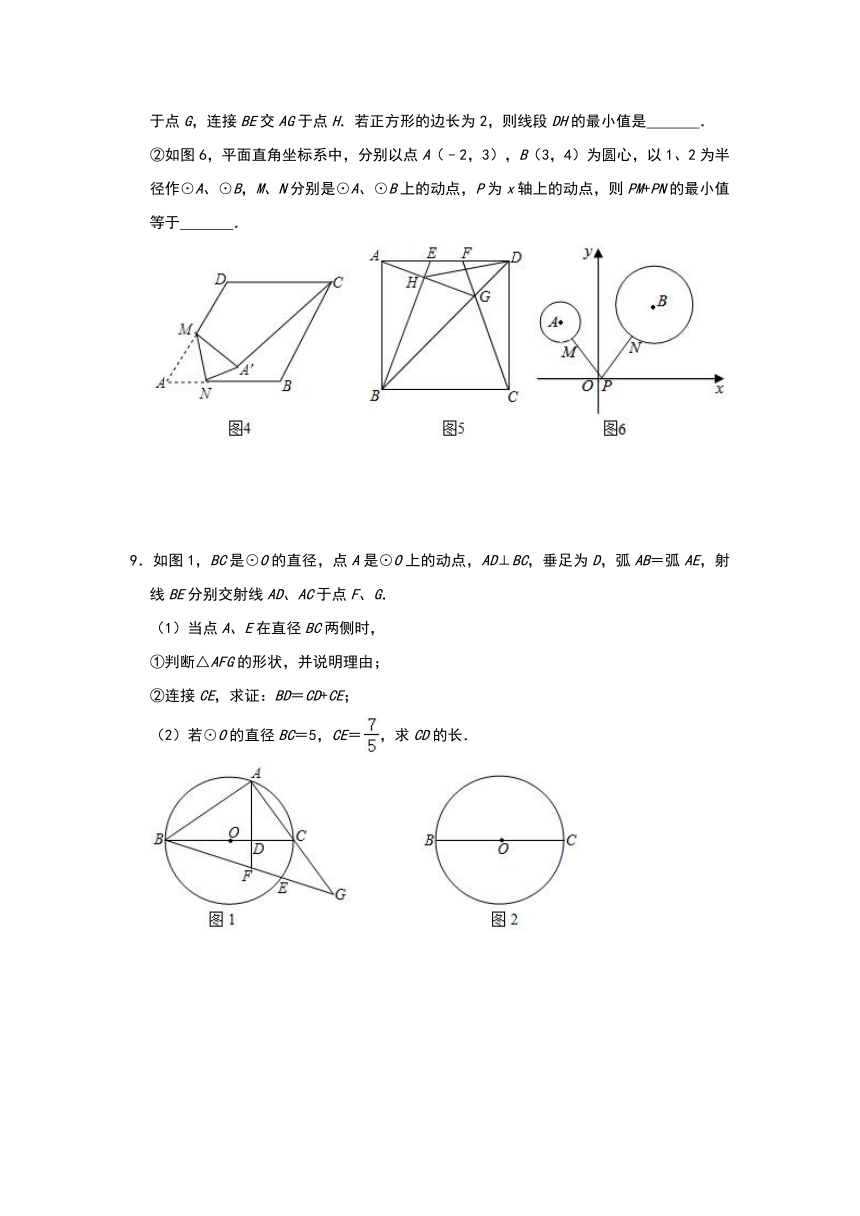
(3)如图4,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′B长度的最小值.
(4)①如图5,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH的最小值是
.
②如图6,平面直角坐标系中,分别以点A(﹣2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于
.
9.如图1,BC是⊙O的直径,点A是⊙O上的动点,AD⊥BC,垂足为D,弧AB=弧AE,射线BE分别交射线AD、AC于点F、G.
(1)当点A、E在直径BC两侧时,
①判断△AFG的形状,并说明理由;
②连接CE,求证:BD=CD+CE;
(2)若⊙O的直径BC=5,CE=,求CD的长.
10.【问题情境】如图1,C,D是∠AOB的边OA上两点,在边OB上找一点P,使得∠CPD最大.
【问题解决】小明在解决这个问题时认为:如图2,同时过C、D两点的圆与OB边相切于点P,当且仅当取此切点时,∠CPD才最大.
(1)小明证明自己结论的思路是:在射线OB上任取另一点P1(不同于切点P),证明∠CDD>∠CP1D即可请完成小明的证明;
【结论应用】请和小明一起,利用“问题情境”的结论解决下列问题:
(2)如图3,一幢楼BC上有一高为2m的信号塔AB,当观测点E在水平地面CD上,且满足CE=6时,看信号塔AB的视角(即∠AEB)最大,求楼高BC;
(3)如图4,四边形ABCD中,∠A=∠B=90°,∠BCD=60°,BC=9,对角线AC平分∠BCD.点E是BC上一点,请问当BE的长满足什么条件时,在线段AD上恰好只存在一点P,使得∠BPE=60°?(直接写出结果,不必写出解答过程)
参考答案
1.解:【问题探究】如图2,在BE上截取BF=AD,连接CA,CB,CD,CF,
∵点C为的中点,
∴=,
∴AC=BC,
由圆周角定理得,∠DAC=∠DBC,
在△DAC和△FBC中,
,
∴△DAC≌△FBC(SAS)
∴CD=CF,又CE⊥BD,
∴DE=EF,
∴BE=EF+BF=DE+AD;
【结论运用】连接AD,在CE上截取CF=AD,连接AF,
由【问题探究】可知,△DAB≌△FAC,
∴BD=CF,AD=AF,
∵AE⊥CD,
∴DE=EF,
∴EC=EF+CF=DE+BD,
∴DB+DC=2EC,
在Rt△AEC中,∠ACE=45°,
∴EC=AC=6,
∴△BCD的周长=DB+DC+BC=12+6;
【变式探究】BE+AD=DE,
理由如下:在线段DE上截取DF=AD,连接CB、CF、CD、CA,
∵点C为优弧ACB的中点,
∴=,
∴AC=CB,∠ADC=∠BDC,
在△ADC和△FDC中,
,
∴△ADC≌△FDC(SAS),
∴CA=CF,
∵CA=CB,
∴CF=CB,又CE⊥BD,
∴BE=EF,
∴DE=DF+EF=BE+AD.
2.证明:(1)∵PB,PC是⊙O的两条切线,切点分别为B,C,
∴PB=PC,∠BPO=∠CPO.
∴PO⊥BC,BE=CE.
∵OB=OA,
∴OE是△ABC的中位线,
∴OE=AC;
(2)∵PB是⊙O的切线,
∴∠OBP=90°.
由(1)可得∠BEO=90°,
∵点E是OD的中点,⊙O的半径为6,
∴OE=OD=3,
∵∠OBP=∠BEO=90°.
∴tan∠BOE==,
在Rt△BEO中,OE=3,OB=6,
∴BE=3.
∴PB=6.
3.解:(1)连接AC,
∵BD=BC,
∴,
又∵AB是直径,
∴AB垂直平分CD,
∴AC=AD,
∵CD=AD,
∴△ACD是等边三角形,
∴∠ADC=60°=∠DAC,
∵AB垂直平分CD,
∴∠BAC=∠BAD=30°=∠BDC,
∴∠ADC=2∠BDC;
(2)①如图②,以B为圆心,BC长为半径作⊙B,⊙B与AC的垂直平分线的交点为D,D';
②当⊙B与AC的垂直平分线只有一个交点时,即点D的个数为1,
∴AC=2BC,
∵AB2=AC2+BC2,
∴16=5m2,
∴m=,
∵0<m<4,
∴当0<m<时,点D的个数为0;
当m=时,点D的个数为1;
当<m<4时,点D的个数为2.
4.解:(1)∵点A(6,0),点B(0,6),
∴OA=OB=6,
∴△OAB为等腰直角三角形,
∴∠OBA=45°,
∵OC∥AB,
∴当C点在y轴左侧时,∠BOC=∠OBA=45°;
当C点在y轴右侧时,∠BOC=90°+∠OBA=135°;
综上所述,∠BOC的度数为45°或135°,
故答案为:45°或135°;
(2)∵△OAB为等腰直角三角形,
∴AB=OA=6,
∴当点C到AB的距离最大时,△ABC的面积最大,
过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,如图:
此时C点到AB的距离的最大值为CE的长,
∴OE=AB=3,
∴CE=OC+OE=3+3,
∴△ABC的面积=CE?AB=×(3+3)×6=9+18;
即当点C在⊙O上运动到第三象限的角平分线与圆的交点位置时,△ABC的面积最大,最大值为9+18;
(3)①过C点作CF⊥x轴于F,如图:
∵OC∥AD,
∴∠COF=∠DAO,
又∵∠ADO=∠CFO=90°,
∴△OCF∽Rt△AOD,
∴=,即=,
解得:CF=,
在Rt△OCF中,OF===,
∴C点坐标为(﹣,);
②直线BC是⊙O的切线.理由如下:
由①得:(﹣,),
在Rt△OCF中,OC=3,CF=,
∴CF=OC,
∴∠COF=30°,
∴∠OAD=30°,
∴∠BOC=60°,∠AOD=60°,
∵在△BOC和△AOD中,
,
∴△BOC≌△AOD(SAS),
∴∠BCO=∠ADO=90°,
∴OC⊥BC,
∴直线BC为⊙O的切线.
5.解:(1)设∠AOM=n°,
∵的长为2π,AO=6,
∴=2π,
解得:n=60,
∵OM=OA,
∴△AOM是等边三角形,
∴∠OAM=60°,AM=AO=6,
∵DO⊥AO,
∴∠D=30°,
∴AD=2AO=12,
∴DM=AD﹣AM=6;
(2)如图②,过点O作OP⊥AM于P,则AP=PM,
∵点C为OD中点,
∴CD=CO=AO=5,
∴OD=10,
∵CO⊥AO,
∴∠AOD=90°,
在Rt△AOD中,由勾股定理得,AD===5,
∵∠PAO=∠OAD,∠APO=∠AOD=90°,
∴△APO∽△AOD,
∴=,
即=,
解得:AP=,
∴AM=2;
(3)∠DMC是定值,为45°,理由如下:
∵CO⊥OB,OC=OB,
∴∠ABC=45°,
当点M在上时,如图①,连接BC,
∵四边形ABCM为圆内接四边形,
∴∠DMC=∠ABC=45°,
当点M在上时,如图③,连接BC,
由圆周角定理得,∠DMC=∠ABC=45°,
综上所述,∠DMC是定值,为45°.
6.解:(1)∵四边形AEGF是⊙O的内接四边形,
∴∠AED=∠DFG=60°,
故答案为:60;
(2)连接EF,如图①所示:
∵四边形FGEA是⊙O的内接四边形,
∴∠DGF=∠DAE,
又∠GDF=∠ADE,
∴△DFG∽△DEA,
∴当△DEA为等腰三角形时,△DFG为等腰三角形,
∵四边形ABCD是矩形,AB=4,BC=6,
∴CD=AB=4,AD=BC=6,∠BAD=∠ABC=∠BCD=∠ADC=90°,
∵⊙O是△ABE的外接圆,∠ABE=90°,
∴AE是⊙O的直径,
∴∠AFE=90°,
∴∠DFE=180°﹣∠AFE=180°﹣90°=90°,
∴∠CDF=∠DCE=∠DFE=90°,
∴四边形DCEF是矩形,
∴DF=CE,EF=CD=4,
若△AED为等腰三角形,分三种情况:
①当AE=DE时,
∵∠AFE=90°,
∴EF⊥AD,
∴AF=DF=AD=3,
∴CE=DF=3;
②当AE=AD=6时,
在Rt△ABE中,由勾股定理得:BE===2,
∴CE=BC﹣CE=6﹣2;
③当DE=DA=6时,
在Rt△DCE中,由勾股定理得:CE===2;
综上所述,当BE的长为3或6﹣2或2时,△DFG为等腰三角形,
故答案为:3或6﹣2或2;
(3)过O作OH⊥AB于点H,如图②所示:
则OH∥AD∥CE,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴AE为⊙O的直径,
∴OA=OE,
∴OH是梯形ADCE的中位线,
∴OH=(AD+CE),
∴2OH=AD+CE,
∵⊙O与CD相切,
∴H为切点,
∴OH=OA,
∴AE=2OH=AD+CE=6+CE,
在Rt△ABE中,由勾股定理得:AB2+BE2=AE2,
即42+(6﹣CE)2=(6+CE)2,
解得:CE=.
7.(1)证明:∵CD⊥AB,
∴∠BHC=90°,
∴∠C+∠ABC=90°,
∵∠FBC=∠ABC,∠F=∠C,
∴∠F+∠FBC=90°,
∴∠BEF=90°,
∴DF⊥BC.
(2)①证明:连接OC.
∵OC=OB,
∴∠OCB=∠OBC=∠D,
∵CD⊥AB,
∴∠CHO=90°,CH=DH,
∵∠CED=∠BEF=90°,
∴HE=CD=CH=DH,
∴∠D=∠HED,
∴∠OCB=∠HED,
∵EM⊥EH,
∴∠HEN=∠HED+∠DEN=90°,
∵∠DEN+∠BEN=∠BED=90°,
∴∠HED=∠BEN,
∴∠OCB=∠BEN,
∴OC∥EM,
∴∠COH=∠HNE,
在△COH与△HNE中,
,
∴△COH≌△HNE(AAS),
∴CO=NH,
∴NH=AB.
(3)解:连接OM,过点M作MP⊥AB于点P.
∵∠HEN=∠HEG+∠GEN=90°,
∠D+∠DGH=90°,
∠D=∠HEG,
∴∠GEN=∠DGH,
∵∠DGH=∠EGN,
∴∠GEN=∠EGN,
∴EN=GN,
∵△COH≌△HNE,
∴OH=NE=GN,
∴HG=OH+OG=GN+OG=ON=6,
∵DG=6,∠DHG=90°,
∴HE=CH=DH===6,
∵△DHG∽△BHC,
∴=,
∴BH===12,
设OB=OC=r,则OH=BH﹣OB=12﹣r,
∵OH2+CH2=OC2,
∴(12﹣r)2+(6)2=r2,
解得:r=9,
∴OM=9,NH=AB=9,NG=EN=BN=3,
∵∠MNP=∠HNE,∠MPN=∠HEP=90°,
∴△MNP∽△HNE,
∴==,
设MN=a,则NP==,MP==a,
∴OP=ON+NP=6+,
∵OP2+MP2=OM2,
∴(6+)2+(a)2=92,
解得:a1=﹣9(舍去),a2=5,
∴MN=5.
故答案为5.
8.(1)证明:如图2,在⊙O上任取一点C(不为点A、B),连接PC、OC.
∵PO<PC+OC,PO=PA+OA,OA=OC,
∴PA<PC,
∴PA是点P到⊙O上的点的最短距离;
(2)解:连接AO与⊙O相交于点P,如图3,由已知定理可知,此时AP最短,
∵∠ACB=90°,AC=BC=2,BC为直径,
∴PO=CO=1,
∴AO==,
∴AP=﹣1,
故答案为:﹣1;
(3)解:如图4,由折叠知A′M=AM,又M是AD的中点,可得MA=MA′=MD,
故点A′在以AD为直径的圆上,
由模型可知,当点A′在BM上时,A′B长度取得最小值,
∵边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,
∴BM==,
故A′B的最小值为:﹣1;
(4)①解:在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴∠1=∠2,
在△ADG和△CDG中,
,
∴△ADG≌△CDG(SAS),
∴∠2=∠3,
∴∠1=∠3,
∵∠BAH+∠3=∠BAD=90°,
∴∠1+∠BAH=90°,
∴∠AHB=180°﹣90°=90°,
取AB的中点O,连接OH、OD,
则OH=AO=AB=1,
在Rt△AOD中,OD==,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
DH最小值=OD﹣OH=﹣1.
故答案为:﹣1;
②解:作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图6,
则此时PM+PN最小,
∵点A坐标(﹣2,3),
∴点A′坐标(﹣2,﹣3),
∵点B(3,4),
∴A′B==,
∴MN=A′B﹣BN﹣A′M=﹣2﹣1=﹣3,
∴PM+PN的最小值为﹣3.
故答案为:﹣3.
9.(1)①解:等腰三角形,理由如下;
∵BC为⊙O的直径,
∴∠BAC=90°,
∴∠ABE+∠AGB=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠ACD+∠DAC=90°,
∵弧AE=弧AB,
∴∠ABE=∠ACD,
∴∠DAC=∠AGB,
∴FA=FG,
∴△FAG是等腰三角形;
②证明:在CB上截取DH=CD,连接AH、AE,如图1所示:
∵AD⊥BC,
∴AH=AC,
∴∠AHC=∠ACH,
∵弧AB=弧AE,
∴∠AEB=∠ABE,AE=AB,
∵∠AHC+∠ACH+∠HAC=180°,∠ABE+∠AEB+∠BAE=180°,∠ACB=∠AEB,
∴∠HAC=∠BAE,
∴∠CAE=∠HAB,
∴△ACE≌△AHB(SAS),
∴CE=HB,
∵BD=DH+HB,
∴BD=CD+CE;
(2)解:分两种情况:
①当点A、E在直径BC两侧时,如图1所示:
由(1)得:BD=CD+CE=CD+,
∵BD+CD=BC=5,
∴CD++CD=5,
解得:CD=;
②当点A、E在直径BC同侧时,
在CB上截取DH=BD,连接AH、AE,如图2所示:
∵弧AB=弧AE,
∴∠ACE=∠ACH=∠AEB,AB=AE,
∵AD⊥BC,
∴∠ABC+∠BAD=90°,
∴∠BAD=∠HAD,
∵BC是⊙O的直径,
∴∠BEC=∠BAC=90°,
∴∠ABC+∠ACB=90°,
∴∠BAD=∠ACB,
∵∠AHC=∠ADH+∠HAD=90°+∠HAD,∠AEC=∠BEC+∠AEB,
∴∠AHC=∠AEC,
在△AHC和△AEC中,
,
∴△AHC≌△AEC(AAS),
∴CH=CE=,
∴DH=BD=(BC﹣CH)=(5﹣)=,
∴CD=CH+DH=;
综上所述,CD的长为或.
10.解:(1)在射线OB上任取另一点P1(不同于切点P),连接P1D,交圆于点E,连接P1C,CD.
∵∠CPD=∠CED,∠CED>∠CP1D,
∴∠CPD>∠CP1D;
(2)作AB垂直平分线OF,过点E作OE⊥CD,连接OB.
则有∠CFO=∠CEO=∠C=90°,
∴四边形OECF为矩形.
∴OF=CE=6,
∵看信号塔AB的视角(即∠AEB)最大,
∴以O为圆心OB为半径的圆O,必与CD切于点E,
即OB=OE.
∵AB=2,
∴BF=1.
设BC=x米,则OB=OE=CF=(1+x)米.
在直角三角形OBF中,有OB2=BF2+OF2,即(1+x)2=(6)2+1,
解得x=18或﹣20(舍去),
所以楼高BC为18米;
(3)如图3,∵∠BCD=60°,BC=9,对角线AC平分∠BCD,
则∠ACB=30°,则AB=BCtan30°=9?=3,则AC=2AB=6,
∵AD∥BC,则∠ACB=∠DAC=∠ACD=30°,
故△ADC为底角为30°、底边为6的等腰三角形,
则AD=CD=AC÷cos30°=×6÷=6;
①当以BE为弦的圆与AD相切时,符合题设要求,
则点P在AD上,∠BPE=60°,连接OP并延长PO交BC于点F,则PF⊥BC,连接OB、OE,
则∠BOF=2∠BPO=60°,
则Rt△BOF中,∠OBF=30°,设圆的半径为r(以下圆的半径均用r表示),则OF=r,
则AB=PF=r+r=3,解得r=2,
在Rt△BOF中,BF=BO?cos30°=2?=3=BE,
故BE=6;
②如图4,当以BE为弦的圆过点D时,符合题设要求,即点P、D重合,
连接BO并延长交CD于点G,
同理可得△BOE为底角为30°的等腰三角形,
则∠GBC=30°,
而∠DCB=60°,故∠BGC=90°,即BG⊥CD,
在Rt△BCG中,CG=BC=,BG=BCcos30°=,
则GD=CD﹣CG=6﹣=,OG=BG﹣r=﹣r,
连接OD、OE,
在Rt△ODG中,OD2=DG2+OG2,即r2=(﹣r)2+()2,
解得r=,
由①知,BE=2rcos30°=2××=7;
③当以BE为弦的圆过点A时,此时点A为临界点,
连接AE,
∴∠ABC=90°,
故AE过点O,
同理可得:∠AEB=30°,
则AE=2AB=6=2r,
则BE=2rcos30°=6?=9.
综上,BE=6或7<BE≤9时,符合要求.
第3章
《圆》
压轴题型提升训练(四)
1.某数学活动小组在一次活动中,对一个数学问题作如下探究:
【问题探究】如图1,AD,BD为⊙O的两条弦(AD<BD),点C为的中点,过C作CE⊥BD、垂足为E.求证:BE=DE+AD.
小明同学的思路是:如图2.在BE上截取BF=AD,连接CA,CB,CD,CF…请你按照小明的思路完成上述问题的证明过程.
【结论运用】如图3,△ABC是⊙O的内接等边三角形,点D是上一点,∠ACD=45°,连接BD,CD.过点A作AE⊥CD,垂足为E.若AB=6,求△BCD的周长.
【变式探究】如图4,若将(问题探究)中“点C为的中点”改为“点C为优弧ACB的中点”,其他条件不变,请写出BE、AD、DE之间的等量关系,并加以证明.
2.如图,AB是⊙O的直径,PB,PC是⊙O的两条切线,切点分别为B,C.连接PO交⊙O于点D,交BC于点E,连接AC.
(1)求证:OE=AC;
(2)若点E是OD的中点,⊙O的半径为6,求PB的长.
3.(1)如图①,AB是⊙O的直径,C、D在⊙O上,且BC=BD,AD=CD.求证:∠ADC=2∠BDC.
(2)如图②,AB是⊙O的直径,点C在⊙O上.若平面内的点D满足AD=CD,且∠ADC=2∠BDC.
①利用直尺和圆规在图②中作出所有满足条件的点D(保留作图痕迹,不写作法);
②若AB=4,BC长度为m(0<m<4),则平面内满足条件的点D的个数随着m的值变化而变化.请直接写出满足条件点D的个数及对应m的取值范围.
4.在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以原点O为圆心,半径为3的⊙O上,连接OC,过点O作OD⊥OC,OD与⊙O相交于点D(其中点C,O,D按逆时针方向排列),连接AB.
(1)当OC∥AB时,∠BOC的度数为
;
(2)连接AC,BC,当点C在⊙O上运动到什么位置时,△ABC的面积最大?并求出△ABC面积的最大值.
(3)连接AD,当OC∥AD,点C位于第二象限时,
①求出点C的坐标;
②直线BC是否为⊙O的切线?并说明理由.
5.如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连接OM、CM.
(1)如图①,若半圆的半径为6,的长为2π时,求DM的长;
(2)如图②,点N是AD的中点,AO=5,当点C为OD中点时,求AM的长;
(3)在点M的运动过程中,∠DMC的大小是否为定值?若是,直接写出∠DMC的值,若不是,说明理由.
6.如图①,在矩形ABCD中,AB=4,BC=6,点E是BC边上一动点,连接AE、DE,作△ABE的外接⊙O,交AD于点F,交DE于点G,连接FG.
(1)若∠DFG=60°,则∠AED=
°;
(2)当CE的长为
时,△DFG为等腰三角形;
(3)如图②,当⊙O与CD相切时,求CE的长.
7.AB为⊙O的直径,弦CD⊥AB,垂足为H,F为弧BC上一点,且∠FBC=∠ABC,连接DF,分别交BC、AB于E、G.
(1)如图1,求证:DF⊥BC;
(2)如图2,连接EH,过点E作EM⊥EH,EM交⊙O于点M,交AB于点N.
①求证:NH=AB;
②若DG=6,ON=6,则MN的长为
.
8.如图1,P是⊙O外的一点,直线PO分别交⊙O于点A、B,则PA是点P到⊙O上的点的最短距离.
(1)如图2,在⊙O上取一点C(不与点A、B重合),连PC、OC.求证:PA<PC.
(2)如图3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,则AP的最小值是
.
(3)如图4,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′B长度的最小值.
(4)①如图5,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH的最小值是
.
②如图6,平面直角坐标系中,分别以点A(﹣2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于
.
9.如图1,BC是⊙O的直径,点A是⊙O上的动点,AD⊥BC,垂足为D,弧AB=弧AE,射线BE分别交射线AD、AC于点F、G.
(1)当点A、E在直径BC两侧时,
①判断△AFG的形状,并说明理由;
②连接CE,求证:BD=CD+CE;
(2)若⊙O的直径BC=5,CE=,求CD的长.
10.【问题情境】如图1,C,D是∠AOB的边OA上两点,在边OB上找一点P,使得∠CPD最大.
【问题解决】小明在解决这个问题时认为:如图2,同时过C、D两点的圆与OB边相切于点P,当且仅当取此切点时,∠CPD才最大.
(1)小明证明自己结论的思路是:在射线OB上任取另一点P1(不同于切点P),证明∠CDD>∠CP1D即可请完成小明的证明;
【结论应用】请和小明一起,利用“问题情境”的结论解决下列问题:
(2)如图3,一幢楼BC上有一高为2m的信号塔AB,当观测点E在水平地面CD上,且满足CE=6时,看信号塔AB的视角(即∠AEB)最大,求楼高BC;
(3)如图4,四边形ABCD中,∠A=∠B=90°,∠BCD=60°,BC=9,对角线AC平分∠BCD.点E是BC上一点,请问当BE的长满足什么条件时,在线段AD上恰好只存在一点P,使得∠BPE=60°?(直接写出结果,不必写出解答过程)
参考答案
1.解:【问题探究】如图2,在BE上截取BF=AD,连接CA,CB,CD,CF,
∵点C为的中点,
∴=,
∴AC=BC,
由圆周角定理得,∠DAC=∠DBC,
在△DAC和△FBC中,
,
∴△DAC≌△FBC(SAS)
∴CD=CF,又CE⊥BD,
∴DE=EF,
∴BE=EF+BF=DE+AD;
【结论运用】连接AD,在CE上截取CF=AD,连接AF,
由【问题探究】可知,△DAB≌△FAC,
∴BD=CF,AD=AF,
∵AE⊥CD,
∴DE=EF,
∴EC=EF+CF=DE+BD,
∴DB+DC=2EC,
在Rt△AEC中,∠ACE=45°,
∴EC=AC=6,
∴△BCD的周长=DB+DC+BC=12+6;
【变式探究】BE+AD=DE,
理由如下:在线段DE上截取DF=AD,连接CB、CF、CD、CA,
∵点C为优弧ACB的中点,
∴=,
∴AC=CB,∠ADC=∠BDC,
在△ADC和△FDC中,
,
∴△ADC≌△FDC(SAS),
∴CA=CF,
∵CA=CB,
∴CF=CB,又CE⊥BD,
∴BE=EF,
∴DE=DF+EF=BE+AD.
2.证明:(1)∵PB,PC是⊙O的两条切线,切点分别为B,C,
∴PB=PC,∠BPO=∠CPO.
∴PO⊥BC,BE=CE.
∵OB=OA,
∴OE是△ABC的中位线,
∴OE=AC;
(2)∵PB是⊙O的切线,
∴∠OBP=90°.
由(1)可得∠BEO=90°,
∵点E是OD的中点,⊙O的半径为6,
∴OE=OD=3,
∵∠OBP=∠BEO=90°.
∴tan∠BOE==,
在Rt△BEO中,OE=3,OB=6,
∴BE=3.
∴PB=6.
3.解:(1)连接AC,
∵BD=BC,
∴,
又∵AB是直径,
∴AB垂直平分CD,
∴AC=AD,
∵CD=AD,
∴△ACD是等边三角形,
∴∠ADC=60°=∠DAC,
∵AB垂直平分CD,
∴∠BAC=∠BAD=30°=∠BDC,
∴∠ADC=2∠BDC;
(2)①如图②,以B为圆心,BC长为半径作⊙B,⊙B与AC的垂直平分线的交点为D,D';
②当⊙B与AC的垂直平分线只有一个交点时,即点D的个数为1,
∴AC=2BC,
∵AB2=AC2+BC2,
∴16=5m2,
∴m=,
∵0<m<4,
∴当0<m<时,点D的个数为0;
当m=时,点D的个数为1;
当<m<4时,点D的个数为2.
4.解:(1)∵点A(6,0),点B(0,6),
∴OA=OB=6,
∴△OAB为等腰直角三角形,
∴∠OBA=45°,
∵OC∥AB,
∴当C点在y轴左侧时,∠BOC=∠OBA=45°;
当C点在y轴右侧时,∠BOC=90°+∠OBA=135°;
综上所述,∠BOC的度数为45°或135°,
故答案为:45°或135°;
(2)∵△OAB为等腰直角三角形,
∴AB=OA=6,
∴当点C到AB的距离最大时,△ABC的面积最大,
过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,如图:
此时C点到AB的距离的最大值为CE的长,
∴OE=AB=3,
∴CE=OC+OE=3+3,
∴△ABC的面积=CE?AB=×(3+3)×6=9+18;
即当点C在⊙O上运动到第三象限的角平分线与圆的交点位置时,△ABC的面积最大,最大值为9+18;
(3)①过C点作CF⊥x轴于F,如图:
∵OC∥AD,
∴∠COF=∠DAO,
又∵∠ADO=∠CFO=90°,
∴△OCF∽Rt△AOD,
∴=,即=,
解得:CF=,
在Rt△OCF中,OF===,
∴C点坐标为(﹣,);
②直线BC是⊙O的切线.理由如下:
由①得:(﹣,),
在Rt△OCF中,OC=3,CF=,
∴CF=OC,
∴∠COF=30°,
∴∠OAD=30°,
∴∠BOC=60°,∠AOD=60°,
∵在△BOC和△AOD中,
,
∴△BOC≌△AOD(SAS),
∴∠BCO=∠ADO=90°,
∴OC⊥BC,
∴直线BC为⊙O的切线.
5.解:(1)设∠AOM=n°,
∵的长为2π,AO=6,
∴=2π,
解得:n=60,
∵OM=OA,
∴△AOM是等边三角形,
∴∠OAM=60°,AM=AO=6,
∵DO⊥AO,
∴∠D=30°,
∴AD=2AO=12,
∴DM=AD﹣AM=6;
(2)如图②,过点O作OP⊥AM于P,则AP=PM,
∵点C为OD中点,
∴CD=CO=AO=5,
∴OD=10,
∵CO⊥AO,
∴∠AOD=90°,
在Rt△AOD中,由勾股定理得,AD===5,
∵∠PAO=∠OAD,∠APO=∠AOD=90°,
∴△APO∽△AOD,
∴=,
即=,
解得:AP=,
∴AM=2;
(3)∠DMC是定值,为45°,理由如下:
∵CO⊥OB,OC=OB,
∴∠ABC=45°,
当点M在上时,如图①,连接BC,
∵四边形ABCM为圆内接四边形,
∴∠DMC=∠ABC=45°,
当点M在上时,如图③,连接BC,
由圆周角定理得,∠DMC=∠ABC=45°,
综上所述,∠DMC是定值,为45°.
6.解:(1)∵四边形AEGF是⊙O的内接四边形,
∴∠AED=∠DFG=60°,
故答案为:60;
(2)连接EF,如图①所示:
∵四边形FGEA是⊙O的内接四边形,
∴∠DGF=∠DAE,
又∠GDF=∠ADE,
∴△DFG∽△DEA,
∴当△DEA为等腰三角形时,△DFG为等腰三角形,
∵四边形ABCD是矩形,AB=4,BC=6,
∴CD=AB=4,AD=BC=6,∠BAD=∠ABC=∠BCD=∠ADC=90°,
∵⊙O是△ABE的外接圆,∠ABE=90°,
∴AE是⊙O的直径,
∴∠AFE=90°,
∴∠DFE=180°﹣∠AFE=180°﹣90°=90°,
∴∠CDF=∠DCE=∠DFE=90°,
∴四边形DCEF是矩形,
∴DF=CE,EF=CD=4,
若△AED为等腰三角形,分三种情况:
①当AE=DE时,
∵∠AFE=90°,
∴EF⊥AD,
∴AF=DF=AD=3,
∴CE=DF=3;
②当AE=AD=6时,
在Rt△ABE中,由勾股定理得:BE===2,
∴CE=BC﹣CE=6﹣2;
③当DE=DA=6时,
在Rt△DCE中,由勾股定理得:CE===2;
综上所述,当BE的长为3或6﹣2或2时,△DFG为等腰三角形,
故答案为:3或6﹣2或2;
(3)过O作OH⊥AB于点H,如图②所示:
则OH∥AD∥CE,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴AE为⊙O的直径,
∴OA=OE,
∴OH是梯形ADCE的中位线,
∴OH=(AD+CE),
∴2OH=AD+CE,
∵⊙O与CD相切,
∴H为切点,
∴OH=OA,
∴AE=2OH=AD+CE=6+CE,
在Rt△ABE中,由勾股定理得:AB2+BE2=AE2,
即42+(6﹣CE)2=(6+CE)2,
解得:CE=.
7.(1)证明:∵CD⊥AB,
∴∠BHC=90°,
∴∠C+∠ABC=90°,
∵∠FBC=∠ABC,∠F=∠C,
∴∠F+∠FBC=90°,
∴∠BEF=90°,
∴DF⊥BC.
(2)①证明:连接OC.
∵OC=OB,
∴∠OCB=∠OBC=∠D,
∵CD⊥AB,
∴∠CHO=90°,CH=DH,
∵∠CED=∠BEF=90°,
∴HE=CD=CH=DH,
∴∠D=∠HED,
∴∠OCB=∠HED,
∵EM⊥EH,
∴∠HEN=∠HED+∠DEN=90°,
∵∠DEN+∠BEN=∠BED=90°,
∴∠HED=∠BEN,
∴∠OCB=∠BEN,
∴OC∥EM,
∴∠COH=∠HNE,
在△COH与△HNE中,
,
∴△COH≌△HNE(AAS),
∴CO=NH,
∴NH=AB.
(3)解:连接OM,过点M作MP⊥AB于点P.
∵∠HEN=∠HEG+∠GEN=90°,
∠D+∠DGH=90°,
∠D=∠HEG,
∴∠GEN=∠DGH,
∵∠DGH=∠EGN,
∴∠GEN=∠EGN,
∴EN=GN,
∵△COH≌△HNE,
∴OH=NE=GN,
∴HG=OH+OG=GN+OG=ON=6,
∵DG=6,∠DHG=90°,
∴HE=CH=DH===6,
∵△DHG∽△BHC,
∴=,
∴BH===12,
设OB=OC=r,则OH=BH﹣OB=12﹣r,
∵OH2+CH2=OC2,
∴(12﹣r)2+(6)2=r2,
解得:r=9,
∴OM=9,NH=AB=9,NG=EN=BN=3,
∵∠MNP=∠HNE,∠MPN=∠HEP=90°,
∴△MNP∽△HNE,
∴==,
设MN=a,则NP==,MP==a,
∴OP=ON+NP=6+,
∵OP2+MP2=OM2,
∴(6+)2+(a)2=92,
解得:a1=﹣9(舍去),a2=5,
∴MN=5.
故答案为5.
8.(1)证明:如图2,在⊙O上任取一点C(不为点A、B),连接PC、OC.
∵PO<PC+OC,PO=PA+OA,OA=OC,
∴PA<PC,
∴PA是点P到⊙O上的点的最短距离;
(2)解:连接AO与⊙O相交于点P,如图3,由已知定理可知,此时AP最短,
∵∠ACB=90°,AC=BC=2,BC为直径,
∴PO=CO=1,
∴AO==,
∴AP=﹣1,
故答案为:﹣1;
(3)解:如图4,由折叠知A′M=AM,又M是AD的中点,可得MA=MA′=MD,
故点A′在以AD为直径的圆上,
由模型可知,当点A′在BM上时,A′B长度取得最小值,
∵边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,
∴BM==,
故A′B的最小值为:﹣1;
(4)①解:在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴∠1=∠2,
在△ADG和△CDG中,
,
∴△ADG≌△CDG(SAS),
∴∠2=∠3,
∴∠1=∠3,
∵∠BAH+∠3=∠BAD=90°,
∴∠1+∠BAH=90°,
∴∠AHB=180°﹣90°=90°,
取AB的中点O,连接OH、OD,
则OH=AO=AB=1,
在Rt△AOD中,OD==,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
DH最小值=OD﹣OH=﹣1.
故答案为:﹣1;
②解:作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图6,
则此时PM+PN最小,
∵点A坐标(﹣2,3),
∴点A′坐标(﹣2,﹣3),
∵点B(3,4),
∴A′B==,
∴MN=A′B﹣BN﹣A′M=﹣2﹣1=﹣3,
∴PM+PN的最小值为﹣3.
故答案为:﹣3.
9.(1)①解:等腰三角形,理由如下;
∵BC为⊙O的直径,
∴∠BAC=90°,
∴∠ABE+∠AGB=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠ACD+∠DAC=90°,
∵弧AE=弧AB,
∴∠ABE=∠ACD,
∴∠DAC=∠AGB,
∴FA=FG,
∴△FAG是等腰三角形;
②证明:在CB上截取DH=CD,连接AH、AE,如图1所示:
∵AD⊥BC,
∴AH=AC,
∴∠AHC=∠ACH,
∵弧AB=弧AE,
∴∠AEB=∠ABE,AE=AB,
∵∠AHC+∠ACH+∠HAC=180°,∠ABE+∠AEB+∠BAE=180°,∠ACB=∠AEB,
∴∠HAC=∠BAE,
∴∠CAE=∠HAB,
∴△ACE≌△AHB(SAS),
∴CE=HB,
∵BD=DH+HB,
∴BD=CD+CE;
(2)解:分两种情况:
①当点A、E在直径BC两侧时,如图1所示:
由(1)得:BD=CD+CE=CD+,
∵BD+CD=BC=5,
∴CD++CD=5,
解得:CD=;
②当点A、E在直径BC同侧时,
在CB上截取DH=BD,连接AH、AE,如图2所示:
∵弧AB=弧AE,
∴∠ACE=∠ACH=∠AEB,AB=AE,
∵AD⊥BC,
∴∠ABC+∠BAD=90°,
∴∠BAD=∠HAD,
∵BC是⊙O的直径,
∴∠BEC=∠BAC=90°,
∴∠ABC+∠ACB=90°,
∴∠BAD=∠ACB,
∵∠AHC=∠ADH+∠HAD=90°+∠HAD,∠AEC=∠BEC+∠AEB,
∴∠AHC=∠AEC,
在△AHC和△AEC中,
,
∴△AHC≌△AEC(AAS),
∴CH=CE=,
∴DH=BD=(BC﹣CH)=(5﹣)=,
∴CD=CH+DH=;
综上所述,CD的长为或.
10.解:(1)在射线OB上任取另一点P1(不同于切点P),连接P1D,交圆于点E,连接P1C,CD.
∵∠CPD=∠CED,∠CED>∠CP1D,
∴∠CPD>∠CP1D;
(2)作AB垂直平分线OF,过点E作OE⊥CD,连接OB.
则有∠CFO=∠CEO=∠C=90°,
∴四边形OECF为矩形.
∴OF=CE=6,
∵看信号塔AB的视角(即∠AEB)最大,
∴以O为圆心OB为半径的圆O,必与CD切于点E,
即OB=OE.
∵AB=2,
∴BF=1.
设BC=x米,则OB=OE=CF=(1+x)米.
在直角三角形OBF中,有OB2=BF2+OF2,即(1+x)2=(6)2+1,
解得x=18或﹣20(舍去),
所以楼高BC为18米;
(3)如图3,∵∠BCD=60°,BC=9,对角线AC平分∠BCD,
则∠ACB=30°,则AB=BCtan30°=9?=3,则AC=2AB=6,
∵AD∥BC,则∠ACB=∠DAC=∠ACD=30°,
故△ADC为底角为30°、底边为6的等腰三角形,
则AD=CD=AC÷cos30°=×6÷=6;
①当以BE为弦的圆与AD相切时,符合题设要求,
则点P在AD上,∠BPE=60°,连接OP并延长PO交BC于点F,则PF⊥BC,连接OB、OE,
则∠BOF=2∠BPO=60°,
则Rt△BOF中,∠OBF=30°,设圆的半径为r(以下圆的半径均用r表示),则OF=r,
则AB=PF=r+r=3,解得r=2,
在Rt△BOF中,BF=BO?cos30°=2?=3=BE,
故BE=6;
②如图4,当以BE为弦的圆过点D时,符合题设要求,即点P、D重合,
连接BO并延长交CD于点G,
同理可得△BOE为底角为30°的等腰三角形,
则∠GBC=30°,
而∠DCB=60°,故∠BGC=90°,即BG⊥CD,
在Rt△BCG中,CG=BC=,BG=BCcos30°=,
则GD=CD﹣CG=6﹣=,OG=BG﹣r=﹣r,
连接OD、OE,
在Rt△ODG中,OD2=DG2+OG2,即r2=(﹣r)2+()2,
解得r=,
由①知,BE=2rcos30°=2××=7;
③当以BE为弦的圆过点A时,此时点A为临界点,
连接AE,
∴∠ABC=90°,
故AE过点O,
同理可得:∠AEB=30°,
则AE=2AB=6=2r,
则BE=2rcos30°=6?=9.
综上,BE=6或7<BE≤9时,符合要求.
