初中数学华东师大版八年级下册17.5 实践与探索课件(共26张PPT)
文档属性
| 名称 | 初中数学华东师大版八年级下册17.5 实践与探索课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 00:00:00 | ||
图片预览




文档简介
反比例函数的应用
——与面积有关的问题
学习目标
知识目标:掌握利用反比例函数解析式中比例系数解决矩形,三角形面积问题。
能力目标:培养自己自主探究,合作交流 的能力。
情感态度:通过讨论交流,合作学习,培养自己研究问题,解决问题的能力。
P(m,n)
如图,点P(m,n)是反比例函数 图象上的一点,过点P分别向x轴、y轴作垂线,垂足分别是点A、B,则S矩形OAPB=________.
x
y
O
A
B
过双曲线上任意一点作x轴、y轴的垂线,所得矩形的面积S为定值,即S=|k|.
探究1
结论1:
|k|
x
y
O
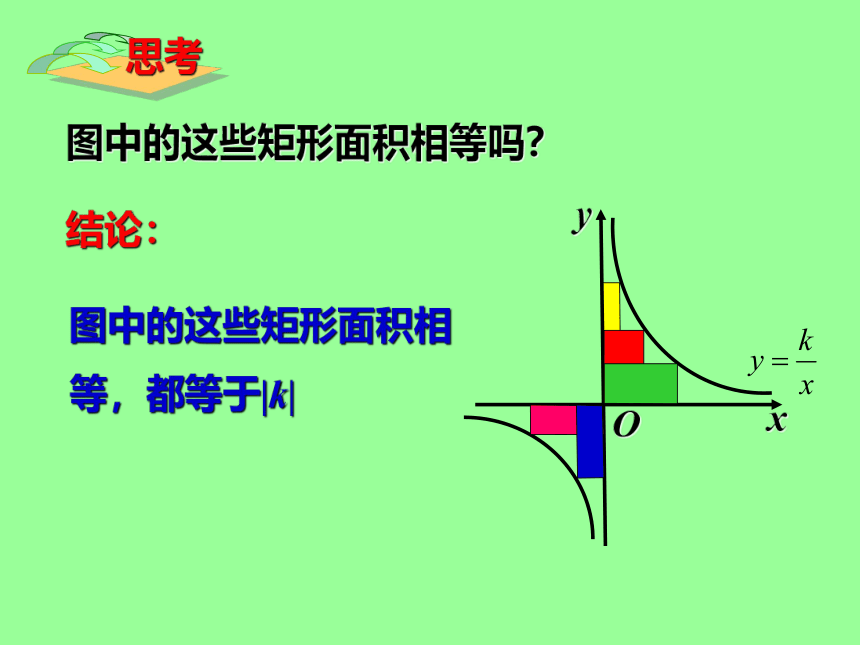
图中的这些矩形面积相等,都等于|k|
结论:
图中的这些矩形面积相等吗?
思考
P(m,n)
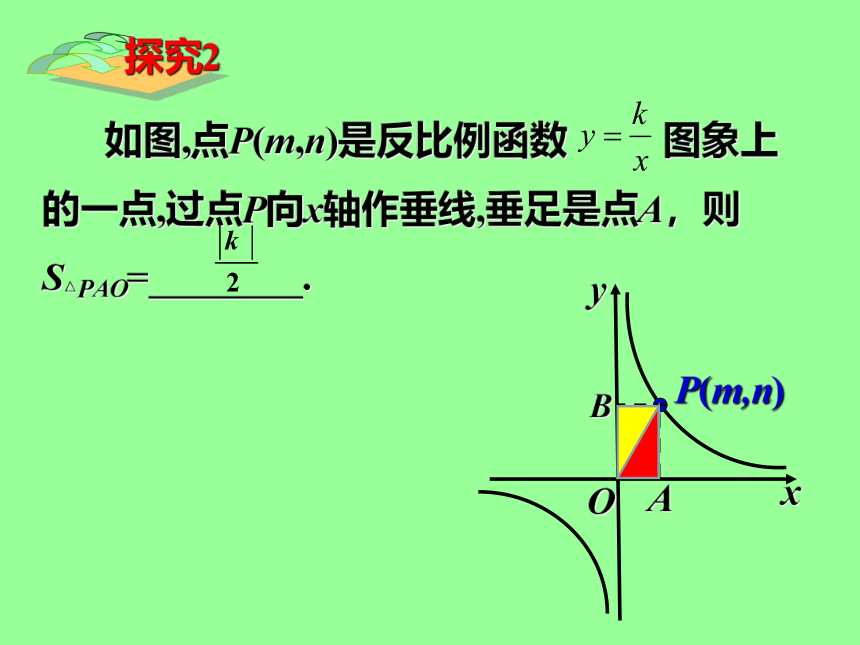
如图,点P(m,n)是反比例函数 图象上的一点,过点P向x轴作垂线,垂足是点A,则S△PAO=________.
x
y
O
A
探究2
B
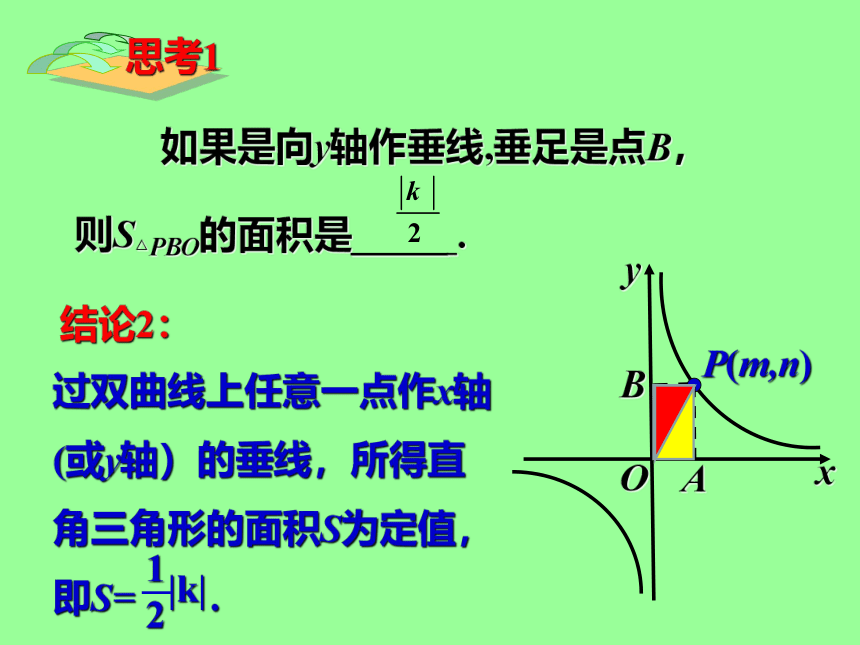
如果是向y轴作垂线,垂足是点B,
则S△PBO的面积是_____ .
x
y
O
B
思考1
结论2:
过双曲线上任意一点作x轴(或y轴)的垂线,所得直角三角形的面积S为定值,即S= .
|k|
1
2
P(m,n)
A
x
y
O
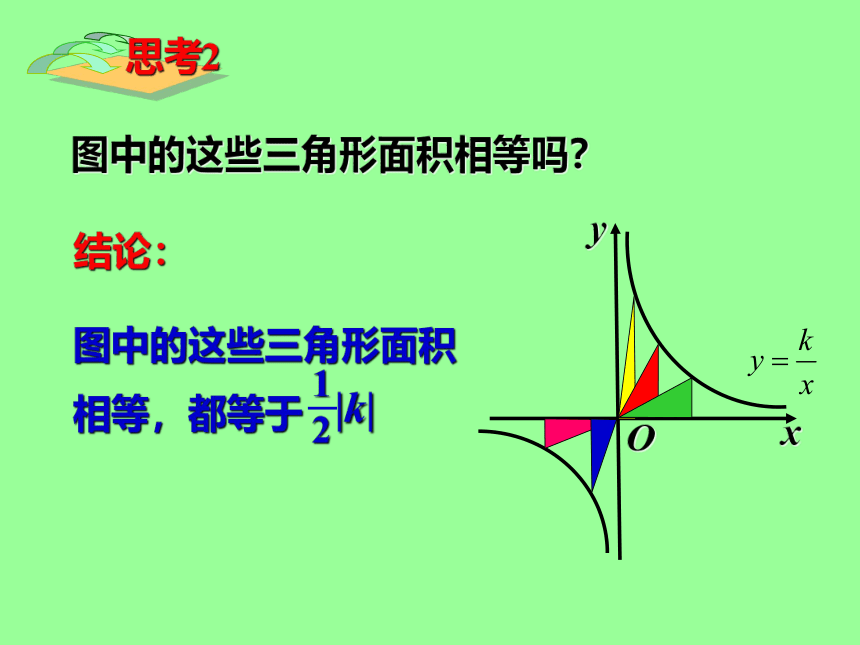
图中的这些三角形面积相等,都等于
结论:
图中的这些三角形面积相等吗?
|k|
1
2
思考2
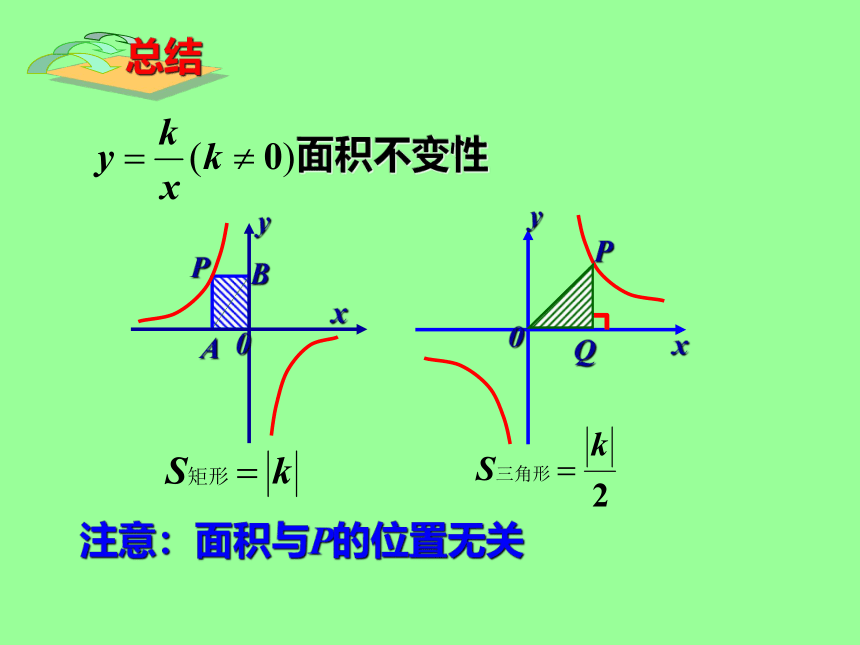
面积不变性
注意:面积与P的位置无关
Q
P
0
x
y
P
0
x
y
A
B
总结
1.如图,点P是反比例函数 图象上的一点,过点P分别向x轴、y轴作垂线,则阴影部分面积为_____.
x
y
O
M
N
P
练习
由解析式 求图形的面积
y=-
3
x
3
2.如图,点A、B是双曲线 上的点,过点A、B两点分别向x轴、y轴作垂线,若S阴影=1,则S1+S2= ________.
x
y
A
B
O
4
练习
由解析式求图形的面积
2
2
变式:如图,过反比例函数 图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,⊿AOE与梯形ECDB的面积分别为 S1 、S2,比较它们的大小,可得 ( )
A.S1>S2 B.S1=S2
C.S1< S2 D.S1和S2的大小关系不确定
B
练习
由解析式求图形的面积
3.如图,点P是反比例函数 图象上
的一点,PD⊥x轴于D.则△POD的面积为____.
P
D
o
y
x
1
练习
由解析式 求图形的面积
P
D
O
y
x
4.如图,点P是反比例函数图象上的一点,且PD⊥x轴于D.如果△POD面积为3,则这个反比例函数的解析式为________.
练习
y =
6
x
由图形的面积求解析式
P
D
O
y
x
一变: 点P是反比例函数图象上的一点,且PD⊥x轴于D.如果△POD面积为3,则这个反比例函数的解析式为_________________.
练习
由图形的面积求解析式
如图,
y =
6
x
或y =-
6
x
分类讨论
二变:如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为3,则这个反比例函数的解析式为 .
y=
6
x
练习
由图形的面积求解析式
O
A
x
y
B
P
同底等高的两个三角形的面积相等.
三变:如图,已知点A在反比例函数的图象上,AB⊥x轴于点B,点C为y轴上的一点,若△ABC的面积是3,则反比例函数的解析式为______.
O
A
x
y
B
C
y=
6
x
练习
由图形的面积求解析式
挑战训练
1.双曲线 和y2在第一象限的图像如图,过
y1上的任意一点A作x轴的平行线交y2于B ,交y轴于C,若S△AOB=1,则y2的解析式是_______.
y=
6
x
2
3
B
A
O
y
x
2.双曲线 在x轴上方的图象如图所示,作一条平行于 x 轴的直线分别交双曲线
于A、B 两点,连接OA、OB,则△AOB 的面积为 .
1.5
挑战训练
3.在双曲线 上任一点分别作x轴、y轴的垂线段,与x轴y轴围成矩形面积为12,则函数解析式为______________.
(x>0)
y
x
O
挑战训练
O
4.如图,A在双曲线 上,点B在双曲线
上,且AB∥x轴,C、D在x 轴上,若四边形
ABCD为矩形,则它的面积为 .
E
2
挑战训练
挑战训练
5.如图,双曲线 (x>0)的图象经过矩形OABC对角线的交点D,则矩形OABC的面积为———— 。
8
E
F
挑战训练
6.如图,已知双曲线 (x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k=_____.
2
如图,正比例函数 与反比例函数 的图象相交于A、C两点,过A点作x轴的垂线交x轴于B,连结BC则 面积S为多少?
拓展训练
如图,正比例函数 与反比例函数 的图象相交于A、C两点,过A点作x轴的垂线交x轴于B,连结BC,则 面积S为多少?
D
讲解
解:因为点A与点C关于原点中心对称,
设A(x,y),则C(-x,-y),过C点做CD ⊥x轴,垂足为D.
综合探究
反比例函数 与一次函数y=kx+b交于点A(1,8 ) 和B (4,n),
求:⑴这两个函数的解析式;
⑵三角形⊿AOB的面积。
y
x
x
o
o
A
B
o
o
——与面积有关的问题
学习目标
知识目标:掌握利用反比例函数解析式中比例系数解决矩形,三角形面积问题。
能力目标:培养自己自主探究,合作交流 的能力。
情感态度:通过讨论交流,合作学习,培养自己研究问题,解决问题的能力。
P(m,n)
如图,点P(m,n)是反比例函数 图象上的一点,过点P分别向x轴、y轴作垂线,垂足分别是点A、B,则S矩形OAPB=________.
x
y
O
A
B
过双曲线上任意一点作x轴、y轴的垂线,所得矩形的面积S为定值,即S=|k|.
探究1
结论1:
|k|
x
y
O
图中的这些矩形面积相等,都等于|k|
结论:
图中的这些矩形面积相等吗?
思考
P(m,n)
如图,点P(m,n)是反比例函数 图象上的一点,过点P向x轴作垂线,垂足是点A,则S△PAO=________.
x
y
O
A
探究2
B
如果是向y轴作垂线,垂足是点B,
则S△PBO的面积是_____ .
x
y
O
B
思考1
结论2:
过双曲线上任意一点作x轴(或y轴)的垂线,所得直角三角形的面积S为定值,即S= .
|k|
1
2
P(m,n)
A
x
y
O
图中的这些三角形面积相等,都等于
结论:
图中的这些三角形面积相等吗?
|k|
1
2
思考2
面积不变性
注意:面积与P的位置无关
Q
P
0
x
y
P
0
x
y
A
B
总结
1.如图,点P是反比例函数 图象上的一点,过点P分别向x轴、y轴作垂线,则阴影部分面积为_____.
x
y
O
M
N
P
练习
由解析式 求图形的面积
y=-
3
x
3
2.如图,点A、B是双曲线 上的点,过点A、B两点分别向x轴、y轴作垂线,若S阴影=1,则S1+S2= ________.
x
y
A
B
O
4
练习
由解析式求图形的面积
2
2
变式:如图,过反比例函数 图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,⊿AOE与梯形ECDB的面积分别为 S1 、S2,比较它们的大小,可得 ( )
A.S1>S2 B.S1=S2
C.S1< S2 D.S1和S2的大小关系不确定
B
练习
由解析式求图形的面积
3.如图,点P是反比例函数 图象上
的一点,PD⊥x轴于D.则△POD的面积为____.
P
D
o
y
x
1
练习
由解析式 求图形的面积
P
D
O
y
x
4.如图,点P是反比例函数图象上的一点,且PD⊥x轴于D.如果△POD面积为3,则这个反比例函数的解析式为________.
练习
y =
6
x
由图形的面积求解析式
P
D
O
y
x
一变: 点P是反比例函数图象上的一点,且PD⊥x轴于D.如果△POD面积为3,则这个反比例函数的解析式为_________________.
练习
由图形的面积求解析式
如图,
y =
6
x
或y =-
6
x
分类讨论
二变:如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为3,则这个反比例函数的解析式为 .
y=
6
x
练习
由图形的面积求解析式
O
A
x
y
B
P
同底等高的两个三角形的面积相等.
三变:如图,已知点A在反比例函数的图象上,AB⊥x轴于点B,点C为y轴上的一点,若△ABC的面积是3,则反比例函数的解析式为______.
O
A
x
y
B
C
y=
6
x
练习
由图形的面积求解析式
挑战训练
1.双曲线 和y2在第一象限的图像如图,过
y1上的任意一点A作x轴的平行线交y2于B ,交y轴于C,若S△AOB=1,则y2的解析式是_______.
y=
6
x
2
3
B
A
O
y
x
2.双曲线 在x轴上方的图象如图所示,作一条平行于 x 轴的直线分别交双曲线
于A、B 两点,连接OA、OB,则△AOB 的面积为 .
1.5
挑战训练
3.在双曲线 上任一点分别作x轴、y轴的垂线段,与x轴y轴围成矩形面积为12,则函数解析式为______________.
(x>0)
y
x
O
挑战训练
O
4.如图,A在双曲线 上,点B在双曲线
上,且AB∥x轴,C、D在x 轴上,若四边形
ABCD为矩形,则它的面积为 .
E
2
挑战训练
挑战训练
5.如图,双曲线 (x>0)的图象经过矩形OABC对角线的交点D,则矩形OABC的面积为———— 。
8
E
F
挑战训练
6.如图,已知双曲线 (x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k=_____.
2
如图,正比例函数 与反比例函数 的图象相交于A、C两点,过A点作x轴的垂线交x轴于B,连结BC则 面积S为多少?
拓展训练
如图,正比例函数 与反比例函数 的图象相交于A、C两点,过A点作x轴的垂线交x轴于B,连结BC,则 面积S为多少?
D
讲解
解:因为点A与点C关于原点中心对称,
设A(x,y),则C(-x,-y),过C点做CD ⊥x轴,垂足为D.
综合探究
反比例函数 与一次函数y=kx+b交于点A(1,8 ) 和B (4,n),
求:⑴这两个函数的解析式;
⑵三角形⊿AOB的面积。
y
x
x
o
o
A
B
o
o
