华东师大版 八年级下册课件:18.1_平行四边形的性质(共28张PPT)
文档属性
| 名称 | 华东师大版 八年级下册课件:18.1_平行四边形的性质(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 09:47:39 | ||
图片预览





文档简介
平行四边形的性质
数学华师大版 八年级下
新知导入
生活中的平行四边形
新知讲解
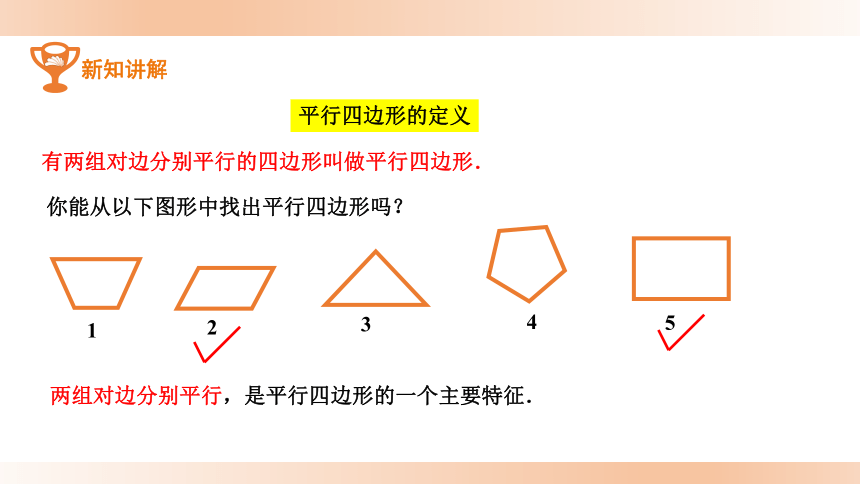
有两组对边分别平行的四边形叫做平行四边形.
平行四边形的定义
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征.
2
3
1
4
5
新知讲解
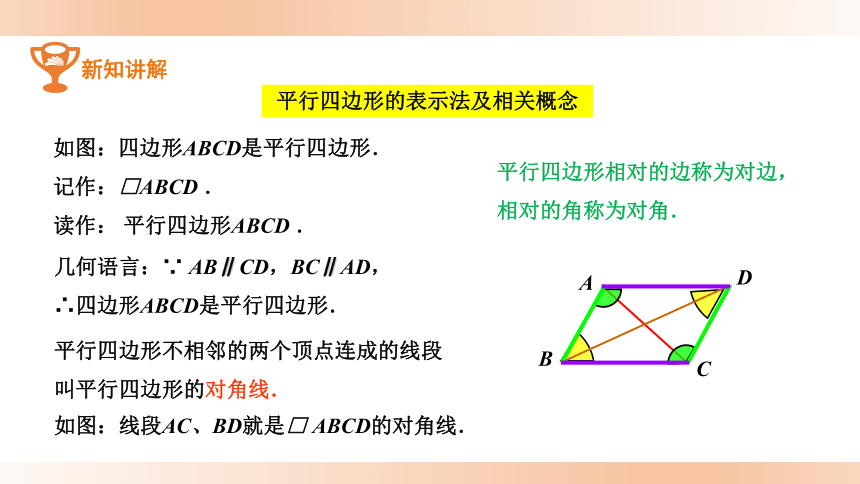
平行四边形相对的边称为对边,相对的角称为对角.
如图:线段AC、BD就是□ ABCD的对角线.
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
如图:四边形ABCD是平行四边形.
记作:□ABCD .
读作: 平行四边形ABCD .
几何语言:∵ AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形.
平行四边形的表示法及相关概念
新知讲解
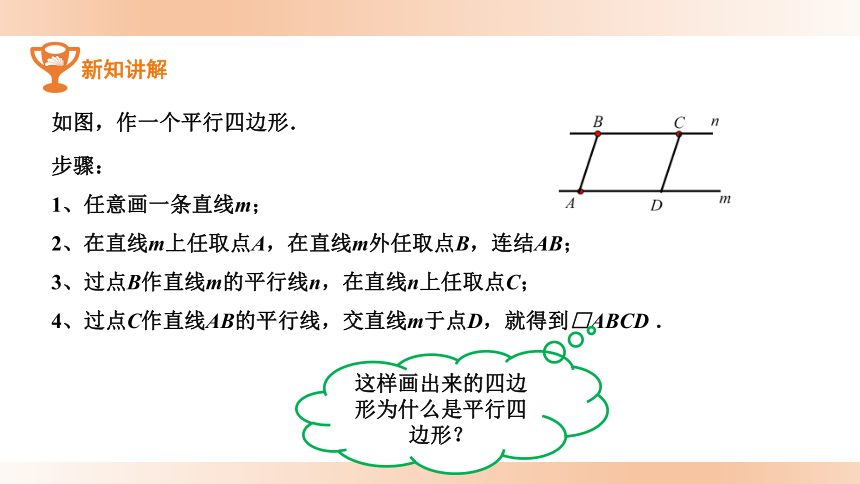
如图,作一个平行四边形.
步骤:
1、任意画一条直线m;
2、在直线m上任取点A,在直线m外任取点B,连结AB;
3、过点B作直线m的平行线n,在直线n上任取点C;
4、过点C作直线AB的平行线,交直线m于点D,就得到□ABCD .
这样画出来的四边形为什么是平行四边形?
新知讲解
在□ABCD 中,连结AC、BD,它们的交点记为点O.将□ABCD绕点O旋转180° .观察旋转后的□ABCD与原图形是否重合?由此你能得到什么结论?
你还能从中得出□ABCD的一些边角关系吗?
旋转后的□ABCD与原图形重合,所以平行四边形是中心对称图形,对角线的交点O就是对称中心.
AB=CD,BC=AD,∠A=∠C,∠B=∠D.
新知讲解
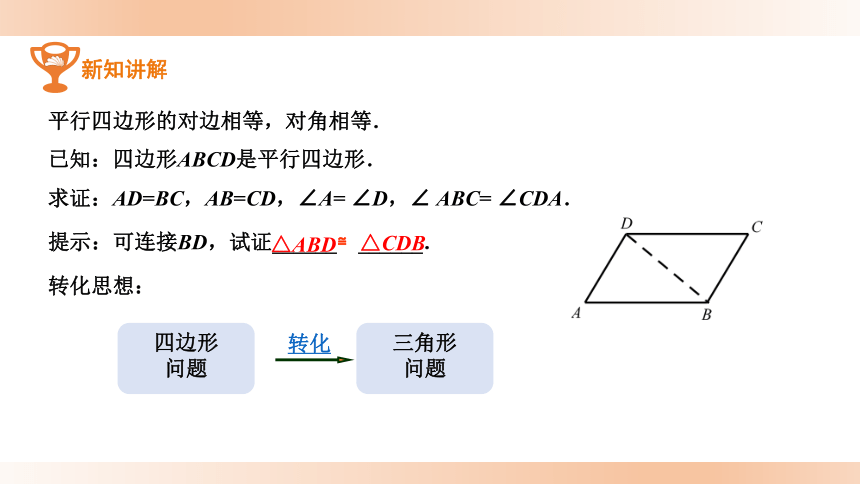
平行四边形的对边相等,对角相等.
已知:四边形ABCD是平行四边形.
求证:AD=BC,AB=CD,∠A= ∠D,∠ ABC= ∠CDA.
提示:可连接BD,试证______≌______.
转化思想:
四边形
问题
三角形
问题
转化
△ABD
△CDB
新知讲解
已知 :□ABCD(如图).
求证:AB=CD,BC=DA;∠B=∠D,∠ABC=∠CDA.
即∠ABC=∠CDA.
证明:连结BD.
∵AB∥CD,AD∥BC(平行四边形的对边平行),
∴∠1=∠2,∠3=∠4,
∴AB=CD,BC=DA,∠A=∠C.
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3.
∴△ABD≌△CDB.
在△ABD和△DCE中,
∵ ,
新知讲解
平行四边形的性质定理1 平行四边形的对边相等.
平行四边形的性质定理2 平行四边形的对角相等.
2、平行四边形的对边相等.平行四边形的对边平行.
1、平行四边形是中心对称图形.
平行四边形的性质
3、平行四边形的对角相等.平行四边形的邻角互补.
新知讲解
例1 在□ABCD中,∠A=40 °,求其他各内角的大小.
解:在□ABCD中, ∠A=∠C,∠B=∠D(平行四边形的对角相等).
∵ ∠A=40°(已知),
∴ ∠C=40°.
又∵AD∥BC(平行四边形的对边平行),
∴∠A+∠B=180°(两直线平行,同旁内角互补).
∴∠B= 180 -∠A= 180?- 40°=140 °,
∠D= ∠B= 140 °.
新知讲解
例2 如图,在□ABCD中,AB=8,周长等于24.求其余三条边的长.
解: 在□ ABCD中,
AB=DC,AD=BC(平行四边形的对边相等).
∵AB=8,
∴DC=8,
又∵AB+BC+DC+AD=24,
∴ AD=BC= .
新知讲解
在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺量出平行线之间这些垂线段的长度.你能发现什么结论?试用平行四边形的性质定理加以说明.
两条直线平行,其中一条直线上的任一点到另一条直线的距离,叫做这两条平行线之间的距离.
平行线之间的距离处处相等.
新知讲解
例3 已知平行四边形的周长是24,相邻两边的长度相差4,求该平行四边形相邻两边的长.
解:设AB的长为x,则BC的长为x+4.
根据已知,可得,
2(AB + BC)=24,即2(x +x +4)=24
4 x +8 =24,
解得x=4 .
所以,该平行四边形相邻两边的长分别为4和8 .
新知讲解
例4 已知:如图,在□ABCD中,∠ADC的平分线与AB相交于点E.求证:BE+BC=CD.
证明:∵四边形ABCD是平行四边形,
∴AB=CD(平行四边形的对边相等),
AB∥CD(平行四边形的对边平行),
∴∠CDE=∠AED.
又∵DE是∠ADC的平分线,
∴∠ADE=∠CDE, ∠ADE=∠AED,
∴AD=AE.
又∵AD=BC (平行四边形的对边相等),
∴ AE=BC.
BE+BC= BE+AE= CD.
新知讲解
A
D
B
C
如图□ ABCD 的两条对角线AC、BD相交于点O.
(1)图中有哪些三角形是全等的?
有哪些线段是相等的?
(2)能设法验证你的结论吗?
你可以用测量的方法,也可以用复制纸片并借助旋转的方法.
A
D
B
C
o
新知讲解
由上题你又能得出平行四边形怎样的性质?
如图□ ABCD 的两条对角线AC、BD相交于点O.
几何语言:
定理3 平行四边形的对角线互相平分.
新知讲解
已知:如图,□ ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
证明:∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
分析:要证明相等的OA与OC、OB与OD分别属于△AOB与△COD,因此只需证明这两个三角形全等即可.
新知讲解
例5 如图,□ ABCD的对角线AC和 BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC与BD的和是多少?
解:在□ ABCD中
∵∴AB=6,AO+BO+AB=15,
∴AO+BO=15-6=9.
又∵AO=OC,BO=OD(平行四边形对角线互相平分),
∴AC+BD=2AO+2BO=2(AO+BO)=9×2=18.
新知讲解
例6 如图,□ ABCD的对角线AC和BD相交于点O,EF过点O且与AB,CD相交于点E和点F.求证:OE=OF.
解:∵ABCD是平行四边形,
∴OB=OD(平行四边形对角线互相平分).
又∵AB∥CD,
∴∠EBO=∠FDO.
又∵ ∠EBO=∠DOF,
∴△BEO≌△DFO.
∴OE=OF.
分析:要证明OE=OF,只要证明它们所在的两个三角形全等即可.
新知讲解
例7 如图,□ ABCD的对角线AC与BD相交于点O,其周长为16,且△AOB的周长比△BOC的周长小2.求边AB和BC的长.
解:∵四边形ABCD是平行四边形,
∴OA=OC(平行四边形对角线互相平分).
∵ △AOB的周+2= △BOC的周长,
∴AO+BO+AB+2=BO+CO+BC,
即 AB+2=BC.
又∵ □ ABCD的周长=16,
∴2(AB+BC)=16,
即4AB+4=16.
∴AB=3,BC=5.
新知讲解
例8 如图,在□ ABCD中,对角线AC=21cm,BE⊥AC,垂足为E ,且BE=5cm,AD=7cm.求AD和BC之间的距离.
解:设AD和BC之间的距离为x cm ,
则□ ABCD的面积等于AD·x.
∴AD·x=AC·BE,
即7x=21×5,
x=15(cm),
即AD和BC之间的距离为15cm.
课堂练习
1.在□ABCD中,∠A=65°,则∠B= °,∠C= °,∠D= °.
2.在□ABCD中,AB+CD=28cm.□ABCD的周长等于96cm, 则AB= ,BC= , CD= , AD= .
115
65
115
14cm
34cm
14cm
34cm
3.已知: □ ABCD的对角线AC、BD相交于点O,AC =16cm,BD =12cm,BC =10cm,则□ABCD 的周长是_______,□ ABCD的面积是__________ .
40cm
96cm2
5.平行四边形的一边长为5cm,则它的对角线可能是( )
A、4cm和6cm B、4cm和14cm C、4cm和8cm D、12cm和2 cm
4 .在□ ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1 C.1:1:2:2 D.2:1:2:1
D
C
课堂练习
6.在□ABCD中,∠A=3∠B,求∠C和∠D的度数 .
解: ∵在□ABCD中,AD∥BC,
∴∠A+∠B= 180°.
又已知 ∠A=3∠B,
则 3∠B +∠B= 180°.
解得:∠B= 45°,∠A=3×45°=135 °,
所以 ∠C=∠A=135 °,∠D=∠B= 45°.
拓展提高
7.如图?ABCD中,AC、BD交于O点,点E、F分别是AO、CO的中点,试判断线段BE、DF的关系并证明你的结论.
解:BE=DF,BE∥DF.
证明:∵ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F分别是OA,OC的中点,
∴OE=OF,
又∵∠BOE=∠DOF,
∴△BOE≌△DOF,
∴BE=DF,∠OEB=∠OFD,
∴BE∥DF.
中考链接
1、【2018?贵州】如图,在□ABCD中,已知AC=4 cm,若△ACD的周长为13 cm,则□ABCD的周长为( )
A.26 cm B.24 cm C.20 cm D.18 cm
2、【2018?江苏】如图,在□ABCD中,∠A =70°,DC = DB ,则∠CDB =_________ .
3、【2018?湖北】如图,已知□ABCD的对角线AC、BD交于点O,且AC=8,
BD=10,AB=5,则△OCD的周长为_________ .
D
40°
14
课堂总结
1、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
2、平行四边形的表示方法:平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD” .
3、平行四边形的性质:
(1)平行四边形是中心对称图形.
(2)平行四边形的对边相等.平行四边形的对边平行.
(3)平行四边形的对角相等.平行四边形的邻角互补.
(4)平行四边形的对角线互相平分.
板书设计
平行四边形的定义:
平行四边形的表示方法:
平行四边形的性质:
边:两组对边分别平行,两组对边分别相等.
角:对角相等,邻角互补.
对角线:互相平分.
对称性:中心对称图形.
平行线之间的距离处处相等.
例题
作业布置
教材第80页,第1、2、4、6题.
数学华师大版 八年级下
新知导入
生活中的平行四边形
新知讲解
有两组对边分别平行的四边形叫做平行四边形.
平行四边形的定义
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征.
2
3
1
4
5
新知讲解
平行四边形相对的边称为对边,相对的角称为对角.
如图:线段AC、BD就是□ ABCD的对角线.
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
如图:四边形ABCD是平行四边形.
记作:□ABCD .
读作: 平行四边形ABCD .
几何语言:∵ AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形.
平行四边形的表示法及相关概念
新知讲解
如图,作一个平行四边形.
步骤:
1、任意画一条直线m;
2、在直线m上任取点A,在直线m外任取点B,连结AB;
3、过点B作直线m的平行线n,在直线n上任取点C;
4、过点C作直线AB的平行线,交直线m于点D,就得到□ABCD .
这样画出来的四边形为什么是平行四边形?
新知讲解
在□ABCD 中,连结AC、BD,它们的交点记为点O.将□ABCD绕点O旋转180° .观察旋转后的□ABCD与原图形是否重合?由此你能得到什么结论?
你还能从中得出□ABCD的一些边角关系吗?
旋转后的□ABCD与原图形重合,所以平行四边形是中心对称图形,对角线的交点O就是对称中心.
AB=CD,BC=AD,∠A=∠C,∠B=∠D.
新知讲解
平行四边形的对边相等,对角相等.
已知:四边形ABCD是平行四边形.
求证:AD=BC,AB=CD,∠A= ∠D,∠ ABC= ∠CDA.
提示:可连接BD,试证______≌______.
转化思想:
四边形
问题
三角形
问题
转化
△ABD
△CDB
新知讲解
已知 :□ABCD(如图).
求证:AB=CD,BC=DA;∠B=∠D,∠ABC=∠CDA.
即∠ABC=∠CDA.
证明:连结BD.
∵AB∥CD,AD∥BC(平行四边形的对边平行),
∴∠1=∠2,∠3=∠4,
∴AB=CD,BC=DA,∠A=∠C.
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3.
∴△ABD≌△CDB.
在△ABD和△DCE中,
∵ ,
新知讲解
平行四边形的性质定理1 平行四边形的对边相等.
平行四边形的性质定理2 平行四边形的对角相等.
2、平行四边形的对边相等.平行四边形的对边平行.
1、平行四边形是中心对称图形.
平行四边形的性质
3、平行四边形的对角相等.平行四边形的邻角互补.
新知讲解
例1 在□ABCD中,∠A=40 °,求其他各内角的大小.
解:在□ABCD中, ∠A=∠C,∠B=∠D(平行四边形的对角相等).
∵ ∠A=40°(已知),
∴ ∠C=40°.
又∵AD∥BC(平行四边形的对边平行),
∴∠A+∠B=180°(两直线平行,同旁内角互补).
∴∠B= 180 -∠A= 180?- 40°=140 °,
∠D= ∠B= 140 °.
新知讲解
例2 如图,在□ABCD中,AB=8,周长等于24.求其余三条边的长.
解: 在□ ABCD中,
AB=DC,AD=BC(平行四边形的对边相等).
∵AB=8,
∴DC=8,
又∵AB+BC+DC+AD=24,
∴ AD=BC= .
新知讲解
在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺量出平行线之间这些垂线段的长度.你能发现什么结论?试用平行四边形的性质定理加以说明.
两条直线平行,其中一条直线上的任一点到另一条直线的距离,叫做这两条平行线之间的距离.
平行线之间的距离处处相等.
新知讲解
例3 已知平行四边形的周长是24,相邻两边的长度相差4,求该平行四边形相邻两边的长.
解:设AB的长为x,则BC的长为x+4.
根据已知,可得,
2(AB + BC)=24,即2(x +x +4)=24
4 x +8 =24,
解得x=4 .
所以,该平行四边形相邻两边的长分别为4和8 .
新知讲解
例4 已知:如图,在□ABCD中,∠ADC的平分线与AB相交于点E.求证:BE+BC=CD.
证明:∵四边形ABCD是平行四边形,
∴AB=CD(平行四边形的对边相等),
AB∥CD(平行四边形的对边平行),
∴∠CDE=∠AED.
又∵DE是∠ADC的平分线,
∴∠ADE=∠CDE, ∠ADE=∠AED,
∴AD=AE.
又∵AD=BC (平行四边形的对边相等),
∴ AE=BC.
BE+BC= BE+AE= CD.
新知讲解
A
D
B
C
如图□ ABCD 的两条对角线AC、BD相交于点O.
(1)图中有哪些三角形是全等的?
有哪些线段是相等的?
(2)能设法验证你的结论吗?
你可以用测量的方法,也可以用复制纸片并借助旋转的方法.
A
D
B
C
o
新知讲解
由上题你又能得出平行四边形怎样的性质?
如图□ ABCD 的两条对角线AC、BD相交于点O.
几何语言:
定理3 平行四边形的对角线互相平分.
新知讲解
已知:如图,□ ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
证明:∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
分析:要证明相等的OA与OC、OB与OD分别属于△AOB与△COD,因此只需证明这两个三角形全等即可.
新知讲解
例5 如图,□ ABCD的对角线AC和 BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC与BD的和是多少?
解:在□ ABCD中
∵∴AB=6,AO+BO+AB=15,
∴AO+BO=15-6=9.
又∵AO=OC,BO=OD(平行四边形对角线互相平分),
∴AC+BD=2AO+2BO=2(AO+BO)=9×2=18.
新知讲解
例6 如图,□ ABCD的对角线AC和BD相交于点O,EF过点O且与AB,CD相交于点E和点F.求证:OE=OF.
解:∵ABCD是平行四边形,
∴OB=OD(平行四边形对角线互相平分).
又∵AB∥CD,
∴∠EBO=∠FDO.
又∵ ∠EBO=∠DOF,
∴△BEO≌△DFO.
∴OE=OF.
分析:要证明OE=OF,只要证明它们所在的两个三角形全等即可.
新知讲解
例7 如图,□ ABCD的对角线AC与BD相交于点O,其周长为16,且△AOB的周长比△BOC的周长小2.求边AB和BC的长.
解:∵四边形ABCD是平行四边形,
∴OA=OC(平行四边形对角线互相平分).
∵ △AOB的周+2= △BOC的周长,
∴AO+BO+AB+2=BO+CO+BC,
即 AB+2=BC.
又∵ □ ABCD的周长=16,
∴2(AB+BC)=16,
即4AB+4=16.
∴AB=3,BC=5.
新知讲解
例8 如图,在□ ABCD中,对角线AC=21cm,BE⊥AC,垂足为E ,且BE=5cm,AD=7cm.求AD和BC之间的距离.
解:设AD和BC之间的距离为x cm ,
则□ ABCD的面积等于AD·x.
∴AD·x=AC·BE,
即7x=21×5,
x=15(cm),
即AD和BC之间的距离为15cm.
课堂练习
1.在□ABCD中,∠A=65°,则∠B= °,∠C= °,∠D= °.
2.在□ABCD中,AB+CD=28cm.□ABCD的周长等于96cm, 则AB= ,BC= , CD= , AD= .
115
65
115
14cm
34cm
14cm
34cm
3.已知: □ ABCD的对角线AC、BD相交于点O,AC =16cm,BD =12cm,BC =10cm,则□ABCD 的周长是_______,□ ABCD的面积是__________ .
40cm
96cm2
5.平行四边形的一边长为5cm,则它的对角线可能是( )
A、4cm和6cm B、4cm和14cm C、4cm和8cm D、12cm和2 cm
4 .在□ ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1 C.1:1:2:2 D.2:1:2:1
D
C
课堂练习
6.在□ABCD中,∠A=3∠B,求∠C和∠D的度数 .
解: ∵在□ABCD中,AD∥BC,
∴∠A+∠B= 180°.
又已知 ∠A=3∠B,
则 3∠B +∠B= 180°.
解得:∠B= 45°,∠A=3×45°=135 °,
所以 ∠C=∠A=135 °,∠D=∠B= 45°.
拓展提高
7.如图?ABCD中,AC、BD交于O点,点E、F分别是AO、CO的中点,试判断线段BE、DF的关系并证明你的结论.
解:BE=DF,BE∥DF.
证明:∵ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F分别是OA,OC的中点,
∴OE=OF,
又∵∠BOE=∠DOF,
∴△BOE≌△DOF,
∴BE=DF,∠OEB=∠OFD,
∴BE∥DF.
中考链接
1、【2018?贵州】如图,在□ABCD中,已知AC=4 cm,若△ACD的周长为13 cm,则□ABCD的周长为( )
A.26 cm B.24 cm C.20 cm D.18 cm
2、【2018?江苏】如图,在□ABCD中,∠A =70°,DC = DB ,则∠CDB =_________ .
3、【2018?湖北】如图,已知□ABCD的对角线AC、BD交于点O,且AC=8,
BD=10,AB=5,则△OCD的周长为_________ .
D
40°
14
课堂总结
1、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
2、平行四边形的表示方法:平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD” .
3、平行四边形的性质:
(1)平行四边形是中心对称图形.
(2)平行四边形的对边相等.平行四边形的对边平行.
(3)平行四边形的对角相等.平行四边形的邻角互补.
(4)平行四边形的对角线互相平分.
板书设计
平行四边形的定义:
平行四边形的表示方法:
平行四边形的性质:
边:两组对边分别平行,两组对边分别相等.
角:对角相等,邻角互补.
对角线:互相平分.
对称性:中心对称图形.
平行线之间的距离处处相等.
例题
作业布置
教材第80页,第1、2、4、6题.
