华东师大版 八年级下册课件:19.3 正方形(共19张PPT)
文档属性
| 名称 | 华东师大版 八年级下册课件:19.3 正方形(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 09:48:54 | ||
图片预览




文档简介
正 方 形
数学华师大版 八年级下
新知导入
把一张矩形纸片如图那样折一下,就可以裁出什么形状的纸片?
正方形具有什么性质?
正方形
新知讲解
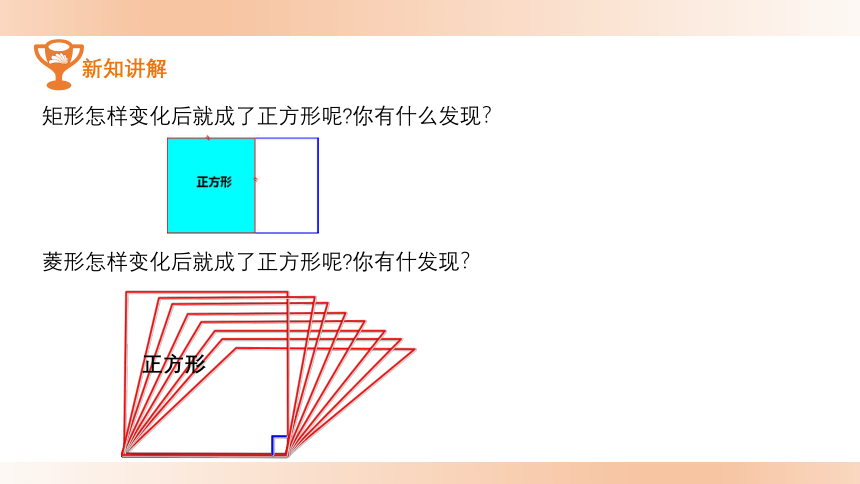
矩形怎样变化后就成了正方形呢?你有什么发现?
菱形怎样变化后就成了正方形呢?你有什发现?
正方形
新知讲解
矩 形
〃
〃
正方形
邻边相等
〃
〃
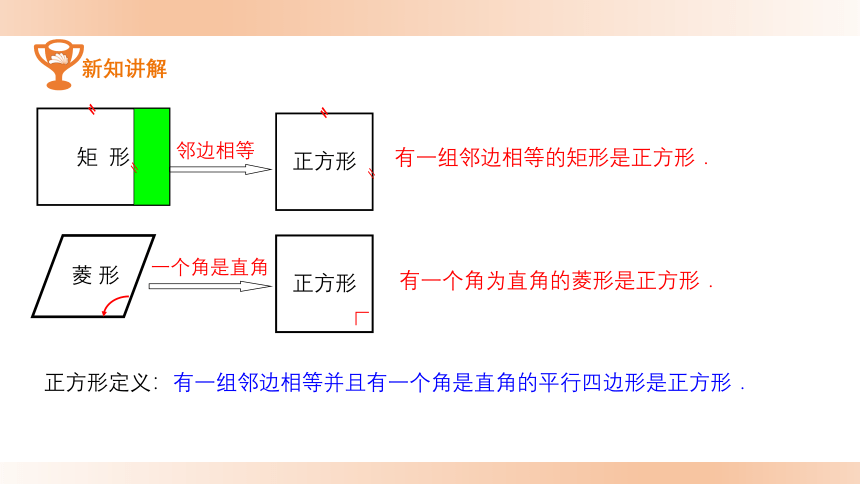
有一组邻边相等的矩形是正方形.
菱 形
一个角是直角
正方形
∟
有一个角为直角的菱形是正方形.
正方形定义:有一组邻边相等并且有一个角是直角的平行四边形是正方形.
新知讲解
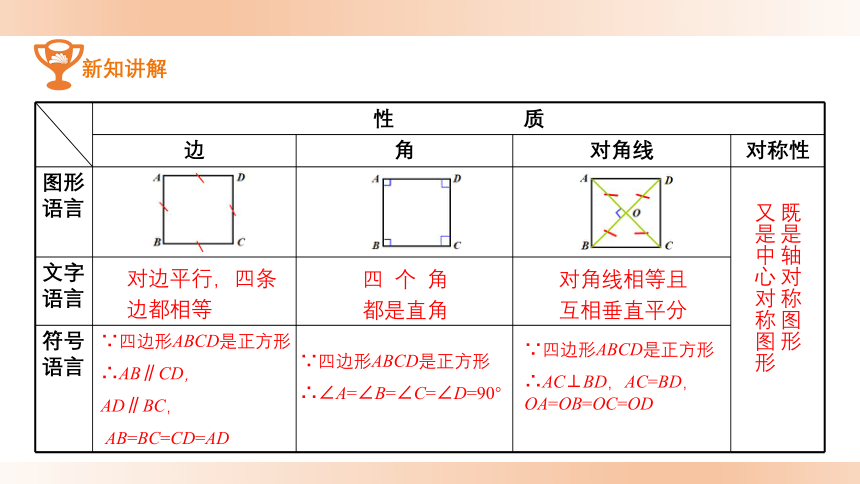
性 质
边
角
对角线
对称性
图形语言
文字语言
符号语言
对边平行,四条边都相等
四 个 角
都是直角
对角线相等且互相垂直平分
∵四边形ABCD是正方形
∴AB∥CD,
AD∥BC,
AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
既是轴对称图形
又是中心对称图形
新知讲解
已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
证明:∵四边形ABCD是正方形.
∴∠A=90°,AB=AC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
正方形的四边相等,四个角都是直角.
正方形的四边相等,四个角都是直角.
新知讲解
例1 如图,已知正方ABCD.求∠ABD、∠DAC、∠DOC的度数.
分析:由正方形的特殊性质,可知∠DOC=90°.易证△ABO≌△CBO,
从而可得∠ABD= × 90°=45°,同理可得∠DAC= 45° .
解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OB=OC=OD,
∴ ∠DOC=90°.
∵ ∠AOB=∠COD= 90°,
∴ △ABO≌△CBO,从而可得∠ABD= × 90°=45°,
同理可得∠DAC= 45° .
新知讲解
正方形的判定方法:
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
新知讲解
讨论:下面三名同学的说法正确吗?请说出你的理由.
我是这样检验的:比较边的长度,发现四条边是相等的,所以我剪出的四边形是正方形.
我发现对角线相等,所以我剪出的四边形是正方形.
我比较了由对角线相互分成的4条线段,发现它们是相等的.所以我剪出的四边形是正方形.
新知讲解
矩形
菱形
正
方
形
平行四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.正方形既具有矩形的性质又具有菱形的性质.
平行四边形、矩形、菱形、正方形之间关系:
课堂练习
1. 下列判断中正确的是 ( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
2. 正方形具有而矩形不一定有的性质是 ( )
A.四个角是直角 B.对角线互相垂直
C.对角线互相平分 D.对角线相等
3. 矩形,菱形,正方形都具有的性质是 ( )
A.邻边相等 B. 邻角相等
C.对边相等 D. 对角互补
D
B
C
课堂练习
4、在正方形ABCD中,∠ADB= ,∠DAC= , ∠BOC= .
5、在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .
45°
90°
22.5°
45°
课堂练习
6、如图,分别延长等腰直角三角形OAB的两条直角边AO和BO,使AO=OC,BO=OD.求证:四边形ABCD是正方形.
证明:∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形
∵等腰三角形OAB中,
AO⊥BO,AO=BO,
∴AO=BO=CO=DO ,AC⊥BD 即 AC=BD.
∴四边形ABCD是正方形.
拓展提高
7、如图,在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF.BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且BE⊥DF.
理由如下:
∵四边形ABCD是正方形,
∴BC=DC,∠BCE =90° ,
∴∠DCF=180°-∠BCE=90°,
∴∠BCE=∠DCF.
又∵CE=CF,
∴△BCE≌△DCF.
∴BE=DF.
中考链接
【2018?浙江】如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90 ° ,
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60 ° ,
∵∠CEF=45 ° ,
∴∠CFE=∠CEF=45 ° ,
∴∠AFD=∠AEB=180 ° ?45 ° ?60 ° =75 ° ,
∴△AEB?△AFD(AAS) ,
∴AB=AD,∴矩形ABCD是正方形.
课堂总结
1. 正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形是正方形.
2. 正方形的性质:
正方形的对边平行,四条边都相等,四个角都是直角.
正方形的对角线相等,且互相垂直平分.
正方形是中心对称图形,对角线的交点是它的对称中心.
正方形是轴对称图形,两条对角线所在直线,以及过每一组对边中点的直线都是它的对称轴.
3. 正方形的判定:
有一组邻边相等的矩形是正方形;
有一个角是直角的菱形是正方形;
有一组邻边相等并且有一个角是直角的平行四边形是正方形.
课堂总结
5种判定方法
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
或每一条对角线 平分一组对角
板书设计
1、正方形的定义:
2、正方形的性质:
3、正方形的判定:
例1
作业布置
教材121页第1题、第2题、第3题.
数学华师大版 八年级下
新知导入
把一张矩形纸片如图那样折一下,就可以裁出什么形状的纸片?
正方形具有什么性质?
正方形
新知讲解
矩形怎样变化后就成了正方形呢?你有什么发现?
菱形怎样变化后就成了正方形呢?你有什发现?
正方形
新知讲解
矩 形
〃
〃
正方形
邻边相等
〃
〃
有一组邻边相等的矩形是正方形.
菱 形
一个角是直角
正方形
∟
有一个角为直角的菱形是正方形.
正方形定义:有一组邻边相等并且有一个角是直角的平行四边形是正方形.
新知讲解
性 质
边
角
对角线
对称性
图形语言
文字语言
符号语言
对边平行,四条边都相等
四 个 角
都是直角
对角线相等且互相垂直平分
∵四边形ABCD是正方形
∴AB∥CD,
AD∥BC,
AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
既是轴对称图形
又是中心对称图形
新知讲解
已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
证明:∵四边形ABCD是正方形.
∴∠A=90°,AB=AC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
正方形的四边相等,四个角都是直角.
正方形的四边相等,四个角都是直角.
新知讲解
例1 如图,已知正方ABCD.求∠ABD、∠DAC、∠DOC的度数.
分析:由正方形的特殊性质,可知∠DOC=90°.易证△ABO≌△CBO,
从而可得∠ABD= × 90°=45°,同理可得∠DAC= 45° .
解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OB=OC=OD,
∴ ∠DOC=90°.
∵ ∠AOB=∠COD= 90°,
∴ △ABO≌△CBO,从而可得∠ABD= × 90°=45°,
同理可得∠DAC= 45° .
新知讲解
正方形的判定方法:
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
新知讲解
讨论:下面三名同学的说法正确吗?请说出你的理由.
我是这样检验的:比较边的长度,发现四条边是相等的,所以我剪出的四边形是正方形.
我发现对角线相等,所以我剪出的四边形是正方形.
我比较了由对角线相互分成的4条线段,发现它们是相等的.所以我剪出的四边形是正方形.
新知讲解
矩形
菱形
正
方
形
平行四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.正方形既具有矩形的性质又具有菱形的性质.
平行四边形、矩形、菱形、正方形之间关系:
课堂练习
1. 下列判断中正确的是 ( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
2. 正方形具有而矩形不一定有的性质是 ( )
A.四个角是直角 B.对角线互相垂直
C.对角线互相平分 D.对角线相等
3. 矩形,菱形,正方形都具有的性质是 ( )
A.邻边相等 B. 邻角相等
C.对边相等 D. 对角互补
D
B
C
课堂练习
4、在正方形ABCD中,∠ADB= ,∠DAC= , ∠BOC= .
5、在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .
45°
90°
22.5°
45°
课堂练习
6、如图,分别延长等腰直角三角形OAB的两条直角边AO和BO,使AO=OC,BO=OD.求证:四边形ABCD是正方形.
证明:∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形
∵等腰三角形OAB中,
AO⊥BO,AO=BO,
∴AO=BO=CO=DO ,AC⊥BD 即 AC=BD.
∴四边形ABCD是正方形.
拓展提高
7、如图,在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF.BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且BE⊥DF.
理由如下:
∵四边形ABCD是正方形,
∴BC=DC,∠BCE =90° ,
∴∠DCF=180°-∠BCE=90°,
∴∠BCE=∠DCF.
又∵CE=CF,
∴△BCE≌△DCF.
∴BE=DF.
中考链接
【2018?浙江】如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90 ° ,
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60 ° ,
∵∠CEF=45 ° ,
∴∠CFE=∠CEF=45 ° ,
∴∠AFD=∠AEB=180 ° ?45 ° ?60 ° =75 ° ,
∴△AEB?△AFD(AAS) ,
∴AB=AD,∴矩形ABCD是正方形.
课堂总结
1. 正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形是正方形.
2. 正方形的性质:
正方形的对边平行,四条边都相等,四个角都是直角.
正方形的对角线相等,且互相垂直平分.
正方形是中心对称图形,对角线的交点是它的对称中心.
正方形是轴对称图形,两条对角线所在直线,以及过每一组对边中点的直线都是它的对称轴.
3. 正方形的判定:
有一组邻边相等的矩形是正方形;
有一个角是直角的菱形是正方形;
有一组邻边相等并且有一个角是直角的平行四边形是正方形.
课堂总结
5种判定方法
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
或每一条对角线 平分一组对角
板书设计
1、正方形的定义:
2、正方形的性质:
3、正方形的判定:
例1
作业布置
教材121页第1题、第2题、第3题.
