华东师大版八年级数学下册18.2 :平行四边形的判定 第一课时教学课件 (共19张PPT)
文档属性
| 名称 | 华东师大版八年级数学下册18.2 :平行四边形的判定 第一课时教学课件 (共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 09:51:33 | ||
图片预览





文档简介
科目:数学(华师版八年级下)
课题:平行四边形的判定
你怎么确定这四边形就是平行四边形呢?
爸爸,你看我做的平行四边形。
你还记得吗?
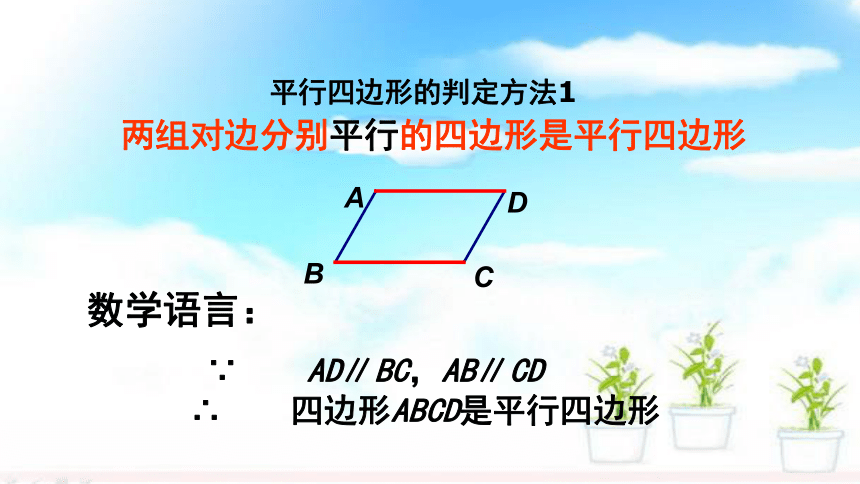
两组对边分别平行的四边形是平行四边形
平行四边形的定义
忆
平行四边形的主要性质:
3、对角线: 平行四边形对角线互相平分.
1、边 :
a.平行四边形两组对边分别平行.
b.平行四边形两组对边分别相等.
两组对边分别平行的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
(定义)
平行四边形的判定方法1
猜
说
你能分别说出它们的逆命题吗?
这些逆命题成立吗?
2、角:平行四边形的对角相等,邻角互补.
两组对边分别平行的四边形是平行四边形
∵ AD∥BC,AB∥CD
∴ 四边形ABCD是平行四边形
数学语言:
C
B
D
A
平行四边形的判定方法1
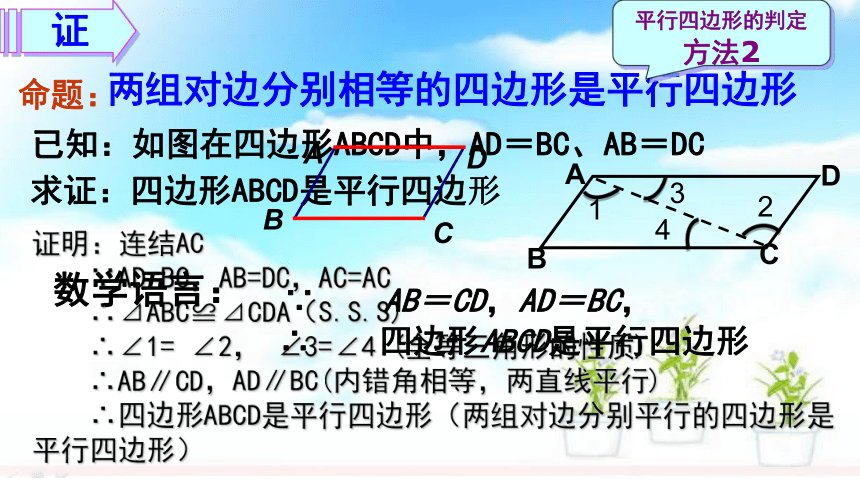
两组对边分别相等的四边形是平行四边形
已知:如图在四边形ABCD中,AD=BC、AB=DC
求证:四边形ABCD是平行四边形
A
C
D
1
3
2
4
B
证
证明:连结AC
∵AD=BC,AB=DC,AC=AC
∴⊿ABC≌⊿CDA(S.S.S)
∴∠1= ∠2, ∠3=∠4 (全等三角形的性质)
∴AB∥CD,AD∥BC(内错角相等,两直线平行)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是 平行四边形)
命题:
平行四边形的判定方法2
C
B
D
A
数学语言:
∵ AB=CD,AD=BC,
∴ 四边形ABCD是平行四边形
探
你还能想到其他的判定方法吗?
一组对边平行且相等的四边形是平行四边形
一组对边平行,另一组对边相等的四边形是平行四边形
已知:如图、在四边形ABCD中,AB∥CD、AB=CD
求证:四边形ABCD是平行四边形
A
C
D
1
3
2
4
B
一组对边平行且相等的四边形是平行四边形
命题:
? 探索1
? 探索1结论
∵ AB∥CD,AB=CD,
∴ 四边形ABCD是平行四边形
C
B
D
A
一组对边平行且相等的 四边形是平行四边形.
数学语言:
“平行且相等”常用符号“ ”来表示
AB∥CD且AB=CD,记作“AB CD”
∥
=
读作:“AB平行且相等于CD”
∥
=
平行四边形的判定方法3
一组对边平行,另一组对边相等的四边形是平行四边形
命题:
? 探索2
C
B
D
A
C
B
D
A
是假命题
2.两组对边分别相等的四边形是平行四边形.
平行四边形的判定方法:
1.两组对边分别平行的四边形是平行四边形.(定义)
3.一组对边平行且相等的四边形是平行四边形.
得
如图,四边形ABCD中
(1)若AB∥CD,补充条件_____, 使四边形ABCD为平行四边形。
(2)若AD=BC,补充条件_____,使四边形ABCD为平行四边形。
AD∥BC
或者AB=CD
AD∥BC
或者AB=CD
练
1.填空:
C
B
D
A
2.请判断识别下列四边形是不是平行四边形?为什么?
⑶
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
A
D
C
B
110°
70°
110°
(2)
⑴
A
B
C
D
30°
30°
5 ㎝
5 ㎝
例:
如图,在平行四边形ABCD中,E、F分别是边BC和AD上的两点,且AF=CE。
求证:四边形AECF为平行四边形
B
A
C
D
F
E
证明:∵四边形ABCD是平行四边形
∴AD∥BC
即AF∥CE 又∵AF=CE
∴四边形AECF是平行四边形
(一组对边平行且相等的四边形是平行四边形)
你还有其他方法吗?
可求得△ABE≌△CDF(S.A.S)
∴AE=CF
又∵AF=CE
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
应用
如图,AB=CD,且∠DCA=∠BAC,四边形ABCD是平行四边形吗?你有几种判定方法?
小试牛刀
A
D
C
B
拓展
已知:如图,在平行四边形ABCD中,BE,DF分别是∠ABC,∠CDA的平分线。
求证:四边形BFDE是平行四边形。
A
D
C
B
E
F
3
2
1
2.两组对边分别相等的的四边形是平行四边形。
3.一组对边平行且相等的四边形是平行四边形。
1.定义:两组对边分别平行的四边形是平行四边形。
平行四边形的判定方法
1. 课本第85页练习第1,2, 3题;
习题18.2第1, 2题
2、预习下一节
课题:平行四边形的判定
你怎么确定这四边形就是平行四边形呢?
爸爸,你看我做的平行四边形。
你还记得吗?
两组对边分别平行的四边形是平行四边形
平行四边形的定义
忆
平行四边形的主要性质:
3、对角线: 平行四边形对角线互相平分.
1、边 :
a.平行四边形两组对边分别平行.
b.平行四边形两组对边分别相等.
两组对边分别平行的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
(定义)
平行四边形的判定方法1
猜
说
你能分别说出它们的逆命题吗?
这些逆命题成立吗?
2、角:平行四边形的对角相等,邻角互补.
两组对边分别平行的四边形是平行四边形
∵ AD∥BC,AB∥CD
∴ 四边形ABCD是平行四边形
数学语言:
C
B
D
A
平行四边形的判定方法1
两组对边分别相等的四边形是平行四边形
已知:如图在四边形ABCD中,AD=BC、AB=DC
求证:四边形ABCD是平行四边形
A
C
D
1
3
2
4
B
证
证明:连结AC
∵AD=BC,AB=DC,AC=AC
∴⊿ABC≌⊿CDA(S.S.S)
∴∠1= ∠2, ∠3=∠4 (全等三角形的性质)
∴AB∥CD,AD∥BC(内错角相等,两直线平行)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是 平行四边形)
命题:
平行四边形的判定方法2
C
B
D
A
数学语言:
∵ AB=CD,AD=BC,
∴ 四边形ABCD是平行四边形
探
你还能想到其他的判定方法吗?
一组对边平行且相等的四边形是平行四边形
一组对边平行,另一组对边相等的四边形是平行四边形
已知:如图、在四边形ABCD中,AB∥CD、AB=CD
求证:四边形ABCD是平行四边形
A
C
D
1
3
2
4
B
一组对边平行且相等的四边形是平行四边形
命题:
? 探索1
? 探索1结论
∵ AB∥CD,AB=CD,
∴ 四边形ABCD是平行四边形
C
B
D
A
一组对边平行且相等的 四边形是平行四边形.
数学语言:
“平行且相等”常用符号“ ”来表示
AB∥CD且AB=CD,记作“AB CD”
∥
=
读作:“AB平行且相等于CD”
∥
=
平行四边形的判定方法3
一组对边平行,另一组对边相等的四边形是平行四边形
命题:
? 探索2
C
B
D
A
C
B
D
A
是假命题
2.两组对边分别相等的四边形是平行四边形.
平行四边形的判定方法:
1.两组对边分别平行的四边形是平行四边形.(定义)
3.一组对边平行且相等的四边形是平行四边形.
得
如图,四边形ABCD中
(1)若AB∥CD,补充条件_____, 使四边形ABCD为平行四边形。
(2)若AD=BC,补充条件_____,使四边形ABCD为平行四边形。
AD∥BC
或者AB=CD
AD∥BC
或者AB=CD
练
1.填空:
C
B
D
A
2.请判断识别下列四边形是不是平行四边形?为什么?
⑶
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
A
D
C
B
110°
70°
110°
(2)
⑴
A
B
C
D
30°
30°
5 ㎝
5 ㎝
例:
如图,在平行四边形ABCD中,E、F分别是边BC和AD上的两点,且AF=CE。
求证:四边形AECF为平行四边形
B
A
C
D
F
E
证明:∵四边形ABCD是平行四边形
∴AD∥BC
即AF∥CE 又∵AF=CE
∴四边形AECF是平行四边形
(一组对边平行且相等的四边形是平行四边形)
你还有其他方法吗?
可求得△ABE≌△CDF(S.A.S)
∴AE=CF
又∵AF=CE
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
应用
如图,AB=CD,且∠DCA=∠BAC,四边形ABCD是平行四边形吗?你有几种判定方法?
小试牛刀
A
D
C
B
拓展
已知:如图,在平行四边形ABCD中,BE,DF分别是∠ABC,∠CDA的平分线。
求证:四边形BFDE是平行四边形。
A
D
C
B
E
F
3
2
1
2.两组对边分别相等的的四边形是平行四边形。
3.一组对边平行且相等的四边形是平行四边形。
1.定义:两组对边分别平行的四边形是平行四边形。
平行四边形的判定方法
1. 课本第85页练习第1,2, 3题;
习题18.2第1, 2题
2、预习下一节
