华东师大版八年级数学下册第20章20.3 .1数据的离散程度之方差教学课件 (共20张PPT)
文档属性
| 名称 | 华东师大版八年级数学下册第20章20.3 .1数据的离散程度之方差教学课件 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 249.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 09:55:42 | ||
图片预览




文档简介
华东师大版八年级数学下册
第二十章 数据的整理与初步处理
第三节 数据的离散程度
第一课时 方差
2月 21日
2月
22日
2月
23日
2月
24日
2月
25日
2月
26日
2月
27日
2月
28日
2001年
12
13
13
22
7
8
9
12
2002年
13
13
12
9
11
16
12
10
问题一:
下表显示的是2001年2月下旬和2002年2月同期的每日最高气温,如何对这两段时间的气温进行比较呢?
X2001=
(12+13+13+22+7+8+9+12)/8=12℃
X2002=
(13+13+12+9+11+16+12+10)/8 =12℃
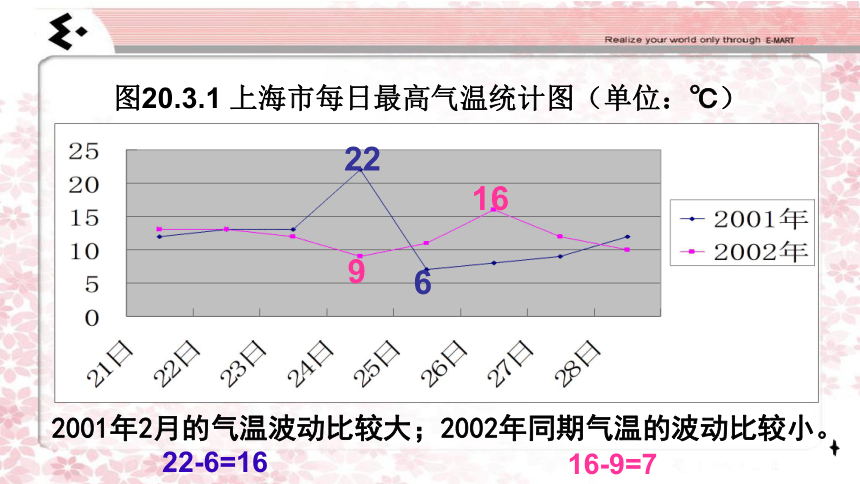
图20.3.1 上海市每日最高气温统计图(单位:℃)
9
22
6
16
2001年2月的气温波动比较大;2002年同期气温的波动比较小。
22-6=16
16-9=7
1、我们可以用一组数据中的最大值减去最小值所得的差来反映这组数据的变化范围.
用这种方法得到的差称为 。
2、极差=
3、极差越大,数据的波动性越 ;
大
小
极差越小,数据的波动性越 。
知识点一:
极 差
最大值-最小值
2、小明和小兵两人参加体育项目训练,近期的五
次测试成绩如表20.3.2所示.谁的成绩较为稳定?为什么?
测试次数
1
2
3
4
5
小明
10
14
13
12
13
小兵
11
11
15
14
11
表 20.3.2
X
12.4
12.4
极差
4
4
{7E9639D4-E3E2-4D34-9284-5A2195B3D0D7}
16
15
14
13
12
11
10
1
0
0 1 2 3 4 5 6
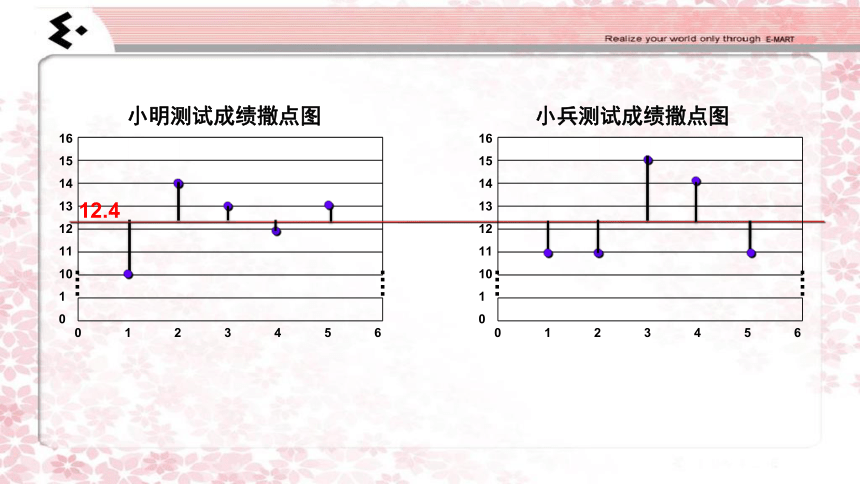
小明测试成绩撒点图
小兵测试成绩撒点图
12.4
{7E9639D4-E3E2-4D34-9284-5A2195B3D0D7}
16
15
14
13
12
11
10
1
0
0 1 2 3 4 5 6
{7E9639D4-E3E2-4D34-9284-5A2195B3D0D7}
16
15
14
13
12
11
10
1
0
0 1 2 3 4 5 6
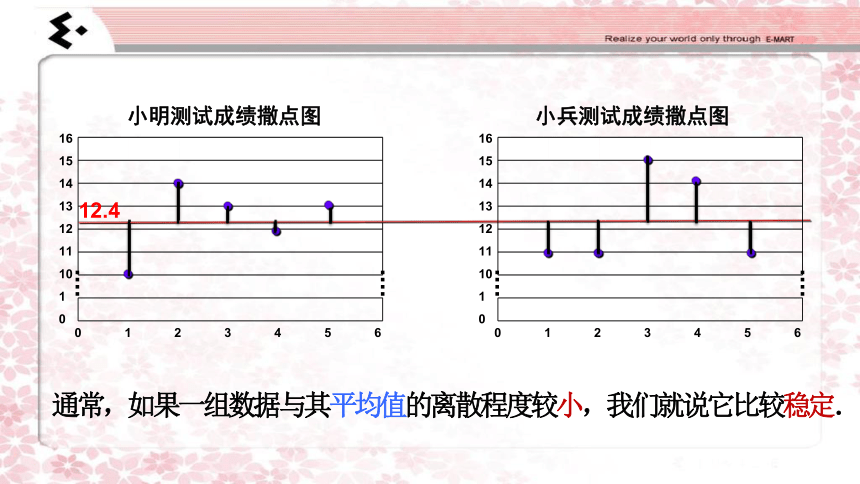
小明测试成绩撒点图
小兵测试成绩撒点图
12.4
{7E9639D4-E3E2-4D34-9284-5A2195B3D0D7}
16
15
14
13
12
11
10
1
0
0 1 2 3 4 5 6
通常,如果一组数据与其平均值的离散程度较小,我们就说它比较稳定.
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}
1
2
3
4
5
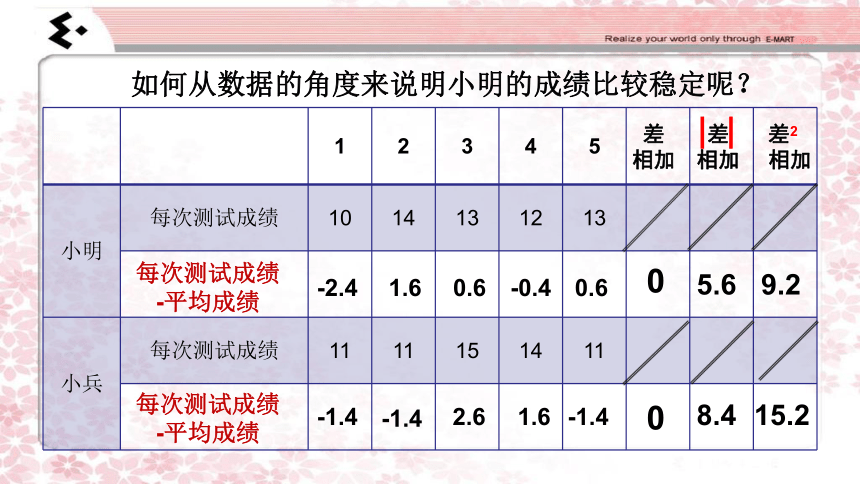
小明
每次测试成绩
10
14
13
12
13
小兵
每次测试成绩
11
11
15
14
11
-2.4
1.6
0.6
0.6
-0.4
-1.4
-1.4
2.6
1.6
-1.4
0
0
9.2
15.2
5.6
8.4
每次测试成绩
-平均成绩
每次测试成绩
-平均成绩
差
相加
差
相加
差2
相加
如何从数据的角度来说明小明的成绩比较稳定呢?
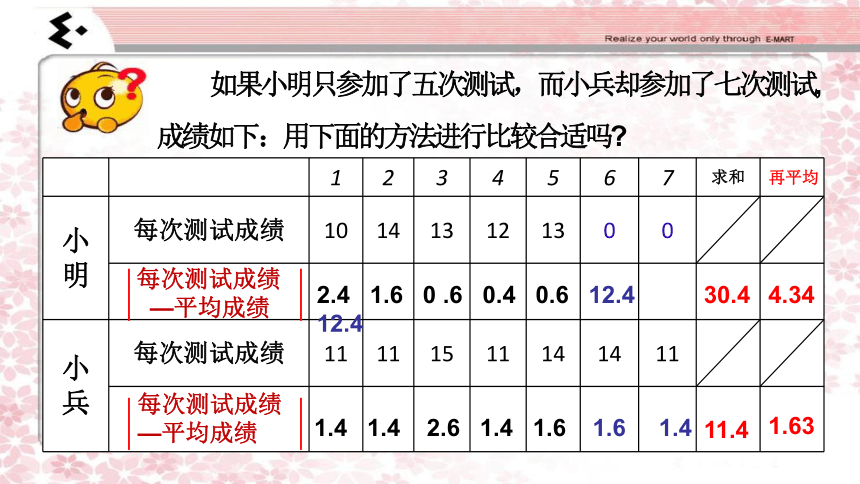
如果小明只参加了五次测试,而小兵却参加了七次测试,成绩如下:用下面的方法进行比较合适吗?
1
2
3
4
5
6
7
求和
小明
每次测试成绩
10
14
13
12
13
0
0
小兵
每次测试成绩
11
11
15
11
14
14
11
每次测试成绩
—平均成绩
每次测试成绩
—平均成绩
2.4 1.6 0 .6 0.4 0.6 12.4 12.4
1.4 1.4 2.6 1.4 1.6 1.6 1.4
11.4
30.4
再平均
4.34
1.63
1
2
3
4
5
6
7
求和
小明
每次测试成绩
10
14
13
12
13
小兵
每次测试成绩
11
11
15
11
14
14
11
每次测试成绩
—平均成绩
每次测试成绩
—平均成绩
2.4 1.6 0 .6 0.4 0.6
1.4 1.4 2.6 1.4 1.6 1.6 1.4
11.4
5.6
如何处理小明的缺考成绩会更公平些?
…..
如果小明参加了100次测试,而小兵却只参加了5次测试,成绩如下:把差的绝对值直接相加进行比较,公平吗?怎么处理才更合理呢?
1
2
3
4
5
…..
100
求和
小明
每次测试成绩
10
14
13
12
13
…...
13
小兵
每次测试成绩
11
11
15
11
14
每次测试成绩
—平均成绩
每次测试成绩
—平均成绩
2.4 1.6 0 .6 0.4 0.6 …… 0.6
1.4 1.4 2.6 1.4 1.6
8.4
105.6
再平均
1.06
1.68
1
2
3
4
5
6
7
求和
小明
每次测试成绩
10
14
13
12
13
0
0
小兵
每次测试成绩
11
11
15
11
14
14
11
(每次测试成绩—平均成绩)2
(每次测试成绩—平均成绩)2
5.76 2.56 0.36 0.16 0.36 153.76 153.76
1.96 1.96 6.76 1.96 2.56 2.56 1.96
313.12
17.72
如果小明只参加了五次测试,而小兵却参加了七次测试,成绩如下:用下面的方法进行比较合适吗?
1
2
3
4
5
……
100
求和
小明
每次测试成绩
10
14
13
12
13
…..
13
小兵
每次测试成绩
11
11
15
11
14
(每次测试成绩
—平均成绩)2
(每次测试成绩
—平均成绩)2
5.76 2.56 0.36 0.16 0.36 …… 0.36
1.96 1.96 6.76 1.96 2.56
173.2
15.2
1.73
3.04
再平均
如果小明参加了100次测试,而小兵却只参加了5次测试,成绩如下:把差的绝对值直接相加进行比较,公平吗?怎么处理才更合理呢?
※在一组数据中X1、X2 ,...... Xn中,各数据与它们的平均
值的差分别是:
※我们用差的平方的平均数:
-
-
-
-
-
-
(X1-X)2,(X2-X)2 ......(Xn-X)2,
1/n [(X1-X)2+(X2-X)2+......(Xn-X)2]
※来描述这组数据的离散程度,并把它叫做这组数据的方差, 用S2来表示。方差的公式表示为:
(X1-X),(X2-X), ......(Xn-X);
-
-
-
※差的平方是:
S2 =1/n [(X1-X)2+(X2-X)2+......(Xn-X)2]
-
-
-
测试次数
1
2
3
4
5
小明
10
14
13
12
13
小兵
11
11
15
14
11
请分别计算小明和小兵五次测试成绩的方差:
小试牛刀
新知运用
2、在学校,班级之间的常规评比是促进学生之间的团结进取的一种手段,现记录了八年级一班和二班10常规评比分如下:
一班:19.9 19.8 19.7 20.2 20.0 20.2 20.1 20.3 20.0 19.8
二班:19.7 20.2 19.8 19.9 19.7 20.3 20.1 20.0 19.8 20.2
分别计算两班的方差,并比较哪个班级的常规管理比较稳定。
巩固练习
某商店采购了一批直径为30mm的机器零件,从中抽样检查了10个零件的直径(单位:mm),结果如下:
30.0 29.8 30.1 30.2 29.9
30.0 30.2 29.8 30.0 30.0
如果样本的方差大于0.018就要退货,问:该商店是否需要退货?
本节课你有什么收获?
还有什么疑惑?
知识小结
知识小结
波动越 ,离散程度越 ,
方差或极差越小,
方差或极差越大,
一、方差的计算方法
通常用S2表示一组数据的方差,用 x 表示一组数据的平均数,x1、x2、…..表示各个数据。则有以下公式:
先平均,再求差,然后求差的平方,最后再平均。
二、方差的计算公式
S2 =1/n [(X1-X)2+(X2-X)2+......(Xn-X)2]
波动越 ,离散程度越 。
小
大
小
大
三、
2020年4月
第二十章 数据的整理与初步处理
第三节 数据的离散程度
第一课时 方差
2月 21日
2月
22日
2月
23日
2月
24日
2月
25日
2月
26日
2月
27日
2月
28日
2001年
12
13
13
22
7
8
9
12
2002年
13
13
12
9
11
16
12
10
问题一:
下表显示的是2001年2月下旬和2002年2月同期的每日最高气温,如何对这两段时间的气温进行比较呢?
X2001=
(12+13+13+22+7+8+9+12)/8=12℃
X2002=
(13+13+12+9+11+16+12+10)/8 =12℃
图20.3.1 上海市每日最高气温统计图(单位:℃)
9
22
6
16
2001年2月的气温波动比较大;2002年同期气温的波动比较小。
22-6=16
16-9=7
1、我们可以用一组数据中的最大值减去最小值所得的差来反映这组数据的变化范围.
用这种方法得到的差称为 。
2、极差=
3、极差越大,数据的波动性越 ;
大
小
极差越小,数据的波动性越 。
知识点一:
极 差
最大值-最小值
2、小明和小兵两人参加体育项目训练,近期的五
次测试成绩如表20.3.2所示.谁的成绩较为稳定?为什么?
测试次数
1
2
3
4
5
小明
10
14
13
12
13
小兵
11
11
15
14
11
表 20.3.2
X
12.4
12.4
极差
4
4
{7E9639D4-E3E2-4D34-9284-5A2195B3D0D7}
16
15
14
13
12
11
10
1
0
0 1 2 3 4 5 6
小明测试成绩撒点图
小兵测试成绩撒点图
12.4
{7E9639D4-E3E2-4D34-9284-5A2195B3D0D7}
16
15
14
13
12
11
10
1
0
0 1 2 3 4 5 6
{7E9639D4-E3E2-4D34-9284-5A2195B3D0D7}
16
15
14
13
12
11
10
1
0
0 1 2 3 4 5 6
小明测试成绩撒点图
小兵测试成绩撒点图
12.4
{7E9639D4-E3E2-4D34-9284-5A2195B3D0D7}
16
15
14
13
12
11
10
1
0
0 1 2 3 4 5 6
通常,如果一组数据与其平均值的离散程度较小,我们就说它比较稳定.
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}
1
2
3
4
5
小明
每次测试成绩
10
14
13
12
13
小兵
每次测试成绩
11
11
15
14
11
-2.4
1.6
0.6
0.6
-0.4
-1.4
-1.4
2.6
1.6
-1.4
0
0
9.2
15.2
5.6
8.4
每次测试成绩
-平均成绩
每次测试成绩
-平均成绩
差
相加
差
相加
差2
相加
如何从数据的角度来说明小明的成绩比较稳定呢?
如果小明只参加了五次测试,而小兵却参加了七次测试,成绩如下:用下面的方法进行比较合适吗?
1
2
3
4
5
6
7
求和
小明
每次测试成绩
10
14
13
12
13
0
0
小兵
每次测试成绩
11
11
15
11
14
14
11
每次测试成绩
—平均成绩
每次测试成绩
—平均成绩
2.4 1.6 0 .6 0.4 0.6 12.4 12.4
1.4 1.4 2.6 1.4 1.6 1.6 1.4
11.4
30.4
再平均
4.34
1.63
1
2
3
4
5
6
7
求和
小明
每次测试成绩
10
14
13
12
13
小兵
每次测试成绩
11
11
15
11
14
14
11
每次测试成绩
—平均成绩
每次测试成绩
—平均成绩
2.4 1.6 0 .6 0.4 0.6
1.4 1.4 2.6 1.4 1.6 1.6 1.4
11.4
5.6
如何处理小明的缺考成绩会更公平些?
…..
如果小明参加了100次测试,而小兵却只参加了5次测试,成绩如下:把差的绝对值直接相加进行比较,公平吗?怎么处理才更合理呢?
1
2
3
4
5
…..
100
求和
小明
每次测试成绩
10
14
13
12
13
…...
13
小兵
每次测试成绩
11
11
15
11
14
每次测试成绩
—平均成绩
每次测试成绩
—平均成绩
2.4 1.6 0 .6 0.4 0.6 …… 0.6
1.4 1.4 2.6 1.4 1.6
8.4
105.6
再平均
1.06
1.68
1
2
3
4
5
6
7
求和
小明
每次测试成绩
10
14
13
12
13
0
0
小兵
每次测试成绩
11
11
15
11
14
14
11
(每次测试成绩—平均成绩)2
(每次测试成绩—平均成绩)2
5.76 2.56 0.36 0.16 0.36 153.76 153.76
1.96 1.96 6.76 1.96 2.56 2.56 1.96
313.12
17.72
如果小明只参加了五次测试,而小兵却参加了七次测试,成绩如下:用下面的方法进行比较合适吗?
1
2
3
4
5
……
100
求和
小明
每次测试成绩
10
14
13
12
13
…..
13
小兵
每次测试成绩
11
11
15
11
14
(每次测试成绩
—平均成绩)2
(每次测试成绩
—平均成绩)2
5.76 2.56 0.36 0.16 0.36 …… 0.36
1.96 1.96 6.76 1.96 2.56
173.2
15.2
1.73
3.04
再平均
如果小明参加了100次测试,而小兵却只参加了5次测试,成绩如下:把差的绝对值直接相加进行比较,公平吗?怎么处理才更合理呢?
※在一组数据中X1、X2 ,...... Xn中,各数据与它们的平均
值的差分别是:
※我们用差的平方的平均数:
-
-
-
-
-
-
(X1-X)2,(X2-X)2 ......(Xn-X)2,
1/n [(X1-X)2+(X2-X)2+......(Xn-X)2]
※来描述这组数据的离散程度,并把它叫做这组数据的方差, 用S2来表示。方差的公式表示为:
(X1-X),(X2-X), ......(Xn-X);
-
-
-
※差的平方是:
S2 =1/n [(X1-X)2+(X2-X)2+......(Xn-X)2]
-
-
-
测试次数
1
2
3
4
5
小明
10
14
13
12
13
小兵
11
11
15
14
11
请分别计算小明和小兵五次测试成绩的方差:
小试牛刀
新知运用
2、在学校,班级之间的常规评比是促进学生之间的团结进取的一种手段,现记录了八年级一班和二班10常规评比分如下:
一班:19.9 19.8 19.7 20.2 20.0 20.2 20.1 20.3 20.0 19.8
二班:19.7 20.2 19.8 19.9 19.7 20.3 20.1 20.0 19.8 20.2
分别计算两班的方差,并比较哪个班级的常规管理比较稳定。
巩固练习
某商店采购了一批直径为30mm的机器零件,从中抽样检查了10个零件的直径(单位:mm),结果如下:
30.0 29.8 30.1 30.2 29.9
30.0 30.2 29.8 30.0 30.0
如果样本的方差大于0.018就要退货,问:该商店是否需要退货?
本节课你有什么收获?
还有什么疑惑?
知识小结
知识小结
波动越 ,离散程度越 ,
方差或极差越小,
方差或极差越大,
一、方差的计算方法
通常用S2表示一组数据的方差,用 x 表示一组数据的平均数,x1、x2、…..表示各个数据。则有以下公式:
先平均,再求差,然后求差的平方,最后再平均。
二、方差的计算公式
S2 =1/n [(X1-X)2+(X2-X)2+......(Xn-X)2]
波动越 ,离散程度越 。
小
大
小
大
三、
2020年4月
