华东师大版八年级下册18.1.1平行四边形的性质课件(共21张PPT)
文档属性
| 名称 | 华东师大版八年级下册18.1.1平行四边形的性质课件(共21张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 00:00:00 | ||
图片预览




文档简介
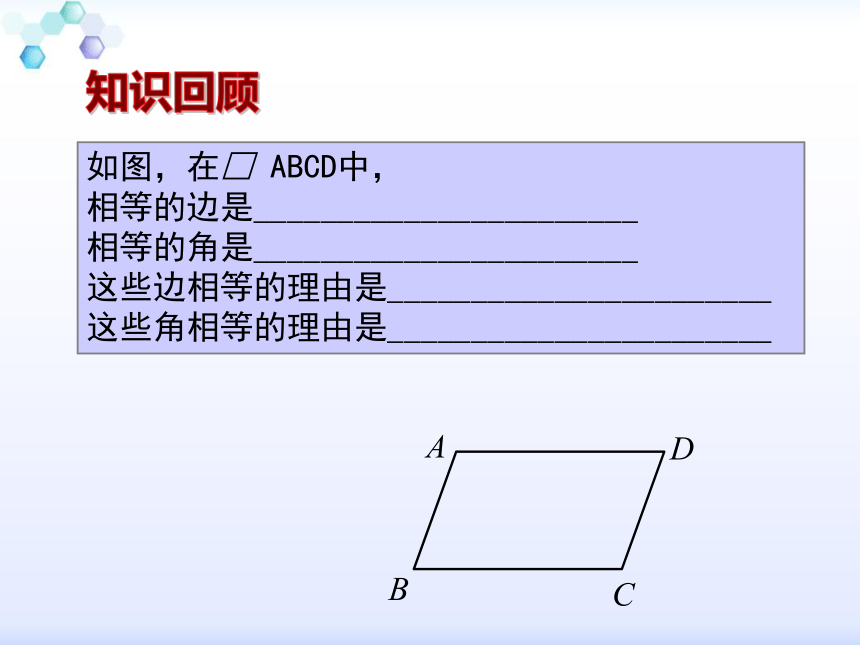
如图,要使四边形ABCD是平行四边形,
可以添加条件:_____________,
添加的理由是:_______________________。
B
C
D
A
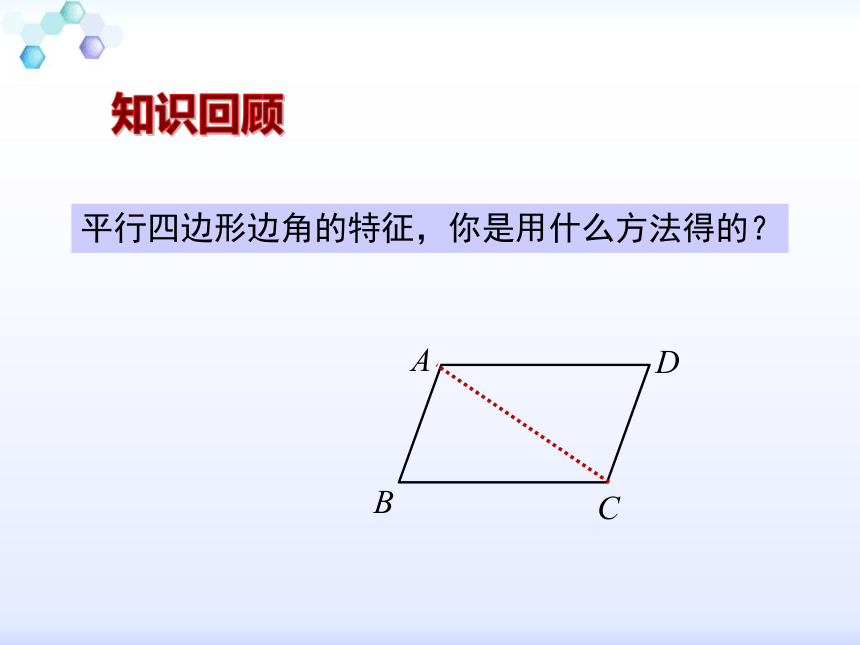
如图,在□ ABCD中,
相等的边是_______________________
相等的角是_______________________
这些边相等的理由是_______________________
这些角相等的理由是_______________________
B
C
D
A
平行四边形边角的特征,你是用什么方法得的?
B
C
D
A
学习目标
(一)知识与技能
掌握平行四边形对角线互相平分的性质。(重点)
(二)过程与方法
经历对平行四边形性质的猜想与证明的过程,渗透转化思想,体会图形性质探究的一般思路.(难点)?
(三)情感态度与价值观
学生在数学学习活动中获得成功的体验,激励他们锲而不舍的探究精神,形成积极参与、合作学习的学习习惯;通过平行四边形性质的应用,进一步认识数学与生活的密切联系。
平行四边形的对角线的性质
一
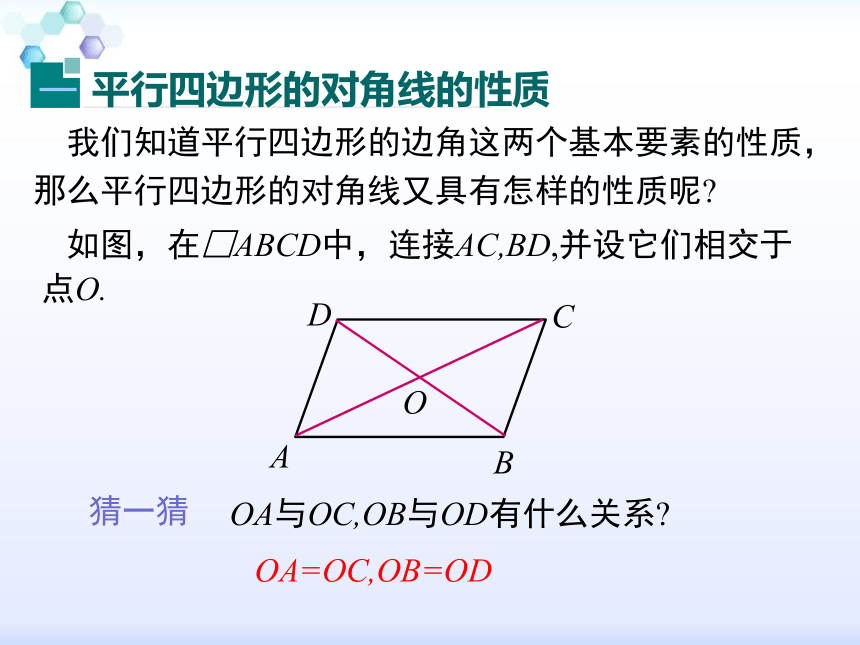
我们知道平行四边形的边角这两个基本要素的性质,那么平行四边形的对角线又具有怎样的性质呢?
A
B
C
D
O
如图,在□ABCD中,连接AC,BD,并设它们相交于点O.
OA与OC,OB与OD有什么关系?
猜一猜
OA=OC,OB=OD
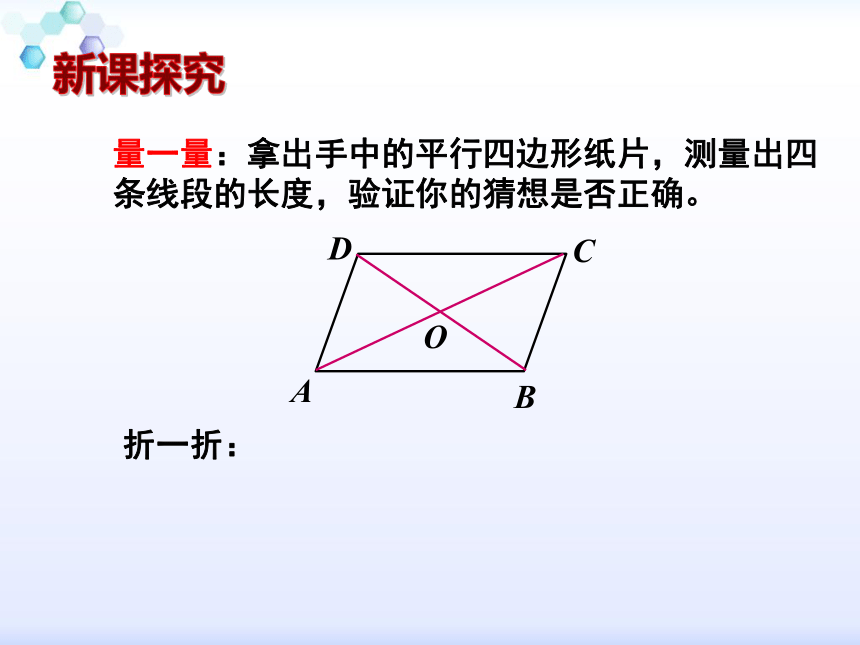
量一量:拿出手中的平行四边形纸片,测量出四条线段的长度,验证你的猜想是否正确。
折一折:
A
B
C
D
O
●
A
D
O
C
B
D
B
O
C
A
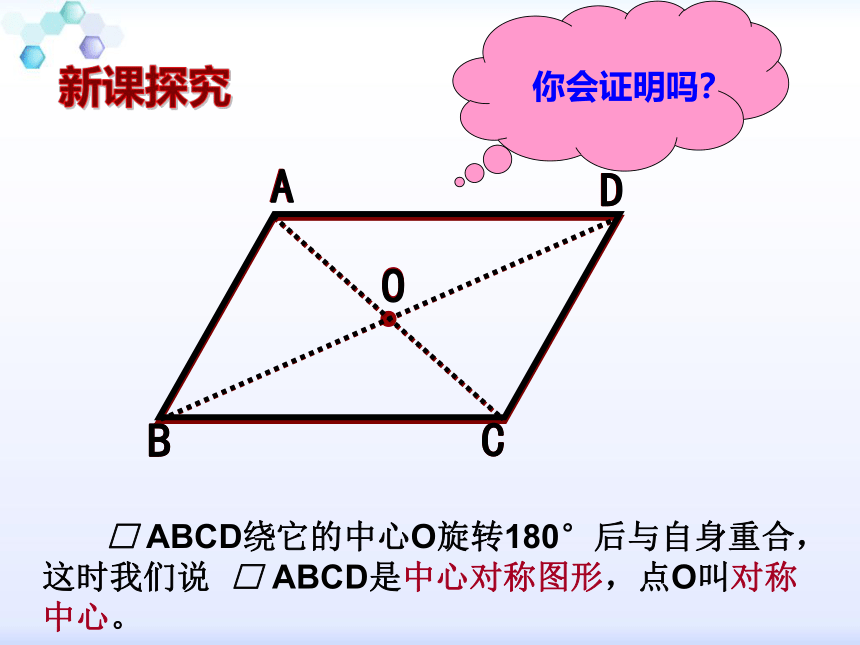
□ ABCD绕它的中心O旋转180°后与自身重合,这时我们说 □ ABCD是中心对称图形,点O叫对称中心。
你会证明吗?
已知:如图,□ ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
A
C
D
B
O
已知:如图,□ ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC,
∴ ∠1=∠2,∠3=∠4,
∴ △AOD≌△COB(ASA),
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
一位饱经苍桑的老人,经过一辈子的 辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为
自己的地少,同学们,你认为老人这样分合
理吗?为什么呢?
A
C
D
B
O
●
老大
老四
老三
老二
M
例6,如图, ABCD的对角线AC,BD交于点O.点O作直线EF,分别交AB,CD于点E,F.求证:OE=OF.
A
B
C
D
F
E
O
证明:∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE,
∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴AB∥CD, OD=OB,
∴OE=OF.
思考 改变直线EF的位置,OE=OF还成立吗?
议一议:在上述问题中,若直线EF与边AD、CB的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由.
●
O
F
E
(1)
(2)
●
O
D
C
B
A
F
E
●
●
A
B
C
D
F
E
O
●
O
C
B
A
D
E
F
●
O
C
B
A
D
E
F
(3)
(4)
议一议:
在上述问题中,若将直线EF绕点O旋转至下
图(3)、(4)的位置时,上述结论是否仍然成立?
●
●
●
●
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到的线段总相等.
请你为张师傅弹一条墨线,将锯下的这块平行四边形木板分成面积相等的两部分。你有多少种方法?
F
E
C
B
O
D
●
A
2
你能用一条直线把下面的图形分成面积相等的两部分吗?
课后作业
可以添加条件:_____________,
添加的理由是:_______________________。
B
C
D
A
如图,在□ ABCD中,
相等的边是_______________________
相等的角是_______________________
这些边相等的理由是_______________________
这些角相等的理由是_______________________
B
C
D
A
平行四边形边角的特征,你是用什么方法得的?
B
C
D
A
学习目标
(一)知识与技能
掌握平行四边形对角线互相平分的性质。(重点)
(二)过程与方法
经历对平行四边形性质的猜想与证明的过程,渗透转化思想,体会图形性质探究的一般思路.(难点)?
(三)情感态度与价值观
学生在数学学习活动中获得成功的体验,激励他们锲而不舍的探究精神,形成积极参与、合作学习的学习习惯;通过平行四边形性质的应用,进一步认识数学与生活的密切联系。
平行四边形的对角线的性质
一
我们知道平行四边形的边角这两个基本要素的性质,那么平行四边形的对角线又具有怎样的性质呢?
A
B
C
D
O
如图,在□ABCD中,连接AC,BD,并设它们相交于点O.
OA与OC,OB与OD有什么关系?
猜一猜
OA=OC,OB=OD
量一量:拿出手中的平行四边形纸片,测量出四条线段的长度,验证你的猜想是否正确。
折一折:
A
B
C
D
O
●
A
D
O
C
B
D
B
O
C
A
□ ABCD绕它的中心O旋转180°后与自身重合,这时我们说 □ ABCD是中心对称图形,点O叫对称中心。
你会证明吗?
已知:如图,□ ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
A
C
D
B
O
已知:如图,□ ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC,
∴ ∠1=∠2,∠3=∠4,
∴ △AOD≌△COB(ASA),
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
一位饱经苍桑的老人,经过一辈子的 辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为
自己的地少,同学们,你认为老人这样分合
理吗?为什么呢?
A
C
D
B
O
●
老大
老四
老三
老二
M
例6,如图, ABCD的对角线AC,BD交于点O.点O作直线EF,分别交AB,CD于点E,F.求证:OE=OF.
A
B
C
D
F
E
O
证明:∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE,
∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴AB∥CD, OD=OB,
∴OE=OF.
思考 改变直线EF的位置,OE=OF还成立吗?
议一议:在上述问题中,若直线EF与边AD、CB的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由.
●
O
F
E
(1)
(2)
●
O
D
C
B
A
F
E
●
●
A
B
C
D
F
E
O
●
O
C
B
A
D
E
F
●
O
C
B
A
D
E
F
(3)
(4)
议一议:
在上述问题中,若将直线EF绕点O旋转至下
图(3)、(4)的位置时,上述结论是否仍然成立?
●
●
●
●
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到的线段总相等.
请你为张师傅弹一条墨线,将锯下的这块平行四边形木板分成面积相等的两部分。你有多少种方法?
F
E
C
B
O
D
●
A
2
你能用一条直线把下面的图形分成面积相等的两部分吗?
课后作业
