华东师大版八年级下册18.1平行四边形性质 的应用 课件 (共25张PPT)
文档属性
| 名称 | 华东师大版八年级下册18.1平行四边形性质 的应用 课件 (共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 15:41:14 | ||
图片预览





文档简介
学习目标
重难点
1、掌握和运用平行四边形的性质;
2、能够综合运用平行四边形与全等三角形的解决问题;
3.利用中位线和辅助线来证明问题;
知识回顾
合作探究
拓展测试
谈谈收获
课后作业
学习目标
重难点
重点:综合运用平行四边形边、角、对角线的性质计算
难点:平行四边形的应用
知识回顾
合作探究
拓展测试
谈谈收获
课后作业
学习目标
重难点
知识回顾
两组对边分别平行的四边形叫平行四边形
2.平行四边形的性质 :
两组对边分别平行且相等。
边:
角:
两组对角分别相等,邻角互补
对角线:
对角线互相平分。
合作探究
拓展测试
谈谈收获
课后作业
1.定义:
学习目标
重难点
知识回顾
拓展测试
谈谈收获
课后作业
合作探究
合作探究
1.下列选项中不属于平行四边形性质的是( )
A.一组对角相等
B.对角线互相平分
C.一组对边平行且相等
D.对角线互相垂直
D
2、在 ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1
C.1:1:2:2 D.2:1:2:1
D
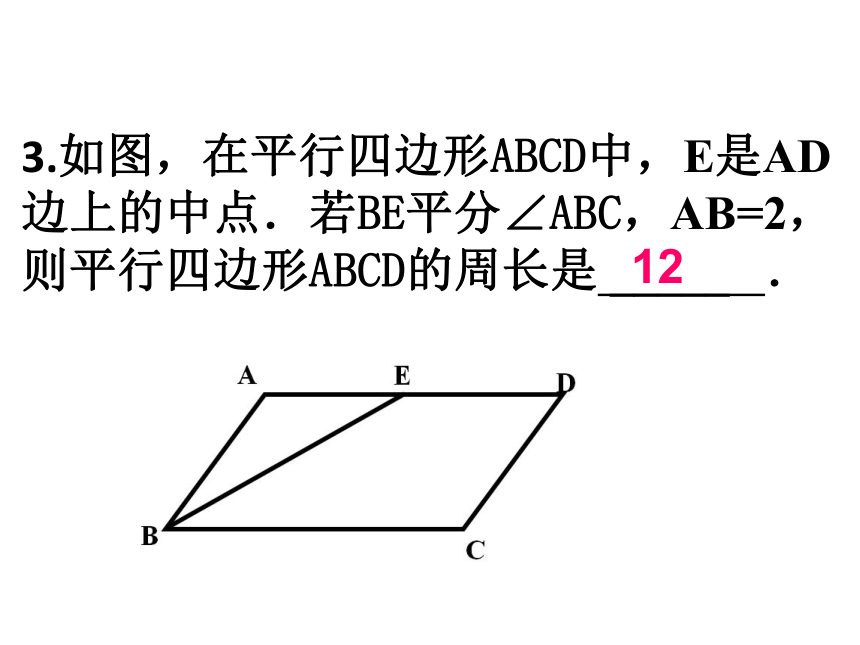
3.如图,在平行四边形ABCD中,E是AD边上的中点.若BE平分∠ABC,AB=2,
则平行四边形ABCD的周长是 _____ .
12
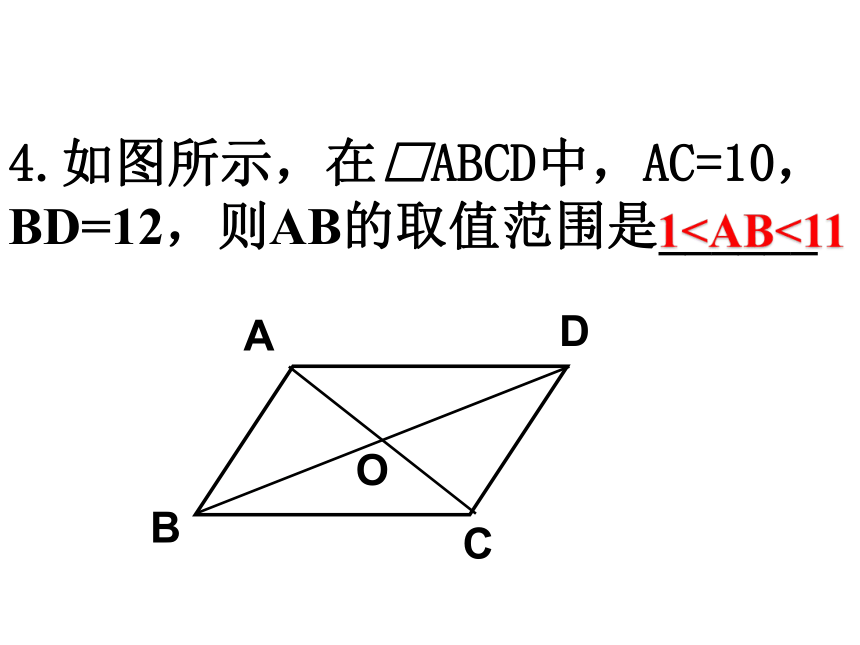
4.如图所示,在□ABCD中,AC=10,
BD=12,则AB的取值范围是______
B
C
D
A
O
5.如图,在□ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE且交AD于点F,则∠FCB=_____.
A
B
C
D
E
6.如图,在平面直角坐标系中, OBCD的顶点 O﹑B﹑D的坐标如图所示,则顶点C的 坐标为( )
x
Y
C
O (0,0)
B(5,0)
D(2,3)
A. (3,7) B. (5,3)
C. (7,3) D. (8,2)
C
7.在平面直角坐标系中,顶点 O﹑B﹑D的坐标如图所示,点C与A、B、D三点构成平行四边形,则C的 坐标为_______________________
x
Y
O (0,0)
B(5,0)
D(2,3)
(7,3)、(-3,3)、(3,-3)
学习目标
重难点
知识回顾
合作探究
谈谈收获
课后作业
拓展测试
拓展测试
8.如图,已知AB=AC.B是AD的中点,E是AB的中点,求证:CD=2CE.
学习目标
重难点
知识回顾
拓展测试
达标测试
课后作业
谈谈收获
通过本节课学习,你有何新的收获?
学习目标
重难点
知识回顾
拓展测试
达标测试
谈谈收获
课后作业
课堂同步练习册p40
7.如图,E、F是平行四边形ABCD对角线AC上两点,BE∥DF,
求证:AF=CE.
证明:∵四边形ABCD是平行四边形(已知)
∴ (平行四边形的对边平行且相等)
∴∠ACB=∠CAD(两直线平行,内错角相等)
∵BE∥DF(已知)
∴∠BEF=∠DFE(两直线平行,内错角相等)
在△BCE和△DAF中
∵∠BEF=∠DFE(已证)
∠ACB=∠CAD(已证)
BC=AD(已证)
∴△BCE ≌ △DAF(AAS)
∴CE=AF(全等三角形的对应边相等)
如图,已知点O是平行四边形ABCD的对角线AC的中点,四边形OCDE是平行四边形.求证:OE与AD互相平分.
课后习题
A
B
D
C
O
O
证明1:延长CE到F,使EF=CE.
∵E是AB的中点,
∴四边形ACBF为平行四边形.
∴
∴∠BAC=∠ABF.
∵AB=AC=BD,
∴∠ABC=∠ACB,BD=BF.
∵∠DBC=∠ACB+∠BAC=∠ABC+ABF=∠FBC,
∵BC=BC
∴△DBC ≌△FBC (SAS).
∴CD=CF=2CE.
F
证明2:如图,延长BC至P点,使CP=BC,连接AP
∵AB=AC,BD=AB
∴∠ABC=∠ACB,AC=BD
∴180°-∠ABC=180°-∠ACB
即:∠DBC=∠ACP
又∵BC=CP
∴△DBC ≌ △ACP(SAS)
∴AP=CD
∵AE=BE,BC=CP
∴CE为△ABP的中位线
∴CE=1/2AP ,∴CE=1/2CD
即:CD=2CE
p
证明3
取AC的中点F,连接BF。
∵E是AB的中点,F是AC的中点,
∴AE= AB,AF= AC,
∵AB=AC,∴AE=AF,
在△ABF和△ACE中,
∵AB=AC(已知),
∠BAF=∠CAE(公共角),
AF=AE(已证),
∴△ABF ≌ △ACE(SAS),∴BF=CE,
∵点B是AD的中点,点F是AC的中点,
∴BF是△ADC的中位线,
∴BF= CD,∴CE= CD。
F
证明4:
取CD的中点F,连接BF。
∵E是AB的中点,F是CD的中点,点B是AD的中点,
∴BF是△ADC的中位线,
∴BE= AB,BF= AC,,BF//AC
∵AB=AC,∴BE=BF,
又∵∠CBE=∠ACB,∠ABC==∠ACB
∴∠CBE=∠ABC
在△CBE和△CBF中,
∵ BE=BF(已知),
∠CBE=∠ABC(公共角), BC=BC(已证),
∴△ABF ≌ △ACE(SAS)
∴CD=CF= CD ,即CD=2CE
F
重难点
1、掌握和运用平行四边形的性质;
2、能够综合运用平行四边形与全等三角形的解决问题;
3.利用中位线和辅助线来证明问题;
知识回顾
合作探究
拓展测试
谈谈收获
课后作业
学习目标
重难点
重点:综合运用平行四边形边、角、对角线的性质计算
难点:平行四边形的应用
知识回顾
合作探究
拓展测试
谈谈收获
课后作业
学习目标
重难点
知识回顾
两组对边分别平行的四边形叫平行四边形
2.平行四边形的性质 :
两组对边分别平行且相等。
边:
角:
两组对角分别相等,邻角互补
对角线:
对角线互相平分。
合作探究
拓展测试
谈谈收获
课后作业
1.定义:
学习目标
重难点
知识回顾
拓展测试
谈谈收获
课后作业
合作探究
合作探究
1.下列选项中不属于平行四边形性质的是( )
A.一组对角相等
B.对角线互相平分
C.一组对边平行且相等
D.对角线互相垂直
D
2、在 ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1
C.1:1:2:2 D.2:1:2:1
D
3.如图,在平行四边形ABCD中,E是AD边上的中点.若BE平分∠ABC,AB=2,
则平行四边形ABCD的周长是 _____ .
12
4.如图所示,在□ABCD中,AC=10,
BD=12,则AB的取值范围是______
B
C
D
A
O
5.如图,在□ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE且交AD于点F,则∠FCB=_____.
A
B
C
D
E
6.如图,在平面直角坐标系中, OBCD的顶点 O﹑B﹑D的坐标如图所示,则顶点C的 坐标为( )
x
Y
C
O (0,0)
B(5,0)
D(2,3)
A. (3,7) B. (5,3)
C. (7,3) D. (8,2)
C
7.在平面直角坐标系中,顶点 O﹑B﹑D的坐标如图所示,点C与A、B、D三点构成平行四边形,则C的 坐标为_______________________
x
Y
O (0,0)
B(5,0)
D(2,3)
(7,3)、(-3,3)、(3,-3)
学习目标
重难点
知识回顾
合作探究
谈谈收获
课后作业
拓展测试
拓展测试
8.如图,已知AB=AC.B是AD的中点,E是AB的中点,求证:CD=2CE.
学习目标
重难点
知识回顾
拓展测试
达标测试
课后作业
谈谈收获
通过本节课学习,你有何新的收获?
学习目标
重难点
知识回顾
拓展测试
达标测试
谈谈收获
课后作业
课堂同步练习册p40
7.如图,E、F是平行四边形ABCD对角线AC上两点,BE∥DF,
求证:AF=CE.
证明:∵四边形ABCD是平行四边形(已知)
∴ (平行四边形的对边平行且相等)
∴∠ACB=∠CAD(两直线平行,内错角相等)
∵BE∥DF(已知)
∴∠BEF=∠DFE(两直线平行,内错角相等)
在△BCE和△DAF中
∵∠BEF=∠DFE(已证)
∠ACB=∠CAD(已证)
BC=AD(已证)
∴△BCE ≌ △DAF(AAS)
∴CE=AF(全等三角形的对应边相等)
如图,已知点O是平行四边形ABCD的对角线AC的中点,四边形OCDE是平行四边形.求证:OE与AD互相平分.
课后习题
A
B
D
C
O
O
证明1:延长CE到F,使EF=CE.
∵E是AB的中点,
∴四边形ACBF为平行四边形.
∴
∴∠BAC=∠ABF.
∵AB=AC=BD,
∴∠ABC=∠ACB,BD=BF.
∵∠DBC=∠ACB+∠BAC=∠ABC+ABF=∠FBC,
∵BC=BC
∴△DBC ≌△FBC (SAS).
∴CD=CF=2CE.
F
证明2:如图,延长BC至P点,使CP=BC,连接AP
∵AB=AC,BD=AB
∴∠ABC=∠ACB,AC=BD
∴180°-∠ABC=180°-∠ACB
即:∠DBC=∠ACP
又∵BC=CP
∴△DBC ≌ △ACP(SAS)
∴AP=CD
∵AE=BE,BC=CP
∴CE为△ABP的中位线
∴CE=1/2AP ,∴CE=1/2CD
即:CD=2CE
p
证明3
取AC的中点F,连接BF。
∵E是AB的中点,F是AC的中点,
∴AE= AB,AF= AC,
∵AB=AC,∴AE=AF,
在△ABF和△ACE中,
∵AB=AC(已知),
∠BAF=∠CAE(公共角),
AF=AE(已证),
∴△ABF ≌ △ACE(SAS),∴BF=CE,
∵点B是AD的中点,点F是AC的中点,
∴BF是△ADC的中位线,
∴BF= CD,∴CE= CD。
F
证明4:
取CD的中点F,连接BF。
∵E是AB的中点,F是CD的中点,点B是AD的中点,
∴BF是△ADC的中位线,
∴BE= AB,BF= AC,,BF//AC
∵AB=AC,∴BE=BF,
又∵∠CBE=∠ACB,∠ABC==∠ACB
∴∠CBE=∠ABC
在△CBE和△CBF中,
∵ BE=BF(已知),
∠CBE=∠ABC(公共角), BC=BC(已证),
∴△ABF ≌ △ACE(SAS)
∴CD=CF= CD ,即CD=2CE
F
