华东师大版八年级下册19.1.1 矩形的性质课件(34张PPT)
文档属性
| 名称 | 华东师大版八年级下册19.1.1 矩形的性质课件(34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 15:41:17 | ||
图片预览






文档简介
华师版《义务教育教科书》
19.1.1 矩形的性质
河南省淮阳县西城中学
数学组
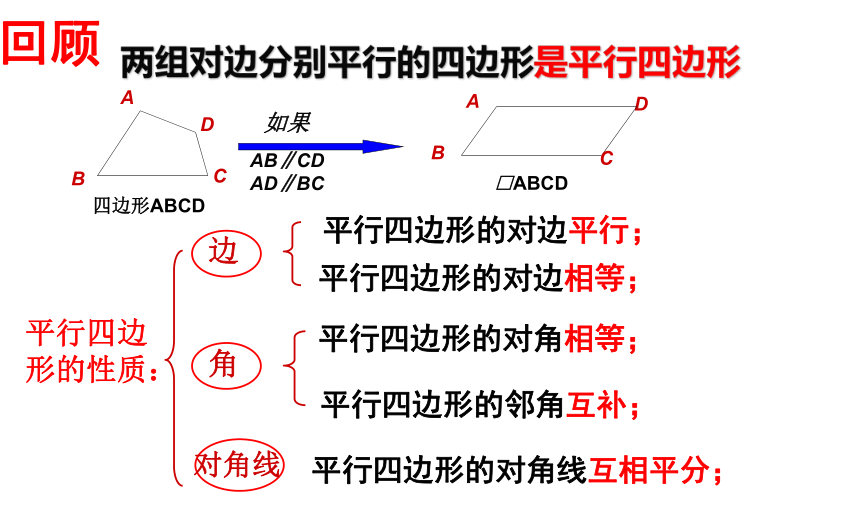
两组对边分别平行的四边形是平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
□ABCD
A
C
平行四边形的性质:
边
平行四边形的对边平行;
平行四边形的对边相等;
角
平行四边形的对角相等;
平行四边形的邻角互补;
对角线
平行四边形的对角线互相平分;
回顾
19.1.1矩形的性质
学习目标
1.探索并掌握矩形的定义和性质。
2.会运用矩形的定义和性质进行有关的论证和计算。
重点:掌握矩形的定义和性质
难点:灵活运用矩形的定义和性质进行有关的论证和计算。
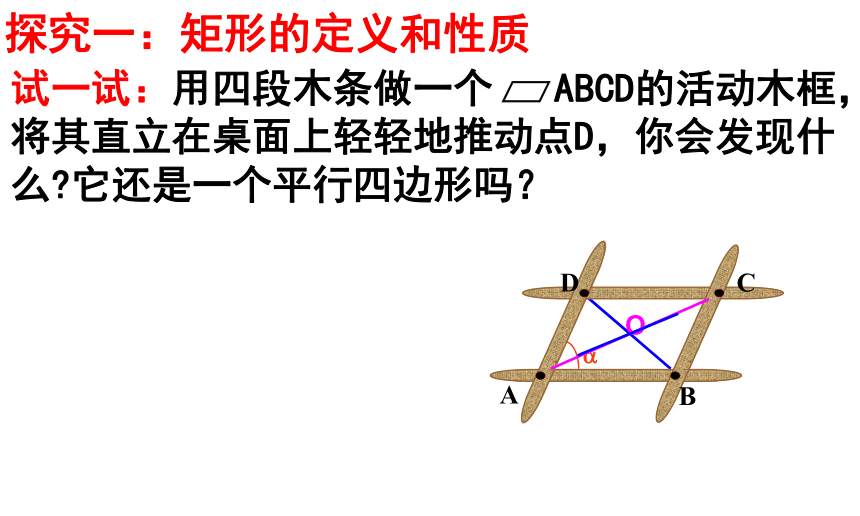
探究一:矩形的定义和性质
自学指导(时间5分钟)
内容:阅读课本P98—99, 完成试一试并思考
问题:
(1) 什么样的图形叫做矩形?
(2) 矩形是什么对称图形?对称轴有几条?
(3) 矩形的性质有哪些?
试一试:用四段木条做一个 ABCD的活动木框,将其直立在桌面上轻轻地推动点D,你会发现什么?它还是一个平行四边形吗?
?
O
D
A
C
B
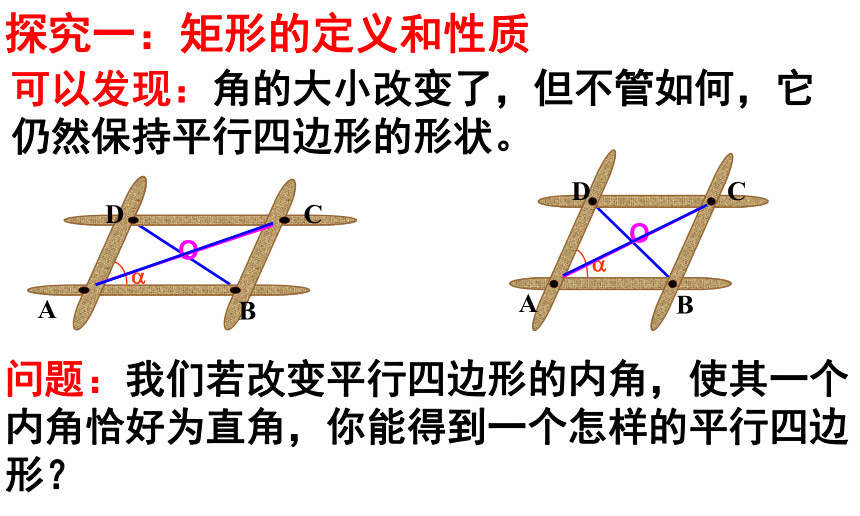
探究一:矩形的定义和性质
可以发现:角的大小改变了,但不管如何,它仍然保持平行四边形的形状。
探究一:矩形的定义和性质
?
O
D
A
C
B
?
O
D
A
C
B
问题:我们若改变平行四边形的内角,使其一个内角恰好为直角,你能得到一个怎样的平行四边形?
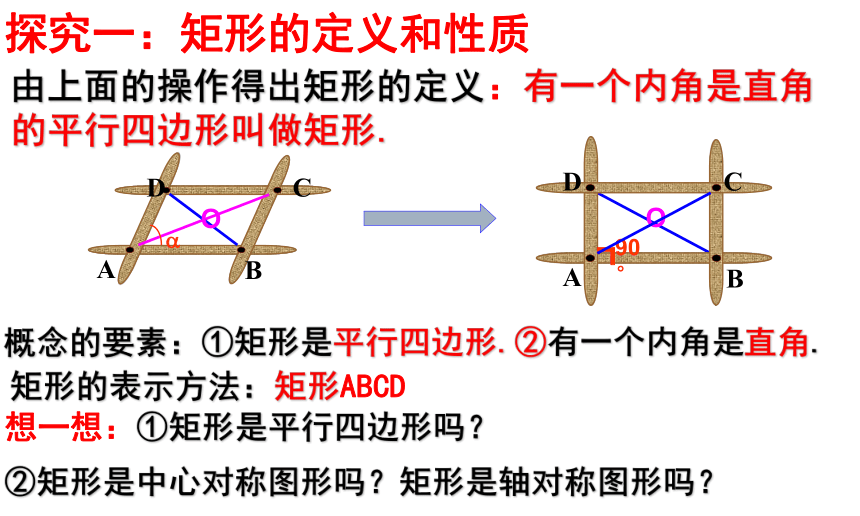
由上面的操作得出矩形的定义:有一个内角是直角的平行四边形叫做矩形.
D
A
C
B
?
O
D
A
C
B
O
┓
90°
探究一:矩形的定义和性质
概念的要素:①矩形是平行四边形.②有一个内角是直角.
矩形的表示方法:矩形ABCD
想一想:①矩形是平行四边形吗?
②矩形是中心对称图形吗?矩形是轴对称图形吗?
思考:
问题1:矩形是特殊的平行四边形,它是否具有平行四边形的一切性质?
问题2:矩形既然是特殊的平行四边形,它有没有特殊的性质?
探究一:矩形的定义和性质
A
B
C
D
O
角
边
对角线
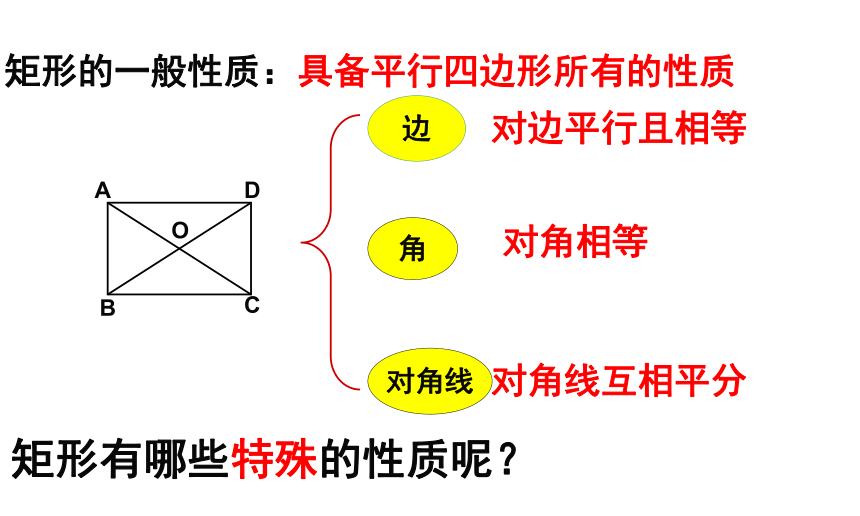
对边平行且相等
对角相等
对角线互相平分
矩形的一般性质:具备平行四边形所有的性质
矩形有哪些特殊的性质呢?
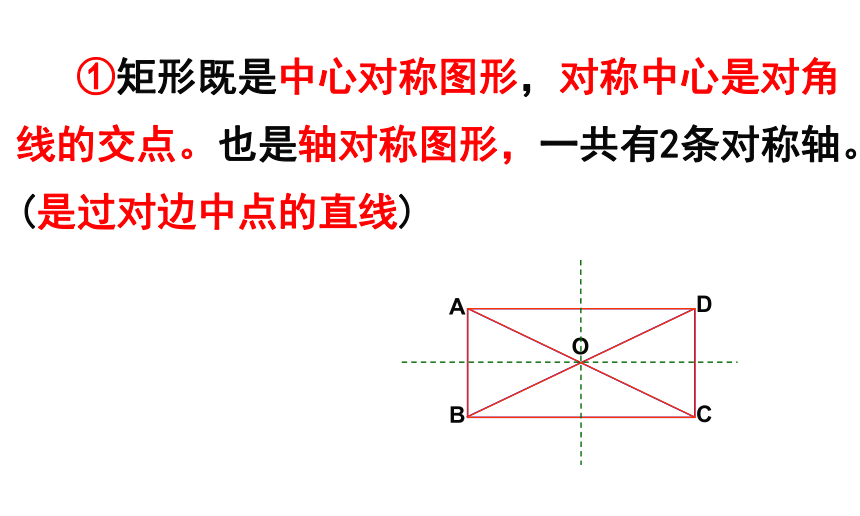
①矩形既是中心对称图形,对称中心是对角线的交点。也是轴对称图形,一共有2条对称轴。(是过对边中点的直线)
A
B
C
D
O
② 矩形的四个内角都是直角.
③矩形的对角线相等且互相平分.
矩形ABCD
┒
┒
┒
┒
A
B
C
D
O
你能证明矩形的特有性质吗?
矩形的四个角都是直角
已知:矩形ABCD
求证:∠A=∠B=∠C=∠D
A
B
C
D
矩形的四个角都是直角
已知:矩形ABCD
求证:∠A=∠B=∠C=∠D
A
B
C
D
证明:∵四边形ABCD是矩形
∴设∠A=90°
∴∠C=∠A=90°
∵AD∥BC
∴∠A+∠B=180°∠C+∠D=180°
∴∠B=180°-∠A=90°
∠D=180°-∠C=90°
∠A=∠B=∠C=∠D=90°
已知:如图,四边形ABCD是矩形
求证:AC = BD
A
B
C
D
求证:矩形的对角线相等。
矩形的对角线相等
已知:如图,四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:∵四边形ABCD是矩形
∴∠ABC = ∠DCB = 90°
在△ABC与△DCB中
AB = DC
∠ABC = ∠DCB = 90°
BC = CB
∴△ABC≌△DCB
∴AC = BD 即矩形的对角线相等
邻边:
四个角都是直角
互相平分 AO=CO; BO=DO
(1)边:
(2)角:
(3)对角线:
对边:
(共性)
(共性)
(个性)
(个性)
(个性)
(共性)
矩形性质与平行四边形性质比较:
平行 AD∥BC; AB∥ CD
相等 AB=CD; AD=BC
相 等 AC=BD
互相垂直 AB⊥BC; AB ⊥ AD
OA=OB=OC=OD 等于相等的对角线的一半
对角相等、邻角互补
(共性)
4.下列性质中,矩形不一定具有的是( )
A、对角线相等 B、 四个角都相等
C、对角线垂直 D、是轴对称图形
1.矩形的定义中有两个条件:一是____________,二是______________。
2.有一个角是直角的四边形是矩形。( )
3.矩形的对角线互相平分。( )
巩固训练:
4.下列性质中,矩形不一定具有的是( )
A、对角线相等 B、 四个角都相等
C、对角线垂直 D、是轴对称图形
1.矩形的定义中有两个条件:一是____________,二是______________。
2.有一个角是直角的四边形是矩形。( )
3.矩形的对角线互相平分。( )
平行四边形
有一个角是直角
√
×
C
巩固训练:
5.矩形具有而平行四边形不具有的性质是( )
A 两组对边分别平行 B 对角相等
C 对角线互相平分 D 对角线相等
6.矩形ABCD中,对角线AC、BD把矩形分成( )个等腰三角形,( )个直角三角形。
(A)2 (B)4 (C)6 (D)8
O
A
B
D
C
5.矩形具有而平行四边形不具有的性质是( )
A 两组对边分别平行 B 对角相等
C 对角线互相平分 D 对角线相等
6.矩形ABCD中,对角线AC、BD把矩形分成( )个等腰三角形,( )个直角三角形。
(A)2 (B)4 (C)6 (D)8
D
B
B
O
A
B
D
C
7.如图,在矩形ABCD中,对角线AC与BD相交于点O,试找出图中相等的线段和角。
巩固训练:
A
B
C
D
O
7.如图,在矩形ABCD中,对角线AC与BD相交于点O,试找出图中相等的线段和角。
巩固训练:
A
B
C
D
O
解:相等的线段:AB=CD ,BC=AD,BD=AC,
OA=OC=OB=OD
相等的角:∠ABC=∠BCD=∠CDA=∠DAB ,
∠OAD=∠ODA=∠OBC=∠OCB,
∠OBA=∠OBA=∠ODC=∠OCD
∠BOC=∠AOD,∠AOB=∠COD
探究点二:矩形性质的应用
自学指导:
内容:课本99页例1 时间:4分钟
要求:
1、阅读例2的解题过程
2、体会性质定理在解题过程中的应用
例1 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
O
A
B
D
C
例1 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
解: ∵ △AOB、 △BOC、 △COD和△AOD四个三角形的周长和为86cm,即 AB+BC+CD+DA+2(AC+BD) =86
又∵ AC=BD=13cm(矩形的对角线相等)
∴ AB+BC+CD+DA = 86-2(AC+BD)
= 86-2×2×13= 34(cm)
即矩形ABCD的周长等于34cm。
O
A
B
D
C
巩固训练
1.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOD=120°,求证AC=2AB
A
B
C
D
O
1.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOD=120°,求证AC=2AB
A
B
C
D
O
证明:在矩形ABCD中,
AC=BD,OC=OA= AC
OB=OD= BD,
∴OA=OB
∵∠AOD=120°
∴∠AOB=180°-∠AOD=60°
∴△OAB是等边三角形 即AB=OA= AC
∴AC=2AB
巩固训练
2.如图,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB= 60°,AC=16,则图中长度为8的线段有( )
A.2条 B.4条 C.5条 D.6条
A
B
O
C
D
60°
2.如图,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB= 60°,AC=16,则图中长度为8的线段有( D )
A.2条 B.4条 C.5条 D.6条
A
B
O
C
D
60°
3.如图,矩形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果∠ BAF=60° ,求∠DAE的度数。
3.如图,矩形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果∠ BAF=60° ,求∠DAE的度数。
解:在矩形ABCD中
∵∠BAF=60°,
∴∠DAF=30°,
又∵AF是AD折叠得到的,
∴∠DAE=∠EAF=15°.
故∠DAE=15.
课堂小结:
19.1.1 矩形的性质
河南省淮阳县西城中学
数学组
两组对边分别平行的四边形是平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
□ABCD
A
C
平行四边形的性质:
边
平行四边形的对边平行;
平行四边形的对边相等;
角
平行四边形的对角相等;
平行四边形的邻角互补;
对角线
平行四边形的对角线互相平分;
回顾
19.1.1矩形的性质
学习目标
1.探索并掌握矩形的定义和性质。
2.会运用矩形的定义和性质进行有关的论证和计算。
重点:掌握矩形的定义和性质
难点:灵活运用矩形的定义和性质进行有关的论证和计算。
探究一:矩形的定义和性质
自学指导(时间5分钟)
内容:阅读课本P98—99, 完成试一试并思考
问题:
(1) 什么样的图形叫做矩形?
(2) 矩形是什么对称图形?对称轴有几条?
(3) 矩形的性质有哪些?
试一试:用四段木条做一个 ABCD的活动木框,将其直立在桌面上轻轻地推动点D,你会发现什么?它还是一个平行四边形吗?
?
O
D
A
C
B
探究一:矩形的定义和性质
可以发现:角的大小改变了,但不管如何,它仍然保持平行四边形的形状。
探究一:矩形的定义和性质
?
O
D
A
C
B
?
O
D
A
C
B
问题:我们若改变平行四边形的内角,使其一个内角恰好为直角,你能得到一个怎样的平行四边形?
由上面的操作得出矩形的定义:有一个内角是直角的平行四边形叫做矩形.
D
A
C
B
?
O
D
A
C
B
O
┓
90°
探究一:矩形的定义和性质
概念的要素:①矩形是平行四边形.②有一个内角是直角.
矩形的表示方法:矩形ABCD
想一想:①矩形是平行四边形吗?
②矩形是中心对称图形吗?矩形是轴对称图形吗?
思考:
问题1:矩形是特殊的平行四边形,它是否具有平行四边形的一切性质?
问题2:矩形既然是特殊的平行四边形,它有没有特殊的性质?
探究一:矩形的定义和性质
A
B
C
D
O
角
边
对角线
对边平行且相等
对角相等
对角线互相平分
矩形的一般性质:具备平行四边形所有的性质
矩形有哪些特殊的性质呢?
①矩形既是中心对称图形,对称中心是对角线的交点。也是轴对称图形,一共有2条对称轴。(是过对边中点的直线)
A
B
C
D
O
② 矩形的四个内角都是直角.
③矩形的对角线相等且互相平分.
矩形ABCD
┒
┒
┒
┒
A
B
C
D
O
你能证明矩形的特有性质吗?
矩形的四个角都是直角
已知:矩形ABCD
求证:∠A=∠B=∠C=∠D
A
B
C
D
矩形的四个角都是直角
已知:矩形ABCD
求证:∠A=∠B=∠C=∠D
A
B
C
D
证明:∵四边形ABCD是矩形
∴设∠A=90°
∴∠C=∠A=90°
∵AD∥BC
∴∠A+∠B=180°∠C+∠D=180°
∴∠B=180°-∠A=90°
∠D=180°-∠C=90°
∠A=∠B=∠C=∠D=90°
已知:如图,四边形ABCD是矩形
求证:AC = BD
A
B
C
D
求证:矩形的对角线相等。
矩形的对角线相等
已知:如图,四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:∵四边形ABCD是矩形
∴∠ABC = ∠DCB = 90°
在△ABC与△DCB中
AB = DC
∠ABC = ∠DCB = 90°
BC = CB
∴△ABC≌△DCB
∴AC = BD 即矩形的对角线相等
邻边:
四个角都是直角
互相平分 AO=CO; BO=DO
(1)边:
(2)角:
(3)对角线:
对边:
(共性)
(共性)
(个性)
(个性)
(个性)
(共性)
矩形性质与平行四边形性质比较:
平行 AD∥BC; AB∥ CD
相等 AB=CD; AD=BC
相 等 AC=BD
互相垂直 AB⊥BC; AB ⊥ AD
OA=OB=OC=OD 等于相等的对角线的一半
对角相等、邻角互补
(共性)
4.下列性质中,矩形不一定具有的是( )
A、对角线相等 B、 四个角都相等
C、对角线垂直 D、是轴对称图形
1.矩形的定义中有两个条件:一是____________,二是______________。
2.有一个角是直角的四边形是矩形。( )
3.矩形的对角线互相平分。( )
巩固训练:
4.下列性质中,矩形不一定具有的是( )
A、对角线相等 B、 四个角都相等
C、对角线垂直 D、是轴对称图形
1.矩形的定义中有两个条件:一是____________,二是______________。
2.有一个角是直角的四边形是矩形。( )
3.矩形的对角线互相平分。( )
平行四边形
有一个角是直角
√
×
C
巩固训练:
5.矩形具有而平行四边形不具有的性质是( )
A 两组对边分别平行 B 对角相等
C 对角线互相平分 D 对角线相等
6.矩形ABCD中,对角线AC、BD把矩形分成( )个等腰三角形,( )个直角三角形。
(A)2 (B)4 (C)6 (D)8
O
A
B
D
C
5.矩形具有而平行四边形不具有的性质是( )
A 两组对边分别平行 B 对角相等
C 对角线互相平分 D 对角线相等
6.矩形ABCD中,对角线AC、BD把矩形分成( )个等腰三角形,( )个直角三角形。
(A)2 (B)4 (C)6 (D)8
D
B
B
O
A
B
D
C
7.如图,在矩形ABCD中,对角线AC与BD相交于点O,试找出图中相等的线段和角。
巩固训练:
A
B
C
D
O
7.如图,在矩形ABCD中,对角线AC与BD相交于点O,试找出图中相等的线段和角。
巩固训练:
A
B
C
D
O
解:相等的线段:AB=CD ,BC=AD,BD=AC,
OA=OC=OB=OD
相等的角:∠ABC=∠BCD=∠CDA=∠DAB ,
∠OAD=∠ODA=∠OBC=∠OCB,
∠OBA=∠OBA=∠ODC=∠OCD
∠BOC=∠AOD,∠AOB=∠COD
探究点二:矩形性质的应用
自学指导:
内容:课本99页例1 时间:4分钟
要求:
1、阅读例2的解题过程
2、体会性质定理在解题过程中的应用
例1 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
O
A
B
D
C
例1 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
解: ∵ △AOB、 △BOC、 △COD和△AOD四个三角形的周长和为86cm,即 AB+BC+CD+DA+2(AC+BD) =86
又∵ AC=BD=13cm(矩形的对角线相等)
∴ AB+BC+CD+DA = 86-2(AC+BD)
= 86-2×2×13= 34(cm)
即矩形ABCD的周长等于34cm。
O
A
B
D
C
巩固训练
1.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOD=120°,求证AC=2AB
A
B
C
D
O
1.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOD=120°,求证AC=2AB
A
B
C
D
O
证明:在矩形ABCD中,
AC=BD,OC=OA= AC
OB=OD= BD,
∴OA=OB
∵∠AOD=120°
∴∠AOB=180°-∠AOD=60°
∴△OAB是等边三角形 即AB=OA= AC
∴AC=2AB
巩固训练
2.如图,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB= 60°,AC=16,则图中长度为8的线段有( )
A.2条 B.4条 C.5条 D.6条
A
B
O
C
D
60°
2.如图,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB= 60°,AC=16,则图中长度为8的线段有( D )
A.2条 B.4条 C.5条 D.6条
A
B
O
C
D
60°
3.如图,矩形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果∠ BAF=60° ,求∠DAE的度数。
3.如图,矩形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果∠ BAF=60° ,求∠DAE的度数。
解:在矩形ABCD中
∵∠BAF=60°,
∴∠DAF=30°,
又∵AF是AD折叠得到的,
∴∠DAE=∠EAF=15°.
故∠DAE=15.
课堂小结:
