华东师大版八年级下册19.1.1 矩形的性质课件(共23张PPT)
文档属性
| 名称 | 华东师大版八年级下册19.1.1 矩形的性质课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 15:41:21 | ||
图片预览


文档简介
矩形的性质
数学华师大版 八年级下
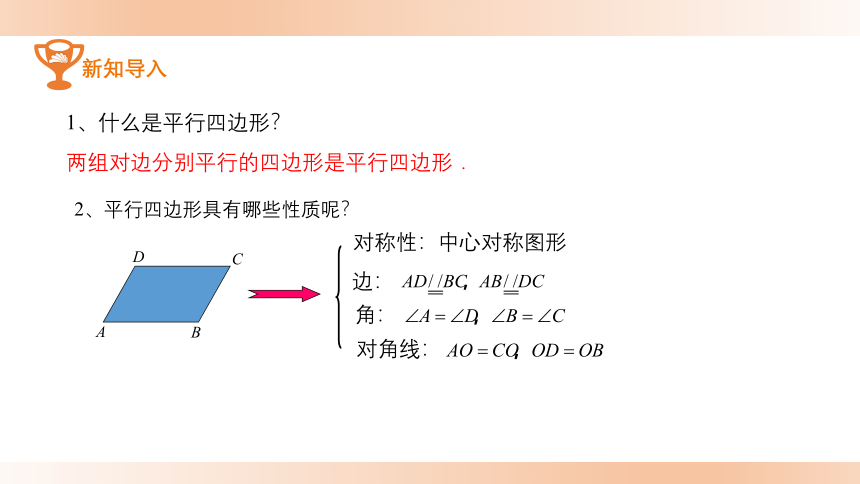
新知导入
1、什么是平行四边形?
两组对边分别平行的四边形是平行四边形.
2、平行四边形具有哪些性质呢?
C
A
B
D
对称性:
边:
角:
对角线:
中心对称图形
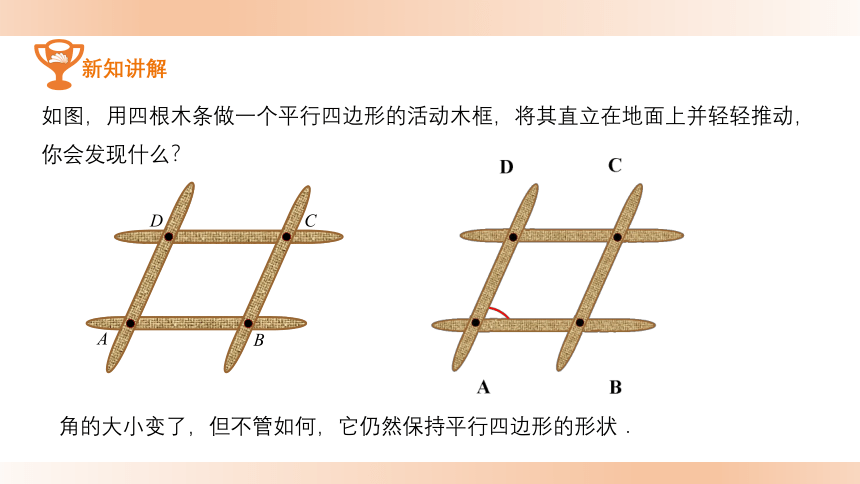
新知讲解
如图,用四根木条做一个平行四边形的活动木框,将其直立在地面上并轻轻推动,你会发现什么?
角的大小变了,但不管如何,它仍然保持平行四边形的形状.
D
A
C
B
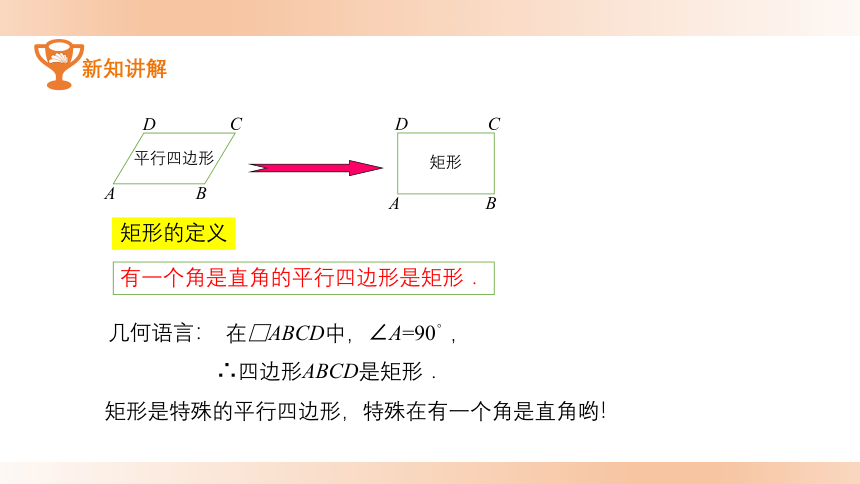
新知讲解
A
B
C
D
矩形是特殊的平行四边形,特殊在有一个角是直角哟!
A
B
C
D
有一个角是直角的平行四边形是矩形.
在□ABCD中,∠A=90。,
∴四边形ABCD是矩形.
平行四边形
矩形
矩形的定义
几何语言:
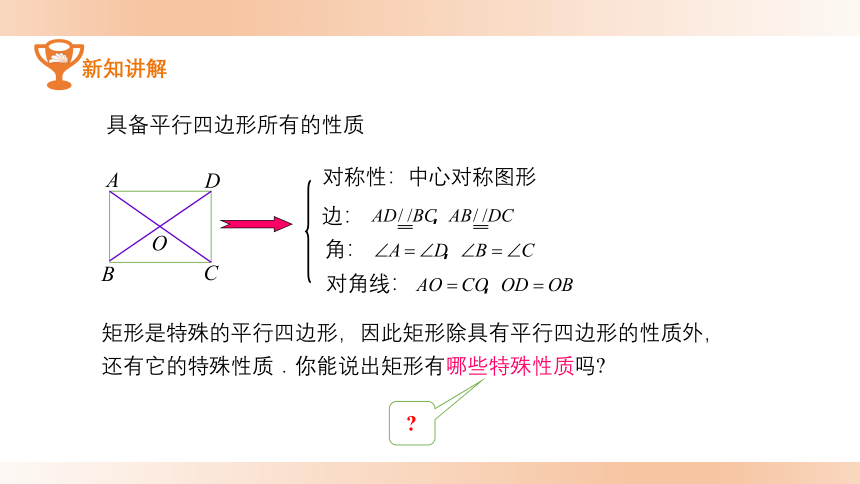
新知讲解
具备平行四边形所有的性质
A
B
C
D
O
对称性:
边:
角:
对角线:
中心对称图形
矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些特殊性质吗?
?
新知讲解
A
B
C
D
O
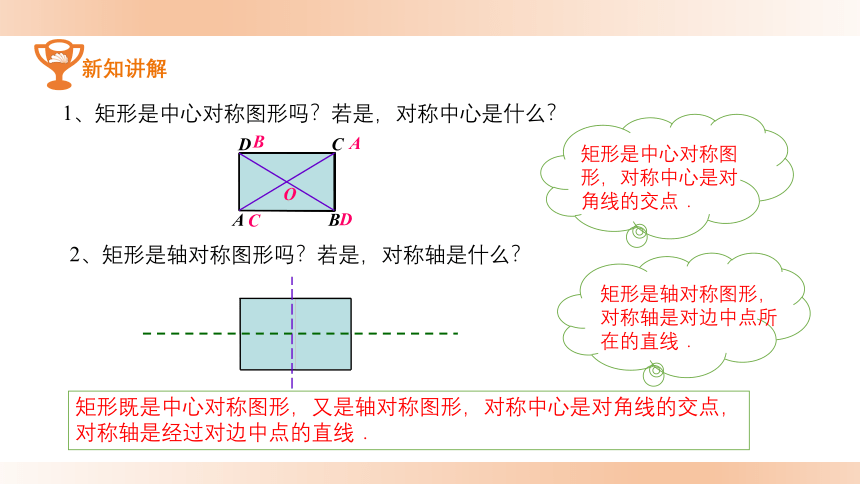
1、矩形是中心对称图形吗?若是,对称中心是什么?
2、矩形是轴对称图形吗?若是,对称轴是什么?
A
B
C
D
O
矩形既是中心对称图形,又是轴对称图形,对称中心是对角线的交点,对称轴是经过对边中点的直线.
矩形是中心对称图形,对称中心是对角线的交点.
矩形是轴对称图形,对称轴是对边中点所在的直线.
新知讲解
D
A
C
B
D
A
C
B
O
O
┓
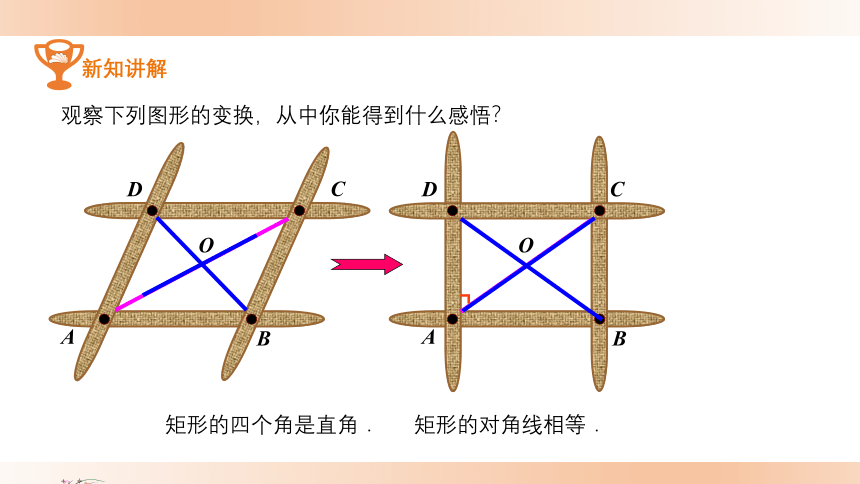
观察下列图形的变换,从中你能得到什么感悟?
矩形的四个角是直角.
矩形的对角线相等.
新知讲解
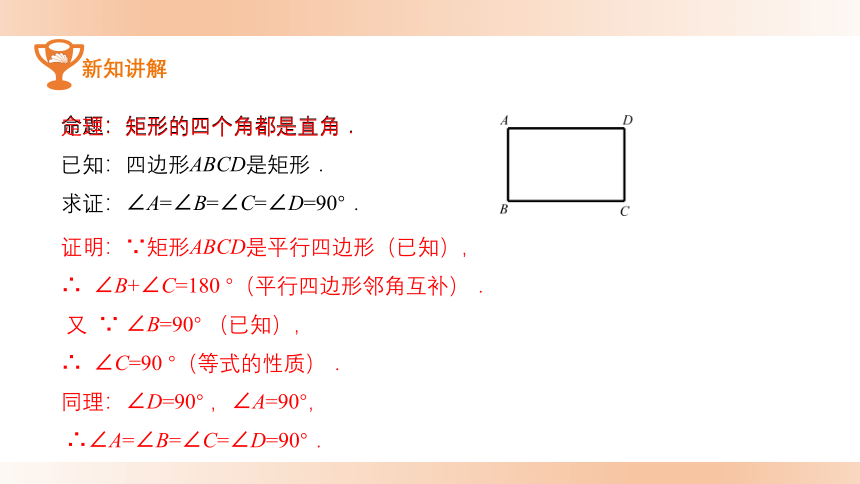
命题:矩形的四个角都是直角.
已知:四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
证明:∵矩形ABCD是平行四边形(已知),
∴ ∠B+∠C=180 °(平行四边形邻角互补).
又 ∵ ∠B=90° (已知),
∴ ∠C=90 °(等式的性质).
同理:∠D=90° ,∠A=90°,
∴∠A=∠B=∠C=∠D=90°.
定理:矩形的四个角都是直角.
新知讲解
命题:矩形的对角线相等.
已知:四边形ABCD是矩形.求证: AC = BD.
证明: ∵ABCD是矩形(已知),
∴∠ABC = ∠DAB = 90° ,BC = AD(矩形有性质).
在△ABC≌△BAD中
∵
∴△ABC≌△BAD(SAS),
∴AC = BD(对应边相等).
定理:矩形的对角线相等.
新知讲解
┒
邻边:
四个角都是直角
互相平分 AO=CO; BO=DO
(1)边:
(2)角:
(3)对角线:
对边:
(共性)
(共性)
(特性)
(特性)
(特性)
(共性)
A
B
C
D
O
平行 AD∥BC; AB∥CD
相等 AB=CD; AD=BC
相 等 AC=BD
互相垂直 AB⊥BC; AB⊥AD
A
B
D
C
O
∠BAD=∠ABC=∠BCD=∠CDA= 90°
┒
┒
┒
OA=OB=OC=OD=相等的对角线的一半.
对角相等、邻角互补
(共性)
新知讲解
{5940675A-B579-460E-94D1-54222C63F5DA}
边
角
对角线
对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
矩形所特有的性质
新知讲解
例1 如图,矩形ABCD被两条对角线分成四个小三角形,如果 四个小三角形周长的和是86 cm,矩形的对角线长是13 cm,那么该矩形的周长是多少?
解:∵△AOB、△BOC、△COD和△AOD四个小三角形周长的和为86 cm,
∴AB+BC+CD+DA+2(OA+OB+OC+OD)
=AB+BC+CD+DA+2(AC+BD)=86.
又∵AC=BD=13(矩形的对角线相等),
∴AB+BC+CD+DA=86-2(AC+BD)=86-4×13=34(cm),
即矩形ABCD的周长等于34 cm.
新知讲解
例2 如图,在矩形ABCD中,AB=3,BC=4,BE⊥AC,垂足为点E.
试求BE的长.
解:在矩形ABCD中,∠ABC=90°,
,
又∵ ,
∴ .
新知讲解
例3 如图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15 cm. 求AC、AB的长.
解:∵四边形ABCD是矩形,
∴AC=BD=15(矩形的对角线相等),
∴AO= AC=7.5,
∵AE垂直且平分BO,
∴AB=AO=7.5,
即AC的长为15 cm,AB的长为7.5 cm.
课堂练习
1、矩形具有而平行四边行不具有的的性质是( )
A.对角相等 B.对角线相等
C.对角线互相平分 D.对边平行且相等
2、矩形的一条对角线与一边的夹角为40°,则两条对角线相交所成的锐角是( )
A.20° B. 40° C.60° D.80°
3、已知一个矩形的长为4 cm,宽为3 cm,则其对角线长为________ .
4 、如图所示,矩形ABCD中,∠ABC的平分线交AD于点E.
若AB=6,DE=4,则矩形ABCD的周长是________ .
B
D
5 cm
32
课堂练习
5、如图,在矩形ABCD中,对角线AC、BD相交于点0,AB=2 cm,AC=4 cm.
(1)根据“矩形的对角线_____________”,可以得到BD=________cm;
(2)根据“矩形的对角线_____________”,可以得到AO=BO= AC=
_____cm,且AB=2cm,所以△AOB是_______三角形.
相等
4
互相平分
2
等边
课堂练习
6、如图,在矩形ABCD中,AB比AD的一半长2cm,AD=10cm,问△ABD的周长比△AOD的周长长多少?
解:∵四边形ABCD是正方形,
∴∠BAD=90°,OA=OB= BD,
∵AB比AD的一半长2cm,AD=10cm,
∴AB= AD+2cm=7cm,
∴△ABD的周长?△AOD的周长=(AB+AD+BD)?(OA+OB+AD)=AB=7cm.
课堂练习
7、如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4 cm,求矩形对角线的长.
解:∵ 四边形ABCD是矩形,
∴AC与BD相等且互相平分,
∴OA=OB.
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=AB=4 cm.
∴ 矩形的对角线长AC=BD=2OA=8 cm.
拓展提高
8、如图所示,在矩形ABCD中,对角线AC、BD相交于点O,CE//DB,交AD的延长线于点E.
(1)求证:四边形BCED为平行四边形;
(2)试说明:CE=2AO.
(1)证明:∵四边形ABCD是矩形,
∴AD//BC,AC=DB=2AO,
又∵CE//DB,
∴四边形BCED是平行四边形;
(2)证明:∵四边形BCED是平行四边形,
∴CE=BD,
由(1)得:DB=AC=2AO,
∴CE=2AO.
中考链接
1、 【2018·黑龙江】如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50° ,则∠ABE的度数为( )????
A.10° B.20° C.30° D.40°
2、【2018·四川】?矩形ABCD的对角线AC,BD相交于点O,若AB=AO,则∠ABD的度数是________.
60°
B
课堂总结
1、矩形的定义:
有一个角是直角的平行四边形是矩形.
2、矩形的性质:
(1)平行四边形的所有性质.
(2)矩形的四个角都是直角.
(3)矩形的对角线相等.
(4)矩形既是轴对称图形又是中心对称图形.
板书设计
有一个角是直角的平行四边形是矩形.
边:矩形对边平行且相等.
角:矩形的四个角都是直角.
对角线:矩形的对角线相等且平分.
对称性:矩形既是轴对称图形又是中
心对称图形.
例1
例2
例3
作业布置
教材第100页第2题、第3题,第101页第3题.
数学华师大版 八年级下
新知导入
1、什么是平行四边形?
两组对边分别平行的四边形是平行四边形.
2、平行四边形具有哪些性质呢?
C
A
B
D
对称性:
边:
角:
对角线:
中心对称图形
新知讲解
如图,用四根木条做一个平行四边形的活动木框,将其直立在地面上并轻轻推动,你会发现什么?
角的大小变了,但不管如何,它仍然保持平行四边形的形状.
D
A
C
B
新知讲解
A
B
C
D
矩形是特殊的平行四边形,特殊在有一个角是直角哟!
A
B
C
D
有一个角是直角的平行四边形是矩形.
在□ABCD中,∠A=90。,
∴四边形ABCD是矩形.
平行四边形
矩形
矩形的定义
几何语言:
新知讲解
具备平行四边形所有的性质
A
B
C
D
O
对称性:
边:
角:
对角线:
中心对称图形
矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些特殊性质吗?
?
新知讲解
A
B
C
D
O
1、矩形是中心对称图形吗?若是,对称中心是什么?
2、矩形是轴对称图形吗?若是,对称轴是什么?
A
B
C
D
O
矩形既是中心对称图形,又是轴对称图形,对称中心是对角线的交点,对称轴是经过对边中点的直线.
矩形是中心对称图形,对称中心是对角线的交点.
矩形是轴对称图形,对称轴是对边中点所在的直线.
新知讲解
D
A
C
B
D
A
C
B
O
O
┓
观察下列图形的变换,从中你能得到什么感悟?
矩形的四个角是直角.
矩形的对角线相等.
新知讲解
命题:矩形的四个角都是直角.
已知:四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
证明:∵矩形ABCD是平行四边形(已知),
∴ ∠B+∠C=180 °(平行四边形邻角互补).
又 ∵ ∠B=90° (已知),
∴ ∠C=90 °(等式的性质).
同理:∠D=90° ,∠A=90°,
∴∠A=∠B=∠C=∠D=90°.
定理:矩形的四个角都是直角.
新知讲解
命题:矩形的对角线相等.
已知:四边形ABCD是矩形.求证: AC = BD.
证明: ∵ABCD是矩形(已知),
∴∠ABC = ∠DAB = 90° ,BC = AD(矩形有性质).
在△ABC≌△BAD中
∵
∴△ABC≌△BAD(SAS),
∴AC = BD(对应边相等).
定理:矩形的对角线相等.
新知讲解
┒
邻边:
四个角都是直角
互相平分 AO=CO; BO=DO
(1)边:
(2)角:
(3)对角线:
对边:
(共性)
(共性)
(特性)
(特性)
(特性)
(共性)
A
B
C
D
O
平行 AD∥BC; AB∥CD
相等 AB=CD; AD=BC
相 等 AC=BD
互相垂直 AB⊥BC; AB⊥AD
A
B
D
C
O
∠BAD=∠ABC=∠BCD=∠CDA= 90°
┒
┒
┒
OA=OB=OC=OD=相等的对角线的一半.
对角相等、邻角互补
(共性)
新知讲解
{5940675A-B579-460E-94D1-54222C63F5DA}
边
角
对角线
对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
矩形所特有的性质
新知讲解
例1 如图,矩形ABCD被两条对角线分成四个小三角形,如果 四个小三角形周长的和是86 cm,矩形的对角线长是13 cm,那么该矩形的周长是多少?
解:∵△AOB、△BOC、△COD和△AOD四个小三角形周长的和为86 cm,
∴AB+BC+CD+DA+2(OA+OB+OC+OD)
=AB+BC+CD+DA+2(AC+BD)=86.
又∵AC=BD=13(矩形的对角线相等),
∴AB+BC+CD+DA=86-2(AC+BD)=86-4×13=34(cm),
即矩形ABCD的周长等于34 cm.
新知讲解
例2 如图,在矩形ABCD中,AB=3,BC=4,BE⊥AC,垂足为点E.
试求BE的长.
解:在矩形ABCD中,∠ABC=90°,
,
又∵ ,
∴ .
新知讲解
例3 如图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15 cm. 求AC、AB的长.
解:∵四边形ABCD是矩形,
∴AC=BD=15(矩形的对角线相等),
∴AO= AC=7.5,
∵AE垂直且平分BO,
∴AB=AO=7.5,
即AC的长为15 cm,AB的长为7.5 cm.
课堂练习
1、矩形具有而平行四边行不具有的的性质是( )
A.对角相等 B.对角线相等
C.对角线互相平分 D.对边平行且相等
2、矩形的一条对角线与一边的夹角为40°,则两条对角线相交所成的锐角是( )
A.20° B. 40° C.60° D.80°
3、已知一个矩形的长为4 cm,宽为3 cm,则其对角线长为________ .
4 、如图所示,矩形ABCD中,∠ABC的平分线交AD于点E.
若AB=6,DE=4,则矩形ABCD的周长是________ .
B
D
5 cm
32
课堂练习
5、如图,在矩形ABCD中,对角线AC、BD相交于点0,AB=2 cm,AC=4 cm.
(1)根据“矩形的对角线_____________”,可以得到BD=________cm;
(2)根据“矩形的对角线_____________”,可以得到AO=BO= AC=
_____cm,且AB=2cm,所以△AOB是_______三角形.
相等
4
互相平分
2
等边
课堂练习
6、如图,在矩形ABCD中,AB比AD的一半长2cm,AD=10cm,问△ABD的周长比△AOD的周长长多少?
解:∵四边形ABCD是正方形,
∴∠BAD=90°,OA=OB= BD,
∵AB比AD的一半长2cm,AD=10cm,
∴AB= AD+2cm=7cm,
∴△ABD的周长?△AOD的周长=(AB+AD+BD)?(OA+OB+AD)=AB=7cm.
课堂练习
7、如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4 cm,求矩形对角线的长.
解:∵ 四边形ABCD是矩形,
∴AC与BD相等且互相平分,
∴OA=OB.
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=AB=4 cm.
∴ 矩形的对角线长AC=BD=2OA=8 cm.
拓展提高
8、如图所示,在矩形ABCD中,对角线AC、BD相交于点O,CE//DB,交AD的延长线于点E.
(1)求证:四边形BCED为平行四边形;
(2)试说明:CE=2AO.
(1)证明:∵四边形ABCD是矩形,
∴AD//BC,AC=DB=2AO,
又∵CE//DB,
∴四边形BCED是平行四边形;
(2)证明:∵四边形BCED是平行四边形,
∴CE=BD,
由(1)得:DB=AC=2AO,
∴CE=2AO.
中考链接
1、 【2018·黑龙江】如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50° ,则∠ABE的度数为( )????
A.10° B.20° C.30° D.40°
2、【2018·四川】?矩形ABCD的对角线AC,BD相交于点O,若AB=AO,则∠ABD的度数是________.
60°
B
课堂总结
1、矩形的定义:
有一个角是直角的平行四边形是矩形.
2、矩形的性质:
(1)平行四边形的所有性质.
(2)矩形的四个角都是直角.
(3)矩形的对角线相等.
(4)矩形既是轴对称图形又是中心对称图形.
板书设计
有一个角是直角的平行四边形是矩形.
边:矩形对边平行且相等.
角:矩形的四个角都是直角.
对角线:矩形的对角线相等且平分.
对称性:矩形既是轴对称图形又是中
心对称图形.
例1
例2
例3
作业布置
教材第100页第2题、第3题,第101页第3题.
