华东师大版八年级下册20.3 数据的离散程度课件 (共32张PPT)
文档属性
| 名称 | 华东师大版八年级下册20.3 数据的离散程度课件 (共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 298.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 00:00:00 | ||
图片预览









文档简介
第20章 数据的整理与初步处理
20.3 数据的离散程度
问题一
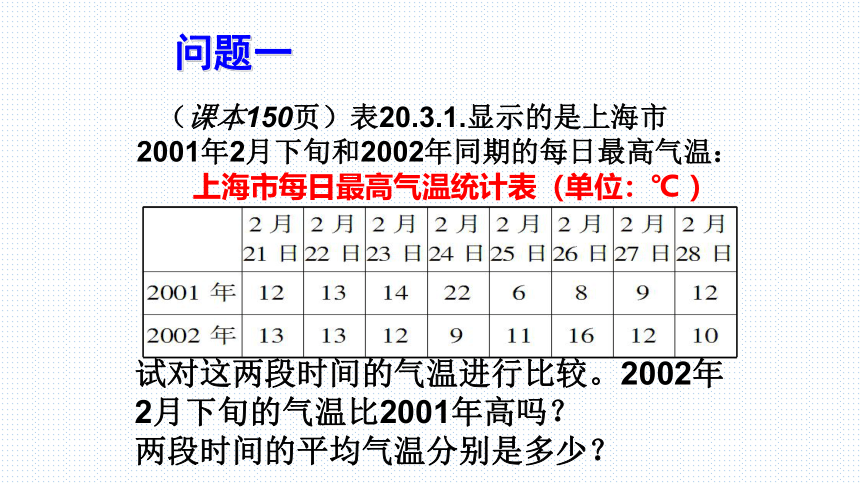
(课本150页)表20.3.1.显示的是上海市2001年2月下旬和2002年同期的每日最高气温:
上海市每日最高气温统计表(单位:℃ )
试对这两段时间的气温进行比较。2002年2月下旬的气温比2001年高吗?
两段时间的平均气温分别是多少?
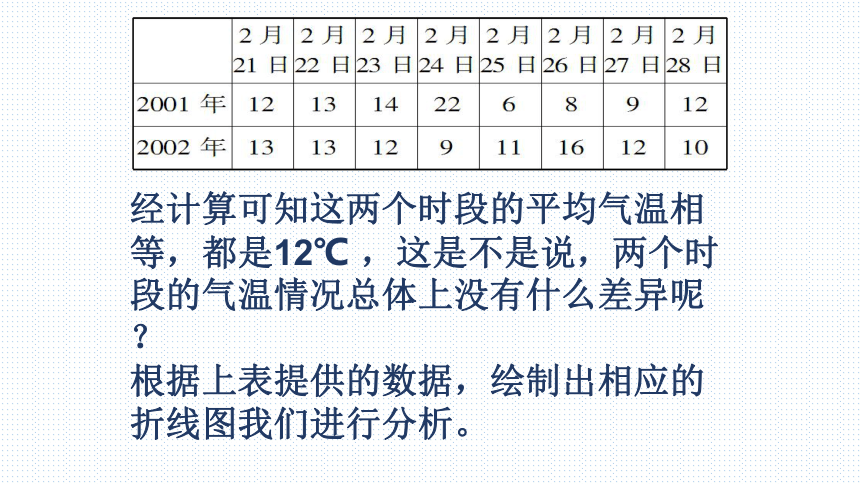
经计算可知这两个时段的平均气温相等,都是12℃ ,这是不是说,两个时段的气温情况总体上没有什么差异呢?
根据上表提供的数据,绘制出相应的折线图我们进行分析。
通过观察,发现:2001年2月下旬的气温波动较大——6℃到22℃,而2002年同期的气温波动较小——9℃到16℃ 。
什么样的指标可以反映一组数据变化范围的大小?
我们可以用一组数据中的最大值减去最小值所得的差来反映这组数据的变化范围。用这种方法得到的差称为极差。
思考
极差=最大值-最小值
问题:观察下图,分别说出两段时间内气温
的极差。
解:由图可知,图(a)中温度的最大值与最小值之间的差距很大,相差16℃,也就是极差为16℃;
图(b)中温度的最大值与最小值相差7℃,极差为 7℃,由此,我们可以判定2001年同期气温波动范围要大.
小明和小兵两人参加体育项目训练,近期的5次测试成绩如表所示,谁的成绩较为稳定?为什么?
问题二
通过计算,我们发现两人测试成绩的平均值都是12.4分。从表中可以看到:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}测试次数
1
2
3
4
5
小明
10
14
13
12
13
小兵
11
11
15
14
11
相比之下,小明的成绩大部分集中在12.4分附近,
而小兵的成绩与其平均值的离散程度较大。
如果一组数据与其平均值的离散程度较小,我们就说它比较稳定。
所以我们说小明的成绩比较稳定
思考
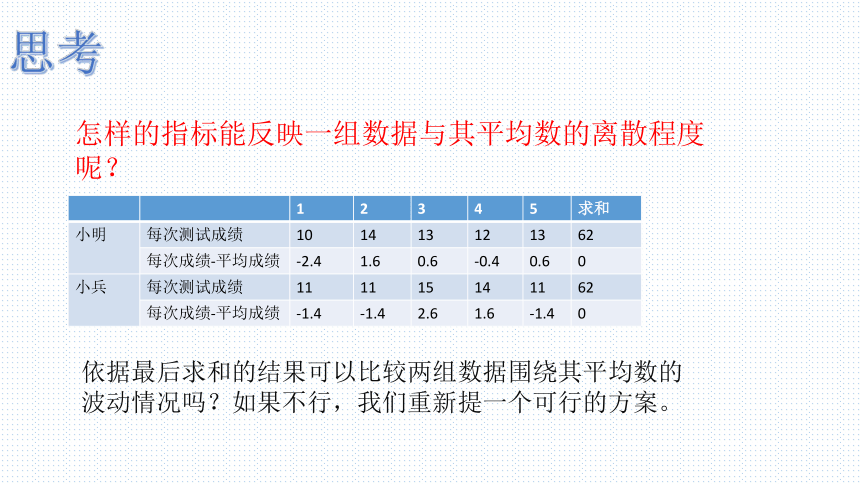
怎样的指标能反映一组数据与其平均数的离散程度呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
3
4
5
求和
小明
每次测试成绩
10
14
13
12
13
62
每次成绩-平均成绩
-2.4
1.6
0.6
-0.4
0.6
0
小兵
每次测试成绩
11
11
15
14
11
62
每次成绩-平均成绩
-1.4
-1.4
2.6
1.6
-1.4
0
依据最后求和的结果可以比较两组数据围绕其平均数的波动情况吗?如果不行,我们重新提一个可行的方案。
【归纳结论】我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况,这个结果称为方差.
我们通常用s2表示一组数据的方差,用 表示一组数据的平均数,x1、x2、…、xn表示各个数据,方差的计算公式:
例题.甲、乙两种水稻试验品种连续5年的平均单位面积产量(单位:t/m2)如下:
经计算,x甲=10,x乙=10,试根据这组数据估计哪个水稻品种的产量比较稳定?
第1年
第2年
第3年
第4年
第5年
甲
9.8
9.9
10.1
10
10.2
乙
9.4
10.3
10.8
9.7
9.8
A
B
3.若一组数据2,4,x,6,8的平均数是5,则这组数据的方差是________.
4
4.为了比较甲、乙两种水稻秧苗是否出苗整齐,每种秧苗各取10株分别量出每株长度,发现两组秧苗的平均长度一样,甲、乙两种水稻秧苗的方差分别是3.9,15.8,则下列说法正确的是( )
A.甲秧苗出苗更整齐
B.乙秧苗出苗更整齐
C.甲、乙秧苗出苗一样整齐
D.无法确定
A
B
7.某校为了选拔学生参加我市2017年无线电测试比赛中的装机比赛,教练对甲、乙两选手平时五次训练成绩进行统计,两选手五次训练的平均成绩均为30分钟,方差分别是s甲2=51,s乙2=12.则甲、乙两选手成绩比较稳定的是__________.
乙
8.工厂欲招收一名技工,下表是对三名应聘者加工相同数量同一种零件的数据进行分析所得的结果,你认为录用哪位较好?( )
A.甲 B.乙
C.丙 D.无法判断
C
甲
乙
丙
平均数
80
85
85
方差
86
92
86
9.(2017·烟台)甲、乙两地去年12月前5天的日平均气温如图所示,下列描述错误的是( )
A.两地气温的平均数相同
B.甲地气温的中位数是6 ℃
C.乙地气温的众数是4 ℃
D.乙地气温相对比较稳定
C
10.甲、乙、丙三台包装机同时分装质量为400克的茶叶,从它们各自分装的茶叶中分别随机抽取了10盒,测得它们的实际质量的方差如下表所示:
根据表中数据,可以认为三台包装机中, ____包装机包装的茶叶质量最稳定.
乙
解:乙包装机包装的茶叶质量最稳定.
11.某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛,抽查了两人在最近10次选拔赛中的成绩(单位:cm)如下:
甲:585 596 610 598 612 597 604 600 613 601
乙:613 618 580 574 618 593 585 590 598 624
你认为该派谁参加?
解析:此题可从平均数,方差两方面去分析.当平均数相差不大时,再看方差.
知识点3:用计算器求方差
11.用计算器求得一组数据:71,95,63,82,90,77,86,93,97,86的方差为( )
A.53.9 B.84.2 C.107.8 D.124.5
C
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
课堂小结
这节课你有哪些收获?
课堂演练
1.正确的是( )
A.两组数据,平均数越大,波动越大
B.两组数据,中位数越大,波动越大
C.两组数据,方差越大,波动越大
D.两组数据的波动大小由平均数、方差共同说明
C
易错点:未弄清方差的概念及计算公式造成错解
2.(导学号19414146)(2017·泰州)某科普小组有5名成员,身高分别为(单位:cm):160,165,170,163,167.增加1名身高为165 cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是( )
A.平均数不变,方差不变 B.平均数不变,方差变大
C.平均数不变,方差变小 D.平均数变小,方差不变
C
3.如图是小强同学根据乐山城区某天上午和下午四个整时的气温绘制成的折线图.请你回答:该天上午和下午的气温哪个更稳定?
答:________;理由是_______________________________________
__________________________________.
下午
因为上午气温和下午气温的平均数相同,
上午气温的方差大于下午气温的方差
5.某校准备从甲、乙两名优秀选手中选1名参加全市中学生田径百米比赛,该校预先对这两名选手测试8次,测试成绩(单位:s)如下表所示:
根据测试成绩,请你运用所学的统计知识作出判断,选哪一名选手参加比赛更好,为什么?
1
2
3
4
5
6
7
8
甲的
成绩
12.1
12.2
13
12.5
13.1
12.5
12.4
12.2
乙的
成绩
12
12.4
12.8
13
12.2
12.8
12.3
12.5
20.3 数据的离散程度
问题一
(课本150页)表20.3.1.显示的是上海市2001年2月下旬和2002年同期的每日最高气温:
上海市每日最高气温统计表(单位:℃ )
试对这两段时间的气温进行比较。2002年2月下旬的气温比2001年高吗?
两段时间的平均气温分别是多少?
经计算可知这两个时段的平均气温相等,都是12℃ ,这是不是说,两个时段的气温情况总体上没有什么差异呢?
根据上表提供的数据,绘制出相应的折线图我们进行分析。
通过观察,发现:2001年2月下旬的气温波动较大——6℃到22℃,而2002年同期的气温波动较小——9℃到16℃ 。
什么样的指标可以反映一组数据变化范围的大小?
我们可以用一组数据中的最大值减去最小值所得的差来反映这组数据的变化范围。用这种方法得到的差称为极差。
思考
极差=最大值-最小值
问题:观察下图,分别说出两段时间内气温
的极差。
解:由图可知,图(a)中温度的最大值与最小值之间的差距很大,相差16℃,也就是极差为16℃;
图(b)中温度的最大值与最小值相差7℃,极差为 7℃,由此,我们可以判定2001年同期气温波动范围要大.
小明和小兵两人参加体育项目训练,近期的5次测试成绩如表所示,谁的成绩较为稳定?为什么?
问题二
通过计算,我们发现两人测试成绩的平均值都是12.4分。从表中可以看到:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}测试次数
1
2
3
4
5
小明
10
14
13
12
13
小兵
11
11
15
14
11
相比之下,小明的成绩大部分集中在12.4分附近,
而小兵的成绩与其平均值的离散程度较大。
如果一组数据与其平均值的离散程度较小,我们就说它比较稳定。
所以我们说小明的成绩比较稳定
思考
怎样的指标能反映一组数据与其平均数的离散程度呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
3
4
5
求和
小明
每次测试成绩
10
14
13
12
13
62
每次成绩-平均成绩
-2.4
1.6
0.6
-0.4
0.6
0
小兵
每次测试成绩
11
11
15
14
11
62
每次成绩-平均成绩
-1.4
-1.4
2.6
1.6
-1.4
0
依据最后求和的结果可以比较两组数据围绕其平均数的波动情况吗?如果不行,我们重新提一个可行的方案。
【归纳结论】我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况,这个结果称为方差.
我们通常用s2表示一组数据的方差,用 表示一组数据的平均数,x1、x2、…、xn表示各个数据,方差的计算公式:
例题.甲、乙两种水稻试验品种连续5年的平均单位面积产量(单位:t/m2)如下:
经计算,x甲=10,x乙=10,试根据这组数据估计哪个水稻品种的产量比较稳定?
第1年
第2年
第3年
第4年
第5年
甲
9.8
9.9
10.1
10
10.2
乙
9.4
10.3
10.8
9.7
9.8
A
B
3.若一组数据2,4,x,6,8的平均数是5,则这组数据的方差是________.
4
4.为了比较甲、乙两种水稻秧苗是否出苗整齐,每种秧苗各取10株分别量出每株长度,发现两组秧苗的平均长度一样,甲、乙两种水稻秧苗的方差分别是3.9,15.8,则下列说法正确的是( )
A.甲秧苗出苗更整齐
B.乙秧苗出苗更整齐
C.甲、乙秧苗出苗一样整齐
D.无法确定
A
B
7.某校为了选拔学生参加我市2017年无线电测试比赛中的装机比赛,教练对甲、乙两选手平时五次训练成绩进行统计,两选手五次训练的平均成绩均为30分钟,方差分别是s甲2=51,s乙2=12.则甲、乙两选手成绩比较稳定的是__________.
乙
8.工厂欲招收一名技工,下表是对三名应聘者加工相同数量同一种零件的数据进行分析所得的结果,你认为录用哪位较好?( )
A.甲 B.乙
C.丙 D.无法判断
C
甲
乙
丙
平均数
80
85
85
方差
86
92
86
9.(2017·烟台)甲、乙两地去年12月前5天的日平均气温如图所示,下列描述错误的是( )
A.两地气温的平均数相同
B.甲地气温的中位数是6 ℃
C.乙地气温的众数是4 ℃
D.乙地气温相对比较稳定
C
10.甲、乙、丙三台包装机同时分装质量为400克的茶叶,从它们各自分装的茶叶中分别随机抽取了10盒,测得它们的实际质量的方差如下表所示:
根据表中数据,可以认为三台包装机中, ____包装机包装的茶叶质量最稳定.
乙
解:乙包装机包装的茶叶质量最稳定.
11.某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛,抽查了两人在最近10次选拔赛中的成绩(单位:cm)如下:
甲:585 596 610 598 612 597 604 600 613 601
乙:613 618 580 574 618 593 585 590 598 624
你认为该派谁参加?
解析:此题可从平均数,方差两方面去分析.当平均数相差不大时,再看方差.
知识点3:用计算器求方差
11.用计算器求得一组数据:71,95,63,82,90,77,86,93,97,86的方差为( )
A.53.9 B.84.2 C.107.8 D.124.5
C
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
课堂小结
这节课你有哪些收获?
课堂演练
1.正确的是( )
A.两组数据,平均数越大,波动越大
B.两组数据,中位数越大,波动越大
C.两组数据,方差越大,波动越大
D.两组数据的波动大小由平均数、方差共同说明
C
易错点:未弄清方差的概念及计算公式造成错解
2.(导学号19414146)(2017·泰州)某科普小组有5名成员,身高分别为(单位:cm):160,165,170,163,167.增加1名身高为165 cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是( )
A.平均数不变,方差不变 B.平均数不变,方差变大
C.平均数不变,方差变小 D.平均数变小,方差不变
C
3.如图是小强同学根据乐山城区某天上午和下午四个整时的气温绘制成的折线图.请你回答:该天上午和下午的气温哪个更稳定?
答:________;理由是_______________________________________
__________________________________.
下午
因为上午气温和下午气温的平均数相同,
上午气温的方差大于下午气温的方差
5.某校准备从甲、乙两名优秀选手中选1名参加全市中学生田径百米比赛,该校预先对这两名选手测试8次,测试成绩(单位:s)如下表所示:
根据测试成绩,请你运用所学的统计知识作出判断,选哪一名选手参加比赛更好,为什么?
1
2
3
4
5
6
7
8
甲的
成绩
12.1
12.2
13
12.5
13.1
12.5
12.4
12.2
乙的
成绩
12
12.4
12.8
13
12.2
12.8
12.3
12.5
