华东师大版八年级下册课件:19.2.2 菱形的判定(共26张PPT)
文档属性
| 名称 | 华东师大版八年级下册课件:19.2.2 菱形的判定(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 17:05:11 | ||
图片预览




文档简介
菱形的判定
数学华师大版 八年级下
新知导入
取两根长度不等的细纸条,将两根纸条的中点重合并固定在一起,用笔和直尺画出纸条四个端点的连线,则这四条线段组成一个什么图形,若转动其中一根纸条,使两根纸条之间的夹角等于 90° ,请猜想这时图形的形状是什么图形?
新知讲解
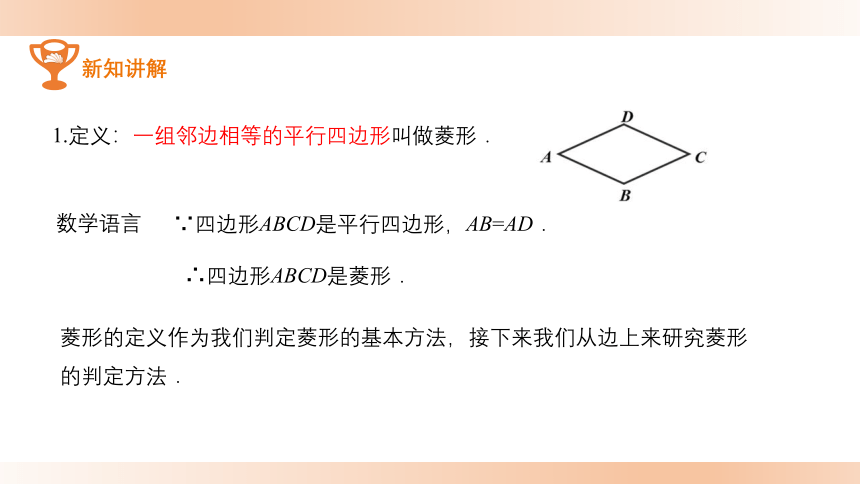
1.定义:一组邻边相等的平行四边形叫做菱形.
菱形的定义作为我们判定菱形的基本方法,接下来我们从边上来研究菱形的判定方法.
∵四边形ABCD是平行四边形,AB=AD.
∴四边形ABCD是菱形.
数学语言
新知讲解
四条边相等的四边形是菱形.
菱形的四条边相等.
逆命题
这个逆命题成立吗?
新知讲解
作一个四条边都相等的四边形.
步骤:
1.画两条相等的线段AB、CD;
2.分别以点B和点D为圆心,AB长为半径画弧,两弧相交于点C;
3.连结BC、CD,即得一个四条边都相等的四边形ABCD.
这个四边形是菱形吗?
新知讲解
命题:四条边相等的四边形是菱形.
已知:在四边形ABCD中, AB=BC=CD=DA.
求证:四边形ABCD是菱形.
证明:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
又∵AB=AD,
∴四边形ABCD是菱形.
定理:四条边相等的四边形是菱形.
菱形判定定理1
新知讲解
有三条边相等的四边形是菱形吗?请同学动手画一画,你发现什么结论?
结论:有三条边相等的四边形不是菱形.
新知讲解
数学语言:
在四边形ABCD中,
∵ AB=BC=CD=DA,
∴四边形ABCD是菱形.
菱形的判定1:
四条边都相等的四边形是菱形.
新知讲解
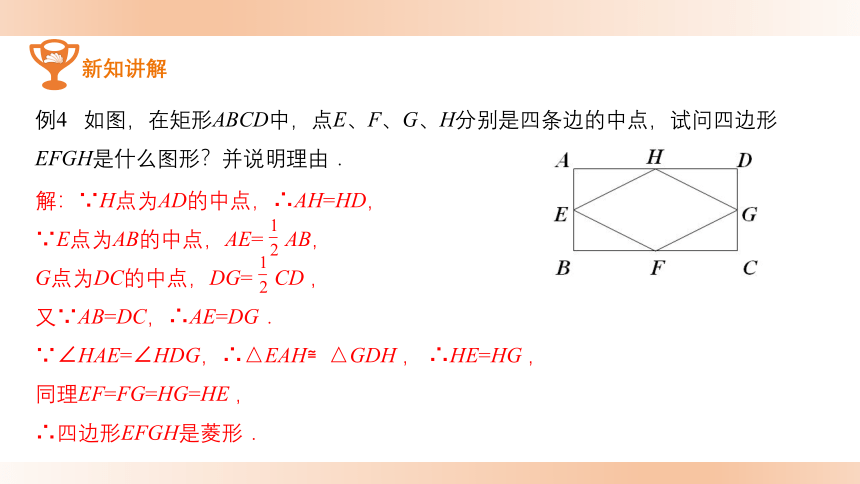
例4 如图,在矩形ABCD中,点E、F、G、H分别是四条边的中点,试问四边形EFGH是什么图形?并说明理由.
解:∵H点为AD的中点,∴AH=HD,
∵E点为AB的中点,AE= AB,
G点为DC的中点,DG= CD ,
又∵AB=DC,∴AE=DG.
∵∠HAE=∠HDG,∴△EAH≌△GDH , ∴HE=HG ,
同理EF=FG=HG=HE ,
∴四边形EFGH是菱形.
新知讲解
若四边形ABCD的对角线AC⊥BD,则四边形ABCD是不是菱形?
结论:对角线互相垂直的四边形不能判定为菱形.
对角线互相垂直的平形四边形是菱形吗?
新知讲解
作一个两条对角线互相垂直的平行四边形.
步骤:
1.作两条互相垂直的直线m,n,记交点为点O;
2.以点O为圆心,适当长为半径画弧,在直线m上截取相等的两条线段OA、OC;
3.以点O为圆心,另一适当长为半径画弧,在直线n上截取相等的两条线段OB、OD;
4.顺次连结所行的四点,即得一个对角线互相垂直且平分的四边形ABCD,显然,它是一个对角线互相垂直的平行四边形.
这个平行四边形是菱形吗?
新知讲解
命题:对角线互相垂直的平行四边形是菱形.
已知:在平行四边形ABCD中,AC⊥BD .
求证:平行四边形ABCD是菱形.
证明:∵四边形ABCD是平行四边形,
∴OA=OC.
又∵AC⊥BD,
∴BA=BC,
∴ 平行四边形ABCD是菱形.(有一组邻边相等的平行四边形是菱形)
定理:对角线互相垂直的平行四边形是菱形.
新知讲解
数学语言:∵在□ABCD中,AC⊥BD,
∴ □ABCD是菱形.
菱形的判定2:对角线互相垂直的平行四边形是菱形.
平行四边形ABCD
AC⊥BD
菱形ABCD
新知讲解
取两根长度不等的细纸条,将两根纸条的中点重合并固定在一起,用笔和直尺画出纸条四个端点的连线,则这四条线段组成一个什么图形,若转动其中一根纸条,使两根纸条之间的夹角等于 90° ,请猜想这时图形的形状是什么图形?
这四条线段组成平行四边形,
理由:对角线互相平分的四边形是平行四边形.
当两根纸条之间的夹角等于 90° 时,这时图形是菱形,
理由:对角线互相垂直的平行四边形是菱形.
新知讲解
例5 如图,已知矩形ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F.
求证:四边形AFCE是菱形.
分析:要证四边形AFCE是菱形,由已知条件可知EF⊥AC,所以只需证明四边形AFCE是平行四边形,又知EF垂直平分AC,所以只需证明OE=OF.
新知讲解
证明:∵四边形ABCD是矩形,
∴AE∥FC,
∴ ∠1=∠2,
∵EF平分AC,
∴OA=OC.
又∵ ∠AOE=∠COF=90°,
∴ △AOE≌△COF.
∴ 四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).
1. 判断题
(1)对角线互相垂直的四边形是菱形( )
(2)一条对角线垂直另一条对角线的四边形是菱形( )
(3)对角线互相垂直且平分的四边形是菱形( )
(4)对角线相等的四边形是菱形( )
(5)对角线互相平分且邻边相等的四边形是菱形( )
(6)两组对边分别平行且一组邻边相等的四边形是菱形( )
课堂练习
×
√
×
×
√
√
课堂练习
2. □ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形.
菱
矩
矩
菱
课堂练习
3. 下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
4. 对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形 C.菱形 D.以上都不对
5. 下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分 B.AB=BC,AD=CD,且AC⊥BD
C.AB=BC=CD=DA D.AB=CD,AD=BC,AC⊥BD
C
C
B
课堂练习
6、如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
证明:四边形ADCE是菱形.
证明:∵∠ACB=90°,D为AB的中点,
∴AD=CD=BD.
∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形且AD=CD,
∴四边形ADCE是菱形.
拓展提高
7、如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
拓展提高
(1)证明:∵AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AD=AB,
∵BA=BC,
∴AD=BC,
∴四边形ABCD是平行四边形,
∵BA=BC,
∴四边形ABCD是菱形;
(2)解:∵DE⊥BD,∴∠BDE=90°,
∴∠DBC+∠E=∠BDC+∠CDE=90°,
∵CB=CD,∴∠DBC=∠BDC,
∴∠CDE=∠E,
∴CD=CE=BC,
∴BE=2BC=10,
∵BD=8,
∴DE= =6,
∵四边形ABCD是菱形,
∴AD=AB=BC=5,
∴四边形ABED的周长=AD+AB+BE+DE=26.
中考链接
【2018?四川】如图,在?ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD//BC,
∵DE=BF,
∴AE=CF,∵AE//CF,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴四边形AECF是菱形.
课堂总结
有一组邻边相等的平行四边形叫做菱形.
对角线互相垂直的平行四边形是菱形.
有四条边相等的四边形是菱形.
+ 邻边相等 =
+对角线线互相垂直 =
四条边相等 + =
菱形的判定方法
板书设计
菱形的判定方法:
有一组邻边相等的平行四边形叫做菱形.
有四条边相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
例4
例5
作业布置
教材118页,第2题、第3题、第4题.
数学华师大版 八年级下
新知导入
取两根长度不等的细纸条,将两根纸条的中点重合并固定在一起,用笔和直尺画出纸条四个端点的连线,则这四条线段组成一个什么图形,若转动其中一根纸条,使两根纸条之间的夹角等于 90° ,请猜想这时图形的形状是什么图形?
新知讲解
1.定义:一组邻边相等的平行四边形叫做菱形.
菱形的定义作为我们判定菱形的基本方法,接下来我们从边上来研究菱形的判定方法.
∵四边形ABCD是平行四边形,AB=AD.
∴四边形ABCD是菱形.
数学语言
新知讲解
四条边相等的四边形是菱形.
菱形的四条边相等.
逆命题
这个逆命题成立吗?
新知讲解
作一个四条边都相等的四边形.
步骤:
1.画两条相等的线段AB、CD;
2.分别以点B和点D为圆心,AB长为半径画弧,两弧相交于点C;
3.连结BC、CD,即得一个四条边都相等的四边形ABCD.
这个四边形是菱形吗?
新知讲解
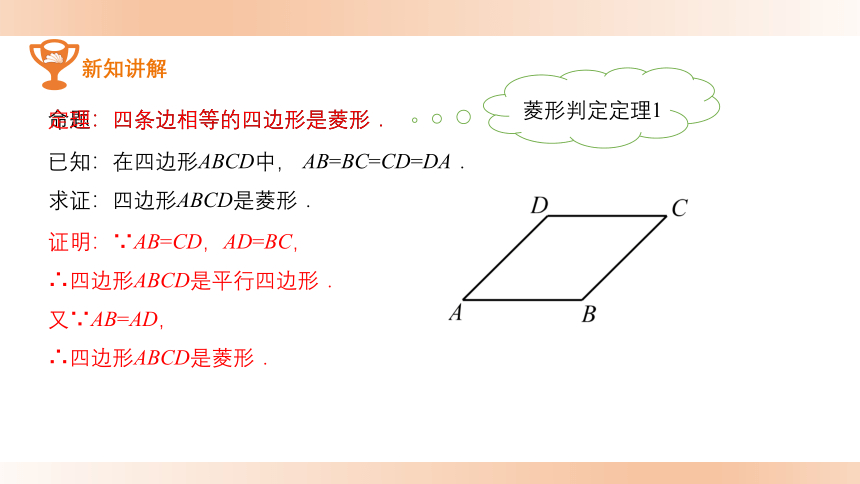
命题:四条边相等的四边形是菱形.
已知:在四边形ABCD中, AB=BC=CD=DA.
求证:四边形ABCD是菱形.
证明:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
又∵AB=AD,
∴四边形ABCD是菱形.
定理:四条边相等的四边形是菱形.
菱形判定定理1
新知讲解
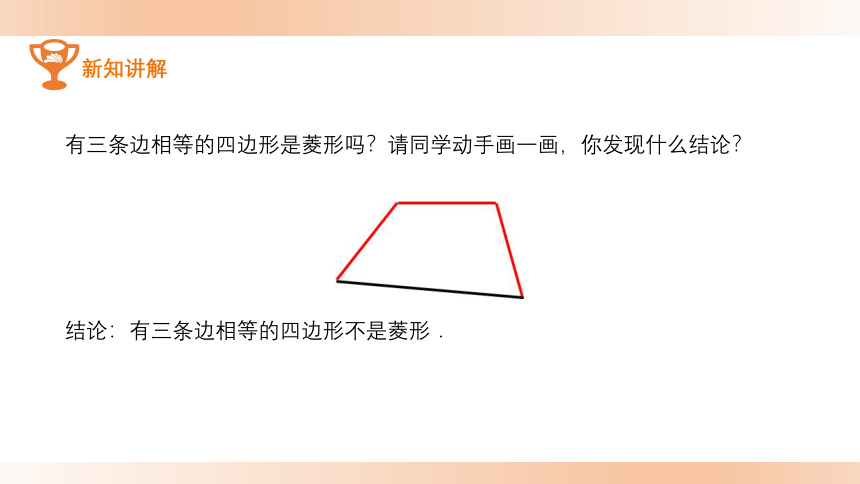
有三条边相等的四边形是菱形吗?请同学动手画一画,你发现什么结论?
结论:有三条边相等的四边形不是菱形.
新知讲解
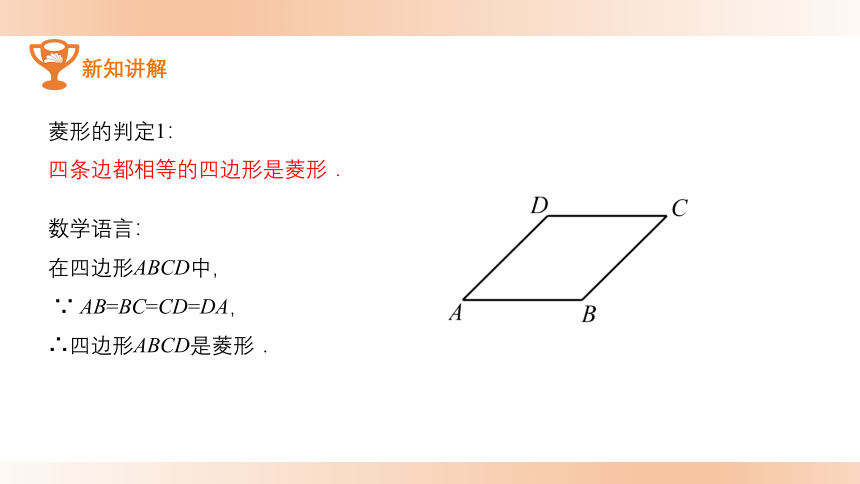
数学语言:
在四边形ABCD中,
∵ AB=BC=CD=DA,
∴四边形ABCD是菱形.
菱形的判定1:
四条边都相等的四边形是菱形.
新知讲解
例4 如图,在矩形ABCD中,点E、F、G、H分别是四条边的中点,试问四边形EFGH是什么图形?并说明理由.
解:∵H点为AD的中点,∴AH=HD,
∵E点为AB的中点,AE= AB,
G点为DC的中点,DG= CD ,
又∵AB=DC,∴AE=DG.
∵∠HAE=∠HDG,∴△EAH≌△GDH , ∴HE=HG ,
同理EF=FG=HG=HE ,
∴四边形EFGH是菱形.
新知讲解
若四边形ABCD的对角线AC⊥BD,则四边形ABCD是不是菱形?
结论:对角线互相垂直的四边形不能判定为菱形.
对角线互相垂直的平形四边形是菱形吗?
新知讲解
作一个两条对角线互相垂直的平行四边形.
步骤:
1.作两条互相垂直的直线m,n,记交点为点O;
2.以点O为圆心,适当长为半径画弧,在直线m上截取相等的两条线段OA、OC;
3.以点O为圆心,另一适当长为半径画弧,在直线n上截取相等的两条线段OB、OD;
4.顺次连结所行的四点,即得一个对角线互相垂直且平分的四边形ABCD,显然,它是一个对角线互相垂直的平行四边形.
这个平行四边形是菱形吗?
新知讲解
命题:对角线互相垂直的平行四边形是菱形.
已知:在平行四边形ABCD中,AC⊥BD .
求证:平行四边形ABCD是菱形.
证明:∵四边形ABCD是平行四边形,
∴OA=OC.
又∵AC⊥BD,
∴BA=BC,
∴ 平行四边形ABCD是菱形.(有一组邻边相等的平行四边形是菱形)
定理:对角线互相垂直的平行四边形是菱形.
新知讲解
数学语言:∵在□ABCD中,AC⊥BD,
∴ □ABCD是菱形.
菱形的判定2:对角线互相垂直的平行四边形是菱形.
平行四边形ABCD
AC⊥BD
菱形ABCD
新知讲解
取两根长度不等的细纸条,将两根纸条的中点重合并固定在一起,用笔和直尺画出纸条四个端点的连线,则这四条线段组成一个什么图形,若转动其中一根纸条,使两根纸条之间的夹角等于 90° ,请猜想这时图形的形状是什么图形?
这四条线段组成平行四边形,
理由:对角线互相平分的四边形是平行四边形.
当两根纸条之间的夹角等于 90° 时,这时图形是菱形,
理由:对角线互相垂直的平行四边形是菱形.
新知讲解
例5 如图,已知矩形ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F.
求证:四边形AFCE是菱形.
分析:要证四边形AFCE是菱形,由已知条件可知EF⊥AC,所以只需证明四边形AFCE是平行四边形,又知EF垂直平分AC,所以只需证明OE=OF.
新知讲解
证明:∵四边形ABCD是矩形,
∴AE∥FC,
∴ ∠1=∠2,
∵EF平分AC,
∴OA=OC.
又∵ ∠AOE=∠COF=90°,
∴ △AOE≌△COF.
∴ 四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).
1. 判断题
(1)对角线互相垂直的四边形是菱形( )
(2)一条对角线垂直另一条对角线的四边形是菱形( )
(3)对角线互相垂直且平分的四边形是菱形( )
(4)对角线相等的四边形是菱形( )
(5)对角线互相平分且邻边相等的四边形是菱形( )
(6)两组对边分别平行且一组邻边相等的四边形是菱形( )
课堂练习
×
√
×
×
√
√
课堂练习
2. □ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形.
菱
矩
矩
菱
课堂练习
3. 下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
4. 对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形 C.菱形 D.以上都不对
5. 下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分 B.AB=BC,AD=CD,且AC⊥BD
C.AB=BC=CD=DA D.AB=CD,AD=BC,AC⊥BD
C
C
B
课堂练习
6、如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
证明:四边形ADCE是菱形.
证明:∵∠ACB=90°,D为AB的中点,
∴AD=CD=BD.
∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形且AD=CD,
∴四边形ADCE是菱形.
拓展提高
7、如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
拓展提高
(1)证明:∵AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AD=AB,
∵BA=BC,
∴AD=BC,
∴四边形ABCD是平行四边形,
∵BA=BC,
∴四边形ABCD是菱形;
(2)解:∵DE⊥BD,∴∠BDE=90°,
∴∠DBC+∠E=∠BDC+∠CDE=90°,
∵CB=CD,∴∠DBC=∠BDC,
∴∠CDE=∠E,
∴CD=CE=BC,
∴BE=2BC=10,
∵BD=8,
∴DE= =6,
∵四边形ABCD是菱形,
∴AD=AB=BC=5,
∴四边形ABED的周长=AD+AB+BE+DE=26.
中考链接
【2018?四川】如图,在?ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD//BC,
∵DE=BF,
∴AE=CF,∵AE//CF,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴四边形AECF是菱形.
课堂总结
有一组邻边相等的平行四边形叫做菱形.
对角线互相垂直的平行四边形是菱形.
有四条边相等的四边形是菱形.
+ 邻边相等 =
+对角线线互相垂直 =
四条边相等 + =
菱形的判定方法
板书设计
菱形的判定方法:
有一组邻边相等的平行四边形叫做菱形.
有四条边相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
例4
例5
作业布置
教材118页,第2题、第3题、第4题.
