华东师大版八年级下册数学 19.3 正方形的性质(共21张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 19.3 正方形的性质(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 887.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 17:08:13 | ||
图片预览








文档简介
19.3 正方形的性质和判定定理
义务教育教科书 数学 八年级 下册
理解正方形的概念以及正方形、菱形、矩形、平行四边形之间的关系.
掌握正方形的性质与判定,并能运
用它们进行证明和计算.
1
学习目标
2
矩形的定义.
菱形的定义.
复习回顾
1.类比矩形和菱形的定义,说说正方形的定义.
新知探究
定义:有一组邻边相等,并且有一个角是直角的
平行四边形叫做正方形.
1.类比矩形和菱形的定义,说说正方形的定义.
正方形是矩形吗?
正方形是菱形吗?
正方形既是矩形又是菱形.
新知新究
{BDBED569-4797-4DF1-A0F4-6AAB3CD982D8}
边
角
对角线
对称性
文字
语言
符号
语言
对边平行,
四条边都相等
四个角都是直角
对角线相等且互相
垂直平分,每条对
角线平分一组对角
是轴对称图形,有四条对称轴
∵四边形ABCD
是正方形,
∴AB∥CD,
AD∥BC,
AB =BC =CD =DA.
∵四边形ABCD
是正方形,
∴∠DAB =∠ABC
=∠BCD =∠ADC
=90°.
∵四边形ABCD
是正方形,
∴AC =BD,AC⊥BD,
OA =OC =OB =OD,
∠DAC =∠BAC,
∠DCA =∠BCA,
∠ADB =∠CDB,
∠ABD =∠CBD.
正方形的性质
2.正方形有哪些性质?
新知探究
证明:∵四边形ABCD 是正方形,
∴AC⊥BD,AO=BO=CO=DO.
∴△ABO,△BCO,△CDO,△DAO 都是
等腰直角三角形,并且
△ABO ≌△BCO ≌△CDO ≌△DAO .
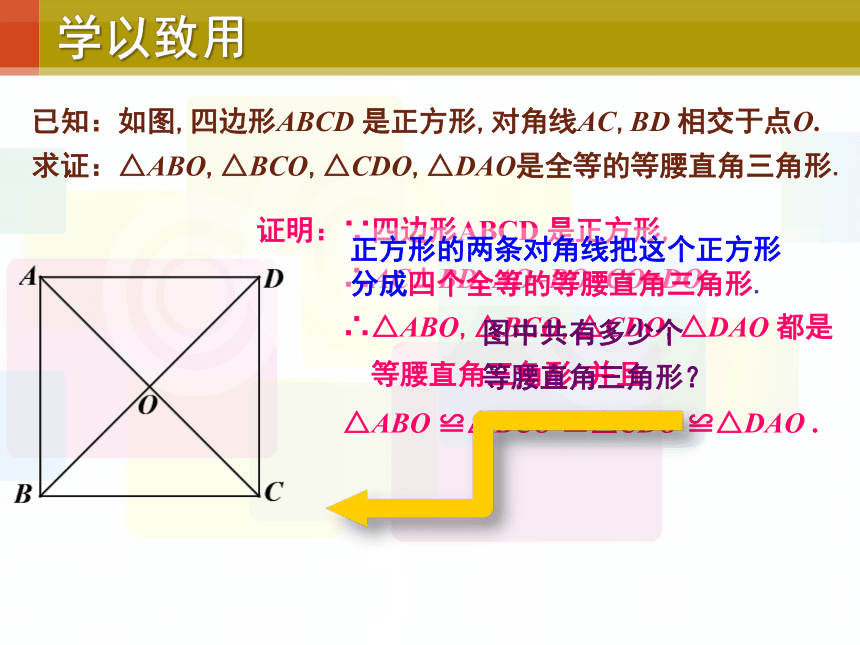
已知:如图,四边形ABCD 是正方形,对角线AC,BD 相交于点O.
求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三角形.
正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
图中共有多少个
等腰直角三角形?
学以致用
3.如何判定一个四边形是正方形?
既是矩形又是菱形的四边形是正方形.
新知探究
有一组邻边相等,并且有一个角是直角的
平行四边形是正方形.
×
×
√
√
下列说法是否正确?为什么?
巩固训练
既是矩形又是菱形的四边形是正方形.
1.四条边都相等的四边形是正方形.
( )
2.对角线互相垂直且相等的四边形是正方形.
( )
3.对角线互相垂直且相等的平行四边形是正方形.
( )
4.对角线相等的菱形是正方形.
( )
试一试,你能行!
已知:如图,△ABC中∠ACB=90°,CD是角平
分线,DE⊥BC,DF⊥AC,垂足分别是E、F.
求证:四边形DECF是正方形.
已知:如图,△ABC中∠ACB=90°,CD是角平分线,DE⊥BC,DF⊥AC,垂足分别是E、F.求证:四边形DECF是正方形.
证明:
∵ DF⊥AC,DE⊥BC,
∴ ∠DEC= ∠DFC=90°,
而∠ACB=90°,
∴四边形DECF是矩形
∵ BD平分∠ABC,
DF⊥BC , DE⊥AB,
∴ DE= DF
∴四边形DEBF是正方形
正方形、菱形、矩形、平行四边形有什么关系?
平行四边形
矩形
菱形
正方形
想一想:
当堂检测、巩固新知
1.正方形具有而菱形不具有的性质是( ).
A.四条边都相等
B.对角线相等
C.对角线平分一组对角
D.对角线垂直且互相平分
当
堂
检
测
B
2.如图,正方形ABCD 的对角线AC,BD 相交于
点O ,且AB=2cm,则OA的长是( ).
C
当堂检测、巩固新知
当堂检测、巩固新知
3.如图,在正方形ABCD 的外侧,作等边三角形
ADE,连接BE,则∠AEB 的度数为( ).
A.10° B.15° C.20° D.12.5°
B
A.AB∥CD,AB=CD,AB=BC,∠ABC=90°
B.∠BAD=∠ABC=∠BCD=∠ADC,AD=AB
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
4.如图,四边形ABCD中,对角线AC,BD相交于点O ,下列条件中不能判定这个四边形是正方形的是( ).
..
当堂检测、巩固新知
D
5.已知四边形ABCD 中,∠A =∠B =∠C =90°,对角线AC,BD相交于点O,请添加一个适当的条件 (填一个即可),使四边形ABCD为正方形.
当堂检测、巩固新知
AB=BC
畅所欲言、盘点收获
知识
方法
课本62页第13题、第15题.
必做题:
见学案选做题.
选做题:
布置作业、拓展提升
老师寄语
统计学家陈希孺:“不论怎么说,机遇无所不在,机遇伴随着人的一生,这是一个无法回避的现实.”
把握好人生的每一次机遇,做一只搏击长空的雄鹰,飞向美好的明天.
T
谢谢
HANK YOU!
义务教育教科书 数学 八年级 下册
理解正方形的概念以及正方形、菱形、矩形、平行四边形之间的关系.
掌握正方形的性质与判定,并能运
用它们进行证明和计算.
1
学习目标
2
矩形的定义.
菱形的定义.
复习回顾
1.类比矩形和菱形的定义,说说正方形的定义.
新知探究
定义:有一组邻边相等,并且有一个角是直角的
平行四边形叫做正方形.
1.类比矩形和菱形的定义,说说正方形的定义.
正方形是矩形吗?
正方形是菱形吗?
正方形既是矩形又是菱形.
新知新究
{BDBED569-4797-4DF1-A0F4-6AAB3CD982D8}
边
角
对角线
对称性
文字
语言
符号
语言
对边平行,
四条边都相等
四个角都是直角
对角线相等且互相
垂直平分,每条对
角线平分一组对角
是轴对称图形,有四条对称轴
∵四边形ABCD
是正方形,
∴AB∥CD,
AD∥BC,
AB =BC =CD =DA.
∵四边形ABCD
是正方形,
∴∠DAB =∠ABC
=∠BCD =∠ADC
=90°.
∵四边形ABCD
是正方形,
∴AC =BD,AC⊥BD,
OA =OC =OB =OD,
∠DAC =∠BAC,
∠DCA =∠BCA,
∠ADB =∠CDB,
∠ABD =∠CBD.
正方形的性质
2.正方形有哪些性质?
新知探究
证明:∵四边形ABCD 是正方形,
∴AC⊥BD,AO=BO=CO=DO.
∴△ABO,△BCO,△CDO,△DAO 都是
等腰直角三角形,并且
△ABO ≌△BCO ≌△CDO ≌△DAO .
已知:如图,四边形ABCD 是正方形,对角线AC,BD 相交于点O.
求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三角形.
正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
图中共有多少个
等腰直角三角形?
学以致用
3.如何判定一个四边形是正方形?
既是矩形又是菱形的四边形是正方形.
新知探究
有一组邻边相等,并且有一个角是直角的
平行四边形是正方形.
×
×
√
√
下列说法是否正确?为什么?
巩固训练
既是矩形又是菱形的四边形是正方形.
1.四条边都相等的四边形是正方形.
( )
2.对角线互相垂直且相等的四边形是正方形.
( )
3.对角线互相垂直且相等的平行四边形是正方形.
( )
4.对角线相等的菱形是正方形.
( )
试一试,你能行!
已知:如图,△ABC中∠ACB=90°,CD是角平
分线,DE⊥BC,DF⊥AC,垂足分别是E、F.
求证:四边形DECF是正方形.
已知:如图,△ABC中∠ACB=90°,CD是角平分线,DE⊥BC,DF⊥AC,垂足分别是E、F.求证:四边形DECF是正方形.
证明:
∵ DF⊥AC,DE⊥BC,
∴ ∠DEC= ∠DFC=90°,
而∠ACB=90°,
∴四边形DECF是矩形
∵ BD平分∠ABC,
DF⊥BC , DE⊥AB,
∴ DE= DF
∴四边形DEBF是正方形
正方形、菱形、矩形、平行四边形有什么关系?
平行四边形
矩形
菱形
正方形
想一想:
当堂检测、巩固新知
1.正方形具有而菱形不具有的性质是( ).
A.四条边都相等
B.对角线相等
C.对角线平分一组对角
D.对角线垂直且互相平分
当
堂
检
测
B
2.如图,正方形ABCD 的对角线AC,BD 相交于
点O ,且AB=2cm,则OA的长是( ).
C
当堂检测、巩固新知
当堂检测、巩固新知
3.如图,在正方形ABCD 的外侧,作等边三角形
ADE,连接BE,则∠AEB 的度数为( ).
A.10° B.15° C.20° D.12.5°
B
A.AB∥CD,AB=CD,AB=BC,∠ABC=90°
B.∠BAD=∠ABC=∠BCD=∠ADC,AD=AB
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
4.如图,四边形ABCD中,对角线AC,BD相交于点O ,下列条件中不能判定这个四边形是正方形的是( ).
..
当堂检测、巩固新知
D
5.已知四边形ABCD 中,∠A =∠B =∠C =90°,对角线AC,BD相交于点O,请添加一个适当的条件 (填一个即可),使四边形ABCD为正方形.
当堂检测、巩固新知
AB=BC
畅所欲言、盘点收获
知识
方法
课本62页第13题、第15题.
必做题:
见学案选做题.
选做题:
布置作业、拓展提升
老师寄语
统计学家陈希孺:“不论怎么说,机遇无所不在,机遇伴随着人的一生,这是一个无法回避的现实.”
把握好人生的每一次机遇,做一只搏击长空的雄鹰,飞向美好的明天.
T
谢谢
HANK YOU!
