华东师大版八年级下册数学:19.3正方形的判定课件 (共15张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学:19.3正方形的判定课件 (共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 726.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 00:00:00 | ||
图片预览





文档简介
正方形的判定
华东师大版八年级(下册)
第19章 矩形、菱形与正方形
19.3 正方形(第2课时)
要使一个图形是正方形,需满足三个条件:①有一个角是直角,②有一组邻边相等 ,③平行四边形.
你还记得吗?
1.什么样的图形是正方形?
2正方形具有什么性质?
边:对边平行,四条边都相等.
角:四个角都等于90°.
对角线:相等、垂直且互相平分.
思边:对边平行,四条边都相等.
角:四个角都等于90°.
对角线:相等、垂直且互相平分.
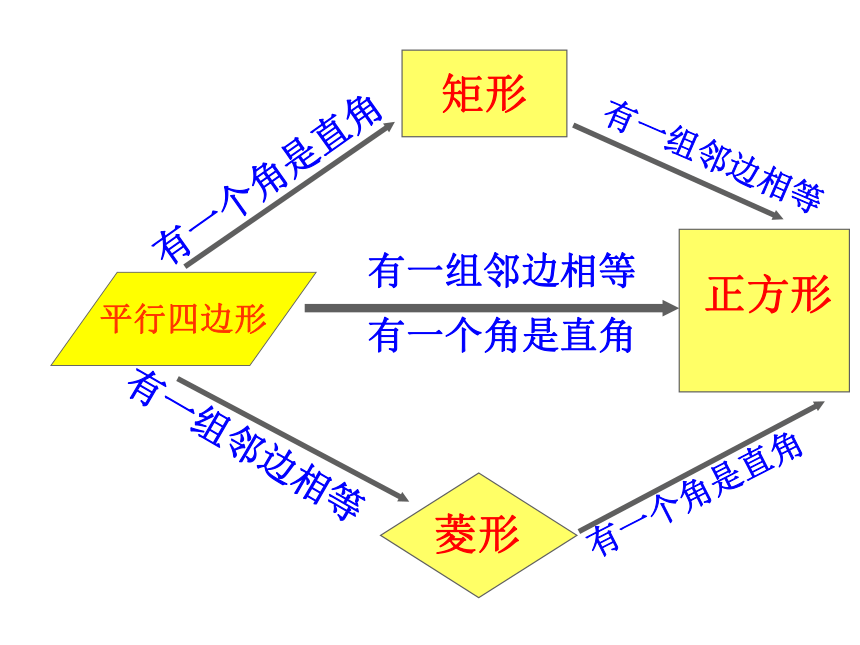
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
通过以上回忆,你觉得什么样的四边形是正方形呢?
讨论
1、要使一个菱形成为正方形需要增加的条件是( )。
2、要使一个矩形成为正方形需添加的条件是( )。
3、要使一个平行四边形成为正方形需要增加的条件是:( )。
有一个角是直角或对角线相等
有一组邻边相等或对角线垂直
有一组邻边相等且有一个角是直角或对角线互相垂直且相等
----下列说法对吗?
1.四个角都相等的四边形是正方形.
2.四条边都相等的四边形是正方形.
3.对角线相等的菱形是正方形.
4.对角线垂直的平行四边形是正方形.
5.对角线互相垂直平分且相等的四边形是正方形.
6.四条边相等且有一个角是直角的四边形是正方形.
7.对角线互相垂直的矩形是正方形.
8.对角线垂直且相等的四边形是正方形.
9.四边相等,有一角是直角的四边形是正方形.
辨一辨
╳
√
╳
╳
√
√
√
╳
√
A
B
C
D
C/
A/
B/
D/
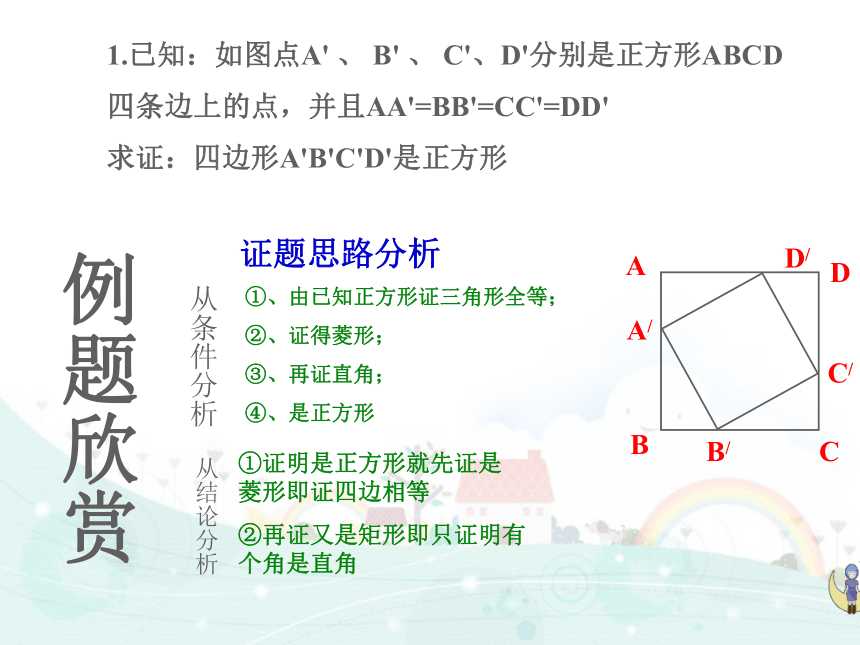
1.已知:如图点A' 、 B' 、 C'、D'分别是正方形ABCD
四条边上的点,并且AA'=BB'=CC'=DD'
求证:四边形A'B'C'D'是正方形
①、由已知正方形证三角形全等;
②、证得菱形;
③、再证直角;
④、是正方形
证题思路分析
例题欣赏
从条件分析
①证明是正方形就先证是 菱形即证四边相等
②再证又是矩形即只证明有个角是直角
从结论分析
证明:∵四边形ABCD是正方形
又∵A`A=B`B=C`C=D`D
∵∠A=∠B=∠C=∠D=90°
∴四边形A`B`C`D`是菱形
又∵∠AD`A`=∠BA`B`, ∠ AA`D`+∠AD`A`=90°
∵∠D`A`B`=180°—(∠AA`D`+∠BA`B`)=90°
∴AB=BC=CD=DA
∴D`A=A`B=B`C=C`D
∴△AA`D`≌△BB`A`≌△CC`B`≌△DD`C`
A`D`=A`B`=B`C`=C`D`
∴ ∠AA`D`+∠BA`B`=90 °
∴四边形A`B`C`D`是正方形
过程欣赏
例2. 如图,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E、F.
求证: 四边形CFDE是正方形.
证明 ∵ DE⊥BC, DF⊥AC, ∠ACB=90°,
∴ ∠DEC=∠ECF=∠CFD=90°,
∴ 四边形CFDE是矩形(有三个角是直角的四边形是矩形),
∵ CD平分∠ACB, DE⊥BC, DF⊥AC,
∴ DE=DF(角平分线上的点到角的两边距离相等).
∴ 四边形CFDE是正方形(有一组邻边相等的矩形是正方形).
练一练
求证:对角线垂直平分且相等的四边形是正方形。
已知:如图,四边形ABCD中对角线AC、BD相交于点O,且AC=BD,AO=CO, BO=DO,AC⊥BD。
求证:四边形ABCD是正方形。
证明: ∵AO=CO,BO=DO
∴四边形ABCD是平行四边形又AC=BD
∴平行四边形ABCD是矩形
又∵AC⊥BD
∴平行四边形ABCD是菱形,
即四边形ABCD是正方形
解题小结:正方形即是特殊的矩形,又是特殊的菱形。它没有明确的判定定理,要判定一个四边形是正方形,基本思路就是证明这个四边形既是菱形又是矩形,从而得到这个四边形是正方形。
请大家先根据题意,画出图形然后写出已知、求证.
5种识
别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
1.矩形ABCD中,四个内角的平分线组成四边形EMFN.判断四边形EMFN的形状,并说明原因.
A
B
C
D
N
F
M
E
提升训练
2.(10分)如图,在△ABC中,∠ACB=90°,BC的
垂直平分线EF交BC于点D,交AB于点E,且CF=BE,
那么当∠A的大小满足什么条件时,四边形BECF是正方形?
请回答并证明你的结论 .
解:当∠A=45°时,
四边形BECF是正方形,
理由:∵EF垂直平分BC,
∴BE=EC,BF=CF.∵CF=BE,
∴BE=EC=CF=BF,∴四边形BECF是菱形.
∵∠A=45°,∠ACB=90°,∴∠EBC=45°,
∴∠EBF=2∠EBC=2×45°=90°,
∴菱形BECF是正方形
提升训练
本节课我们学习了什么?
你有什么收获?说出来与大家分享
课堂小结
正方形的判定
1、定义法 2、矩形菱形法 3、对角线法
特殊的平行四边形的判定小结
作业:
分层作业
再见
华东师大版八年级(下册)
第19章 矩形、菱形与正方形
19.3 正方形(第2课时)
要使一个图形是正方形,需满足三个条件:①有一个角是直角,②有一组邻边相等 ,③平行四边形.
你还记得吗?
1.什么样的图形是正方形?
2正方形具有什么性质?
边:对边平行,四条边都相等.
角:四个角都等于90°.
对角线:相等、垂直且互相平分.
思边:对边平行,四条边都相等.
角:四个角都等于90°.
对角线:相等、垂直且互相平分.
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
通过以上回忆,你觉得什么样的四边形是正方形呢?
讨论
1、要使一个菱形成为正方形需要增加的条件是( )。
2、要使一个矩形成为正方形需添加的条件是( )。
3、要使一个平行四边形成为正方形需要增加的条件是:( )。
有一个角是直角或对角线相等
有一组邻边相等或对角线垂直
有一组邻边相等且有一个角是直角或对角线互相垂直且相等
----下列说法对吗?
1.四个角都相等的四边形是正方形.
2.四条边都相等的四边形是正方形.
3.对角线相等的菱形是正方形.
4.对角线垂直的平行四边形是正方形.
5.对角线互相垂直平分且相等的四边形是正方形.
6.四条边相等且有一个角是直角的四边形是正方形.
7.对角线互相垂直的矩形是正方形.
8.对角线垂直且相等的四边形是正方形.
9.四边相等,有一角是直角的四边形是正方形.
辨一辨
╳
√
╳
╳
√
√
√
╳
√
A
B
C
D
C/
A/
B/
D/
1.已知:如图点A' 、 B' 、 C'、D'分别是正方形ABCD
四条边上的点,并且AA'=BB'=CC'=DD'
求证:四边形A'B'C'D'是正方形
①、由已知正方形证三角形全等;
②、证得菱形;
③、再证直角;
④、是正方形
证题思路分析
例题欣赏
从条件分析
①证明是正方形就先证是 菱形即证四边相等
②再证又是矩形即只证明有个角是直角
从结论分析
证明:∵四边形ABCD是正方形
又∵A`A=B`B=C`C=D`D
∵∠A=∠B=∠C=∠D=90°
∴四边形A`B`C`D`是菱形
又∵∠AD`A`=∠BA`B`, ∠ AA`D`+∠AD`A`=90°
∵∠D`A`B`=180°—(∠AA`D`+∠BA`B`)=90°
∴AB=BC=CD=DA
∴D`A=A`B=B`C=C`D
∴△AA`D`≌△BB`A`≌△CC`B`≌△DD`C`
A`D`=A`B`=B`C`=C`D`
∴ ∠AA`D`+∠BA`B`=90 °
∴四边形A`B`C`D`是正方形
过程欣赏
例2. 如图,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E、F.
求证: 四边形CFDE是正方形.
证明 ∵ DE⊥BC, DF⊥AC, ∠ACB=90°,
∴ ∠DEC=∠ECF=∠CFD=90°,
∴ 四边形CFDE是矩形(有三个角是直角的四边形是矩形),
∵ CD平分∠ACB, DE⊥BC, DF⊥AC,
∴ DE=DF(角平分线上的点到角的两边距离相等).
∴ 四边形CFDE是正方形(有一组邻边相等的矩形是正方形).
练一练
求证:对角线垂直平分且相等的四边形是正方形。
已知:如图,四边形ABCD中对角线AC、BD相交于点O,且AC=BD,AO=CO, BO=DO,AC⊥BD。
求证:四边形ABCD是正方形。
证明: ∵AO=CO,BO=DO
∴四边形ABCD是平行四边形又AC=BD
∴平行四边形ABCD是矩形
又∵AC⊥BD
∴平行四边形ABCD是菱形,
即四边形ABCD是正方形
解题小结:正方形即是特殊的矩形,又是特殊的菱形。它没有明确的判定定理,要判定一个四边形是正方形,基本思路就是证明这个四边形既是菱形又是矩形,从而得到这个四边形是正方形。
请大家先根据题意,画出图形然后写出已知、求证.
5种识
别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
1.矩形ABCD中,四个内角的平分线组成四边形EMFN.判断四边形EMFN的形状,并说明原因.
A
B
C
D
N
F
M
E
提升训练
2.(10分)如图,在△ABC中,∠ACB=90°,BC的
垂直平分线EF交BC于点D,交AB于点E,且CF=BE,
那么当∠A的大小满足什么条件时,四边形BECF是正方形?
请回答并证明你的结论 .
解:当∠A=45°时,
四边形BECF是正方形,
理由:∵EF垂直平分BC,
∴BE=EC,BF=CF.∵CF=BE,
∴BE=EC=CF=BF,∴四边形BECF是菱形.
∵∠A=45°,∠ACB=90°,∴∠EBC=45°,
∴∠EBF=2∠EBC=2×45°=90°,
∴菱形BECF是正方形
提升训练
本节课我们学习了什么?
你有什么收获?说出来与大家分享
课堂小结
正方形的判定
1、定义法 2、矩形菱形法 3、对角线法
特殊的平行四边形的判定小结
作业:
分层作业
再见
