华东师大版八年级下册数学17.3一次函数的复习课件(共22张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学17.3一次函数的复习课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 17:18:18 | ||
图片预览






文档简介
一次函数的复习
一次函数的解析式(表达式)是怎样的?
回忆
Y=kx +b
(其中K、b为常数, K ≠0)
概括:象这样用自变量的一次整式来表示的函数我们称它们为一次函数。
特别地,当b=0时一次函数Y=KX(常数K ≠0 )也叫正比例函数。
一、待定系数法求一次函数的表达式
例:已知:一次函数经过了点A(1,0)和点B(0,-2).求此一次函数的表达式
二、一次函数的图象与性质
1、形状:
一条直线,所以我们又常常说直线Y=KX+b
两点法画图:
(0,b) ( ,0)
2、增减性:
当K>0时,Y随X的增大而增大,此时函数图象从左到右上升;
当K<0时,Y随X的增大而减小,此时函数的图象从左至右下降。
3、解析式Y=kx+b中的k和b的几何意义
(1) b是直线与Y轴交点的纵坐标,即b>0时直线与Y轴的交点在上方, b<0时直线与Y轴的交点在下方。
(3) K的绝对值越大,直线陡度就越大。当K的绝对值等于1时,直线与X轴的夹角是45。
(2)如果K值相等,直线就互相平行。
4、解析式Y=kx+b中的k和b的正负号如何确定函数图象经过哪些象限。
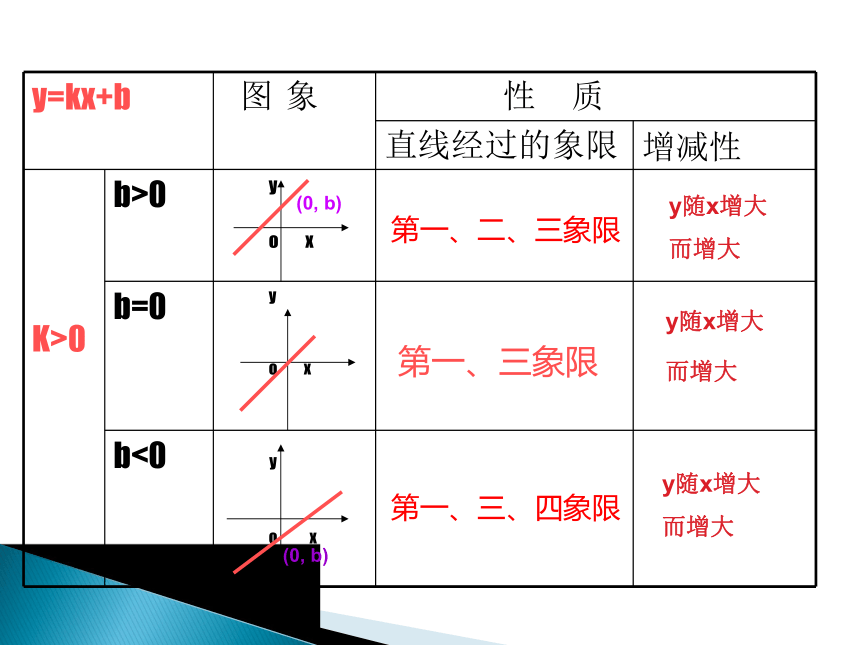
y=kx+b
图 象
性 质
直线经过的象限
增减性
K>0
b>0
y
o x
b=0
y
o x
b<0
y
o x
第一、三象限
y随x增大
而增大
第一、二、三象限
y随x增大
而增大
第一、三、四象限
y随x增大
而增大
(0, b)
(0, b)
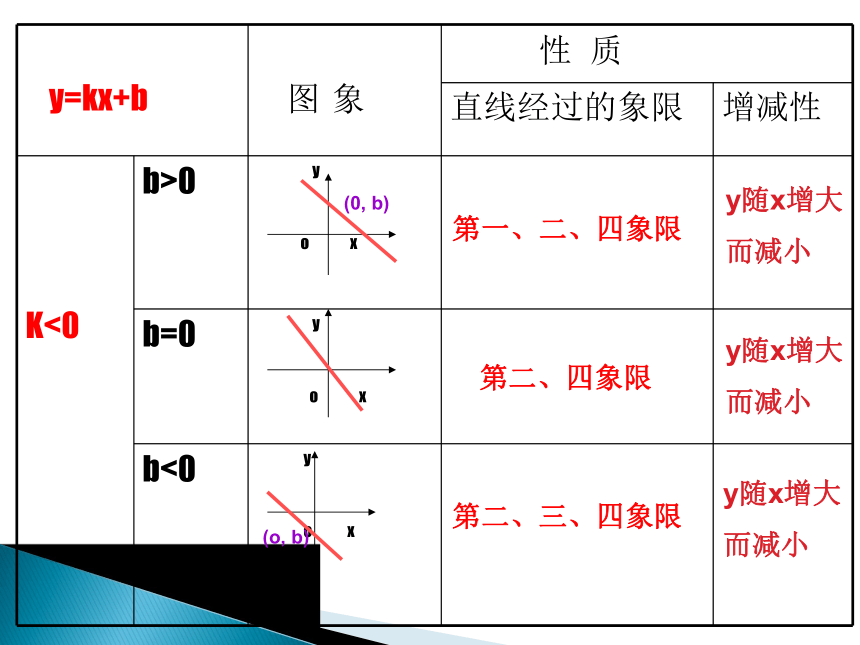
y=kx+b
图 象
性 质
直线经过的象限
增减性
K<0
b>0
y
o x
b=0
y
o x
b<0
y
o x
第二、四象限
y随x增大
而减小
第一、二、四象限
y随x增大
而减小
第二、三、四象限
y随x增大
而减小
(0, b)
(o, b)
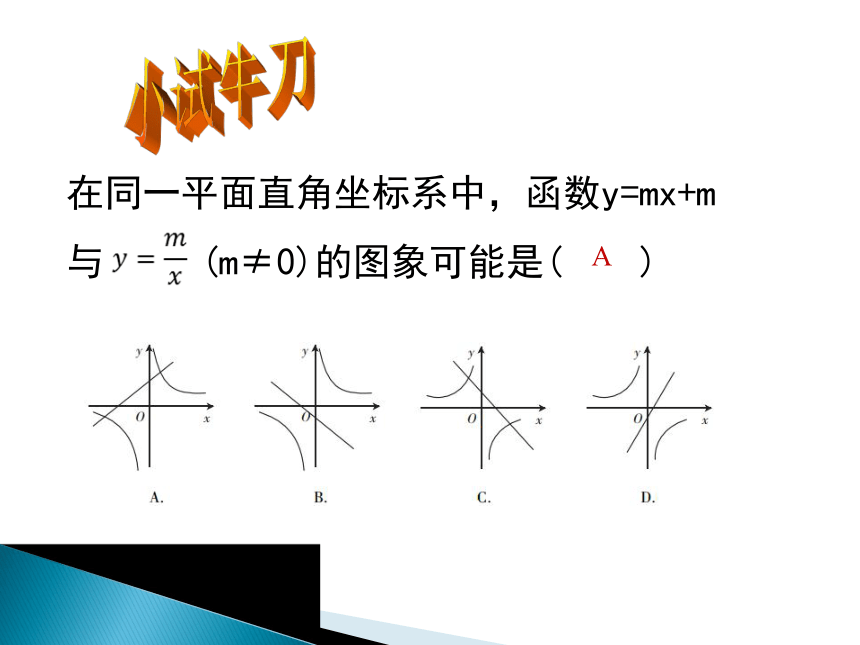
在同一平面直角坐标系中,函数y=mx+m
与 (m≠0)的图象可能是( )
A
1、一次函数y=kx+b的图象如图所示,则方程
kx+b=0的解为( )
A.x=2 B.y=2
C.x=-1 D.y=-1
C
(1) b=4
1、如图,直线y=kx+b交坐标轴于A(-2,0)
B(0,3)两点,则不等式kx+b>0的解集是( )
A.x>3 B.-2<x<3
C.x<-2 D.x>-2
D
2.如图,一次函数y=kx+b(k≠0)的图象与反比例函数 的图象相交于点A(-2,1)和点B .当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
由图象可知,当-2<x<0或x> 时,一次函数的函数值小于反比例函数的函数值.
2、如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m≥nx+4n≥0的整数解为___________________
-2,-3,-4
1、一次函数是满足条件的所有的点组成的一条直线。
2、一元一次方程的解是一次函数图象上的一些特殊的点。
3、二元一次方程组的解是两个一次函数图象的交点。
4、一元一次不等式的解是一次函数图象上的一部份(射线、线段)
五,一次函数的实际应用:
1,右图是某汽车行驶的路程S(km)与时间t(分)的函数关系图,观察图中所提供的信息,解答下列问题:
⑴汽车在前9分钟内的平均速度是 km/分;
⑵汽车在中途停了多长时间? ;
⑶当16≤t≤30时,S与t的函数关系式.
0
S(km)
t(分)
9
30
40
12
16
9 16 30
7分钟
2,小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为 ,小明爸爸与家之间的距离为 ,图中折线OABD、线段EF分别表示 与t之间的函数关系的
(1)求 与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
s(m)
A
O
D
C
B
t(min)
2400
10
12
F
E
s(m)
A
O
D
C
B
t(min)
2400
10
12
F
分析:小明的整个过程是分段函数,有三个函数表达式,这里小明与他爸爸有两次相遇,现要求的是他爸爸与他在归途时相遇,因此应该是EF与BD的交点C.
E
例1、求直线y=2x+3、y=-2x-1及y轴围成的
三角形的面积
若将y轴改为x轴呢?
x
y
O
y=2x+1
y=-2x-1
A
B
C
D
P
六,一次函数中的面积问题
例2、已知直线y=ax+ 分别与x轴和y轴交于
B、C两点,直线y=- x+b与x轴交于点A,并且两直线交点P为(2,2)
(1)求两直线解析式;
(2)求四边形AOCP的面积.
x
y
O
A
B
P(2,2)
C
答案:(2)四边形AOCP的面积是:17/3
3、如图所示,直线l1:y=x+1和l2:y=-2x+m(m>0)交于点P,并且l1交x轴于点A,交y轴于点Q,l2交x轴于点B,若四边形PQOB的面积是
,求直线l2的解析式.
答案:
直线l2的解析式为y=-2x+2.
谈谈你的复习收获
一次函数的解析式(表达式)是怎样的?
回忆
Y=kx +b
(其中K、b为常数, K ≠0)
概括:象这样用自变量的一次整式来表示的函数我们称它们为一次函数。
特别地,当b=0时一次函数Y=KX(常数K ≠0 )也叫正比例函数。
一、待定系数法求一次函数的表达式
例:已知:一次函数经过了点A(1,0)和点B(0,-2).求此一次函数的表达式
二、一次函数的图象与性质
1、形状:
一条直线,所以我们又常常说直线Y=KX+b
两点法画图:
(0,b) ( ,0)
2、增减性:
当K>0时,Y随X的增大而增大,此时函数图象从左到右上升;
当K<0时,Y随X的增大而减小,此时函数的图象从左至右下降。
3、解析式Y=kx+b中的k和b的几何意义
(1) b是直线与Y轴交点的纵坐标,即b>0时直线与Y轴的交点在上方, b<0时直线与Y轴的交点在下方。
(3) K的绝对值越大,直线陡度就越大。当K的绝对值等于1时,直线与X轴的夹角是45。
(2)如果K值相等,直线就互相平行。
4、解析式Y=kx+b中的k和b的正负号如何确定函数图象经过哪些象限。
y=kx+b
图 象
性 质
直线经过的象限
增减性
K>0
b>0
y
o x
b=0
y
o x
b<0
y
o x
第一、三象限
y随x增大
而增大
第一、二、三象限
y随x增大
而增大
第一、三、四象限
y随x增大
而增大
(0, b)
(0, b)
y=kx+b
图 象
性 质
直线经过的象限
增减性
K<0
b>0
y
o x
b=0
y
o x
b<0
y
o x
第二、四象限
y随x增大
而减小
第一、二、四象限
y随x增大
而减小
第二、三、四象限
y随x增大
而减小
(0, b)
(o, b)
在同一平面直角坐标系中,函数y=mx+m
与 (m≠0)的图象可能是( )
A
1、一次函数y=kx+b的图象如图所示,则方程
kx+b=0的解为( )
A.x=2 B.y=2
C.x=-1 D.y=-1
C
(1) b=4
1、如图,直线y=kx+b交坐标轴于A(-2,0)
B(0,3)两点,则不等式kx+b>0的解集是( )
A.x>3 B.-2<x<3
C.x<-2 D.x>-2
D
2.如图,一次函数y=kx+b(k≠0)的图象与反比例函数 的图象相交于点A(-2,1)和点B .当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
由图象可知,当-2<x<0或x> 时,一次函数的函数值小于反比例函数的函数值.
2、如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m≥nx+4n≥0的整数解为___________________
-2,-3,-4
1、一次函数是满足条件的所有的点组成的一条直线。
2、一元一次方程的解是一次函数图象上的一些特殊的点。
3、二元一次方程组的解是两个一次函数图象的交点。
4、一元一次不等式的解是一次函数图象上的一部份(射线、线段)
五,一次函数的实际应用:
1,右图是某汽车行驶的路程S(km)与时间t(分)的函数关系图,观察图中所提供的信息,解答下列问题:
⑴汽车在前9分钟内的平均速度是 km/分;
⑵汽车在中途停了多长时间? ;
⑶当16≤t≤30时,S与t的函数关系式.
0
S(km)
t(分)
9
30
40
12
16
9 16 30
7分钟
2,小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为 ,小明爸爸与家之间的距离为 ,图中折线OABD、线段EF分别表示 与t之间的函数关系的
(1)求 与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
s(m)
A
O
D
C
B
t(min)
2400
10
12
F
E
s(m)
A
O
D
C
B
t(min)
2400
10
12
F
分析:小明的整个过程是分段函数,有三个函数表达式,这里小明与他爸爸有两次相遇,现要求的是他爸爸与他在归途时相遇,因此应该是EF与BD的交点C.
E
例1、求直线y=2x+3、y=-2x-1及y轴围成的
三角形的面积
若将y轴改为x轴呢?
x
y
O
y=2x+1
y=-2x-1
A
B
C
D
P
六,一次函数中的面积问题
例2、已知直线y=ax+ 分别与x轴和y轴交于
B、C两点,直线y=- x+b与x轴交于点A,并且两直线交点P为(2,2)
(1)求两直线解析式;
(2)求四边形AOCP的面积.
x
y
O
A
B
P(2,2)
C
答案:(2)四边形AOCP的面积是:17/3
3、如图所示,直线l1:y=x+1和l2:y=-2x+m(m>0)交于点P,并且l1交x轴于点A,交y轴于点Q,l2交x轴于点B,若四边形PQOB的面积是
,求直线l2的解析式.
答案:
直线l2的解析式为y=-2x+2.
谈谈你的复习收获
