华东师大版八年级下册数学18.2.1平行四边形的判定课件(共28张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学18.2.1平行四边形的判定课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 839.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 17:21:22 | ||
图片预览




文档简介
18.2.1平行四边形的判定
2.平行四边形具有哪些性质?
温故互查
B
C
A
D
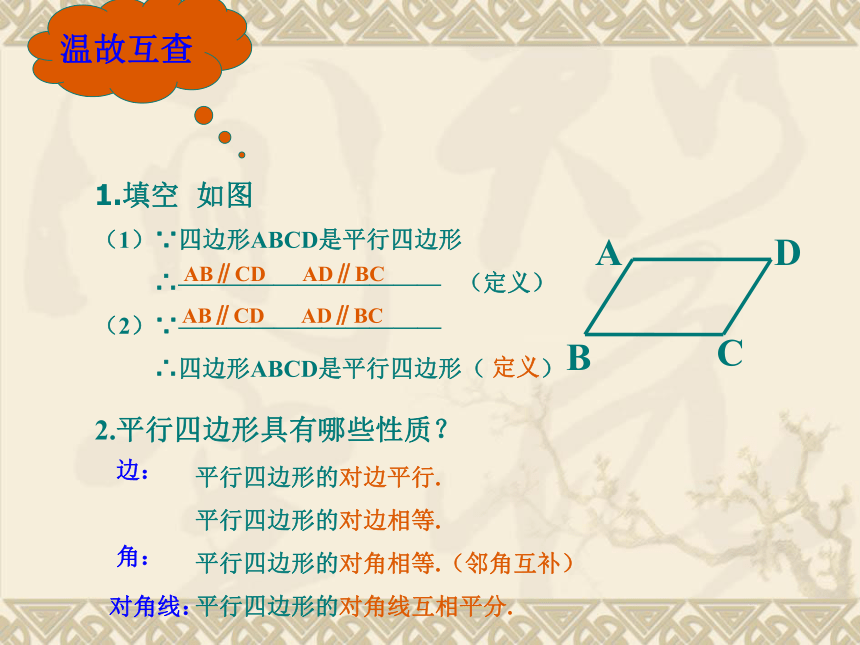
1.填空 如图
(1)∵四边形ABCD是平行四边形
∴——————————— (定义)
(2)∵———————————
∴四边形ABCD是平行四边形( )
AB∥CD AD∥BC
AB∥CD AD∥BC
定义
平行四边形的对边平行.
平行四边形的对边相等.
平行四边形的对角相等.(邻角互补)
平行四边形的对角线互相平分.
边:
角:
对角线:
思考:
通过前面的学习,我们知道平行四边形对边相等、对角相等、对角线互相平分。
反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?这些逆命题是不是真命题呢?
逆向思考 提出猜想
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
逆定理
对边相等
对角相等
对角线互相平分
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:判定这些逆定理的真假?
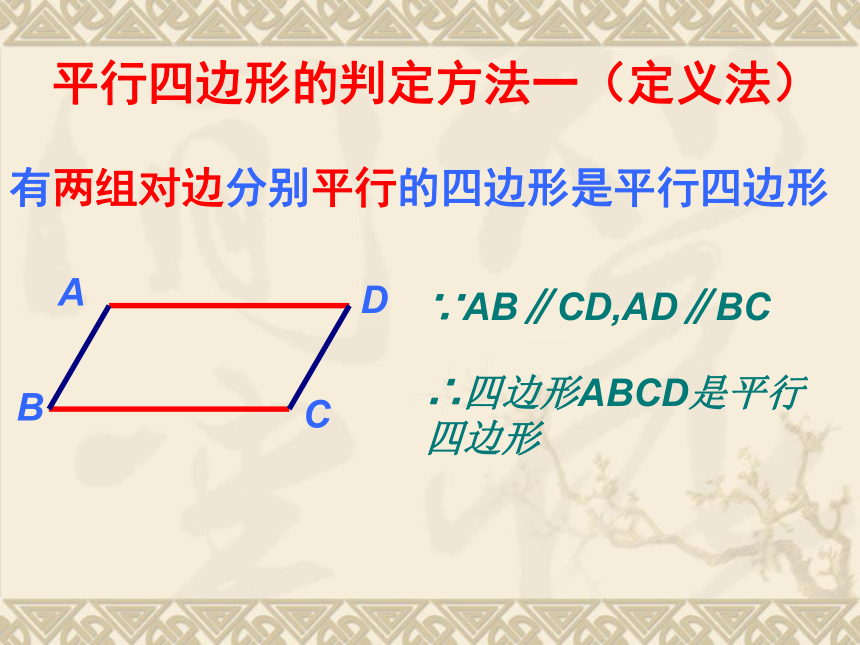
有两组对边分别平行的四边形是平行四边形
平行四边形的判定方法一(定义法)
B
D
A
C
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
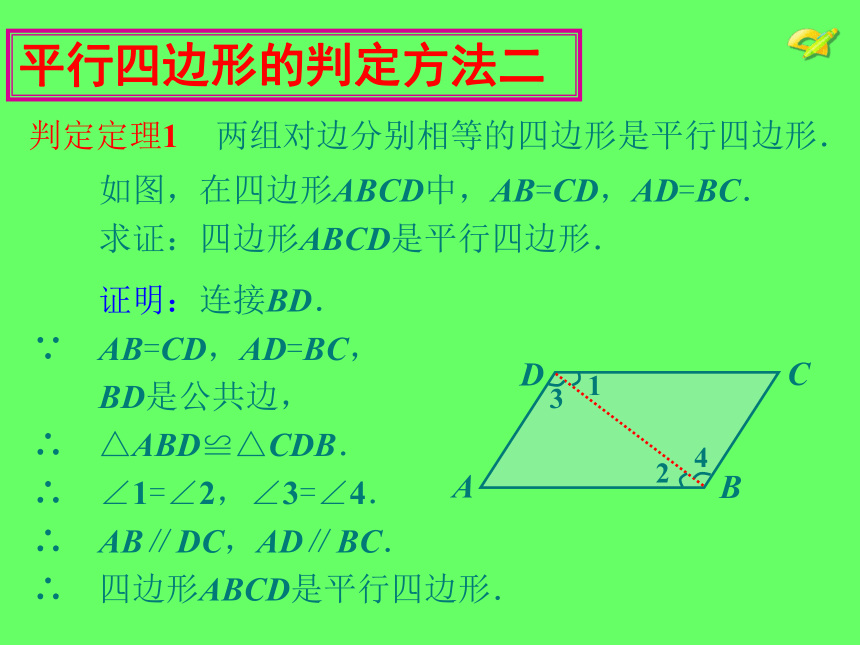
证明:连接BD.
∵ AB=CD,AD=BC,
BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
平行四边形的判定方法二
两组对边分别相等的四边形是平行四边形.
判定定理1
D
A
B
C
1
2
3
4
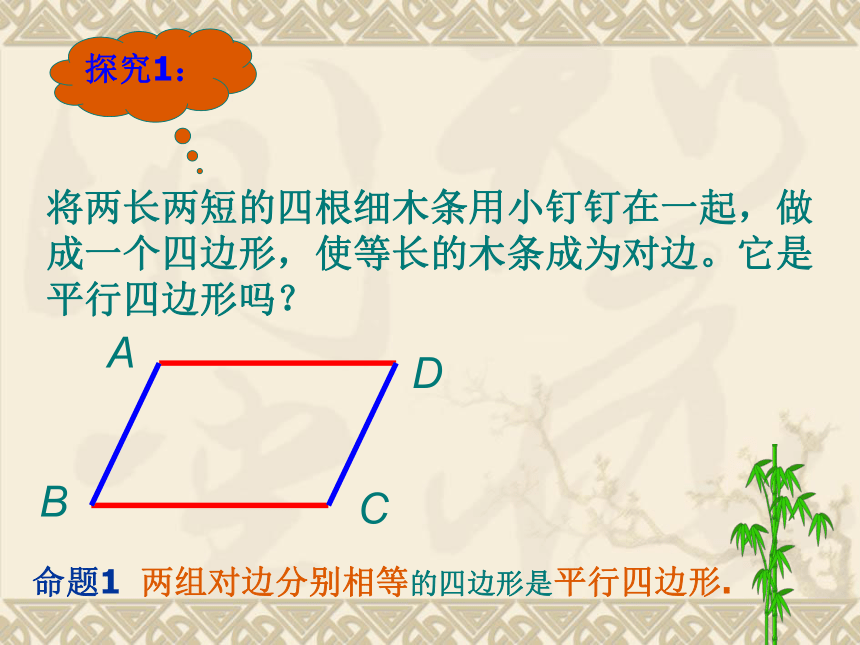
探究1:
将两长两短的四根细木条用小钉钉在一起,做成一个四边形,使等长的木条成为对边。它是平行四边形吗?
A
B
C
D
命题1 两组对边分别相等的四边形是平行四边形.
B
C
A
D
两组对边分别相等的四边形是平行四边形
已知:四边形ABCD
AB=CD,AD=BC
求证:四边形ABCD是平行四边形
证明:连结AC
∵ AB=CD,BC=AD (已知)
又∵ AC=CA (公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2 ∠3=∠4
∴ AB∥CD AD∥BC
∴四边形ABCD是平行四边形(两组对边互相平行的四边形是平行四边形)
2
1
3
4
命题证明
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
平行四边形判定
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。
几何语言:
驶向胜利的彼岸
判定定理1
两组对边分别相等的四边形是平行四边形.
B
C
A
D
符号语言:
∵AB=CD AD=BC
∴ 四边形ABCD是平行四边形
判断下列四边形是否是平行四边形?并说明理由.
B
A
D
C
110°
110°
⑴
4.8㎝
B
A
D
C
4.8㎝
7.6㎝
7.6㎝
⑵
两组对边分别相等的四边形是平行四边形
判定1
两组对边分别平行的四边形是平行四边形
定义
70°
1.在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC= ___ cm, CD= ____cm时,四边形ABCD为平行四边形;
(2)
2、在下列条件中,不能判定四边形是平行四边形的是( )
(A) AB∥CD,AD∥BC
(B) AB=CD,AD=BC
(C) AB∥CD,AD=BC
B
D
A
C
A
B
D
C
(两组对边分别平行)
(两组对边分别相等)
C
小明的爸爸在钉制一个框架时采用了下面的方法:
将两根同样长的木条AB,CD平行放置,再用两根木条AD,BC加固,得到的这个四边形ABCD是什么样的图形?
创设情境:
A
B
C
D
四边形ABCD是平行四边形
猜测:一组对边平行且相等的四边形是平行四边形
A
B
C
D
想一想:一组对边平行且相等的四边形是平行四边形吗?
A
C
D
已知:在四边形ABCD中, AB=CD , AD=BC
求证:四边形ABCD 是平行四边形
证明思路
1
2
3
4
AB∥CD, AD ∥BC
∠1=∠2,∠3=∠4
⊿ABC≌⊿CDA
B
平行四边形的判定方法三
一组对边平行且相等的四边形是平行四边形吗?
A
B
C
D
已知:四边形ABCD中 AB∥CD, AB=CD
求证:四边形ABCD是平行四边形
证明:连接BD
∵ AB∥CD
∴∠ABD = ∠CDB
又∵AB =CD ,BD = DB
∴△ABD ≌△CDB (SAS)
∴AD = CB
∴四边形ABCD是平行四边形
你还有其他证明方法吗
又∵AB =CD
一组对边平行且相等的四边形是平行四边形
平行四边形的判定方法三
B
D
A
C
∵AD = BC
∴四边形ABCD是平行四边形
∥
ABCD
符号语言:
C
A
D
B
B
如图,在四边形ABCD中,
∵ AB = CD
∴四边形ABCD是平行四边形
∥
平行且相等(记作:“= ”)
∥
判定方法
一组对边平行且相等的四边形是平行四边形
在?ABCD中,已知M和N分别是AB、DC上的中点,试说明四边形
BMDN也是平行四边形。
B
C
D
M
N
A
解:∵四边形ABCD是平行四边形
∴AB∥CD 且 AB=CD
∵ M和N分别是AB、DC上的中点
∴ BM∥DN 且 BM=DN
∴四边形BMDN也是平行四边形
3 如图,AB=DC=EF,AD=BC,DE=CF,图中有哪 些互相平行的线段?
F
A
B
C
D
E
解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF
AD∥BC
AB=DC
AD=BC
四边形ABCD是平行四边形
AB∥DC
DC∥EF
DC=EF
DE=CF
四边形CDEF是平行四边形
DE∥CF
AB∥ DC∥EF
理由如下:
A
B
C
D
E
F
例一,在?ABCD中,已知点F和点E分别在AD和BC上,且AF=CE,连结CF和AE,说明四边形AFCE是平行四边形。
要说明四边形AFCE是平行四边形
有一组对边平行且相等
两组对边都分别相等
两组对边都分别平行
1、在四边形ABCD中如果AB∥DC,可添加条件__________________可使四边形ABCD成为平行四边形
AD∥BC
或 AB=DC
2、判断:在四边形ABCD中如果AB∥DC,AD=BC,那么四边形ABCD是否是一个平行四边形
B
D
A
C
在下面的格点图中,以格点为顶点你能画出多少个平行四边形?
如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?
AB ∥ DC∥ EF
AD ∥ BC
DE ∥ CF
A
B
C
D
E
F
在上题中,将“E,F分别是AB,CD的中点”改为
“E,F分别是AB,CD上的点,且AE=CF”,结论是否
仍然成立?请说明理由.
基础练习
例1 如图,在 ABCD中,E,F分别是AB,CD的
中点.求证:四边形EBFD是平行四边形.
基础练习
例2 如图,四边形AEFD和EBCF都是平行四边形.
求证:四边形ABCD是平行四边形.(P50 6题)
A
B
C
D
E
F
驶向胜利的彼岸
通过本节课的学习你收获了什么?
作业布置 课本P91 4、5、10
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
2.平行四边形具有哪些性质?
温故互查
B
C
A
D
1.填空 如图
(1)∵四边形ABCD是平行四边形
∴——————————— (定义)
(2)∵———————————
∴四边形ABCD是平行四边形( )
AB∥CD AD∥BC
AB∥CD AD∥BC
定义
平行四边形的对边平行.
平行四边形的对边相等.
平行四边形的对角相等.(邻角互补)
平行四边形的对角线互相平分.
边:
角:
对角线:
思考:
通过前面的学习,我们知道平行四边形对边相等、对角相等、对角线互相平分。
反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?这些逆命题是不是真命题呢?
逆向思考 提出猜想
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
逆定理
对边相等
对角相等
对角线互相平分
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:判定这些逆定理的真假?
有两组对边分别平行的四边形是平行四边形
平行四边形的判定方法一(定义法)
B
D
A
C
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
证明:连接BD.
∵ AB=CD,AD=BC,
BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
平行四边形的判定方法二
两组对边分别相等的四边形是平行四边形.
判定定理1
D
A
B
C
1
2
3
4
探究1:
将两长两短的四根细木条用小钉钉在一起,做成一个四边形,使等长的木条成为对边。它是平行四边形吗?
A
B
C
D
命题1 两组对边分别相等的四边形是平行四边形.
B
C
A
D
两组对边分别相等的四边形是平行四边形
已知:四边形ABCD
AB=CD,AD=BC
求证:四边形ABCD是平行四边形
证明:连结AC
∵ AB=CD,BC=AD (已知)
又∵ AC=CA (公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2 ∠3=∠4
∴ AB∥CD AD∥BC
∴四边形ABCD是平行四边形(两组对边互相平行的四边形是平行四边形)
2
1
3
4
命题证明
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
平行四边形判定
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。
几何语言:
驶向胜利的彼岸
判定定理1
两组对边分别相等的四边形是平行四边形.
B
C
A
D
符号语言:
∵AB=CD AD=BC
∴ 四边形ABCD是平行四边形
判断下列四边形是否是平行四边形?并说明理由.
B
A
D
C
110°
110°
⑴
4.8㎝
B
A
D
C
4.8㎝
7.6㎝
7.6㎝
⑵
两组对边分别相等的四边形是平行四边形
判定1
两组对边分别平行的四边形是平行四边形
定义
70°
1.在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC= ___ cm, CD= ____cm时,四边形ABCD为平行四边形;
(2)
2、在下列条件中,不能判定四边形是平行四边形的是( )
(A) AB∥CD,AD∥BC
(B) AB=CD,AD=BC
(C) AB∥CD,AD=BC
B
D
A
C
A
B
D
C
(两组对边分别平行)
(两组对边分别相等)
C
小明的爸爸在钉制一个框架时采用了下面的方法:
将两根同样长的木条AB,CD平行放置,再用两根木条AD,BC加固,得到的这个四边形ABCD是什么样的图形?
创设情境:
A
B
C
D
四边形ABCD是平行四边形
猜测:一组对边平行且相等的四边形是平行四边形
A
B
C
D
想一想:一组对边平行且相等的四边形是平行四边形吗?
A
C
D
已知:在四边形ABCD中, AB=CD , AD=BC
求证:四边形ABCD 是平行四边形
证明思路
1
2
3
4
AB∥CD, AD ∥BC
∠1=∠2,∠3=∠4
⊿ABC≌⊿CDA
B
平行四边形的判定方法三
一组对边平行且相等的四边形是平行四边形吗?
A
B
C
D
已知:四边形ABCD中 AB∥CD, AB=CD
求证:四边形ABCD是平行四边形
证明:连接BD
∵ AB∥CD
∴∠ABD = ∠CDB
又∵AB =CD ,BD = DB
∴△ABD ≌△CDB (SAS)
∴AD = CB
∴四边形ABCD是平行四边形
你还有其他证明方法吗
又∵AB =CD
一组对边平行且相等的四边形是平行四边形
平行四边形的判定方法三
B
D
A
C
∵AD = BC
∴四边形ABCD是平行四边形
∥
ABCD
符号语言:
C
A
D
B
B
如图,在四边形ABCD中,
∵ AB = CD
∴四边形ABCD是平行四边形
∥
平行且相等(记作:“= ”)
∥
判定方法
一组对边平行且相等的四边形是平行四边形
在?ABCD中,已知M和N分别是AB、DC上的中点,试说明四边形
BMDN也是平行四边形。
B
C
D
M
N
A
解:∵四边形ABCD是平行四边形
∴AB∥CD 且 AB=CD
∵ M和N分别是AB、DC上的中点
∴ BM∥DN 且 BM=DN
∴四边形BMDN也是平行四边形
3 如图,AB=DC=EF,AD=BC,DE=CF,图中有哪 些互相平行的线段?
F
A
B
C
D
E
解:图中互相平行的线段有:AB//DC//EF, AD//BC, DE//CF
AD∥BC
AB=DC
AD=BC
四边形ABCD是平行四边形
AB∥DC
DC∥EF
DC=EF
DE=CF
四边形CDEF是平行四边形
DE∥CF
AB∥ DC∥EF
理由如下:
A
B
C
D
E
F
例一,在?ABCD中,已知点F和点E分别在AD和BC上,且AF=CE,连结CF和AE,说明四边形AFCE是平行四边形。
要说明四边形AFCE是平行四边形
有一组对边平行且相等
两组对边都分别相等
两组对边都分别平行
1、在四边形ABCD中如果AB∥DC,可添加条件__________________可使四边形ABCD成为平行四边形
AD∥BC
或 AB=DC
2、判断:在四边形ABCD中如果AB∥DC,AD=BC,那么四边形ABCD是否是一个平行四边形
B
D
A
C
在下面的格点图中,以格点为顶点你能画出多少个平行四边形?
如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?
AB ∥ DC∥ EF
AD ∥ BC
DE ∥ CF
A
B
C
D
E
F
在上题中,将“E,F分别是AB,CD的中点”改为
“E,F分别是AB,CD上的点,且AE=CF”,结论是否
仍然成立?请说明理由.
基础练习
例1 如图,在 ABCD中,E,F分别是AB,CD的
中点.求证:四边形EBFD是平行四边形.
基础练习
例2 如图,四边形AEFD和EBCF都是平行四边形.
求证:四边形ABCD是平行四边形.(P50 6题)
A
B
C
D
E
F
驶向胜利的彼岸
通过本节课的学习你收获了什么?
作业布置 课本P91 4、5、10
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
