华东师大版七年级数学下册 9.1.2三角形的内角和与外角和 (共24张PPT)
文档属性
| 名称 | 华东师大版七年级数学下册 9.1.2三角形的内角和与外角和 (共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 901.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 17:20:27 | ||
图片预览








文档简介
9.1.2三角形的内角和
学习目标:
1、探索并证明三角形的内角和定理,掌握它的推论:直角三角形的两个锐角互余。
2、能利用三角形的内角和定理和推论解决相关问题。
重点:三角形的内角和定理和它的推论
难点:三角形内角和定理的证明
复习回顾
1、三角形的中线
三角形的角平分线
各有3条
都在三角形内部
交于一点
2、三角形的高(3条,交于一点)
锐角三角形3条高的交点在三角形的内部
直角三角形3条高的交点是直角顶点
钝角三角形3条高的交点在三角形的外部
3、三角形的一条中线将三角形分成面积相等的两个三角形
知识链接
平行线的性质
{
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
探究新知1:三角形的内角和定理
三角形的内角和等于180°
你能否能用几何推理的方法加以证明?
知识点1:三角形的内角和
已知:∠A、∠B、∠C分别是ΔABC的三个内角,
求证:∠A+∠B+∠C=180°
A
B
C
视频
E
F
1
2
证明:过点A作EF∥BC
∴∠1=∠B
∠2=∠C
(两直线平行,内错角相等)
∵∠BAC+∠1+∠2=180°
∴∠BAC+∠B+∠C=180°
(等量代换)
已知:∠A、∠B、∠C分别是ΔABC的三个内角,
求证:∠A+∠B+∠C=180°
A
B
C
课本
D
E
1
2
证明:延长BC,过点C作CE∥AB
∴∠A=∠1
∠B=∠2
(两直线平行,
内错角相等)
(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
(等量代换)
已知:∠A、∠B、∠C分别是ΔABC的三个内角,
求证:∠A+∠B+∠C=180°
A
B
C
探究
D
E
F
3
4
1
2
证明:过BC边上一点D,作
DE∥AB,DF∥AC
∴∠B=∠1 ∠C=∠2
(两直线平行,同位角相等)
∠A+∠3=180° ∠4+∠3=180°
(两直线平行,同旁内角互补)
∴∠A=∠4(等角的补交相等)
∵∠1+∠4+∠2=180°
∴∠A+∠B+∠C=180°(等量代换)
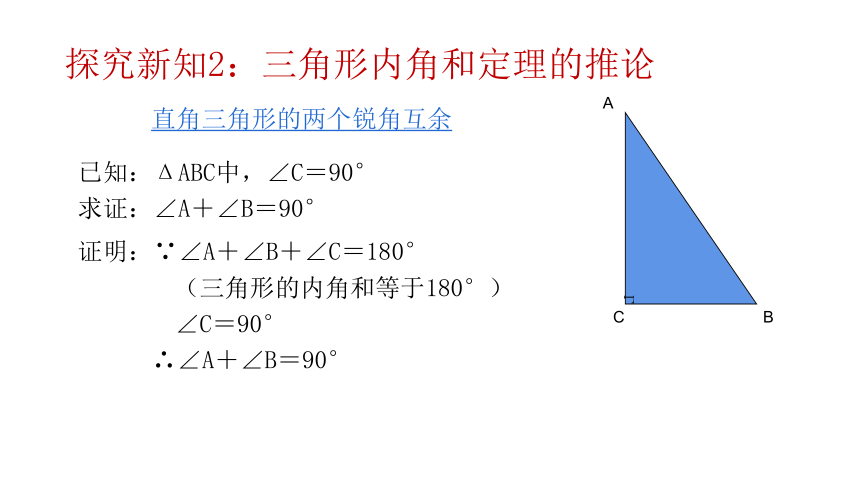
探究新知2:三角形内角和定理的推论
Γ
A
B
C
已知:ΔABC中,∠C=90°
求证:∠A+∠B=90°
证明:∵∠A+∠B+∠C=180°
(三角形的内角和等于180°)
∠C=90°
∴∠A+∠B=90°
直角三角形的两个锐角互余
应 用1
已知:ΔABC中,∠C=20°,∠A-∠B=40°,求∠A和∠B
解:∵∠A+∠B+∠C=180°
(三角形的内角和等于180°)
∠C=20°
∴∠A+∠B=180°-20°=160°
∵∠A-∠B=40°
∴
{
∠A-∠B=40°
∠A+∠B=160°
解得
{
∠A=100°
∠B=40°
即∠A是100°,∠B是40°
应 用2
已知:直角三角形ABC中,∠A:∠B=2:3,求∠A和∠B
Γ
A
B
C
解:∵ΔABC是直角三角形
∴∠A+∠B=90°
(直角三角形的两个锐角互余)
∵∠A:∠B=2:3
∴设∠A=2x,∠B=3x
∴2x+3x=90°解得x=18°
∴∠A=2×18°=36°
∠B=3×18°=54°
小 结
1、三角形的内角和等于180°
2、直角三角形的两个锐角互余
作 业
1、已知,在ΔABC中,∠A=30°,3∠B=2∠C,求∠B、∠C,并判断ΔABC的形状
2、解下列方程
3、一同学解方程 ,去分母时方程右边的-2忘了乘以14,因而求出的解是x=-20,试求 a的值,并求出正确的解。
9.1.2三角形的外角和
学习目标:
1.理解三角形的外角的两条性质以及三角形的内角和与外角和.
2.会利用“三角形的一个外角等于和它不相邻的两个内角的和”进行有关计算.
重点:掌握三角形外角的性质以及其外角的和.
难点:三角形角的有关计算.
复习回顾
1、三角形的内角和定理
2、三角形内角和定理的推论
三角形的内角和等于180?
直角三角形的两个锐角互余
知识点1:三角形外角的两个性质
合作探究:三角形的外角与内角的关系
外角∠CBD与其他两个不相邻的内角有什么关系呢? ∵∠CBD+∠ABC=180°
∠C+∠A+∠ABC=180°(三角形的内角和等于180?) ∴∠CBD=∠C+∠A
1、三角形的一个外角等于与它不相邻的两个内角的和
2、三角形的一个外角大于任何一个与它不相邻的内角
知识点2:三角形的外角和
与三角形的每个内角相邻的外角分别有两个,这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.
你能用“三角形的内角和等于180°”来说明图中∠1+∠2+∠3=360°吗?
证明:∵∠1+∠ACB=180?
∠2+∠BAC=180?
∠3+∠ABC=180°
已知:∠1、∠2、∠3分别是?ABC的三个外角
求证:∠1+∠2+∠3=360?
∴∠1+∠2+∠3+∠ACB+∠ABC+∠BAC
=180°×3=540?
又∵∠ACB+∠BAC+∠ABC=180°
∴∠1+∠2+∠3=540?-180°=360°
结论:三角形的外角和等于360?
应用1
如图,n∥m,∠1=115°,∠2=95°,求∠3的度数.
n
m
1
2
3
B
E
F
P
解:过点F作FB∥n
∵n∥m
∴FB∥m
∴∠1+∠EFB=180?
∠3+∠BFP=180?
(两直线平行,同旁内角互补)
∴∠1+∠3+∠EFB+∠BFP=360°
∵∠1=115°
∠2=∠EFB+∠BFP=95°
∴115°+∠3+95°=360°
∴∠3=150°即∠3是150°
应用1
如图:n∥m,∠1=115°,∠2=95°,求∠3的度数.
n
m
1
2
3
E
F
P
A
4
5
A
4
5
解:延长EF交m与点A
∵n∥m
∴∠1+∠4=180°
∵∠1=115°
∴∠4=65°
∵∠2+∠5=180° ∠2=95°
∴∠5=85°
∵∠3=∠4+∠5(三角形的一个外角等于与它不相邻的两个内角的和)
∴∠3=65°+85°=150°
即∠3的度数是150°
小 结
知识点1、三角形外角的两个性质
1、三角形的一个外角等于与它不相邻的两个内角的和
2、三角形的一个外角大于任何一个与它不相邻的内角
知识点2、三角形的外角
1、定义:从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.
2、三角形的外角和等于360°
1.如图所示x=________
2.如图∠C=∠1,则∠C与∠B
的大小关系是______________
3.三角形三个外角度数的比是3∶4∶5,这个三角形是______三角形 4.三角形的三个外角中钝角的个数最多有______个,至少有______个。 5.如图∠A=31°,∠C=26°,∠B=34°,
则∠EOB=________
课堂检测
作 业
1、解答题:如图1,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°
求:(1)∠B的度数;(2)∠C的度数.
2、如图,在直角△ABC中,∠C=90°,BD平分∠ABC交AC于D,AP平分∠BAC交BD于P,求∠BPA的度数。
学习目标:
1、探索并证明三角形的内角和定理,掌握它的推论:直角三角形的两个锐角互余。
2、能利用三角形的内角和定理和推论解决相关问题。
重点:三角形的内角和定理和它的推论
难点:三角形内角和定理的证明
复习回顾
1、三角形的中线
三角形的角平分线
各有3条
都在三角形内部
交于一点
2、三角形的高(3条,交于一点)
锐角三角形3条高的交点在三角形的内部
直角三角形3条高的交点是直角顶点
钝角三角形3条高的交点在三角形的外部
3、三角形的一条中线将三角形分成面积相等的两个三角形
知识链接
平行线的性质
{
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
探究新知1:三角形的内角和定理
三角形的内角和等于180°
你能否能用几何推理的方法加以证明?
知识点1:三角形的内角和
已知:∠A、∠B、∠C分别是ΔABC的三个内角,
求证:∠A+∠B+∠C=180°
A
B
C
视频
E
F
1
2
证明:过点A作EF∥BC
∴∠1=∠B
∠2=∠C
(两直线平行,内错角相等)
∵∠BAC+∠1+∠2=180°
∴∠BAC+∠B+∠C=180°
(等量代换)
已知:∠A、∠B、∠C分别是ΔABC的三个内角,
求证:∠A+∠B+∠C=180°
A
B
C
课本
D
E
1
2
证明:延长BC,过点C作CE∥AB
∴∠A=∠1
∠B=∠2
(两直线平行,
内错角相等)
(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
(等量代换)
已知:∠A、∠B、∠C分别是ΔABC的三个内角,
求证:∠A+∠B+∠C=180°
A
B
C
探究
D
E
F
3
4
1
2
证明:过BC边上一点D,作
DE∥AB,DF∥AC
∴∠B=∠1 ∠C=∠2
(两直线平行,同位角相等)
∠A+∠3=180° ∠4+∠3=180°
(两直线平行,同旁内角互补)
∴∠A=∠4(等角的补交相等)
∵∠1+∠4+∠2=180°
∴∠A+∠B+∠C=180°(等量代换)
探究新知2:三角形内角和定理的推论
Γ
A
B
C
已知:ΔABC中,∠C=90°
求证:∠A+∠B=90°
证明:∵∠A+∠B+∠C=180°
(三角形的内角和等于180°)
∠C=90°
∴∠A+∠B=90°
直角三角形的两个锐角互余
应 用1
已知:ΔABC中,∠C=20°,∠A-∠B=40°,求∠A和∠B
解:∵∠A+∠B+∠C=180°
(三角形的内角和等于180°)
∠C=20°
∴∠A+∠B=180°-20°=160°
∵∠A-∠B=40°
∴
{
∠A-∠B=40°
∠A+∠B=160°
解得
{
∠A=100°
∠B=40°
即∠A是100°,∠B是40°
应 用2
已知:直角三角形ABC中,∠A:∠B=2:3,求∠A和∠B
Γ
A
B
C
解:∵ΔABC是直角三角形
∴∠A+∠B=90°
(直角三角形的两个锐角互余)
∵∠A:∠B=2:3
∴设∠A=2x,∠B=3x
∴2x+3x=90°解得x=18°
∴∠A=2×18°=36°
∠B=3×18°=54°
小 结
1、三角形的内角和等于180°
2、直角三角形的两个锐角互余
作 业
1、已知,在ΔABC中,∠A=30°,3∠B=2∠C,求∠B、∠C,并判断ΔABC的形状
2、解下列方程
3、一同学解方程 ,去分母时方程右边的-2忘了乘以14,因而求出的解是x=-20,试求 a的值,并求出正确的解。
9.1.2三角形的外角和
学习目标:
1.理解三角形的外角的两条性质以及三角形的内角和与外角和.
2.会利用“三角形的一个外角等于和它不相邻的两个内角的和”进行有关计算.
重点:掌握三角形外角的性质以及其外角的和.
难点:三角形角的有关计算.
复习回顾
1、三角形的内角和定理
2、三角形内角和定理的推论
三角形的内角和等于180?
直角三角形的两个锐角互余
知识点1:三角形外角的两个性质
合作探究:三角形的外角与内角的关系
外角∠CBD与其他两个不相邻的内角有什么关系呢? ∵∠CBD+∠ABC=180°
∠C+∠A+∠ABC=180°(三角形的内角和等于180?) ∴∠CBD=∠C+∠A
1、三角形的一个外角等于与它不相邻的两个内角的和
2、三角形的一个外角大于任何一个与它不相邻的内角
知识点2:三角形的外角和
与三角形的每个内角相邻的外角分别有两个,这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.
你能用“三角形的内角和等于180°”来说明图中∠1+∠2+∠3=360°吗?
证明:∵∠1+∠ACB=180?
∠2+∠BAC=180?
∠3+∠ABC=180°
已知:∠1、∠2、∠3分别是?ABC的三个外角
求证:∠1+∠2+∠3=360?
∴∠1+∠2+∠3+∠ACB+∠ABC+∠BAC
=180°×3=540?
又∵∠ACB+∠BAC+∠ABC=180°
∴∠1+∠2+∠3=540?-180°=360°
结论:三角形的外角和等于360?
应用1
如图,n∥m,∠1=115°,∠2=95°,求∠3的度数.
n
m
1
2
3
B
E
F
P
解:过点F作FB∥n
∵n∥m
∴FB∥m
∴∠1+∠EFB=180?
∠3+∠BFP=180?
(两直线平行,同旁内角互补)
∴∠1+∠3+∠EFB+∠BFP=360°
∵∠1=115°
∠2=∠EFB+∠BFP=95°
∴115°+∠3+95°=360°
∴∠3=150°即∠3是150°
应用1
如图:n∥m,∠1=115°,∠2=95°,求∠3的度数.
n
m
1
2
3
E
F
P
A
4
5
A
4
5
解:延长EF交m与点A
∵n∥m
∴∠1+∠4=180°
∵∠1=115°
∴∠4=65°
∵∠2+∠5=180° ∠2=95°
∴∠5=85°
∵∠3=∠4+∠5(三角形的一个外角等于与它不相邻的两个内角的和)
∴∠3=65°+85°=150°
即∠3的度数是150°
小 结
知识点1、三角形外角的两个性质
1、三角形的一个外角等于与它不相邻的两个内角的和
2、三角形的一个外角大于任何一个与它不相邻的内角
知识点2、三角形的外角
1、定义:从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.
2、三角形的外角和等于360°
1.如图所示x=________
2.如图∠C=∠1,则∠C与∠B
的大小关系是______________
3.三角形三个外角度数的比是3∶4∶5,这个三角形是______三角形 4.三角形的三个外角中钝角的个数最多有______个,至少有______个。 5.如图∠A=31°,∠C=26°,∠B=34°,
则∠EOB=________
课堂检测
作 业
1、解答题:如图1,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°
求:(1)∠B的度数;(2)∠C的度数.
2、如图,在直角△ABC中,∠C=90°,BD平分∠ABC交AC于D,AP平分∠BAC交BD于P,求∠BPA的度数。
