华东师大版七年级下册数学 9.2 多边形的内角和 (共17张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 9.2 多边形的内角和 (共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 707.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 10:54:54 | ||
图片预览



文档简介
义务教育教科书
华东师大版《数学》七年级下册
类比
1、你能说一说什么叫三角形?
2、你能说出什么叫四边形、五边形、多边形吗?
3、你能说出多边形的顶点、边、内角、外角吗?
一、探究新知
问题:
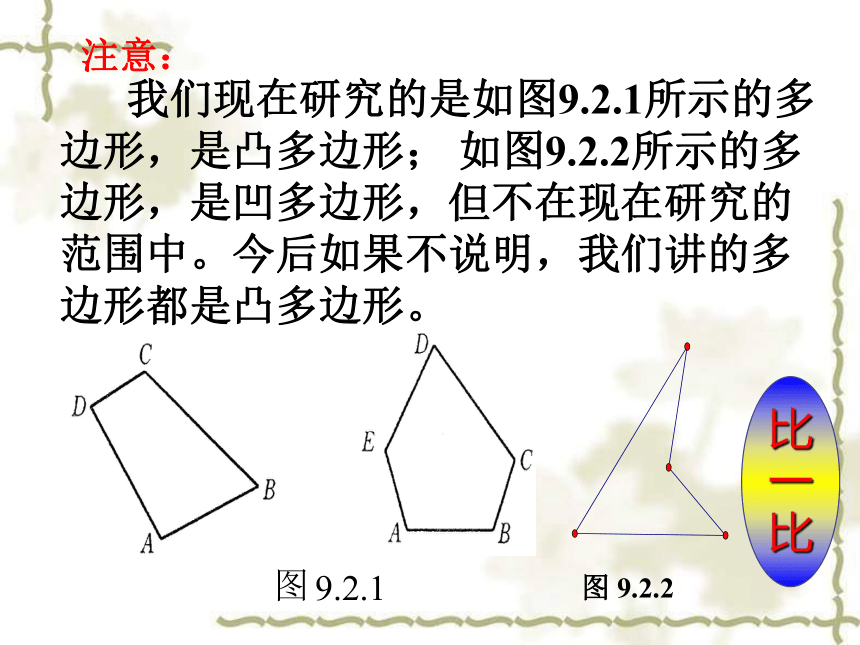
我们现在研究的是如图9.2.1所示的多边形,是凸多边形; 如图9.2.2所示的多边形,是凹多边形,但不在现在研究的范围中。今后如果不说明,我们讲的多边形都是凸多边形。
图 9.2.2
比
一
比
注意:
图
9.2.1
三条边都相等,三个角也都相等
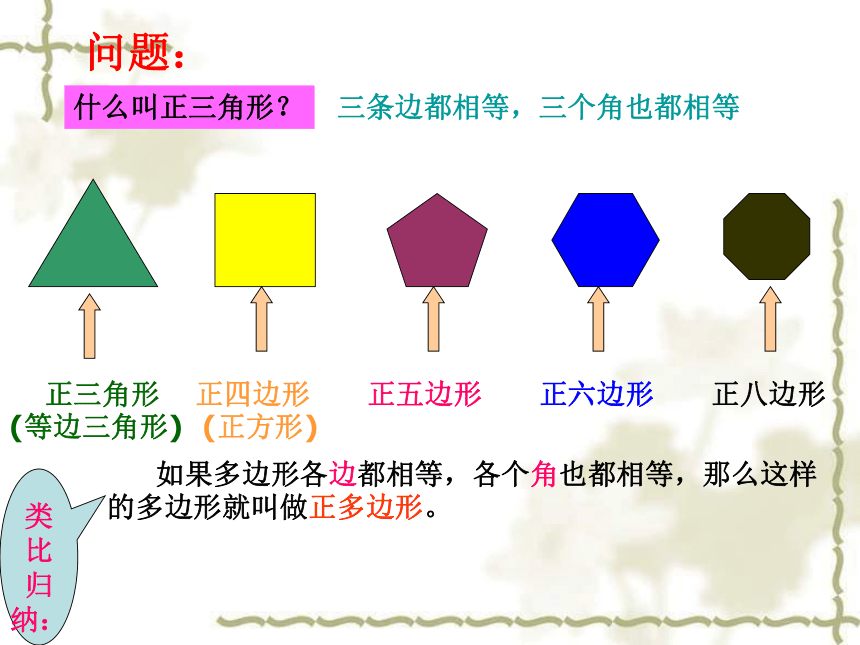
如果多边形各边都相等,各个角也都相等,那么这样的多边形就叫做正多边形。
正三角形
正四边形
正五边形
正六边形
正八边形
(等边三角形)
(正方形)
问题:
类比归纳:
什么叫正三角形?
画出连结下面四点的所有线段:
连结多边形不相邻的两个顶点的线段叫做多边形的对角线。
做
一
做
A
B
C
D
问题:
D
A
B
C
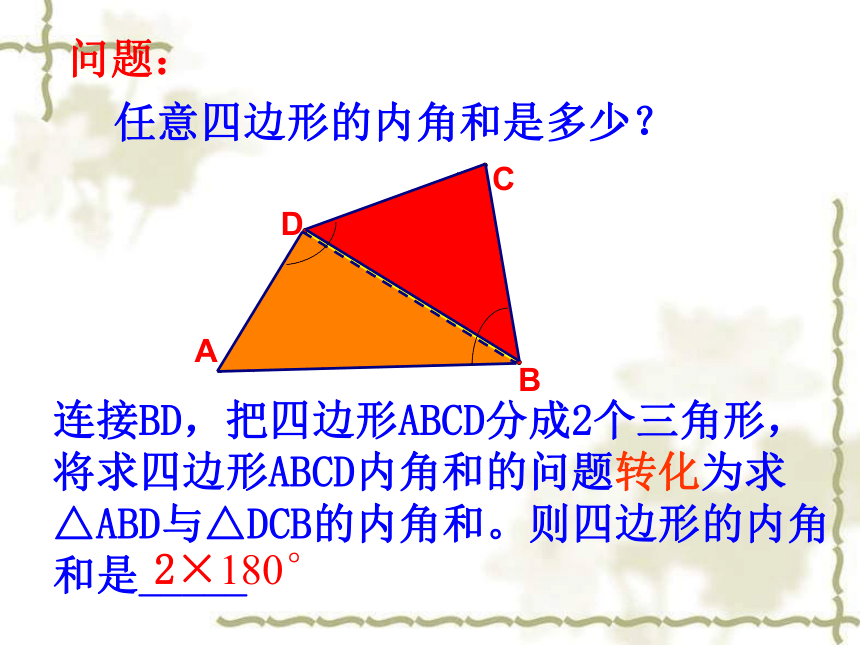
连接BD,把四边形ABCD分成2个三角形,将求四边形ABCD内角和的问题转化为求△ABD与△DCB的内角和。则四边形的内角和是_____
任意四边形的内角和是多少?
2×180°
问题:
E
A
B
C
D
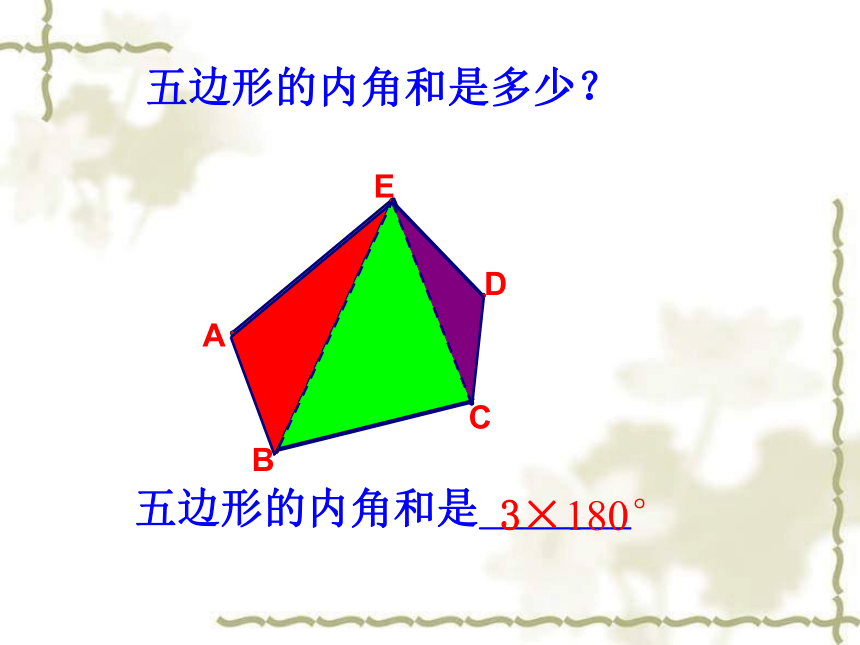
五边形的内角和是多少?
五边形的内角和是_______
3×180°
F
A
B
C
D
E
六边形的内角和是多少?
六边形的内角和是________
4×180°
归纳推理
多边形边数
从一个顶点引出对角线数
图形
分割成的三角形个数
多边形的内角和
4
5
6
...
……
……
……
……
n
2
2× 180°
3
3× 180°
4
4× 180°
n-2
(n-2) ?180°
1
2
3
n-3
n边形的内角和公式:
(n-2)?180°
结论:
(n≥3, n为整数)
探索多边形的内角和关键是:
把多边形分成几个三角形,再利用三角形的内角和求得。
议
一
议
P
A
E
D
C
B
A
E
D
C
B
P
5×180o-360o
4×180o-180o
例2
已知多边形的每一内角为150°,求这个多边形的边数.
解
设这个多边形的边数为n,
根据题意,得
(n-2)× 180° = 150° n
解这个方程,得n= 12
经检验,符合题意
答:这个多边形的边数为12.
八边形的内角和是 ;
例1
1080o
应用公式解题:
二、精设练习 巩固新知
1、求下列图形中 x的值
140°
x°
x°
90°
2x °
150 °
120 °
x °
X°
80 °
75 °
120 °
3.四边形的内角的度数之比为2∶3∶5∶8,则各角度数为 .
2、多边形内角和为1620°则它为_____边形,
多边形每个内角都 等于120°,则它为_____边形。
三、应用新知
1、如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,如何知道模板是否合格?为什么?
2、有一把锋利的“小刀”,把你的课桌(四边形)一个角削去,剩下的课桌是一个几边形?它的内角和是多少?
①
②
③
A
B
C
D
E
F
M
N
概念
边
角(内角和外角)
顶点
对角线
多边形的内角和
(n-2) · 180°
多边形
类比、转化、归纳的数学思想方法.
华东师大版《数学》七年级下册
类比
1、你能说一说什么叫三角形?
2、你能说出什么叫四边形、五边形、多边形吗?
3、你能说出多边形的顶点、边、内角、外角吗?
一、探究新知
问题:
我们现在研究的是如图9.2.1所示的多边形,是凸多边形; 如图9.2.2所示的多边形,是凹多边形,但不在现在研究的范围中。今后如果不说明,我们讲的多边形都是凸多边形。
图 9.2.2
比
一
比
注意:
图
9.2.1
三条边都相等,三个角也都相等
如果多边形各边都相等,各个角也都相等,那么这样的多边形就叫做正多边形。
正三角形
正四边形
正五边形
正六边形
正八边形
(等边三角形)
(正方形)
问题:
类比归纳:
什么叫正三角形?
画出连结下面四点的所有线段:
连结多边形不相邻的两个顶点的线段叫做多边形的对角线。
做
一
做
A
B
C
D
问题:
D
A
B
C
连接BD,把四边形ABCD分成2个三角形,将求四边形ABCD内角和的问题转化为求△ABD与△DCB的内角和。则四边形的内角和是_____
任意四边形的内角和是多少?
2×180°
问题:
E
A
B
C
D
五边形的内角和是多少?
五边形的内角和是_______
3×180°
F
A
B
C
D
E
六边形的内角和是多少?
六边形的内角和是________
4×180°
归纳推理
多边形边数
从一个顶点引出对角线数
图形
分割成的三角形个数
多边形的内角和
4
5
6
...
……
……
……
……
n
2
2× 180°
3
3× 180°
4
4× 180°
n-2
(n-2) ?180°
1
2
3
n-3
n边形的内角和公式:
(n-2)?180°
结论:
(n≥3, n为整数)
探索多边形的内角和关键是:
把多边形分成几个三角形,再利用三角形的内角和求得。
议
一
议
P
A
E
D
C
B
A
E
D
C
B
P
5×180o-360o
4×180o-180o
例2
已知多边形的每一内角为150°,求这个多边形的边数.
解
设这个多边形的边数为n,
根据题意,得
(n-2)× 180° = 150° n
解这个方程,得n= 12
经检验,符合题意
答:这个多边形的边数为12.
八边形的内角和是 ;
例1
1080o
应用公式解题:
二、精设练习 巩固新知
1、求下列图形中 x的值
140°
x°
x°
90°
2x °
150 °
120 °
x °
X°
80 °
75 °
120 °
3.四边形的内角的度数之比为2∶3∶5∶8,则各角度数为 .
2、多边形内角和为1620°则它为_____边形,
多边形每个内角都 等于120°,则它为_____边形。
三、应用新知
1、如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,如何知道模板是否合格?为什么?
2、有一把锋利的“小刀”,把你的课桌(四边形)一个角削去,剩下的课桌是一个几边形?它的内角和是多少?
①
②
③
A
B
C
D
E
F
M
N
概念
边
角(内角和外角)
顶点
对角线
多边形的内角和
(n-2) · 180°
多边形
类比、转化、归纳的数学思想方法.
