华东师大版七年级下册 10.3 旋转 第1课时 图形的旋转 课件(共20张PPT)
文档属性
| 名称 | 华东师大版七年级下册 10.3 旋转 第1课时 图形的旋转 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 10.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 17:19:50 | ||
图片预览







文档简介
一、问题情景,温故新知
二、情景激凝,导入新课
三、探究发现,认识旋转
四、归纳总结
五、学以致用
六、经典数学
温故知新
1.什么是轴对称?轴对称有什么性质?
一个图形沿某条直线翻折后能与另一个图形完全重合,那么这两个图形成轴对称,简称轴对称。
温故知新
2.什么是平移?平移有什么特征?平移与轴对称有什么共性?
A
B
C
A′
B′
C′
平面内一个图形沿着某个方向移动一定的距离叫做平移。
生活中还有其他图形变换吗?
情境激疑
在画中,你发现了什么?它们有哪些共同的特征?
形状和大小改变吗?
B
O
A
45°
探究发现
认识旋转1 –点的旋转
点A绕__点,往___方向,转动了__度到点B.
O
顺时针
45
探究发现
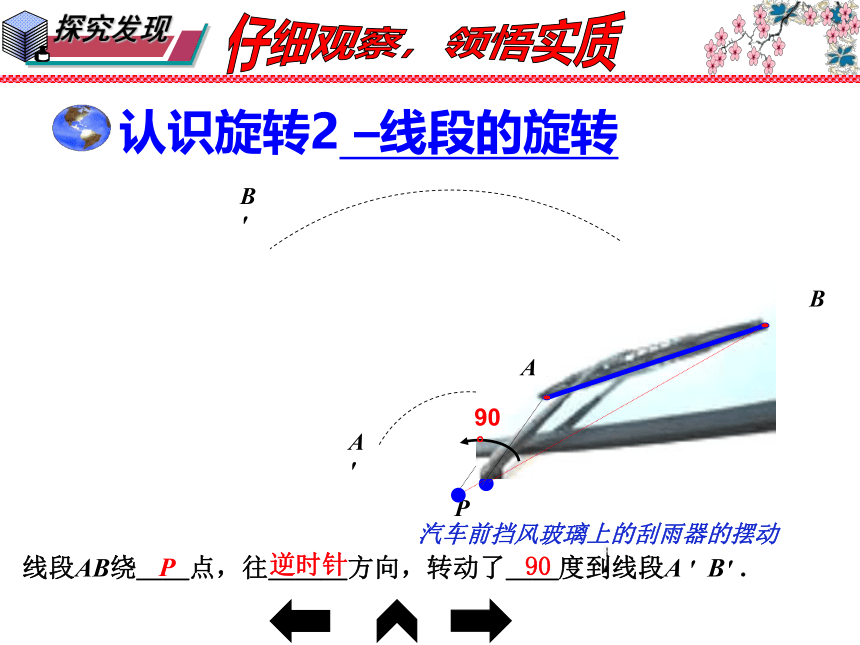
认识旋转2 –线段的旋转
P
B
A
B'
A'
90°
线段AB绕__点,往___方向,转动了__度到线段A ' B' .
P
逆时针
90
汽车前挡风玻璃上的刮雨器的摆动
探究发现
认识旋转3 –图形的旋转
B
A
B '
A '
C
C?
O
100°
旋转中心
旋转角度
旋转方向
1.旋转的三要素:
△ABC绕__点,往___方向,转动了__度到△A'B 'C' .
O
顺时针
100
2.旋转改变了图形的位置和方向,但图形的形状和大小不变。
旋转必须满足什么条件?
旋转的实质是什么?
归纳总结
转动的角∠AOB称为旋转角
在平面内,将一个图形绕着一定定点沿某个方向转动一个角度,
这样的图形运动称为旋转。
这个定点O称为旋转中心
旋转角
旋转中心
A
O
B
转动的角∠AOB称为旋转角
P
P’
如果图形上的 经过旋转变为 ,那么这 叫做这个旋转的 。
OP
OP’
对应线段
两条线段
任意一对对应点与旋转中心的连线所成的角都是旋转角。
图形旋转的三要素:
旋转中心、旋转角度、旋转方向.
从旋转中可以看到点A旋转到点A′,OA旋转到O A′,∠AOB
旋转到∠A′OB′.
O
A
B
A′
B′
45°
45°
(1)点B的对应点是( )
(2)线段OA的对应线段分别是( )
(3)线段AB的对应线段是( )
(4)∠A的对应角是( )
(5)∠B的对应角是( )
(6)旋转中心是( )
(7)旋转的角度是( )
B′
O A′
∠ A′
∠ B′
点O
45°
A B′
我们把点A与点A′叫做对应点,OA与O A′叫做对应线段,
∠AOB与
∠A′OB′叫做对应角。
根据刚才的旋转,完成下列填空:
从刚才的探究中发现:△AOB绕点O旋转45°得到△ A′O B′
O
A
B
A′
B′
45°
45°
思考并解决下列问题:
(1)指出图中的旋转中心,旋转角,对应线段;
(2)旋转角,对应线段有什么样的数量关系?
旋转中心在图形上哟!
如果旋转中心在△ABC外的点O处,逆时针旋转60°,将△ABC旋转到△A′B′C′的位置,则这两个三角形的顶点、边与角又有何种关系?
A′
A
O
B′
C′
B
C
例 1
如图,?ABC是等边三角形,D是BC上一点,?ABD经过旋转后
到达
?ACE 的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
A
B
C
D
E
M
解:(1)旋转中心是点A;
(2)旋转了60°;
(3)点M转到了AC的中点位置上。
思考
(1)图中的旋转角有哪些?等于多少度?
(2)连结DE,那么?ADE是什么形状的三角形?
∠BAC和∠DAE都是旋转角,都等于60°
等腰直角三角形
若将等边三角形替换为正方形呢?
学以致用
学以致用
例 2
如图,E是正方形ABCD边DC上一点,将?ADE旋转到?ABF.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)连结FE,试问?ADE是什么三角形,并说明理由?
解:(1)旋转中心是点A;
(2)旋转了90°;
A
B
C
D
E
F
(3)?ADE是等腰直角三角形。
数 学 活 动 室
经 典 数 学
1.如图,如果把钟表的指针看做四边形AOBC,它绕着O点旋转得到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么?
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
C
A
B
O
E
F
D
1、旋转中心是O
2、点D和点E的位置
4、AO=DO
BO=EO
5、∠AOD=∠BOE
3、∠AOD和∠BOE都是旋转角
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
习题 10.3
P 121
第1、2题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
二、情景激凝,导入新课
三、探究发现,认识旋转
四、归纳总结
五、学以致用
六、经典数学
温故知新
1.什么是轴对称?轴对称有什么性质?
一个图形沿某条直线翻折后能与另一个图形完全重合,那么这两个图形成轴对称,简称轴对称。
温故知新
2.什么是平移?平移有什么特征?平移与轴对称有什么共性?
A
B
C
A′
B′
C′
平面内一个图形沿着某个方向移动一定的距离叫做平移。
生活中还有其他图形变换吗?
情境激疑
在画中,你发现了什么?它们有哪些共同的特征?
形状和大小改变吗?
B
O
A
45°
探究发现
认识旋转1 –点的旋转
点A绕__点,往___方向,转动了__度到点B.
O
顺时针
45
探究发现
认识旋转2 –线段的旋转
P
B
A
B'
A'
90°
线段AB绕__点,往___方向,转动了__度到线段A ' B' .
P
逆时针
90
汽车前挡风玻璃上的刮雨器的摆动
探究发现
认识旋转3 –图形的旋转
B
A
B '
A '
C
C?
O
100°
旋转中心
旋转角度
旋转方向
1.旋转的三要素:
△ABC绕__点,往___方向,转动了__度到△A'B 'C' .
O
顺时针
100
2.旋转改变了图形的位置和方向,但图形的形状和大小不变。
旋转必须满足什么条件?
旋转的实质是什么?
归纳总结
转动的角∠AOB称为旋转角
在平面内,将一个图形绕着一定定点沿某个方向转动一个角度,
这样的图形运动称为旋转。
这个定点O称为旋转中心
旋转角
旋转中心
A
O
B
转动的角∠AOB称为旋转角
P
P’
如果图形上的 经过旋转变为 ,那么这 叫做这个旋转的 。
OP
OP’
对应线段
两条线段
任意一对对应点与旋转中心的连线所成的角都是旋转角。
图形旋转的三要素:
旋转中心、旋转角度、旋转方向.
从旋转中可以看到点A旋转到点A′,OA旋转到O A′,∠AOB
旋转到∠A′OB′.
O
A
B
A′
B′
45°
45°
(1)点B的对应点是( )
(2)线段OA的对应线段分别是( )
(3)线段AB的对应线段是( )
(4)∠A的对应角是( )
(5)∠B的对应角是( )
(6)旋转中心是( )
(7)旋转的角度是( )
B′
O A′
∠ A′
∠ B′
点O
45°
A B′
我们把点A与点A′叫做对应点,OA与O A′叫做对应线段,
∠AOB与
∠A′OB′叫做对应角。
根据刚才的旋转,完成下列填空:
从刚才的探究中发现:△AOB绕点O旋转45°得到△ A′O B′
O
A
B
A′
B′
45°
45°
思考并解决下列问题:
(1)指出图中的旋转中心,旋转角,对应线段;
(2)旋转角,对应线段有什么样的数量关系?
旋转中心在图形上哟!
如果旋转中心在△ABC外的点O处,逆时针旋转60°,将△ABC旋转到△A′B′C′的位置,则这两个三角形的顶点、边与角又有何种关系?
A′
A
O
B′
C′
B
C
例 1
如图,?ABC是等边三角形,D是BC上一点,?ABD经过旋转后
到达
?ACE 的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
A
B
C
D
E
M
解:(1)旋转中心是点A;
(2)旋转了60°;
(3)点M转到了AC的中点位置上。
思考
(1)图中的旋转角有哪些?等于多少度?
(2)连结DE,那么?ADE是什么形状的三角形?
∠BAC和∠DAE都是旋转角,都等于60°
等腰直角三角形
若将等边三角形替换为正方形呢?
学以致用
学以致用
例 2
如图,E是正方形ABCD边DC上一点,将?ADE旋转到?ABF.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)连结FE,试问?ADE是什么三角形,并说明理由?
解:(1)旋转中心是点A;
(2)旋转了90°;
A
B
C
D
E
F
(3)?ADE是等腰直角三角形。
数 学 活 动 室
经 典 数 学
1.如图,如果把钟表的指针看做四边形AOBC,它绕着O点旋转得到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么?
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
C
A
B
O
E
F
D
1、旋转中心是O
2、点D和点E的位置
4、AO=DO
BO=EO
5、∠AOD=∠BOE
3、∠AOD和∠BOE都是旋转角
我的收获是……
这节课我学到了什么?
我还有……的疑惑
小 结
习题 10.3
P 121
第1、2题
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
