华东师大版七年级下册数学 9.1 认识三角形 课件(22张PPT )
文档属性
| 名称 | 华东师大版七年级下册数学 9.1 认识三角形 课件(22张PPT ) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 00:00:00 | ||
图片预览






文档简介
通过欣赏以上图片,首先映入眼帘的是哪一种基本图案?
答:三角形
9.1.1 认识三角形
1.认识三角形的各部分组成以及它们的表示方法。
2.了解三角形的两种分类。
3.理解三角形的中线、角平分线和高。
4.清楚三角形中三种线的交点位置。
学习目标
定义理解
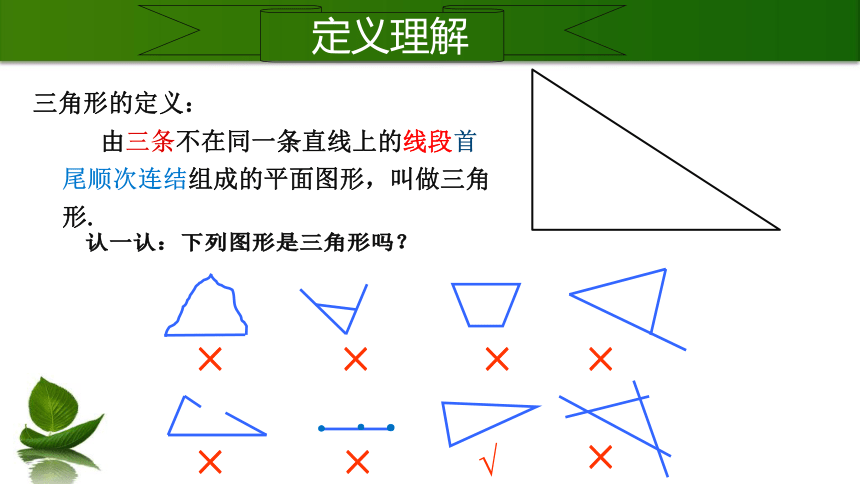
三角形的定义:
由三条不在同一条直线上的线段首尾顺次连结组成的平面图形,叫做三角形.
认一认:下列图形是三角形吗?
×
×
×
√
×
×
×
×
·
·
·
学习新知
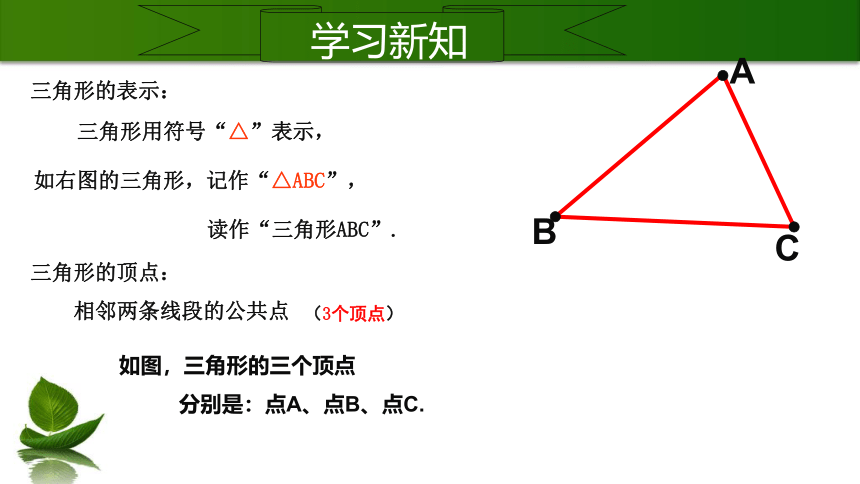
三角形的表示:
三角形用符号“△”表示,
如右图的三角形,记作“△ABC”,
读作“三角形ABC”.
A
B
C
三角形的顶点:
相邻两条线段的公共点
如图,三角形的三个顶点
分别是:点A、点B、点C.
(3个顶点)
学习新知
A
B
C
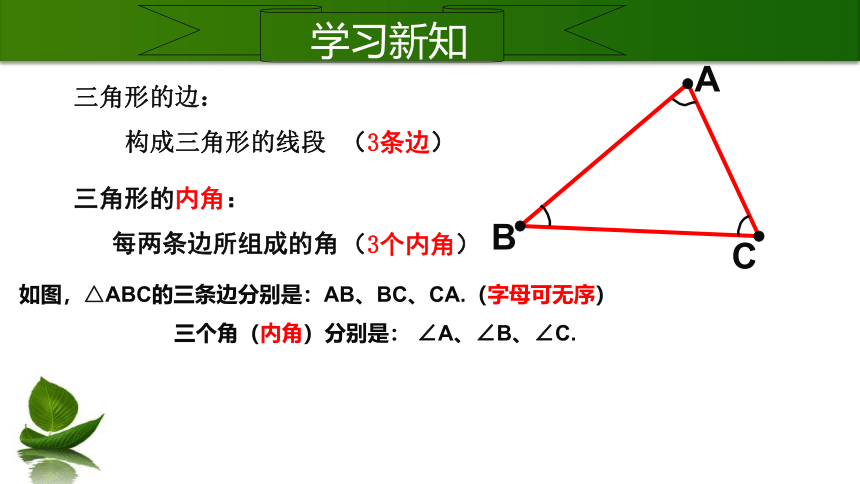
如图,△ABC的三条边分别是:AB、BC、CA.(字母可无序)
三个角(内角)分别是: ∠A、∠B、∠C.
三角形的边:
构成三角形的线段
(3条边)
三角形的内角:
每两条边所组成的角
(3个内角)
学习新知
A
B
C
D
三角形中内角的一边与另一边的反向延长线所组成的角叫做三角形的外角.
如图,∠ACD是△ABC的一个外角
三角形的外角:
想一想:
一个三角形有多少个外角呢?这些外角又会存在什么关系呢?
三角形的外角与它相邻的内角互为邻补角.
画一个△ABC ,你能画出它的所有外角吗?
请动手试一试.
.
.
.
3
(
(
2
(
1
(
4
(
5
(
6
A
B
C
三角形的一个内角与它相邻的外角有两个,它们是对顶角.
实践操作
跟踪训练
A
B
C
D
E
1.请同学们表示出下图中的三角形,并写出它的顶点,边,内角,以及图中所示的外角。
三角形:△ABC。
顶点:点A、点B、点C。
边:AB、BC、CA。
内角:∠B、∠BAC、∠ACB。
外角:∠EAC、∠ACD。
跟踪训练
2.如图所示,点D是AC上一点,点E是BD上一点,则下列说法正确的是( )
D.∠2不是△EDC的外角
C.∠1是△BEC的外角
B.∠1是△ABD的外角
A.∠2是△ABD的外角
B
A
B
C
D
E
2
1
3.图中以BC为边的三角形共有______个;它们分别是
______________________________ .
在△ABD中,∠A是_______边的对角, ∠ADB是△ 的内角,又是 的一个外角.
D
B
E
C
F
A
4
△BCF,△BCE,△BCD,△BCA
△FDC 或△BDC
ABD
BD
跟踪训练
三角形的分类
按角分类
锐角三角形
直角三角形
钝角三角形
等腰三角形
三条边相等的等边三角形
不等边三角形(不规则三角形)
按边分类
两条边相等的等腰三角形
三角形的角平分线
三角形的角平分线是一条线段,线段的长度为顶点与内角平分线和对边交线间的距离。
作法:作△ABC的内角∠BAC的平分线交对边BC与点D,线段AD就是△ABC的一条平分线。
如图1中的AD为∠BAC的角平分线,BE为∠ABC的角平分线,CF为∠BCA的角平分线,这些都是线段,并且处于三角形的内部。
角平分线
中线
三角形的中线
三角形的中线也是一条线段,线段的长度为顶点到对边中点间的距离。
作法:取△ABC边BC的中点D,连接AD,线段AD就是△ABC的一条中线。
如图2中,AD、BE、CF均为三角形的中线,这些也都是线段,并且均处于三角形的内部。
高
三角形的高
三角形的高线也是一条线段,线段的长度顶点到对边的距离,也就是从顶点向对边(对边的延长线)做垂线,垂线段的长度就是高的大小。
作法:过三角形的顶点,作对边的垂线段。
如图3-1所示,AD、CF、BE均为三角形的高,此时高在三角形的内部;如图3-2所示,AC、BC、CD为三角形的高,此时有两条高为三角形的边线;如图3-3所示,AD、CF、BE为三角形的高,此时有两条高在三角形的外部。
三线交点
由上面的学习,我们可以发现,三角形的三条中线、三条角平分线和三条高(所在的直线)分别相交于一点;其中,三角形的三条中线、三条角平分线和锐角三角形三条高的交点都在三角形的内部;而直角三角形三条高的交点就是直角顶点;钝角三角形有两条高位于三角形的外部,因此三条高的交点在它们所在的直线上。
自我反思
课本P75:
练 习 第1.2题
课本P76:
练 习 第1.2题
请同学们认真完成!!!
课后作业
再见
答:三角形
9.1.1 认识三角形
1.认识三角形的各部分组成以及它们的表示方法。
2.了解三角形的两种分类。
3.理解三角形的中线、角平分线和高。
4.清楚三角形中三种线的交点位置。
学习目标
定义理解
三角形的定义:
由三条不在同一条直线上的线段首尾顺次连结组成的平面图形,叫做三角形.
认一认:下列图形是三角形吗?
×
×
×
√
×
×
×
×
·
·
·
学习新知
三角形的表示:
三角形用符号“△”表示,
如右图的三角形,记作“△ABC”,
读作“三角形ABC”.
A
B
C
三角形的顶点:
相邻两条线段的公共点
如图,三角形的三个顶点
分别是:点A、点B、点C.
(3个顶点)
学习新知
A
B
C
如图,△ABC的三条边分别是:AB、BC、CA.(字母可无序)
三个角(内角)分别是: ∠A、∠B、∠C.
三角形的边:
构成三角形的线段
(3条边)
三角形的内角:
每两条边所组成的角
(3个内角)
学习新知
A
B
C
D
三角形中内角的一边与另一边的反向延长线所组成的角叫做三角形的外角.
如图,∠ACD是△ABC的一个外角
三角形的外角:
想一想:
一个三角形有多少个外角呢?这些外角又会存在什么关系呢?
三角形的外角与它相邻的内角互为邻补角.
画一个△ABC ,你能画出它的所有外角吗?
请动手试一试.
.
.
.
3
(
(
2
(
1
(
4
(
5
(
6
A
B
C
三角形的一个内角与它相邻的外角有两个,它们是对顶角.
实践操作
跟踪训练
A
B
C
D
E
1.请同学们表示出下图中的三角形,并写出它的顶点,边,内角,以及图中所示的外角。
三角形:△ABC。
顶点:点A、点B、点C。
边:AB、BC、CA。
内角:∠B、∠BAC、∠ACB。
外角:∠EAC、∠ACD。
跟踪训练
2.如图所示,点D是AC上一点,点E是BD上一点,则下列说法正确的是( )
D.∠2不是△EDC的外角
C.∠1是△BEC的外角
B.∠1是△ABD的外角
A.∠2是△ABD的外角
B
A
B
C
D
E
2
1
3.图中以BC为边的三角形共有______个;它们分别是
______________________________ .
在△ABD中,∠A是_______边的对角, ∠ADB是△ 的内角,又是 的一个外角.
D
B
E
C
F
A
4
△BCF,△BCE,△BCD,△BCA
△FDC 或△BDC
ABD
BD
跟踪训练
三角形的分类
按角分类
锐角三角形
直角三角形
钝角三角形
等腰三角形
三条边相等的等边三角形
不等边三角形(不规则三角形)
按边分类
两条边相等的等腰三角形
三角形的角平分线
三角形的角平分线是一条线段,线段的长度为顶点与内角平分线和对边交线间的距离。
作法:作△ABC的内角∠BAC的平分线交对边BC与点D,线段AD就是△ABC的一条平分线。
如图1中的AD为∠BAC的角平分线,BE为∠ABC的角平分线,CF为∠BCA的角平分线,这些都是线段,并且处于三角形的内部。
角平分线
中线
三角形的中线
三角形的中线也是一条线段,线段的长度为顶点到对边中点间的距离。
作法:取△ABC边BC的中点D,连接AD,线段AD就是△ABC的一条中线。
如图2中,AD、BE、CF均为三角形的中线,这些也都是线段,并且均处于三角形的内部。
高
三角形的高
三角形的高线也是一条线段,线段的长度顶点到对边的距离,也就是从顶点向对边(对边的延长线)做垂线,垂线段的长度就是高的大小。
作法:过三角形的顶点,作对边的垂线段。
如图3-1所示,AD、CF、BE均为三角形的高,此时高在三角形的内部;如图3-2所示,AC、BC、CD为三角形的高,此时有两条高为三角形的边线;如图3-3所示,AD、CF、BE为三角形的高,此时有两条高在三角形的外部。
三线交点
由上面的学习,我们可以发现,三角形的三条中线、三条角平分线和三条高(所在的直线)分别相交于一点;其中,三角形的三条中线、三条角平分线和锐角三角形三条高的交点都在三角形的内部;而直角三角形三条高的交点就是直角顶点;钝角三角形有两条高位于三角形的外部,因此三条高的交点在它们所在的直线上。
自我反思
课本P75:
练 习 第1.2题
课本P76:
练 习 第1.2题
请同学们认真完成!!!
课后作业
再见
