华东师大版七年级下册数学课件:7.2 加减法解二元一次方程组 (共16张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学课件:7.2 加减法解二元一次方程组 (共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 870.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 10:55:18 | ||
图片预览






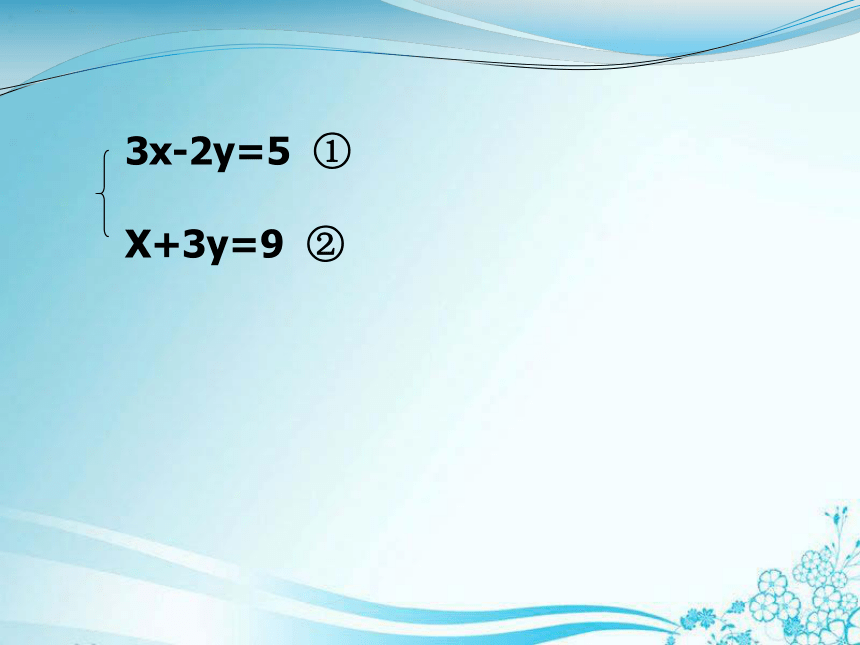
文档简介
学习目标:
1.掌握用加减法解二元一次方程组的步骤。
2.熟练运用加减法解二元一次方程组。
3.培养分析问题、解决问题的能力。
重点、难点
准确地选择加法或减法进行消元
设疑自探:
问题:
1、什么是加减消元法?
2、什么条件下用加法、什么条件下用减法?
观察:此方程组中,
(1)未知数 x 的系数有什么特点?
(2)怎么样才能把这个未知数x消去?
3x + 5y = 5 (1)
3x - 4y =23 (2)
☆ 加减消元法:
例1、解方程组
3x + 5y = 5
3x - 4y =23
①
②
解:
把 ① - ② 得
(3x + 5y) – (3x – 4y ) = 5 - 23
3x + 5y - 3x + 4y = - 18
9y = -18
y = - 2
把 y = - 2 代入 ① , 得
3x + 5 × ( - 2 ) = 5
解得
x = 5
所以,原方程组的解是
x = 5
y = - 2
。
例2、解方程组
3x + 7y = 9
4x - 7y = 5
①
②
解:
把 ① + ②,得
(3x + 7y ) + ( 4x - 7y ) = 9 + 5
3x + 7y + 4x - 7y = 14
7x = 14
x = 2
把 x = 2 代入 ① ,得
3 ×2 + 7y = 9
y =
所以,原方程组的解是
x = 2
y =
3x-2y=5 ①
X+3y=9 ②
归纳:通过以上两个例子:
将两个方程相加(或相减),
消去一个未知数,
将方程组转化为一元一次方程来解,
这种解法叫做加减消元法,
简称加减法。
主要步骤:
基本思路:
求解
加减
二元
一元
加减消元:
消去一个未知数
求出两个未知数的值
归纳 :
加减消元法解方程组基本思路、主要步骤:
变形
同一个未知数的系数相同,用减法消元,互为相反数时,用加法消元
代入法、加减法
分别相加
y
1.已知方程组
x+3y=17
2x-3y=6
两个方程只要两边
就可以消去未知数
分别相减
2.已知方程组
25x-7y=16
25x+6y=10
两个方程只要两边
就可以消去未知数
x
3.已知a、b满足方程组
a+2b=8
2a+b=7
则a+b=
5
二.选择题
1. 用加减法解方程组
6x+7y=-19①
6x-5y=17②
应用( )
A.①-②消去y
B.①-②消去x
B. ②- ①消去常数项
D. 以上都不对
B
2.方程组
3x+2y=13
3x-2y=5
消去y后所得的方程是( )
B
A.6x=8
B.6x=18
C.6x=5
D.x=18
1、
3x2a+b+2
+5y3a-b+1=8
是关于x、y的二元一次方程
求a、b。
解:根据题意:得
2a+b+2=1
3a-b+1=1
解得:
a=
b=
1
5
-
3
5
-
思维升级
2、已知3a3xb2x-y和-7a8-yb7是同类项,求x·y的值。
解:根据题意:得
3x=8-y
2x-y=7
转化为
3x+y=8
2x-y=7
x=3
y=-1
解得:
即xy=-3
3、已知(3m+2n-16)2与|3m-n-1|互为相反数
求:m+n的值
解:根据题意:得
3m+2n-16=0
3m-n-1=0
解得:
m=2
n=5
即:m+n=7
已知关于x,y的方程组的解
满足x+y=4,求a的值.
3x+2y=a+2
2X+3y=2a
6.
5 、 已知方程组{
ax-by=4
ax+by=2
与方程组{
4x+3y=4
4x-5y=6
的解相同,求a,b
小结与回顾
学习了二元一次方程组的另一种方法——加减法消元法。它是通过把两个方程两边相加(或相减)消去一个未知数,把二元一次方程组转化为一元一次方程。
二元一次方程
一元一次方程
消元
转化
1.掌握用加减法解二元一次方程组的步骤。
2.熟练运用加减法解二元一次方程组。
3.培养分析问题、解决问题的能力。
重点、难点
准确地选择加法或减法进行消元
设疑自探:
问题:
1、什么是加减消元法?
2、什么条件下用加法、什么条件下用减法?
观察:此方程组中,
(1)未知数 x 的系数有什么特点?
(2)怎么样才能把这个未知数x消去?
3x + 5y = 5 (1)
3x - 4y =23 (2)
☆ 加减消元法:
例1、解方程组
3x + 5y = 5
3x - 4y =23
①
②
解:
把 ① - ② 得
(3x + 5y) – (3x – 4y ) = 5 - 23
3x + 5y - 3x + 4y = - 18
9y = -18
y = - 2
把 y = - 2 代入 ① , 得
3x + 5 × ( - 2 ) = 5
解得
x = 5
所以,原方程组的解是
x = 5
y = - 2
。
例2、解方程组
3x + 7y = 9
4x - 7y = 5
①
②
解:
把 ① + ②,得
(3x + 7y ) + ( 4x - 7y ) = 9 + 5
3x + 7y + 4x - 7y = 14
7x = 14
x = 2
把 x = 2 代入 ① ,得
3 ×2 + 7y = 9
y =
所以,原方程组的解是
x = 2
y =
3x-2y=5 ①
X+3y=9 ②
归纳:通过以上两个例子:
将两个方程相加(或相减),
消去一个未知数,
将方程组转化为一元一次方程来解,
这种解法叫做加减消元法,
简称加减法。
主要步骤:
基本思路:
求解
加减
二元
一元
加减消元:
消去一个未知数
求出两个未知数的值
归纳 :
加减消元法解方程组基本思路、主要步骤:
变形
同一个未知数的系数相同,用减法消元,互为相反数时,用加法消元
代入法、加减法
分别相加
y
1.已知方程组
x+3y=17
2x-3y=6
两个方程只要两边
就可以消去未知数
分别相减
2.已知方程组
25x-7y=16
25x+6y=10
两个方程只要两边
就可以消去未知数
x
3.已知a、b满足方程组
a+2b=8
2a+b=7
则a+b=
5
二.选择题
1. 用加减法解方程组
6x+7y=-19①
6x-5y=17②
应用( )
A.①-②消去y
B.①-②消去x
B. ②- ①消去常数项
D. 以上都不对
B
2.方程组
3x+2y=13
3x-2y=5
消去y后所得的方程是( )
B
A.6x=8
B.6x=18
C.6x=5
D.x=18
1、
3x2a+b+2
+5y3a-b+1=8
是关于x、y的二元一次方程
求a、b。
解:根据题意:得
2a+b+2=1
3a-b+1=1
解得:
a=
b=
1
5
-
3
5
-
思维升级
2、已知3a3xb2x-y和-7a8-yb7是同类项,求x·y的值。
解:根据题意:得
3x=8-y
2x-y=7
转化为
3x+y=8
2x-y=7
x=3
y=-1
解得:
即xy=-3
3、已知(3m+2n-16)2与|3m-n-1|互为相反数
求:m+n的值
解:根据题意:得
3m+2n-16=0
3m-n-1=0
解得:
m=2
n=5
即:m+n=7
已知关于x,y的方程组的解
满足x+y=4,求a的值.
3x+2y=a+2
2X+3y=2a
6.
5 、 已知方程组{
ax-by=4
ax+by=2
与方程组{
4x+3y=4
4x-5y=6
的解相同,求a,b
小结与回顾
学习了二元一次方程组的另一种方法——加减法消元法。它是通过把两个方程两边相加(或相减)消去一个未知数,把二元一次方程组转化为一元一次方程。
二元一次方程
一元一次方程
消元
转化
