华东师大版七年级下册数学:9.1.3 三角形的三边关系(共26张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学:9.1.3 三角形的三边关系(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 17:22:25 | ||
图片预览







文档简介
三角形的三边关系
1.掌握三角形三条边之间的关系;
2.会应用三角形三边关系处理问题;
3.了解三角形的稳定性.
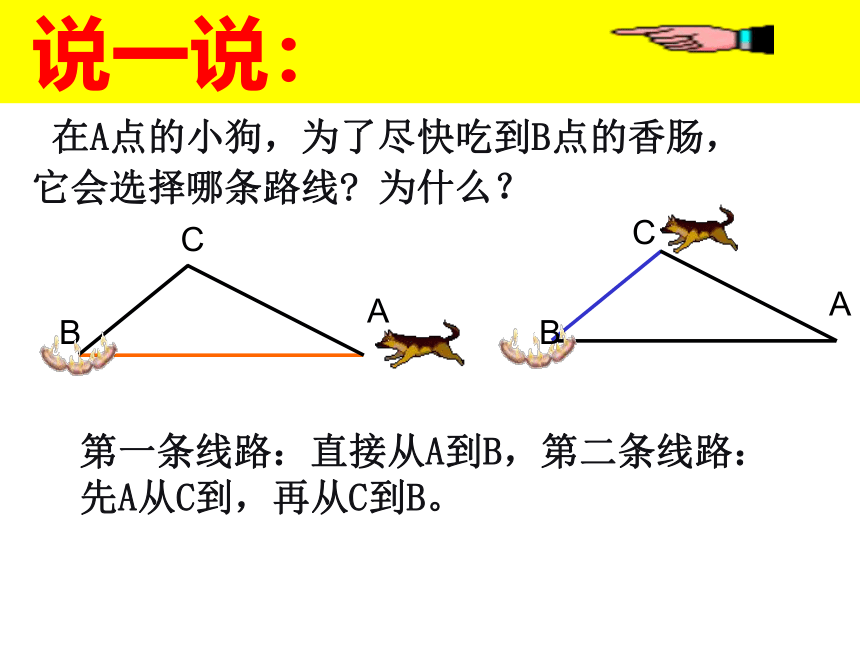
说一说:
在A点的小狗,为了尽快吃到B点的香肠,它会选择哪条路线? 为什么?
B
C
A
C
A
B
第一条线路:直接从A到B,第二条线路:先A从C到,再从C到B。
C
A
B
a
c
b
在刚才的问题中,把路线1看成边长c,路线2看成边长a+b,则a+b与c有什么关系?a+c与b呢?b+c与a呢?由此你能得出什么结论?
a+b>c a+c>b b+c>a
三角形的任意两边之和大于第三边
三角形较短两边之和大于第三边。
10 cm、15 cm、20cm 、 25cm.
小组活动:
从下列长度的线段中任意取三段能否组成一个三角形?
动手实践:
先想一想有几种取法?
简便方法
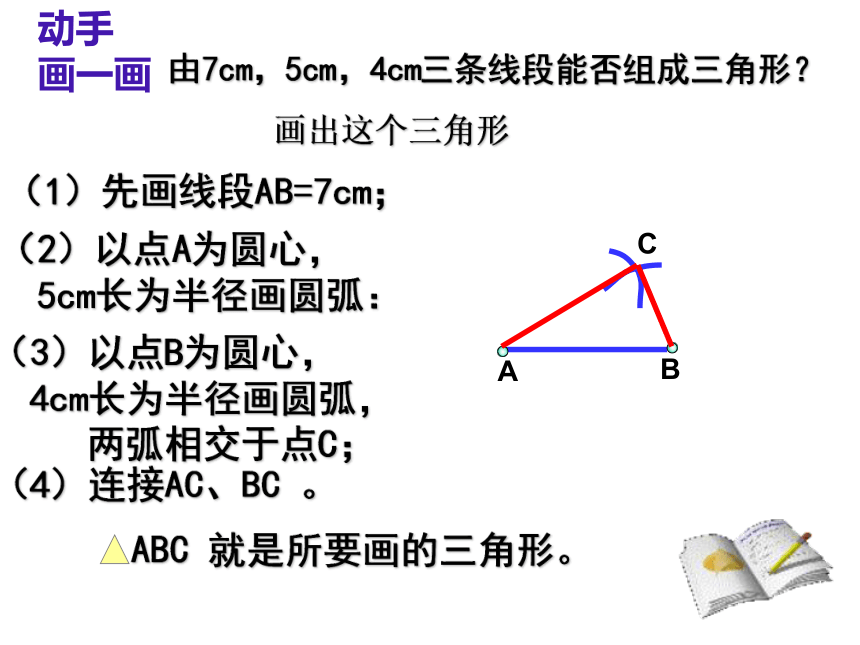
由7cm,5cm,4cm三条线段能否组成三角形?
(1)先画线段AB=7cm;
(2)以点A为圆心,
5cm长为半径画圆弧:
A
B
(3)以点B为圆心,
4cm长为半径画圆弧,
两弧相交于点C;
(4)连接AC、BC 。
ABC 就是所要画的三角形。
C
动手 画一画
画出这个三角形
画一画
以下列长度的各组线段为边长,画一个三角形。
(1)6cm、4cm、5cm
(2)7cm、2cm、4cm
用什么工具可以画的既准确,又迅速?
能否画出三角形?
拓展
a+b>c a+c>b b+c>a
利用不等式的变形以上得到的结论还能怎么表示?
如:c-a c-b即:三角形任意两边之差小于第三边
概括
1.三角形的任意两边之和大于第三边
2.三角形的任意两边之差小于第三边
即:两边只差<第三边<两边之和
1.判断下列长度的各组线段能否组成三角形?
(1)15cm、10cm、7cm
(2)4cm、5cm、10cm
(3)3cm、8cm、5cm
(4)4cm、5cm、6cm
知识应用:
实践篇
2.两根木棒的长分别为7cm、10cm,要选择第三根木棒,用它们钉成一个三角架,第三根木棒的长有什么限制?
3<第三边<17
3.已知;两条线段a、b,其长度分别为2.5cm与3.5cm,另有长度分别为1cm、3cm、5cm、7cm、9cm的5条线段,其中能够与线段a、b一起组成三角形的有哪几条?
4.已知△ABC是等腰三角形。
(1)如果它的两条边的长分别为8cm和3cm,那么它的周长是多少?
(2)如果它的周长为18cm,一条边的长为8cm,那么腰长是多少?
19cm
8cm或5cm
1.三角形的三边确定了三角形的形状和大
小就完全确定了;这个性质叫做三角形的
稳定性。
2.四边形有这个性质吗?
3.你能举出三角形的稳定性在生产、
生活中应用的例子吗?
说一说
在日常生活中三角形稳定性有什么应用?
想一想
要使下列木架稳定各至少需要多少根木棍?
课堂小结:
3.三角形的稳定性.
2.三角形的三边关系.
1.已知三边画三角形.
1.下列各组数中,不可能成为一个三角形三边长的是( )
A.2、3、4 B.5、7、 7
C. 5、6、12 D.6、8、10
2.长度分别为2、7、x的三条线段能组成一个三角形,x的值可以( )
A.4 B.5 C.6 D.9
课堂检测:
3.下列图形中具有稳定性的是( )
正方形 B.长方形
C.直角三角形 D.平行四边形
4. 已知△ABC是等腰三角形,
且它的两条边的长分别为8cm
和3cm,那么它的周长是多少?
布置作业:
教材82页 练习第1、2题
教材82页 习题9.1第一题
如果三角形的周长为11,其中一边长为4,另外两边为整数,求这个三角形的最大边长。
1.掌握三角形三条边之间的关系;
2.会应用三角形三边关系处理问题;
3.了解三角形的稳定性.
说一说:
在A点的小狗,为了尽快吃到B点的香肠,它会选择哪条路线? 为什么?
B
C
A
C
A
B
第一条线路:直接从A到B,第二条线路:先A从C到,再从C到B。
C
A
B
a
c
b
在刚才的问题中,把路线1看成边长c,路线2看成边长a+b,则a+b与c有什么关系?a+c与b呢?b+c与a呢?由此你能得出什么结论?
a+b>c a+c>b b+c>a
三角形的任意两边之和大于第三边
三角形较短两边之和大于第三边。
10 cm、15 cm、20cm 、 25cm.
小组活动:
从下列长度的线段中任意取三段能否组成一个三角形?
动手实践:
先想一想有几种取法?
简便方法
由7cm,5cm,4cm三条线段能否组成三角形?
(1)先画线段AB=7cm;
(2)以点A为圆心,
5cm长为半径画圆弧:
A
B
(3)以点B为圆心,
4cm长为半径画圆弧,
两弧相交于点C;
(4)连接AC、BC 。
ABC 就是所要画的三角形。
C
动手 画一画
画出这个三角形
画一画
以下列长度的各组线段为边长,画一个三角形。
(1)6cm、4cm、5cm
(2)7cm、2cm、4cm
用什么工具可以画的既准确,又迅速?
能否画出三角形?
拓展
a+b>c a+c>b b+c>a
利用不等式的变形以上得到的结论还能怎么表示?
如:c-a c-b即:三角形任意两边之差小于第三边
概括
1.三角形的任意两边之和大于第三边
2.三角形的任意两边之差小于第三边
即:两边只差<第三边<两边之和
1.判断下列长度的各组线段能否组成三角形?
(1)15cm、10cm、7cm
(2)4cm、5cm、10cm
(3)3cm、8cm、5cm
(4)4cm、5cm、6cm
知识应用:
实践篇
2.两根木棒的长分别为7cm、10cm,要选择第三根木棒,用它们钉成一个三角架,第三根木棒的长有什么限制?
3<第三边<17
3.已知;两条线段a、b,其长度分别为2.5cm与3.5cm,另有长度分别为1cm、3cm、5cm、7cm、9cm的5条线段,其中能够与线段a、b一起组成三角形的有哪几条?
4.已知△ABC是等腰三角形。
(1)如果它的两条边的长分别为8cm和3cm,那么它的周长是多少?
(2)如果它的周长为18cm,一条边的长为8cm,那么腰长是多少?
19cm
8cm或5cm
1.三角形的三边确定了三角形的形状和大
小就完全确定了;这个性质叫做三角形的
稳定性。
2.四边形有这个性质吗?
3.你能举出三角形的稳定性在生产、
生活中应用的例子吗?
说一说
在日常生活中三角形稳定性有什么应用?
想一想
要使下列木架稳定各至少需要多少根木棍?
课堂小结:
3.三角形的稳定性.
2.三角形的三边关系.
1.已知三边画三角形.
1.下列各组数中,不可能成为一个三角形三边长的是( )
A.2、3、4 B.5、7、 7
C. 5、6、12 D.6、8、10
2.长度分别为2、7、x的三条线段能组成一个三角形,x的值可以( )
A.4 B.5 C.6 D.9
课堂检测:
3.下列图形中具有稳定性的是( )
正方形 B.长方形
C.直角三角形 D.平行四边形
4. 已知△ABC是等腰三角形,
且它的两条边的长分别为8cm
和3cm,那么它的周长是多少?
布置作业:
教材82页 练习第1、2题
教材82页 习题9.1第一题
如果三角形的周长为11,其中一边长为4,另外两边为整数,求这个三角形的最大边长。
