华东师大版七年级下册数学:9.1.3三角形的三边关系课件(共20张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学:9.1.3三角形的三边关系课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 889.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 17:27:49 | ||
图片预览







文档简介
有人说姚明一步能走3米,你相信吗?
姚明腿长1.28米
9.1.3三角形的三边关系
学习目标
1、理解并掌握三角形的三边关系。
2、会利用三角形的三边关系解决有关问题。
重点:三角形的三边关系。
难点:已知三角形的两边求第三边的范围。
自主学习(请同学们预习课本80—81页)
问题:
1、利用圆规和直尺画一个三角形,使它的三条边长分别为4cm、3cm、2.5cm.
2、三角形的三边具有什么关系?怎样的三条线段才能构成三角形?
3、已知三角形的两边如何求第三边的取值范围?
对学群学(请组长带领组员进行讨论)
问题:
1、利用圆规和直尺画一个三角形,使它的三条边长分别为4cm、3cm、2.5cm.
2、三角形的三边具有什么关系?怎样的三条线段才能构成三角形?
3、已知三角形的两边如何求第三边的取值范围?
展示交流
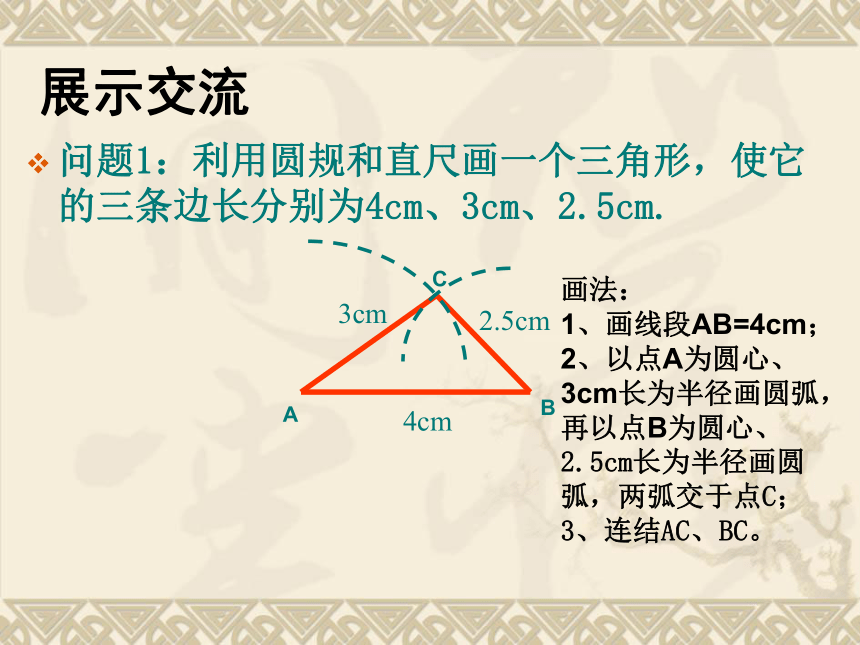
问题1:利用圆规和直尺画一个三角形,使它的三条边长分别为4cm、3cm、2.5cm.
4cm
3cm
2.5cm
A
C
B
画法:
1、画线段AB=4cm;
2、以点A为圆心、3cm长为半径画圆弧,再以点B为圆心、2.5cm长为半径画圆弧,两弧交于点C;
3、连结AC、BC。
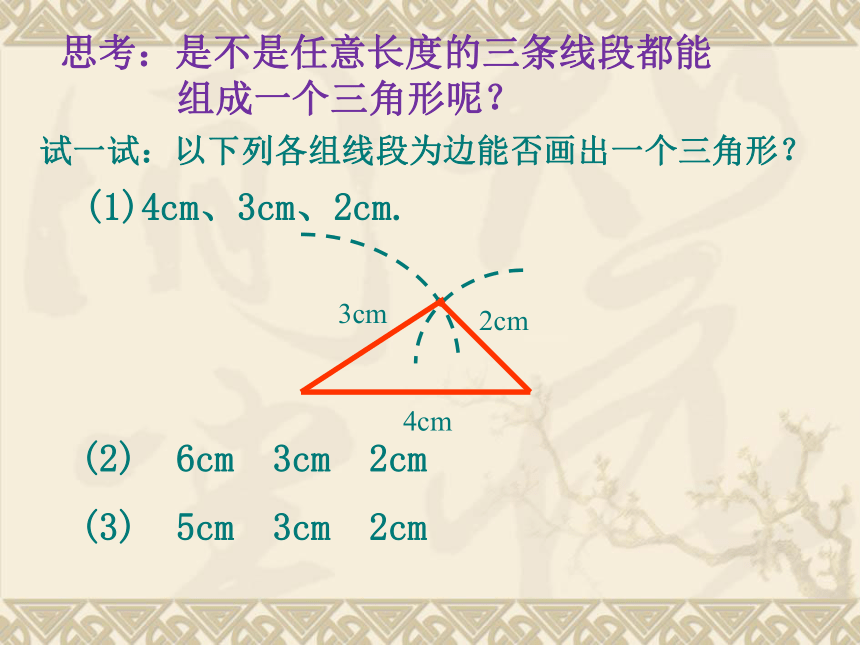
(1)4cm、3cm、2cm.
试一试:以下列各组线段为边能否画出一个三角形?
(2) 6cm 3cm 2cm
(3) 5cm 3cm 2cm
4cm
3cm
2cm
思考:是不是任意长度的三条线段都能
组成一个三角形呢?
(2) 6cm 、 3cm 、 2cm
3cm
6cm
2cm
(3) 5cm 、 3cm 、 2cm
3cm
2cm
5cm
(1) 4cm 、 3cm 、 2cm (可以)
(2) 6cm 、 3cm 、 2cm (不可以)
(3) 5cm 、 3cm 、 2cm (不可以)
通过画图,你能得到什么结论?
三角形的任何两边的和大于第三边
并不是任意三条线段都可以组成一个三角形。
在三条线段中,如果两条短线段的和不大于第三条线段,那么这三条线段就不能组成一个三角形。
三角形的三边关系
三角形的任何两边的和大于第三边。
探究交流
讨论:“任何”的含义?
利用此关系验证三条线段能否围成三角形时,只要判断较短的两条线段的和是否大于最长的线段即可。
(3)3 cm、8 cm、5 cm;
(4)4 cm、5 cm、6 cm.
(1) 15cm、10 cm、7 cm;
(2)4 cm、5 cm、10 cm;
下列长度的各组线段能否组成一个三角形?
小试牛刀
(5)a+1、a+2、a+3(a>0)
能
不能
不能
能
能
答:不能。如果此人一步能走3米,由三角形三边的关系得,此人两腿长之和要大于3米,这与实际情况相矛盾,所以他一步不能走3米。
姚明腿长1.28米
有人说他一步能走3米,你相信吗?能否用今天学过的知识去解答呢?
探究交流
探究1:已知M,N,P三点不在同一条直线上,且MN=4cm,NP=3cm,M,P两点间的距离为dcm,那么( )
A、5≤d≤7 B.1≤d≤5
C.d=5 D.1如果告诉你:
三角形两边的长度,
第三边长度的范围你能确定吗?
两边之差<第三边<两边之和
D
探究活动
一木工有两根长分别为40厘米和60厘米的木条,要另找一根木条,钉成一个三角木架。问第三根木条的长度应在什么范围内?
20厘米<第三根木条<100厘米
探究交流
探究2:已知?ABC是等腰三角形。
(1)如果它的两条边的长分别为8cm和3cm,那么它的周长是________cm;
(2)如果它的周长是18cm,一条边的长为4cm,那么它的腰长是________cm.
19
7
检测训练
1、若下列各组值代表线段的长度,则不能构成三角形的是( )
A、3,8,4 B、4,9,6
C、15,20,8 D、9,15,8
2、现有四根木棒,长度分别为4cm,6cm,8cm,10cm,从中任取三根木棒,能组成三角形的个数为( )
A、1个 B、2个 C、3个 D、4个
A
C
检测训练
3、在△ABC中,已知a、b、c是三角形的三边,a=8cm,b=2cm,则c的取值范围是 ;
4.一个等腰三角形的两边长分别为8cm和6cm,则它的周长为______________;
5、一个等腰三角形的两边长分别为2和7,则它的周长是_______.
6cm22cm或20cm
16
学生小结
通过这节课的学习,
你有哪些收获?
点评拓展
1、教师对本节课进行总评。
(1)三角形的三边关系
(2)判断三条线段能否组成三角形:采用一种较为简便的判法:若较短的两条边的和大于第三条边,则可构成三角形,否则不能.
(3)确定三角形第三边的取值范围:
两边之差<第三边<两边之和
(4)分类讨论等腰三角形的相关问题
2、拓展:
姚明腿长1.28米
9.1.3三角形的三边关系
学习目标
1、理解并掌握三角形的三边关系。
2、会利用三角形的三边关系解决有关问题。
重点:三角形的三边关系。
难点:已知三角形的两边求第三边的范围。
自主学习(请同学们预习课本80—81页)
问题:
1、利用圆规和直尺画一个三角形,使它的三条边长分别为4cm、3cm、2.5cm.
2、三角形的三边具有什么关系?怎样的三条线段才能构成三角形?
3、已知三角形的两边如何求第三边的取值范围?
对学群学(请组长带领组员进行讨论)
问题:
1、利用圆规和直尺画一个三角形,使它的三条边长分别为4cm、3cm、2.5cm.
2、三角形的三边具有什么关系?怎样的三条线段才能构成三角形?
3、已知三角形的两边如何求第三边的取值范围?
展示交流
问题1:利用圆规和直尺画一个三角形,使它的三条边长分别为4cm、3cm、2.5cm.
4cm
3cm
2.5cm
A
C
B
画法:
1、画线段AB=4cm;
2、以点A为圆心、3cm长为半径画圆弧,再以点B为圆心、2.5cm长为半径画圆弧,两弧交于点C;
3、连结AC、BC。
(1)4cm、3cm、2cm.
试一试:以下列各组线段为边能否画出一个三角形?
(2) 6cm 3cm 2cm
(3) 5cm 3cm 2cm
4cm
3cm
2cm
思考:是不是任意长度的三条线段都能
组成一个三角形呢?
(2) 6cm 、 3cm 、 2cm
3cm
6cm
2cm
(3) 5cm 、 3cm 、 2cm
3cm
2cm
5cm
(1) 4cm 、 3cm 、 2cm (可以)
(2) 6cm 、 3cm 、 2cm (不可以)
(3) 5cm 、 3cm 、 2cm (不可以)
通过画图,你能得到什么结论?
三角形的任何两边的和大于第三边
并不是任意三条线段都可以组成一个三角形。
在三条线段中,如果两条短线段的和不大于第三条线段,那么这三条线段就不能组成一个三角形。
三角形的三边关系
三角形的任何两边的和大于第三边。
探究交流
讨论:“任何”的含义?
利用此关系验证三条线段能否围成三角形时,只要判断较短的两条线段的和是否大于最长的线段即可。
(3)3 cm、8 cm、5 cm;
(4)4 cm、5 cm、6 cm.
(1) 15cm、10 cm、7 cm;
(2)4 cm、5 cm、10 cm;
下列长度的各组线段能否组成一个三角形?
小试牛刀
(5)a+1、a+2、a+3(a>0)
能
不能
不能
能
能
答:不能。如果此人一步能走3米,由三角形三边的关系得,此人两腿长之和要大于3米,这与实际情况相矛盾,所以他一步不能走3米。
姚明腿长1.28米
有人说他一步能走3米,你相信吗?能否用今天学过的知识去解答呢?
探究交流
探究1:已知M,N,P三点不在同一条直线上,且MN=4cm,NP=3cm,M,P两点间的距离为dcm,那么( )
A、5≤d≤7 B.1≤d≤5
C.d=5 D.1
三角形两边的长度,
第三边长度的范围你能确定吗?
两边之差<第三边<两边之和
D
探究活动
一木工有两根长分别为40厘米和60厘米的木条,要另找一根木条,钉成一个三角木架。问第三根木条的长度应在什么范围内?
20厘米<第三根木条<100厘米
探究交流
探究2:已知?ABC是等腰三角形。
(1)如果它的两条边的长分别为8cm和3cm,那么它的周长是________cm;
(2)如果它的周长是18cm,一条边的长为4cm,那么它的腰长是________cm.
19
7
检测训练
1、若下列各组值代表线段的长度,则不能构成三角形的是( )
A、3,8,4 B、4,9,6
C、15,20,8 D、9,15,8
2、现有四根木棒,长度分别为4cm,6cm,8cm,10cm,从中任取三根木棒,能组成三角形的个数为( )
A、1个 B、2个 C、3个 D、4个
A
C
检测训练
3、在△ABC中,已知a、b、c是三角形的三边,a=8cm,b=2cm,则c的取值范围是 ;
4.一个等腰三角形的两边长分别为8cm和6cm,则它的周长为______________;
5、一个等腰三角形的两边长分别为2和7,则它的周长是_______.
6cm
16
学生小结
通过这节课的学习,
你有哪些收获?
点评拓展
1、教师对本节课进行总评。
(1)三角形的三边关系
(2)判断三条线段能否组成三角形:采用一种较为简便的判法:若较短的两条边的和大于第三条边,则可构成三角形,否则不能.
(3)确定三角形第三边的取值范围:
两边之差<第三边<两边之和
(4)分类讨论等腰三角形的相关问题
2、拓展:
