华东师大版七年级下册数学课件:7.2(2) 二元一次方程组的解法(共13张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学课件:7.2(2) 二元一次方程组的解法(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 17:28:29 | ||
图片预览





文档简介
第7章 一次方程组
7.2 二元一次方程组的解法
2.加减消元法
教学目标
教学重点与难点
重点:理解并掌握加减消元法解二元一次方程组.
难点:理解解方程组的基本思想是“消元”,会化二元
一次方程组为一元一次方程.
1.使学生通过探索,逐步发现解方程的基本思想
是“消元”,化二元一次方程组为一元一次方程.
2.使学生了解“加减消元法”,并掌握加减消元法解二元一次方程组.
3.通过加减消元,使学生进一步理解把“未知”转化
为“已知”,和复杂问题转化为简单问题思想方法.
温故夯基
一. 代入消元法:
从二元一次方程组中选取一个方程,把其中的某一个
未知数用 的代数式表示出来,再代入另一个方程,达到消去一个未知数的目的,得到只含有一个未知数的 ,进而求得这个二元一次方程组的解的方法.
含另一个未知数
一元一次方程
二.代入消元法解二元一次方程组的基本步骤:
(1)从方程组中选取一个未知数系数 的方程;
(2)用一个未知数的代数式表示 未知数;
(3)把代数式代入到 ,得到一个一元一次方程;
(4)解一元一次方程,求出 的值;
(5)把未知数的值代入 ,求出另一个未知数的值;
(6)写出 .
比较简单
另一个
另一个方程
未知数
代数式
方程组的解
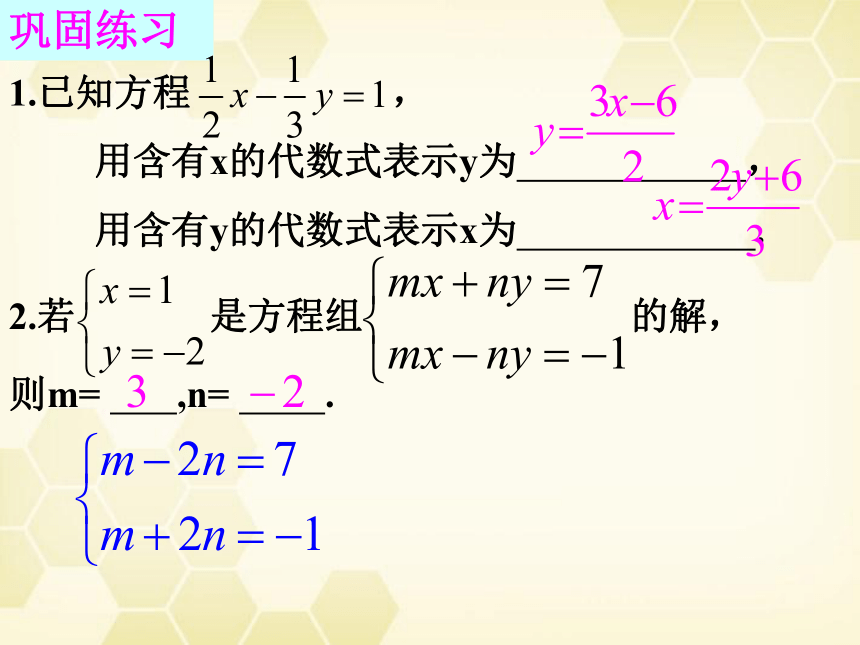
巩固练习
1.已知方程 ,
用含有x的代数式表示y为 ,
用含有y的代数式表示x为 .
2.若 是方程组 的解,
则m= ,n= .
3.若|x+y-1|+(2x-y+7)2=0,则x= ,y= .
4.若2018xa+by10与-2019xy4a+b的和是单项式,
则ba= .
学习新知
怎么解下面的二元一次方程组?
方法引入
这两个方程组中的两个方程中
未知数的系数都不是1,怎么办?
还有其他的解法吗?
方程组的各个未知数的系数有什么特点?
两个方程相加,行吗?
两个方程相减,行吗?
学习新知
一.用含有一个未知数的代数式表示另一个未知数
说明:
用含有一个未知数的代数式表示另一个未知数,
其实质就是把其中的一个未知数看成已知数的一元
一次方程.
例 (1)在方程x+y=7中,
用含有x的代数式表示y为 ,
用含有y的代数式表示x为 .
(2)在方程3x+y=17中,
用含有x的代数式表示y为 ,
用含有y的代数式表示x为 .
y=7-x
x=7-y
y=17-3x
(3)在方程3x-5y=6中,
用含有x的代数式表示y为 ,
用含有y的代数式表示x为 .
随堂练习
(2)在方程2x-7y=8中,
用含有x的代数式表示y为 ,
用含有y的代数式表示x为 .
(1)在方程3x+2y=10中,
用含有x的代数式表示y为 ,
用含有y的代数式表示x为 .
问题2
某校现有校舍20000m2,计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%.若新建校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位为m2)
如图若设应拆除旧校舍xm2,建造新校舍ym2,
请你根据题意列一个方程组.
现有校舍
20000m2
拆
除
部
分
新
建
部
分
新
建
部
分
新
建
部
分
新
建
部
分
方法引入
即:
y= 4x
y-x=6000
例1 解方程组:
①
②
解:把① 代入②,得
4x -x=6000,
3x =6000,
x =2000.
把x =2000代入①,得
y= 4×2000,
即 y=8000.
所以
y=8000.
x =2000,
思路与方法:
二元一次方程组
(其中含有用一个未知数表示另一个未知数的方程)
代入消去一个未知数
一元一次方程
代替
代入消元法
二. 代入消元法:
从二元一次方程组中选取一个方程,把其中的某一个未知数用含另一个未知数的代数式表示出来,再代入另一个方程,达到消去一个未知数的目的,得到只含有一个未知数的一元一次方程,进而求得这个二元一次方程组的解。
这种方法叫做代入消元法,简称代入法.
代入消元法解二元一次方程组的基本步骤:
(1)从方程组中选取一个未知数系数比较简单的方程;
(2)用一个未知数的代数式表示另一个未知数;
(3)把代数式代入到另一个方程,得到一个一元一次方程;
(4)解一元一次方程,求出未知数的值;
(5)把未知数的值代入代数式,求出另一个未知数的值;
(6)写出方程组的解.
例2 解方程组:
①
②
解:由①得 :
y=7-x . ③
将 ③代入 ②,得:
3x+(7-x)=17.
解得:
x=5.
将x=5代入③ ,得:
y=2.
另解:由②得 :
y=17-3x . ③
将 ③代入 ①,得:
x+(17-3x)=7.
解得:
x=5.
x=7-y . ③
3(7-y)+y=17.
y=2.
y=2
x=5.
随堂练习
解下列方程组:
①
②
解:将① 代入②,得:
(3y+2)+3y=8,
解得:
y=1.
将y=1代入①,得:
x=5.
解:将② 代入①,得:
①
②
4x-3(7-5x)=17,
解得:
x=2.
将x=2代入②,得:
y= - 3.
①
②
解:由①得:
x=y-5 . ③
将③ 代入②,得:
3(y-5)+2y=10,
解得:
y=5.
将y=5代入③,得:
x=0.
①
②
解:由②得:
y=2x-3.2 . ③
将③ 代入①,得:
2x-7(2x-3.2)=8,
解得:
x=1.2 .
将x=1.2代入③,得:
y=-0.8 .
课堂小结
1.解二元一次方程组的思想方法:通过代入的方法,
达到消元的目的,化二元一次方程组为一元一次
方程求解.
2.用代入消元法解二元一次方程组的基本步骤:
(1)从方程组中选取一个未知数系数比较简单的方程;
(2)用一个未知数的代数式表示另一个未知数;
(3)把代数式代入到另一个方程,得到一个一元一次方程;
(4)解一元一次方程,求出未知数的值;
(5)把未知数的值代入代数式,求出另一个未知数的值;
(6)写出方程组的解.
作业与课外学习任务
1.练习作业:学习检测P26-28 第1至22题
书面课本P36 习题7.2 1(1)(2)
2.课外学习任务:
预习课本P29 7.2 二元一次方程组的解法 例2
教学反馈:
作业存在的主要问题:
第7章 一次方程组
7.2 二元一次方程组的解法
2.代入消元法
教学目标
教学重点与难点
重点:理解并掌握代入消元法解未知数系数不是1的二元一次方程组.
难点:理解解方程组的基本思想是“消元”,会化二元
一次方程组为一元一次方程.
1.使学生通过探索,逐步发现解方程的基本思想
是“消元”,化二元一次方程组为一元一次方程.
2.使学生进一步理解和掌握“代入消元法”解二元
一次方程组.
3.通过代入消元,使学生进一步理解把“未知”转化
为“已知”,和复杂问题转化为简单问题思想方法.
学习新知
3.若|x+y-1|+(2x-y+7)2=0,则x= ,y= .
4.若2018xa+by10与-2019xy4a+b的和是单项式,
则ba= .
学习新知
例2 解方程组:
这两个方程组中的两个方程中
未知数的系数都不是1,怎么办?
分析
将其中一个方程适当变形,用一个未知数来表示
另一个未知数,再代入另一个方程.
①
②
解:由① 得:y=
③
将 ③代入 ②,得:
解得:
x=3.
将x=3代入③,得:
①
②
解:由① 得:x=
随堂练习
解下列方程组:
①
②
解:将① 代入②,得:
(3y+2)+3y=8,
解得:
y=1.
将y=1代入①,得:
x=5.
解:将② 代入①,得:
①
②
4x-3(7-5x)=17,
解得:
x=2.
将x=2代入②,得:
y= - 3.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
将 代入③,得:
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
将 代入③,得:
随堂练习
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
随堂练习
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
将 ③代入 ②,得:
3(3+2y)+2y=17,
随堂练习
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
将 ③代入 ②,得:
3(3+2y)+2y=17,
解得:
y=1.
将y=1代入③,得:
随堂练习
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
将 ③代入 ②,得:
3(3+2y)+2y=17,
解得:
y=1.
将y=1代入③,得:
x=5.
随堂练习
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
将 ③代入 ②,得:
3(3+2y)+2y=17,
解得:
y=1.
将y=1代入③,得:
x=5.
①
②
解:由① 得:x=3y-4. ③
随堂练习
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
将 ③代入 ②,得:
3(3+2y)+2y=17.
解得:
y=1.
将y=1代入③,得:
x=5.
①
②
解:由① 得:x=3y-4. ③
将 ③代入 ②,得:
2(3y-4)+5y=-19.
解得:
y=-1.
将y=-1代入③,得:
x=-7.
随堂练习
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
将 ③代入 ②,得:
3(3+2y)+2y=17.
解得:
y=1.
将y=1代入③,得:
x=5.
①
②
解:由① 得:x=3y-4. ③
将 ③代入 ②,得:
2(3y-4)+5y=-19.
解得:
y=-1.
将y=-1代入③,得:
x=-7.
①
②
解:由① 得:x=
①
②
解:由① 得:x=
③
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
作业与课外学习任务
1.练习作业:学习检测P26-28 第1至22题
书面课本P36 习题7.2 1(3)(4)
2.课外学习任务:
预习课本P31 7.2 二元一次方程组的解法 例3例4
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
作 业
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
将 ③代入 ②,得:
3(3+2y)+2y=17.
解得:
y=1.
将y=1代入③,得:
x=5.
①
②
解:由① 得:x=3y-4. ③
将 ③代入 ②,得:
2(3y-4)+5y=-19.
解得:
y=-1.
将y=-1代入③,得:
x=-7.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
作 业
解下列方程组:
①
②
①
②
解:由① 得:y=
③
将 ③代入 ②,得:
解得:x=2.
将x=2代入③,得:
解:由① 得:x=
③
将 ③代入 ②,得:
解得:y=-3.
将y=-3代入③,得:x=3.
第7章 一次方程组
7.2 二元一次方程组的解法
1.代入消元法
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
作 业
解下列方程组:
①
②
①
②
解:由① 得:y=
③
将 ③代入 ②,得:
解得:x=2.
将x=2代入③,得:
解:由① 得:x=
③
将 ③代入 ②,得:
解得:y=-3.
将y=-3代入③,得:x=3.
7.2 二元一次方程组的解法
2.加减消元法
教学目标
教学重点与难点
重点:理解并掌握加减消元法解二元一次方程组.
难点:理解解方程组的基本思想是“消元”,会化二元
一次方程组为一元一次方程.
1.使学生通过探索,逐步发现解方程的基本思想
是“消元”,化二元一次方程组为一元一次方程.
2.使学生了解“加减消元法”,并掌握加减消元法解二元一次方程组.
3.通过加减消元,使学生进一步理解把“未知”转化
为“已知”,和复杂问题转化为简单问题思想方法.
温故夯基
一. 代入消元法:
从二元一次方程组中选取一个方程,把其中的某一个
未知数用 的代数式表示出来,再代入另一个方程,达到消去一个未知数的目的,得到只含有一个未知数的 ,进而求得这个二元一次方程组的解的方法.
含另一个未知数
一元一次方程
二.代入消元法解二元一次方程组的基本步骤:
(1)从方程组中选取一个未知数系数 的方程;
(2)用一个未知数的代数式表示 未知数;
(3)把代数式代入到 ,得到一个一元一次方程;
(4)解一元一次方程,求出 的值;
(5)把未知数的值代入 ,求出另一个未知数的值;
(6)写出 .
比较简单
另一个
另一个方程
未知数
代数式
方程组的解
巩固练习
1.已知方程 ,
用含有x的代数式表示y为 ,
用含有y的代数式表示x为 .
2.若 是方程组 的解,
则m= ,n= .
3.若|x+y-1|+(2x-y+7)2=0,则x= ,y= .
4.若2018xa+by10与-2019xy4a+b的和是单项式,
则ba= .
学习新知
怎么解下面的二元一次方程组?
方法引入
这两个方程组中的两个方程中
未知数的系数都不是1,怎么办?
还有其他的解法吗?
方程组的各个未知数的系数有什么特点?
两个方程相加,行吗?
两个方程相减,行吗?
学习新知
一.用含有一个未知数的代数式表示另一个未知数
说明:
用含有一个未知数的代数式表示另一个未知数,
其实质就是把其中的一个未知数看成已知数的一元
一次方程.
例 (1)在方程x+y=7中,
用含有x的代数式表示y为 ,
用含有y的代数式表示x为 .
(2)在方程3x+y=17中,
用含有x的代数式表示y为 ,
用含有y的代数式表示x为 .
y=7-x
x=7-y
y=17-3x
(3)在方程3x-5y=6中,
用含有x的代数式表示y为 ,
用含有y的代数式表示x为 .
随堂练习
(2)在方程2x-7y=8中,
用含有x的代数式表示y为 ,
用含有y的代数式表示x为 .
(1)在方程3x+2y=10中,
用含有x的代数式表示y为 ,
用含有y的代数式表示x为 .
问题2
某校现有校舍20000m2,计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%.若新建校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位为m2)
如图若设应拆除旧校舍xm2,建造新校舍ym2,
请你根据题意列一个方程组.
现有校舍
20000m2
拆
除
部
分
新
建
部
分
新
建
部
分
新
建
部
分
新
建
部
分
方法引入
即:
y= 4x
y-x=6000
例1 解方程组:
①
②
解:把① 代入②,得
4x -x=6000,
3x =6000,
x =2000.
把x =2000代入①,得
y= 4×2000,
即 y=8000.
所以
y=8000.
x =2000,
思路与方法:
二元一次方程组
(其中含有用一个未知数表示另一个未知数的方程)
代入消去一个未知数
一元一次方程
代替
代入消元法
二. 代入消元法:
从二元一次方程组中选取一个方程,把其中的某一个未知数用含另一个未知数的代数式表示出来,再代入另一个方程,达到消去一个未知数的目的,得到只含有一个未知数的一元一次方程,进而求得这个二元一次方程组的解。
这种方法叫做代入消元法,简称代入法.
代入消元法解二元一次方程组的基本步骤:
(1)从方程组中选取一个未知数系数比较简单的方程;
(2)用一个未知数的代数式表示另一个未知数;
(3)把代数式代入到另一个方程,得到一个一元一次方程;
(4)解一元一次方程,求出未知数的值;
(5)把未知数的值代入代数式,求出另一个未知数的值;
(6)写出方程组的解.
例2 解方程组:
①
②
解:由①得 :
y=7-x . ③
将 ③代入 ②,得:
3x+(7-x)=17.
解得:
x=5.
将x=5代入③ ,得:
y=2.
另解:由②得 :
y=17-3x . ③
将 ③代入 ①,得:
x+(17-3x)=7.
解得:
x=5.
x=7-y . ③
3(7-y)+y=17.
y=2.
y=2
x=5.
随堂练习
解下列方程组:
①
②
解:将① 代入②,得:
(3y+2)+3y=8,
解得:
y=1.
将y=1代入①,得:
x=5.
解:将② 代入①,得:
①
②
4x-3(7-5x)=17,
解得:
x=2.
将x=2代入②,得:
y= - 3.
①
②
解:由①得:
x=y-5 . ③
将③ 代入②,得:
3(y-5)+2y=10,
解得:
y=5.
将y=5代入③,得:
x=0.
①
②
解:由②得:
y=2x-3.2 . ③
将③ 代入①,得:
2x-7(2x-3.2)=8,
解得:
x=1.2 .
将x=1.2代入③,得:
y=-0.8 .
课堂小结
1.解二元一次方程组的思想方法:通过代入的方法,
达到消元的目的,化二元一次方程组为一元一次
方程求解.
2.用代入消元法解二元一次方程组的基本步骤:
(1)从方程组中选取一个未知数系数比较简单的方程;
(2)用一个未知数的代数式表示另一个未知数;
(3)把代数式代入到另一个方程,得到一个一元一次方程;
(4)解一元一次方程,求出未知数的值;
(5)把未知数的值代入代数式,求出另一个未知数的值;
(6)写出方程组的解.
作业与课外学习任务
1.练习作业:学习检测P26-28 第1至22题
书面课本P36 习题7.2 1(1)(2)
2.课外学习任务:
预习课本P29 7.2 二元一次方程组的解法 例2
教学反馈:
作业存在的主要问题:
第7章 一次方程组
7.2 二元一次方程组的解法
2.代入消元法
教学目标
教学重点与难点
重点:理解并掌握代入消元法解未知数系数不是1的二元一次方程组.
难点:理解解方程组的基本思想是“消元”,会化二元
一次方程组为一元一次方程.
1.使学生通过探索,逐步发现解方程的基本思想
是“消元”,化二元一次方程组为一元一次方程.
2.使学生进一步理解和掌握“代入消元法”解二元
一次方程组.
3.通过代入消元,使学生进一步理解把“未知”转化
为“已知”,和复杂问题转化为简单问题思想方法.
学习新知
3.若|x+y-1|+(2x-y+7)2=0,则x= ,y= .
4.若2018xa+by10与-2019xy4a+b的和是单项式,
则ba= .
学习新知
例2 解方程组:
这两个方程组中的两个方程中
未知数的系数都不是1,怎么办?
分析
将其中一个方程适当变形,用一个未知数来表示
另一个未知数,再代入另一个方程.
①
②
解:由① 得:y=
③
将 ③代入 ②,得:
解得:
x=3.
将x=3代入③,得:
①
②
解:由① 得:x=
随堂练习
解下列方程组:
①
②
解:将① 代入②,得:
(3y+2)+3y=8,
解得:
y=1.
将y=1代入①,得:
x=5.
解:将② 代入①,得:
①
②
4x-3(7-5x)=17,
解得:
x=2.
将x=2代入②,得:
y= - 3.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
将 代入③,得:
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
将 代入③,得:
随堂练习
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
随堂练习
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
将 ③代入 ②,得:
3(3+2y)+2y=17,
随堂练习
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
将 ③代入 ②,得:
3(3+2y)+2y=17,
解得:
y=1.
将y=1代入③,得:
随堂练习
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
将 ③代入 ②,得:
3(3+2y)+2y=17,
解得:
y=1.
将y=1代入③,得:
x=5.
随堂练习
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
将 ③代入 ②,得:
3(3+2y)+2y=17,
解得:
y=1.
将y=1代入③,得:
x=5.
①
②
解:由① 得:x=3y-4. ③
随堂练习
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
将 ③代入 ②,得:
3(3+2y)+2y=17.
解得:
y=1.
将y=1代入③,得:
x=5.
①
②
解:由① 得:x=3y-4. ③
将 ③代入 ②,得:
2(3y-4)+5y=-19.
解得:
y=-1.
将y=-1代入③,得:
x=-7.
随堂练习
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
将 ③代入 ②,得:
3(3+2y)+2y=17.
解得:
y=1.
将y=1代入③,得:
x=5.
①
②
解:由① 得:x=3y-4. ③
将 ③代入 ②,得:
2(3y-4)+5y=-19.
解得:
y=-1.
将y=-1代入③,得:
x=-7.
①
②
解:由① 得:x=
①
②
解:由① 得:x=
③
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
作业与课外学习任务
1.练习作业:学习检测P26-28 第1至22题
书面课本P36 习题7.2 1(3)(4)
2.课外学习任务:
预习课本P31 7.2 二元一次方程组的解法 例3例4
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
作 业
解下列方程组:
①
②
解:由① 得:x=3+2y. ③
将 ③代入 ②,得:
3(3+2y)+2y=17.
解得:
y=1.
将y=1代入③,得:
x=5.
①
②
解:由① 得:x=3y-4. ③
将 ③代入 ②,得:
2(3y-4)+5y=-19.
解得:
y=-1.
将y=-1代入③,得:
x=-7.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
作 业
解下列方程组:
①
②
①
②
解:由① 得:y=
③
将 ③代入 ②,得:
解得:x=2.
将x=2代入③,得:
解:由① 得:x=
③
将 ③代入 ②,得:
解得:y=-3.
将y=-3代入③,得:x=3.
第7章 一次方程组
7.2 二元一次方程组的解法
1.代入消元法
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=1.
将y=1代入③,得:
x=2.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:
y=-2.
将y=-2代入③,得:
x=5.
作 业
解下列方程组:
①
②
①
②
解:由① 得:y=
③
将 ③代入 ②,得:
解得:x=2.
将x=2代入③,得:
解:由① 得:x=
③
将 ③代入 ②,得:
解得:y=-3.
将y=-3代入③,得:x=3.
