华东师大版七年级下册数学课件:7.4 实践与探索(共29张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学课件:7.4 实践与探索(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 00:00:00 | ||
图片预览







文档简介
第7章 一次方程组
7.4 实践与探索
教学目标
教学重点与难点
重点:了解并掌握列二元一次方程组解应用题的步骤.
难点:理解实际问题的题意,正确列出二元一次方程组.
1.在掌握二元一次方程组的解法后,体会二元一次
方程组与现实生活的联系及作用,经历数学建模的全过程.
2.学生初步了解列二元一次方程组解决简单的实际问题,并掌握列二元一次方程组解应用题的步骤.
列二元一次方程组解应用题的步骤:
6.检验并作答.(检验分2步:①代入方程组,②看看是否
符合题意,如不符合,则说明方程组列错了)
1.审题:仔细阅读题目,弄清题意,分清题目中的
已知量和未知量;
2.设未知数:根据题目中的问题,设两个适当的
未知数,一般设为x,y(要注意单位);
3.找等量关系:分清题目中的数量关系,找出题目中
的两个等量关系;
4.列方程组:根据等量关系列出二元一次方程组;
5.解方程组:解列出的二元一次方程组;
温故夯基
问题引入
问题1
要用20张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分做侧面,另一部分做底面.已知每张白卡纸可以做2个侧面,或者做3个底面.如果1个侧面和2个底面可以做成一个包装盒,那么如何分才能使使做成的侧面和底面正好配套?
请你设计一种分法.
白卡纸
侧面
侧面
白卡纸
底
面
底
面
底
面
1.本题有哪些已知量?
2.从已知中找出两个等量关系.
3.本题求什么?
4.若设用x张白卡纸做侧面, y张白卡纸做底面,那么可以做侧面多少个?底面多少个?
(1)共有白卡纸20张。
(2)一张白卡纸可以做2个侧面或3个底面。
(3)1个侧面与2个底面配成一套。
用几张白卡纸做侧面?几张白卡纸做底面?
(1)用做侧面的白卡纸张数+用做底面的白卡纸张数=20
(2)由已知(3)可知:侧面的个数×2=底面的个数
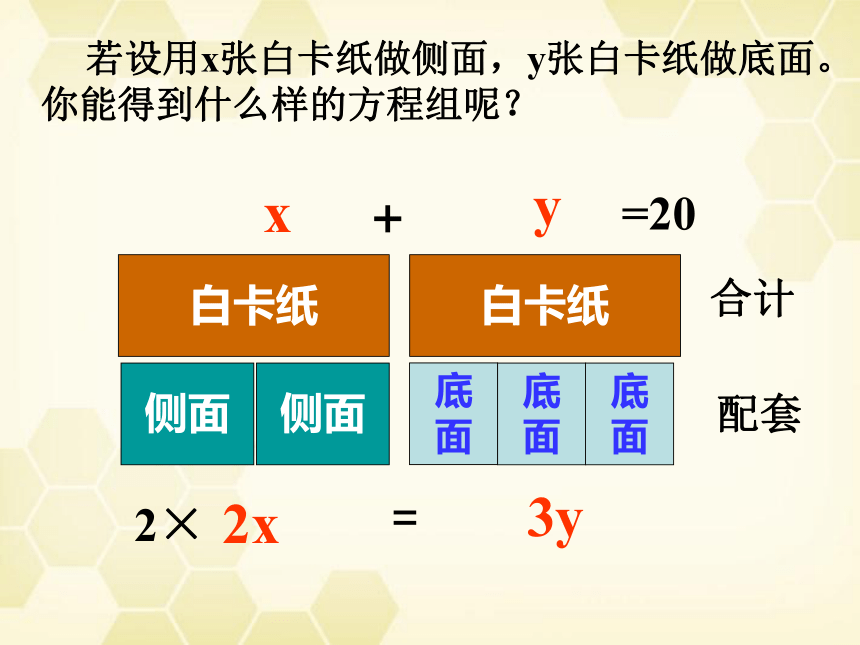
若设用x张白卡纸做侧面,y张白卡纸做底面。你能得到什么样的方程组呢?
白卡纸
侧面
底
面
侧面
底
面
底
面
2x
3y
x
y
合计
+
=20
配套
=
2×
白卡纸
解:
设用x张白卡纸做侧面,y张白卡纸做底面.
依题意得:
解方程组得:
由于解为分数,所以当白卡纸不能套裁(即一张
白卡纸只做2个侧面或3个底面)时,则最多能做
成 个包装盒.
16
若可以套裁呢?
最多可以做几个?
怎么做?
当白卡纸可以套裁时,用8张做侧面,11张做底面,
另一张套裁出1个侧面,1个底面,则共可做盒身17个,
盒底盖34个,正好配成17个包装盒,充分利用了材料.
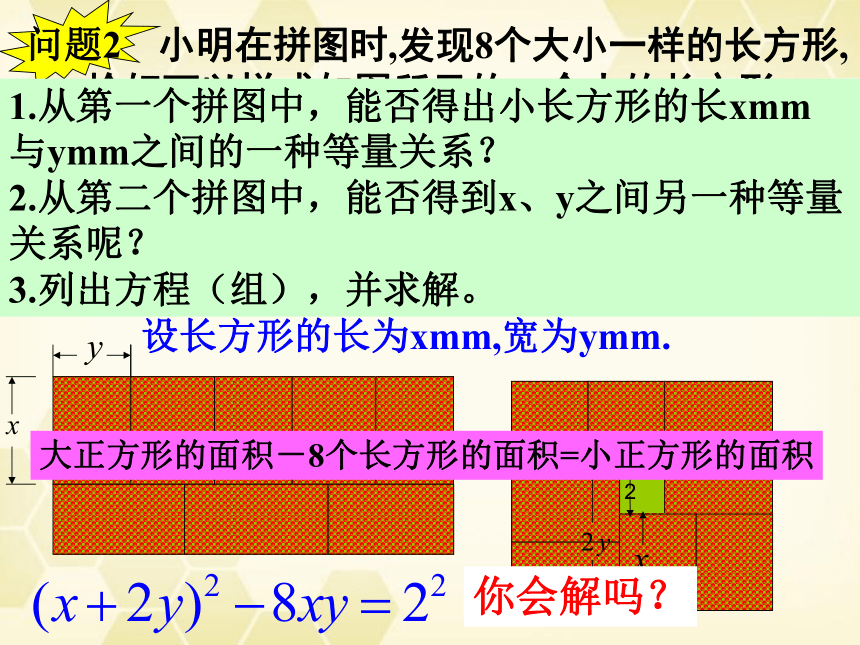
小明在拼图时,发现8个大小一样的长方形,
恰好可以拼成如图所示的一个大的长方形.
小红看见了,说:“我来试一试.”结果小红七拼八凑,拼成如图所示的正方形.咳,怎么中间还留下了一个洞,恰好是边长为2mm的小正方形!
2
你能求出这些长方形的长和宽吗?
问题2
设长方形的长为xmm,宽为ymm.
1.从第一个拼图中,能否得出小长方形的长xmm
与ymm之间的一种等量关系? 2.从第二个拼图中,能否得到x、y之间另一种等量关系呢?
3.列出方程(组),并求解。
大正方形的面积-8个长方形的面积=小正方形的面积
你会解吗?
2
设长方形的长为xmm,宽为ymm.
1.从第一个拼图中,能否得出小长方形的长xmm
与ymm之间的一种等量关系?
2.从第二个拼图中,能否得到x、y之间另一种等量关系呢?
3.列出方程(组),并求解.
3x=5y
2y=x+2
随堂练习
1.某市为更有效地利用水资源,制定了用水标准:如果一户三口之家每月用水量不超过Am3 ,按每立方米水1.30元收费;如果超过Am3 ,超过部分按每立方米水2.90元收费,其余仍按每立方米水1.30元收费.小红一家三人,1月份共用水12 m3 ,支付水费22元.问该市制定的用水标准A为多少?小红一家超过部分的用水是多少立方米?
解:设该市制定的用水标准A为x m3,
小红一家超过部分的用水ym3 ,
依题意得:
解得:
答:该市制定的用水标准A为8 m3,
小红一家超过部分的用水4m3 .
经检验,符合题意.
2.长风乐园的门票价格如下表所列.某校七年级(1)、(2)两个班共104人去游长风乐园,其中(1)班人数较少,不到50人,
(2)班人数较多,有50多人.经估算,如果两个班都以班为单位分别购票,那么一共应付1240元;如果两个班联合起来,作为一个团体购票,那么可以节省不少钱.问两个班各有多少名学生?
购票人数(人)
1~50人
51~100人
100人以上
每人门票价(人)
13元
11元
9元
解:设七年级(1)班有x 名学生,七年级(2)班有y名学生,
依题意得:
解得:
答:七年级(1)班有48 名学生,七年级(2)班有56名学生.
经检验,符合题意.
例题精析
例1 今年,小李的年龄是他爷爷的 .小李发现,12年之后,
他的年龄变成爷爷的 .试求出今年小李的年龄.
解:设小李今年的年龄为x岁,
爷爷的年龄为y岁,
小李的年龄 爷爷的年龄
今年
12年后
依题意得:
解得:
经检验,符合题意.
答:小李今年的年龄为12岁.
随堂练习
1.小明与他的爸爸一起做“投篮球〞游戏.两人商定
规则为:小明投中1个得3分,小明爸爸投中1个得1分
.结果两人一共投中了20个,经计算,发现两人的得分恰好相等.你能知道他们两人各投中几个吗?
解:小明投中x个,他爸爸投中y个,
依题意得:
解得:
经检验,符合题意.
答:小明投中5个,他爸爸投中15个.
2.某检测站计划在规定时间内检测一批仪器,如果每天检测30台,那么在规定时间内只能完成检测
计划数的 .现在每天实际检测40台,结果不但比原
计划提前了一天完成任务,还多检测了25台.
问规定时间是多少天?原计划检测多少台?
解:设规定时间是x天,原计划检测仪器y台,
依题意得:
解得:
答:规定时间是25天,原计划检测仪器975台.
经检验,符合题意.
例题精析
例2 A、B两地相距3千米.甲从A地出发步行到B地,
乙从B地出发步行到A地.两人同时出发,20分钟后
相遇,又经过10分钟后,甲所余路程为乙所余路程的
2倍,求两人的速度.
解:设甲,乙两人的速度分别为x千米/时,y千米/时,
依题意得:
解得:
答:甲,乙两人的速度分别为4千米/时,5千米/时.
经检验,符合题意.
随堂练习
1.甲、乙两人同时加工一批零件,前3小时两人共
加工126件,后5小时中甲先花了1小时修理工具,
之后甲每小时比以前多加工10件,结果在后5小时
内,甲比乙多加工了10件.甲、乙两人原来每小时
各加工多少件?
解:设甲、乙两人原来每小时分别加工x件、y件,
依题意得:
解得:
经检验,符合题意.
答:甲、乙两人原来每小时分别加工20件、22件.
2.已知某个三角形的周长为18cm,其中两条边的
长度之和等于第三条边长度的2倍,而它们的差等于
第三条边长度的1/3,求这个三角形三边的长度.
解:设这个三角形的两边长分别为 x cm, y cm,
则第三条边为 cm,
(18 –x-y)
依题意得:
解得:
∴第三条边:18 – x - y=
18 -7-5 = 6.
经检验,符合题意.
答:这个三角形的三边长分别为 7 cm, 5 cm, 6cm.
2.已知某个三角形的周长为18cm,其中两条边的
长度之和等于第三条边长度的2倍,而它们的差等于
第三条边长度的1/3,求这个三角形三边的长度.
解:设这个三角形的三边长分别为 xcm, ycm, zcm,
依题意得:
解得:
经检验,符合题意.
答:这个三角形的三边长分别为 7 cm, 5 cm, 6cm.
例题精析
例3 两块试验田去年共产花生470千克.改用良种后,今年共产花生523千克.已知第一块田的产量比去年增产16%,第二块田的产量比去年增产10%.求改用良种后每块田的产量.
解:设改用良种后第一块田和第二块田的产量
分别为x千克和y千克,
依题意得:
即:
①
②
由① 得:y=523-x.
③
将 ③代入 ②,得:
∴ 1.1x+1.16(523-x)=1.16×1.1×470,
∴ 1.1x+606.68-1.16x=599.72,
∴ 1.1x-1.16x=599.72 -606.68,
∴ -0.06x= -6.96,
∴ x= 116.
将x=116代入③,得:
y=407.
例题精析
例3 两块试验田去年共产花生470千克.改用良种后,今年共产花生523千克.已知第一块田的产量比去年增产16%,第二块田的产量比去年增产10%.求改用良种后每块田的产量.
解:设改用良种后第一块田和第二块田的产量
分别为x千克和y千克,
依题意得:
即:
解得:
经检验,符合题意.
答:改用良种后第一块田和第二块田的产量分别为116千克 和407千克.
有没有其他假设方法呢?
例题精析
例3 两块试验田去年共产花生470千克.改用良种后,今年共产花生523千克.已知第一块田的产量比去年增产16%,第二块田的产量比去年增产10%.求改用良种后每块田的产量.
解:设去年第一块田和第二块田的产量分别为x千克
和y千克,
依题意得:
即:
解得:
经检验,符合题意.
答:改用良种后第一块田和第二块田的产量分别为116千克 和407千克.
∴ (1+16%)x=116, (1+10%)y=407.
随堂练习
1.二果问价(源于我国古代算书《四元玉鉴》):
九百九十九文钱 甜果苦果买一千
甜果九个十一文 苦果七个四文钱
试问甜苦果几个 又问各该几个钱
解:设购买甜果和苦果分别为x个,y个,
依题意得:
解得:
经检验,符合题意.
答:购买甜果657个,用了803文钱;
购买苦果343个,用了196文钱.
2.一张方桌由1个桌面、4条桌腿组成.如果1立方米
木料可以做方桌的桌面50个或做桌腿300条,现有5
立方米木料,那么用多少立方米木料做桌面、多少
立方米做桌腿,做出的桌面和桌腿能恰好配成方桌?
能配成多少张方桌?
解:设用x立方米木料做桌面,用y立方米木料做桌腿,
依题意得:
解得:
经检验,符合题意.
答:用3立方米木料做桌面,用2立方米木料做桌腿,
恰好能配成方桌,能配成150张方桌.
例4 客车和货车分别在两条平行的铁轨上行驶,
客车长450米,货车长600米.如果两车相向而行,那么从两车车头相遇到车尾离开共需21秒钟;如果客车从后面追货车,那么从客车车头到客车车尾离开货车车头共需1分45秒.求两车的速度.
例题精析
解:设客车和货车的速度分别为x米/秒,y米/秒,
依题意得:
解得:
30米/秒=108千米/时,
20米/秒=72千米/时.
答:客车和货车的速度分别为108千米/时和72千米/时.
经检验,符合题意.
随堂练习
李老师去一家文具店给美术小组的30名同学买铅笔和橡皮.
到了商店后发现,按商店规定,如果给全组每人都买2枝铅笔
和1块橡皮,那么按零售价计算,共需付30元;如果给全组每人都买3枝铅笔和2块橡皮,那么可以按批发价计算,共需要付40.50元.已知每支铅笔的批发价比零售价低0.05元,每块橡皮的批发价比零售价低0.10元.这家文具店每枝铅笔和
每块橡皮的批发价各是多少元?
解:设每枝铅笔和每块橡皮的批发价分别是x元,y元,
依题意得:
解得:
经检验,符合题意.
答:每枝铅笔和每块橡皮的批发价分别是0.25元和0.30元.
列二元一次方程组解应用题的步骤:
课堂小结
6.检验并作答.(检验分2步:①代入方程组,②看看是否
符合题意,如不符合,则说明方程组列错了)
1.审题:仔细阅读题目,弄清题意,分清题目中的
已知量和未知量;
2.设未知数:根据题目中的问题,设两个适当的
未知数,一般设为x,y(要注意单位);
3.找等量关系:分清题目中的数量关系,找出题目中
的两个等量关系;
4.列方程组:根据等量关系列出二元一次方程组;
5.解方程组:解列出的二元一次方程组;
作业与课外学习任务
1.练习作业:学习检测P37-40 第1至19题
2.课外学习任务:
预习课本P50 8.1 认识不等式
教学反馈:
作业存在的主要问题:
7.4 实践与探索
教学目标
教学重点与难点
重点:了解并掌握列二元一次方程组解应用题的步骤.
难点:理解实际问题的题意,正确列出二元一次方程组.
1.在掌握二元一次方程组的解法后,体会二元一次
方程组与现实生活的联系及作用,经历数学建模的全过程.
2.学生初步了解列二元一次方程组解决简单的实际问题,并掌握列二元一次方程组解应用题的步骤.
列二元一次方程组解应用题的步骤:
6.检验并作答.(检验分2步:①代入方程组,②看看是否
符合题意,如不符合,则说明方程组列错了)
1.审题:仔细阅读题目,弄清题意,分清题目中的
已知量和未知量;
2.设未知数:根据题目中的问题,设两个适当的
未知数,一般设为x,y(要注意单位);
3.找等量关系:分清题目中的数量关系,找出题目中
的两个等量关系;
4.列方程组:根据等量关系列出二元一次方程组;
5.解方程组:解列出的二元一次方程组;
温故夯基
问题引入
问题1
要用20张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分做侧面,另一部分做底面.已知每张白卡纸可以做2个侧面,或者做3个底面.如果1个侧面和2个底面可以做成一个包装盒,那么如何分才能使使做成的侧面和底面正好配套?
请你设计一种分法.
白卡纸
侧面
侧面
白卡纸
底
面
底
面
底
面
1.本题有哪些已知量?
2.从已知中找出两个等量关系.
3.本题求什么?
4.若设用x张白卡纸做侧面, y张白卡纸做底面,那么可以做侧面多少个?底面多少个?
(1)共有白卡纸20张。
(2)一张白卡纸可以做2个侧面或3个底面。
(3)1个侧面与2个底面配成一套。
用几张白卡纸做侧面?几张白卡纸做底面?
(1)用做侧面的白卡纸张数+用做底面的白卡纸张数=20
(2)由已知(3)可知:侧面的个数×2=底面的个数
若设用x张白卡纸做侧面,y张白卡纸做底面。你能得到什么样的方程组呢?
白卡纸
侧面
底
面
侧面
底
面
底
面
2x
3y
x
y
合计
+
=20
配套
=
2×
白卡纸
解:
设用x张白卡纸做侧面,y张白卡纸做底面.
依题意得:
解方程组得:
由于解为分数,所以当白卡纸不能套裁(即一张
白卡纸只做2个侧面或3个底面)时,则最多能做
成 个包装盒.
16
若可以套裁呢?
最多可以做几个?
怎么做?
当白卡纸可以套裁时,用8张做侧面,11张做底面,
另一张套裁出1个侧面,1个底面,则共可做盒身17个,
盒底盖34个,正好配成17个包装盒,充分利用了材料.
小明在拼图时,发现8个大小一样的长方形,
恰好可以拼成如图所示的一个大的长方形.
小红看见了,说:“我来试一试.”结果小红七拼八凑,拼成如图所示的正方形.咳,怎么中间还留下了一个洞,恰好是边长为2mm的小正方形!
2
你能求出这些长方形的长和宽吗?
问题2
设长方形的长为xmm,宽为ymm.
1.从第一个拼图中,能否得出小长方形的长xmm
与ymm之间的一种等量关系? 2.从第二个拼图中,能否得到x、y之间另一种等量关系呢?
3.列出方程(组),并求解。
大正方形的面积-8个长方形的面积=小正方形的面积
你会解吗?
2
设长方形的长为xmm,宽为ymm.
1.从第一个拼图中,能否得出小长方形的长xmm
与ymm之间的一种等量关系?
2.从第二个拼图中,能否得到x、y之间另一种等量关系呢?
3.列出方程(组),并求解.
3x=5y
2y=x+2
随堂练习
1.某市为更有效地利用水资源,制定了用水标准:如果一户三口之家每月用水量不超过Am3 ,按每立方米水1.30元收费;如果超过Am3 ,超过部分按每立方米水2.90元收费,其余仍按每立方米水1.30元收费.小红一家三人,1月份共用水12 m3 ,支付水费22元.问该市制定的用水标准A为多少?小红一家超过部分的用水是多少立方米?
解:设该市制定的用水标准A为x m3,
小红一家超过部分的用水ym3 ,
依题意得:
解得:
答:该市制定的用水标准A为8 m3,
小红一家超过部分的用水4m3 .
经检验,符合题意.
2.长风乐园的门票价格如下表所列.某校七年级(1)、(2)两个班共104人去游长风乐园,其中(1)班人数较少,不到50人,
(2)班人数较多,有50多人.经估算,如果两个班都以班为单位分别购票,那么一共应付1240元;如果两个班联合起来,作为一个团体购票,那么可以节省不少钱.问两个班各有多少名学生?
购票人数(人)
1~50人
51~100人
100人以上
每人门票价(人)
13元
11元
9元
解:设七年级(1)班有x 名学生,七年级(2)班有y名学生,
依题意得:
解得:
答:七年级(1)班有48 名学生,七年级(2)班有56名学生.
经检验,符合题意.
例题精析
例1 今年,小李的年龄是他爷爷的 .小李发现,12年之后,
他的年龄变成爷爷的 .试求出今年小李的年龄.
解:设小李今年的年龄为x岁,
爷爷的年龄为y岁,
小李的年龄 爷爷的年龄
今年
12年后
依题意得:
解得:
经检验,符合题意.
答:小李今年的年龄为12岁.
随堂练习
1.小明与他的爸爸一起做“投篮球〞游戏.两人商定
规则为:小明投中1个得3分,小明爸爸投中1个得1分
.结果两人一共投中了20个,经计算,发现两人的得分恰好相等.你能知道他们两人各投中几个吗?
解:小明投中x个,他爸爸投中y个,
依题意得:
解得:
经检验,符合题意.
答:小明投中5个,他爸爸投中15个.
2.某检测站计划在规定时间内检测一批仪器,如果每天检测30台,那么在规定时间内只能完成检测
计划数的 .现在每天实际检测40台,结果不但比原
计划提前了一天完成任务,还多检测了25台.
问规定时间是多少天?原计划检测多少台?
解:设规定时间是x天,原计划检测仪器y台,
依题意得:
解得:
答:规定时间是25天,原计划检测仪器975台.
经检验,符合题意.
例题精析
例2 A、B两地相距3千米.甲从A地出发步行到B地,
乙从B地出发步行到A地.两人同时出发,20分钟后
相遇,又经过10分钟后,甲所余路程为乙所余路程的
2倍,求两人的速度.
解:设甲,乙两人的速度分别为x千米/时,y千米/时,
依题意得:
解得:
答:甲,乙两人的速度分别为4千米/时,5千米/时.
经检验,符合题意.
随堂练习
1.甲、乙两人同时加工一批零件,前3小时两人共
加工126件,后5小时中甲先花了1小时修理工具,
之后甲每小时比以前多加工10件,结果在后5小时
内,甲比乙多加工了10件.甲、乙两人原来每小时
各加工多少件?
解:设甲、乙两人原来每小时分别加工x件、y件,
依题意得:
解得:
经检验,符合题意.
答:甲、乙两人原来每小时分别加工20件、22件.
2.已知某个三角形的周长为18cm,其中两条边的
长度之和等于第三条边长度的2倍,而它们的差等于
第三条边长度的1/3,求这个三角形三边的长度.
解:设这个三角形的两边长分别为 x cm, y cm,
则第三条边为 cm,
(18 –x-y)
依题意得:
解得:
∴第三条边:18 – x - y=
18 -7-5 = 6.
经检验,符合题意.
答:这个三角形的三边长分别为 7 cm, 5 cm, 6cm.
2.已知某个三角形的周长为18cm,其中两条边的
长度之和等于第三条边长度的2倍,而它们的差等于
第三条边长度的1/3,求这个三角形三边的长度.
解:设这个三角形的三边长分别为 xcm, ycm, zcm,
依题意得:
解得:
经检验,符合题意.
答:这个三角形的三边长分别为 7 cm, 5 cm, 6cm.
例题精析
例3 两块试验田去年共产花生470千克.改用良种后,今年共产花生523千克.已知第一块田的产量比去年增产16%,第二块田的产量比去年增产10%.求改用良种后每块田的产量.
解:设改用良种后第一块田和第二块田的产量
分别为x千克和y千克,
依题意得:
即:
①
②
由① 得:y=523-x.
③
将 ③代入 ②,得:
∴ 1.1x+1.16(523-x)=1.16×1.1×470,
∴ 1.1x+606.68-1.16x=599.72,
∴ 1.1x-1.16x=599.72 -606.68,
∴ -0.06x= -6.96,
∴ x= 116.
将x=116代入③,得:
y=407.
例题精析
例3 两块试验田去年共产花生470千克.改用良种后,今年共产花生523千克.已知第一块田的产量比去年增产16%,第二块田的产量比去年增产10%.求改用良种后每块田的产量.
解:设改用良种后第一块田和第二块田的产量
分别为x千克和y千克,
依题意得:
即:
解得:
经检验,符合题意.
答:改用良种后第一块田和第二块田的产量分别为116千克 和407千克.
有没有其他假设方法呢?
例题精析
例3 两块试验田去年共产花生470千克.改用良种后,今年共产花生523千克.已知第一块田的产量比去年增产16%,第二块田的产量比去年增产10%.求改用良种后每块田的产量.
解:设去年第一块田和第二块田的产量分别为x千克
和y千克,
依题意得:
即:
解得:
经检验,符合题意.
答:改用良种后第一块田和第二块田的产量分别为116千克 和407千克.
∴ (1+16%)x=116, (1+10%)y=407.
随堂练习
1.二果问价(源于我国古代算书《四元玉鉴》):
九百九十九文钱 甜果苦果买一千
甜果九个十一文 苦果七个四文钱
试问甜苦果几个 又问各该几个钱
解:设购买甜果和苦果分别为x个,y个,
依题意得:
解得:
经检验,符合题意.
答:购买甜果657个,用了803文钱;
购买苦果343个,用了196文钱.
2.一张方桌由1个桌面、4条桌腿组成.如果1立方米
木料可以做方桌的桌面50个或做桌腿300条,现有5
立方米木料,那么用多少立方米木料做桌面、多少
立方米做桌腿,做出的桌面和桌腿能恰好配成方桌?
能配成多少张方桌?
解:设用x立方米木料做桌面,用y立方米木料做桌腿,
依题意得:
解得:
经检验,符合题意.
答:用3立方米木料做桌面,用2立方米木料做桌腿,
恰好能配成方桌,能配成150张方桌.
例4 客车和货车分别在两条平行的铁轨上行驶,
客车长450米,货车长600米.如果两车相向而行,那么从两车车头相遇到车尾离开共需21秒钟;如果客车从后面追货车,那么从客车车头到客车车尾离开货车车头共需1分45秒.求两车的速度.
例题精析
解:设客车和货车的速度分别为x米/秒,y米/秒,
依题意得:
解得:
30米/秒=108千米/时,
20米/秒=72千米/时.
答:客车和货车的速度分别为108千米/时和72千米/时.
经检验,符合题意.
随堂练习
李老师去一家文具店给美术小组的30名同学买铅笔和橡皮.
到了商店后发现,按商店规定,如果给全组每人都买2枝铅笔
和1块橡皮,那么按零售价计算,共需付30元;如果给全组每人都买3枝铅笔和2块橡皮,那么可以按批发价计算,共需要付40.50元.已知每支铅笔的批发价比零售价低0.05元,每块橡皮的批发价比零售价低0.10元.这家文具店每枝铅笔和
每块橡皮的批发价各是多少元?
解:设每枝铅笔和每块橡皮的批发价分别是x元,y元,
依题意得:
解得:
经检验,符合题意.
答:每枝铅笔和每块橡皮的批发价分别是0.25元和0.30元.
列二元一次方程组解应用题的步骤:
课堂小结
6.检验并作答.(检验分2步:①代入方程组,②看看是否
符合题意,如不符合,则说明方程组列错了)
1.审题:仔细阅读题目,弄清题意,分清题目中的
已知量和未知量;
2.设未知数:根据题目中的问题,设两个适当的
未知数,一般设为x,y(要注意单位);
3.找等量关系:分清题目中的数量关系,找出题目中
的两个等量关系;
4.列方程组:根据等量关系列出二元一次方程组;
5.解方程组:解列出的二元一次方程组;
作业与课外学习任务
1.练习作业:学习检测P37-40 第1至19题
2.课外学习任务:
预习课本P50 8.1 认识不等式
教学反馈:
作业存在的主要问题:
