华东师大版七年级下册数学课件:8.2.2 不等式的简单变形(共19张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学课件:8.2.2 不等式的简单变形(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
第8章 一元一次不等式
8.2 解一元一次不等式
2. 不等式的简单变形
教学目标
教学重点与难点
重点:不等式的性质1,2,3,并能利用它们对不等式进行简单变形.
难点:理解不等式的性质1,2,3.
1.让学生理解和掌握不等式的性质.
2. 会利用不等式的性质对不等式进行简单变形.
温故夯基
一.不等式的解集:
一个不等式的所有解组成的集合。
不等式的解集必须满足两个条件:
(1)解集中的任何一个数值都使不等式成立;
(2)解集外的任何一个数值都不能使不等式成立.
二.解不等式:
求不等式的解集的过程,叫做解不等式。
三.在数轴上表示不等式的解集的方法:
(1)画数轴;
(2)定边界点;
(3)定方向.
包含用实心点表示;
不包含用空心点表示。
大于向右画,小于向左画。
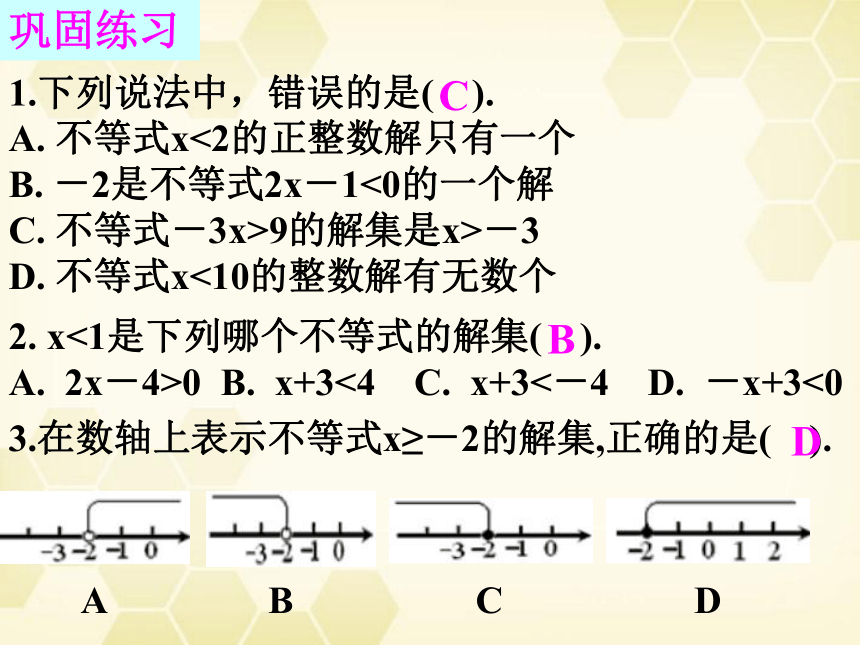
巩固练习
1.下列说法中,错误的是( ).
A. 不等式x<2的正整数解只有一个
B. -2是不等式2x-1<0的一个解
C. 不等式-3x>9的解集是x>-3
D. 不等式x<10的整数解有无数个
C
2. x<1是下列哪个不等式的解集( ).
A. 2x-4>0 B. x+3<4 C. x+3<-4 D. -x+3<0
B
3.在数轴上表示不等式x≥-2的解集,正确的是( ).
A B C D
D
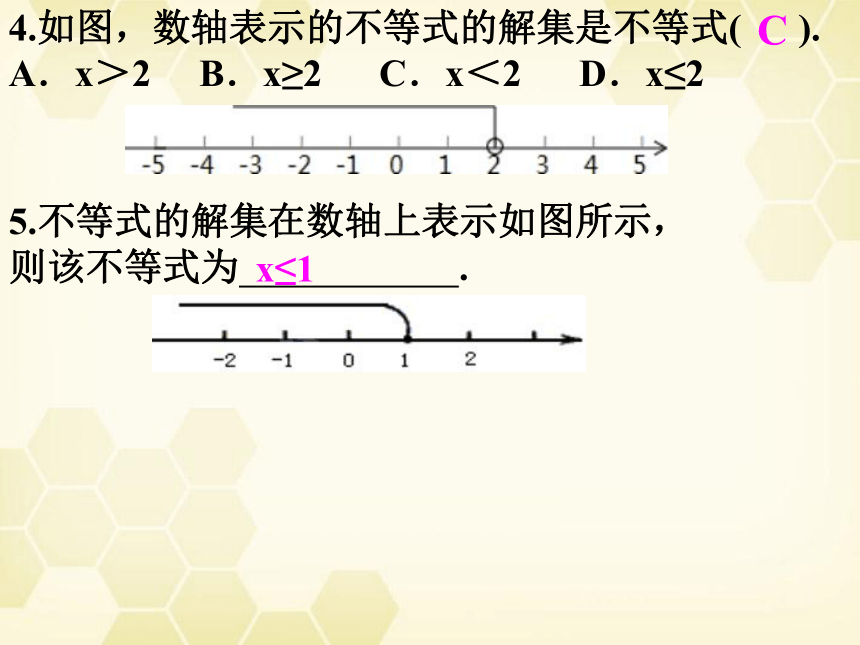
4.如图,数轴表示的不等式的解集是不等式( ).
A.x>2 B.x≥2 C.x<2 D.x≤2
C
5.不等式的解集在数轴上表示如图所示,
则该不等式为 .
x≤1
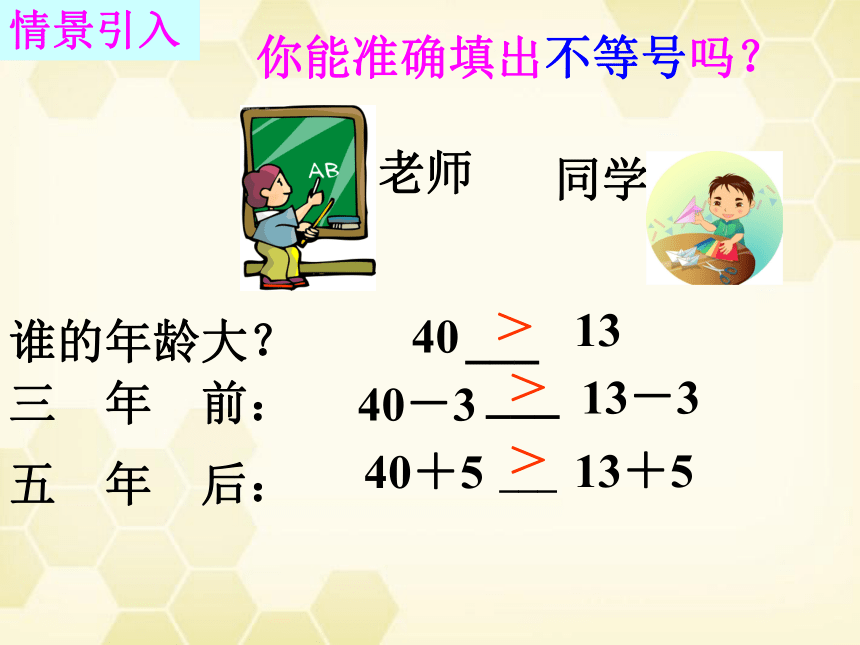
你能准确填出不等号吗?
老师
谁的年龄大?
40
13
三 年 前:
五 年 后:
40-3
13-3
40+5
13+5
>
>
>
___
___
___
同学
情景引入
某老师今年a岁,某同学今年b岁,
如果老师与学生的年龄大小关系是:
c年前则有:
a__b
>
c年后则有:
a+c
b+c
__
>
a-c
b-c
__
>
结论:
不等式的性质1
如果a>b,那么a+c > b+c, a-c >b-c.
即:不等式的两边都加上(或都减去)同一个数或
同一个整式,不等号的方向不变。
根据上面的结论,请你试一试?
1.如果x>y,那么x+5 __ y+5,x-7__ y-7.
>
2.如果3x<-2,那么3x+m___-2+m,
3x-2x___-2-2x.
3.如果a+10<b+10, 那么a___b,为什么?
4.如果a-4>b-4, 那么a___b,为什么?
<
>
<
<
>
如果a>b,那么a+c > b+c, a-c >b-c.
<
>
>
>
<
<
=
不等式的两边都乘以(或都除以)同一个不为零的数,不等号的方向是否改变呢?
将不等式 7>4 的两边都乘以同一个数,
比较所得结果的大小,用 >、< 、= 填空:
7×3 4×3, 7×(-1) 4 × (-1),
7×2 4×2, 7 ×(-2) 4 × (-2),
7×1 4×1, 7 × (-3) 4 × (-3),
7×0 4×0,
思考
试一试
你能从中发现什么?
同乘以一个正数,不等号方向不变,
同乘以一个负数不等号方向改变,
同乘以0的时候相等.
结论:
不等式的性质2
如果a>b,并且c >0,那么ac > bc, .
不等式的性质3
如果a>b,并且c <0,那么ac < bc, .
也就是说,不等式的两边都____________ 同一个
正数,不等号的方向_______;
不等式的两边都_____________同一个
负数,不等号的方向________.
乘以(或除以)
不变
乘以(或除以)
改变
比较等式的性质和不等式的性质的异同
等式两边都加上或减去同一个数或整式,所得
结果仍是等式.
等式两边都乘以或除以同一个不等于零的数,所得结果仍是等式
不等式的两边都加上(或减去)同一个数或同一个
整式,不等号方向不变.
不等式的两边都乘以或除以同一正数,不等号方向不变.
不等式的两边都乘以或除以同一负数,不等号方向改变.
解:方程的两边都加上7,等式仍然成立,所以
与解方程一样,解不等式的过程,就是要将不等式变形成x>a 或x例 解方程: x -7=8
解不等式:x -7<8
x-7+7=8+7,
解:不等式的两边都
加上7,不等号的方向
不变,所以
x-7+7 8+7,
x< 8+7,
<
x=8+7,
x=15.
x< 15.
例题精析
例1 解不等式:
(1) x+7>8; (2) 3x<2x-7.
解:(1)不等式的两边都减去7,不等号的方向不变,
∴ x+7 -7 >8 -7,
∴ x>1.
(2)不等式的两边都减去2x,不等号的方向不变,
∴ 3x -2x <2x-7 -2x,
∴ x <-7 .
这两小题中不等式的变形
与方程的什么变形类似?
移项
将不等式的某些项改变符号后移到不等式的
另一边,不等式的方向不变.
解下列不等式:
(1) x-2<3 ; (2) x+1≥7;
(3) 4+5x≤4x; (4) 7x+15>6x+13.
随堂练习
解:(1)不等式的两边都加上2,不等号的方向不变,
∴ x -2+2 <3+2,
∴ x <5.
(2)不等式的两边都减去1,不等号的方向不变,
∴ x+1 -1≥7 -1,
∴ x≥6.
(3)不等式的两边都加上(-4x-4),不等号的方向不变,
∴ 4+5x -4x-4 ≤4x -4x-4,
∴ x≤-4.
(4)不等式的两边都加上(-6x-15),不等号的方向不变,
∴ 7x+15 -6x-15 >6x+13 -6x-15,
∴ x >-2.
例题精析
例2 解不等式:
(1) ; (2) -2x<6.
解:(1)不等式的两边都乘以2,不等号的方向不变,
∴ x> - 6.
(2)不等式的两边都除以-2,不等号的方向改变,
∴ (-2x)÷ (-2) > 6 ÷(-2),
∴ x >-3 .
系数化为1
这两小题中不等式的变形
与方程的什么变形类似?
有什么不同?
要注意系数的正负!
正不变,负改变.
解下列不等式,并将解集在数轴上表示出来:
-2x>4; (2) 3x≤0;
(3) 5x>20; (4) -4x≥-12.
随堂练习
(1)不等式的两边都除以-2,不等号的方向改变,
∴ (-2x)÷ (-2) < 4 ÷(-2),
∴ x < -2.
(2)不等式的两边都除以3,不等号的方向不变,
∴ 3x÷ 3 ≤ 0÷3,
∴ x≤ 0 .
(3)不等式的两边都除以5,不等号的方向不变,
∴ 5x÷ 5> 20 ÷5,
∴ x> 4.
(4)不等式的两边都除以-4,不等号的方向改变,
∴ (-4x)÷ (-4) ≤ (-12) ÷(-4),
∴ x≤ 3 .
一.不等式的性质
课堂小结
性质1
如果a>b,那么a+c > b+c, a-c >b-c.
性质2
性质3
如果a>b,并且c >0,那么ac > bc, .
如果a>b,并且c <0,那么ac < bc, .
二. 解一元一次不等式的过程,类似于解一元一次
方程,就是将不等式进行一系列的变形,最终转化
成x >a( x≥a)或x作业与课外学习任务
1.练习作业:学习检测P45-46 第1至21题
书面课本P61 习题8.2 1
2.课外学习任务:
预习课本P58 8.2.3 解一元一次不等式
教学反馈:
作业存在的主要问题:
第8章 一元一次不等式
8.2 解一元一次不等式
2. 不等式的简单变形
教学目标
教学重点与难点
重点:不等式的性质1,2,3,并能利用它们对不等式进行简单变形.
难点:理解不等式的性质1,2,3.
1.让学生理解和掌握不等式的性质.
2. 会利用不等式的性质对不等式进行简单变形.
温故夯基
一.不等式的解集:
一个不等式的所有解组成的集合。
不等式的解集必须满足两个条件:
(1)解集中的任何一个数值都使不等式成立;
(2)解集外的任何一个数值都不能使不等式成立.
二.解不等式:
求不等式的解集的过程,叫做解不等式。
三.在数轴上表示不等式的解集的方法:
(1)画数轴;
(2)定边界点;
(3)定方向.
包含用实心点表示;
不包含用空心点表示。
大于向右画,小于向左画。
巩固练习
1.下列说法中,错误的是( ).
A. 不等式x<2的正整数解只有一个
B. -2是不等式2x-1<0的一个解
C. 不等式-3x>9的解集是x>-3
D. 不等式x<10的整数解有无数个
C
2. x<1是下列哪个不等式的解集( ).
A. 2x-4>0 B. x+3<4 C. x+3<-4 D. -x+3<0
B
3.在数轴上表示不等式x≥-2的解集,正确的是( ).
A B C D
D
4.如图,数轴表示的不等式的解集是不等式( ).
A.x>2 B.x≥2 C.x<2 D.x≤2
C
5.不等式的解集在数轴上表示如图所示,
则该不等式为 .
x≤1
你能准确填出不等号吗?
老师
谁的年龄大?
40
13
三 年 前:
五 年 后:
40-3
13-3
40+5
13+5
>
>
>
___
___
___
同学
情景引入
某老师今年a岁,某同学今年b岁,
如果老师与学生的年龄大小关系是:
c年前则有:
a__b
>
c年后则有:
a+c
b+c
__
>
a-c
b-c
__
>
结论:
不等式的性质1
如果a>b,那么a+c > b+c, a-c >b-c.
即:不等式的两边都加上(或都减去)同一个数或
同一个整式,不等号的方向不变。
根据上面的结论,请你试一试?
1.如果x>y,那么x+5 __ y+5,x-7__ y-7.
>
2.如果3x<-2,那么3x+m___-2+m,
3x-2x___-2-2x.
3.如果a+10<b+10, 那么a___b,为什么?
4.如果a-4>b-4, 那么a___b,为什么?
<
>
<
<
>
如果a>b,那么a+c > b+c, a-c >b-c.
<
>
>
>
<
<
=
不等式的两边都乘以(或都除以)同一个不为零的数,不等号的方向是否改变呢?
将不等式 7>4 的两边都乘以同一个数,
比较所得结果的大小,用 >、< 、= 填空:
7×3 4×3, 7×(-1) 4 × (-1),
7×2 4×2, 7 ×(-2) 4 × (-2),
7×1 4×1, 7 × (-3) 4 × (-3),
7×0 4×0,
思考
试一试
你能从中发现什么?
同乘以一个正数,不等号方向不变,
同乘以一个负数不等号方向改变,
同乘以0的时候相等.
结论:
不等式的性质2
如果a>b,并且c >0,那么ac > bc, .
不等式的性质3
如果a>b,并且c <0,那么ac < bc, .
也就是说,不等式的两边都____________ 同一个
正数,不等号的方向_______;
不等式的两边都_____________同一个
负数,不等号的方向________.
乘以(或除以)
不变
乘以(或除以)
改变
比较等式的性质和不等式的性质的异同
等式两边都加上或减去同一个数或整式,所得
结果仍是等式.
等式两边都乘以或除以同一个不等于零的数,所得结果仍是等式
不等式的两边都加上(或减去)同一个数或同一个
整式,不等号方向不变.
不等式的两边都乘以或除以同一正数,不等号方向不变.
不等式的两边都乘以或除以同一负数,不等号方向改变.
解:方程的两边都加上7,等式仍然成立,所以
与解方程一样,解不等式的过程,就是要将不等式变形成x>a 或x
解不等式:x -7<8
x-7+7=8+7,
解:不等式的两边都
加上7,不等号的方向
不变,所以
x-7+7 8+7,
x< 8+7,
<
x=8+7,
x=15.
x< 15.
例题精析
例1 解不等式:
(1) x+7>8; (2) 3x<2x-7.
解:(1)不等式的两边都减去7,不等号的方向不变,
∴ x+7 -7 >8 -7,
∴ x>1.
(2)不等式的两边都减去2x,不等号的方向不变,
∴ 3x -2x <2x-7 -2x,
∴ x <-7 .
这两小题中不等式的变形
与方程的什么变形类似?
移项
将不等式的某些项改变符号后移到不等式的
另一边,不等式的方向不变.
解下列不等式:
(1) x-2<3 ; (2) x+1≥7;
(3) 4+5x≤4x; (4) 7x+15>6x+13.
随堂练习
解:(1)不等式的两边都加上2,不等号的方向不变,
∴ x -2+2 <3+2,
∴ x <5.
(2)不等式的两边都减去1,不等号的方向不变,
∴ x+1 -1≥7 -1,
∴ x≥6.
(3)不等式的两边都加上(-4x-4),不等号的方向不变,
∴ 4+5x -4x-4 ≤4x -4x-4,
∴ x≤-4.
(4)不等式的两边都加上(-6x-15),不等号的方向不变,
∴ 7x+15 -6x-15 >6x+13 -6x-15,
∴ x >-2.
例题精析
例2 解不等式:
(1) ; (2) -2x<6.
解:(1)不等式的两边都乘以2,不等号的方向不变,
∴ x> - 6.
(2)不等式的两边都除以-2,不等号的方向改变,
∴ (-2x)÷ (-2) > 6 ÷(-2),
∴ x >-3 .
系数化为1
这两小题中不等式的变形
与方程的什么变形类似?
有什么不同?
要注意系数的正负!
正不变,负改变.
解下列不等式,并将解集在数轴上表示出来:
-2x>4; (2) 3x≤0;
(3) 5x>20; (4) -4x≥-12.
随堂练习
(1)不等式的两边都除以-2,不等号的方向改变,
∴ (-2x)÷ (-2) < 4 ÷(-2),
∴ x < -2.
(2)不等式的两边都除以3,不等号的方向不变,
∴ 3x÷ 3 ≤ 0÷3,
∴ x≤ 0 .
(3)不等式的两边都除以5,不等号的方向不变,
∴ 5x÷ 5> 20 ÷5,
∴ x> 4.
(4)不等式的两边都除以-4,不等号的方向改变,
∴ (-4x)÷ (-4) ≤ (-12) ÷(-4),
∴ x≤ 3 .
一.不等式的性质
课堂小结
性质1
如果a>b,那么a+c > b+c, a-c >b-c.
性质2
性质3
如果a>b,并且c >0,那么ac > bc, .
如果a>b,并且c <0,那么ac < bc, .
二. 解一元一次不等式的过程,类似于解一元一次
方程,就是将不等式进行一系列的变形,最终转化
成x >a( x≥a)或x
1.练习作业:学习检测P45-46 第1至21题
书面课本P61 习题8.2 1
2.课外学习任务:
预习课本P58 8.2.3 解一元一次不等式
教学反馈:
作业存在的主要问题:
