华东师大版七年级下册数学课件:9.1.1 认识三角形(共27张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学课件:9.1.1 认识三角形(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 00:00:00 | ||
图片预览





文档简介
第9章 多 边 形
9.1 三 角 形
1.认识三角形
教学目标
教学重点与难点
重点:三角形及其有关概念与分类.
难点:三角形的有关概念与分类.
1. 理解三角形的概念.
2.掌握三角形的边、顶点、内角、外角等有关概念.
3.掌握三角形按角和按边的分类.
4.能从所给的图中找出三角形.
探究发现
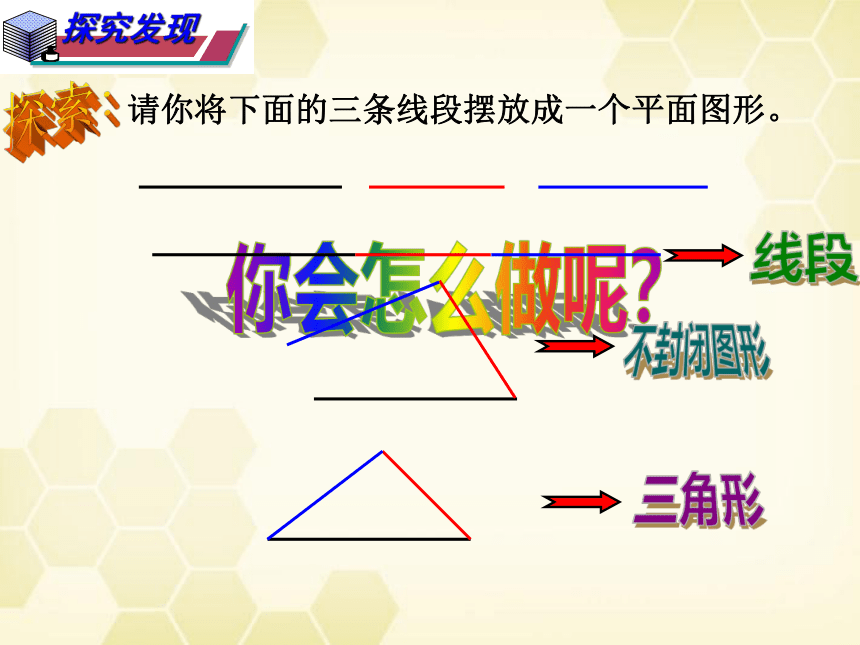
请你将下面的三条线段摆放成一个平面图形。
归纳总结
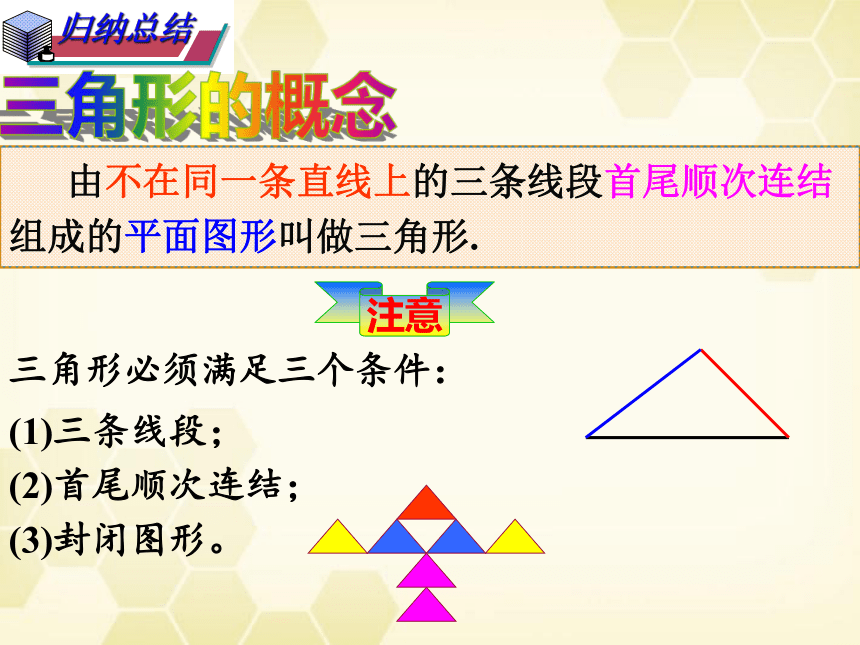
由不在同一条直线上的三条线段首尾顺次连结
组成的平面图形叫做三角形.
三角形必须满足三个条件:
注意
(1)三条线段;
(2)首尾顺次连结;
(3)封闭图形。
探究发现
(一)三角形的相关概念
A
B
C
(1)相邻两边的交点叫做三角形的顶点;
用一个大写字母表示:如A、B、C
顶点
(2)组成三角形的三条线段叫做三角形的边;
边
记作:边AB,边BC,边AC
(3)每两条边所组成的角叫做三角形的内角 ;
记作:∠BAC,∠ABC,∠ACB
内角
(二)三角形的表示方法:
三角形用“△”表示.
记作:△ABC
读作:三角形ABC
一个三角形有多少个顶点?多少条边?
多少个内角?
∠A所对的边记为边a;
∠B所对的边记为边b;
∠C所对的边记为边c.
A
B
C
(三)三角形的边的表示方法
a
b
c
探究发现
A
B
C
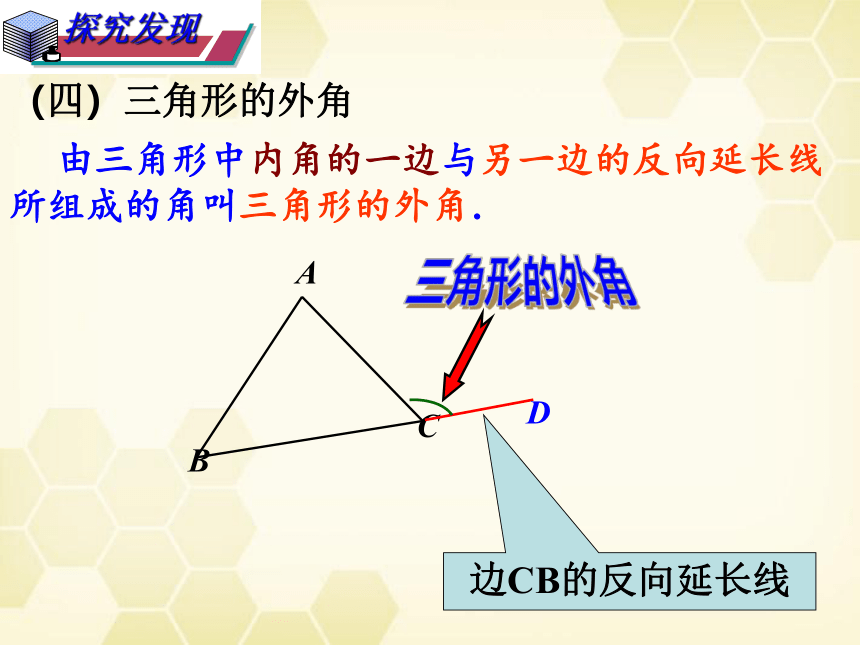
(四)三角形的外角
D
由三角形中内角的一边与另一边的反向延长线所组成的角叫三角形的外角.
探究发现
边CB的反向延长线
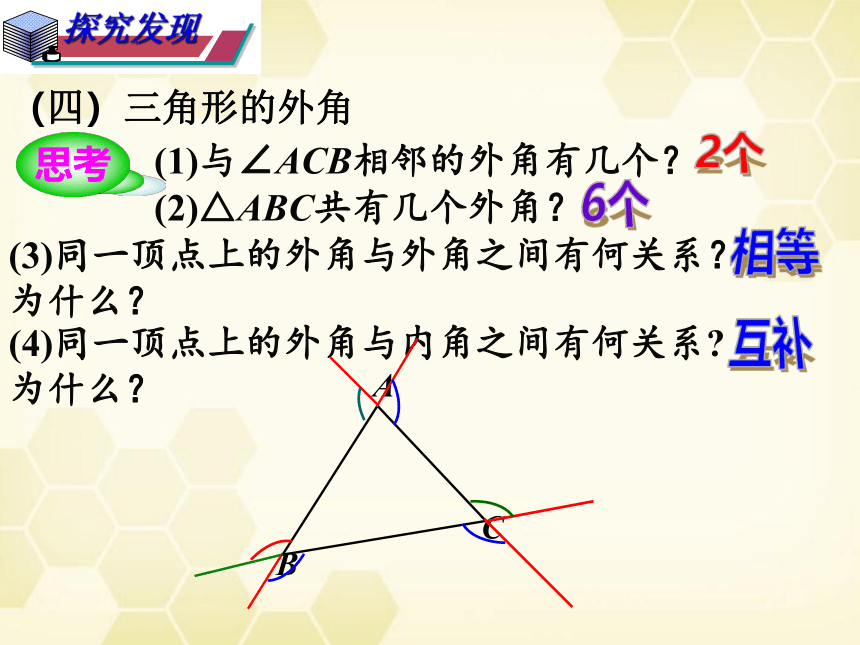
(四)三角形的外角
A
B
C
思考
(1)与∠ACB相邻的外角有几个?
(2)△ABC共有几个外角?
(3)同一顶点上的外角与外角之间有何关系?
为什么?
(4)同一顶点上的外角与内角之间有何关系?
为什么?
探究发现
归纳总结
A
B
C
D
例题精析
(1)图中有几个三角形?并把它们表示出来;
(2)指出△ADC的三个内角、三条边;
A
B
C
D
(3)∠ADC能写成∠D吗?∠ACD能写成∠C吗?为什么?
(4)有人说CD是△ACD和△ABC的公共的边,对吗?
AD是△ACD和△ABD的公共边,对吗?
(5)∠BDA是△ACD的什么角?
E
此时图中共有多少个三角形?
例1 观察下图,解决下列问题:
(1)△ABC中有一条线段AD时,共有 个三角形;
A
B
C
D
E
A
B
C
D
E
A
B
C
D
F
(2)△ABC中有两条线段AD、AE时,共有 个三角形;
(3)△ABC中有三条线段AD、AE、AF时,共有 个三角形;
(4)△ABC中有四条线段时,共有 个三角形;
(5)△ABC中有n条线段时,共有 个三角形。
例2 观察下图,解决下列问题:
1.(1)图中以BC为边的三角形共有______个;
它们分别______________________________.
(2)在△ABD中,
∠A是_______边的对角,
∠ADB是△_____的内角,又是________________的一个外角.
D
B
E
C
F
A
4
△BCF, △ BCE, △ BCD, △ BCA
△FDC 或△BDC
ABD
BD
随堂练习
2.如图所示,
(1)以AE为边的三角形有____________________;
(2)∠B分别是△ABD、△ABE、△ABC中
边_________________ 的对角;
(3)△ADE的三条边分别是_______________;
三个内角分别是___________________________;
(4)∠ADC是___________________的内角,
是________的外角.
△ABE、△ADE、△AEC
AD、AE、AC
AD、DE、EA
∠ADE、∠DEA、∠EAD
△ADC、△ADE
△ABD
下图中,三个三角形的内角各有什么特点?
(1) (2) (3)
三角形可以按角来分类:
所有内角都是锐角
三角形
锐角三角形
直角三角形
钝角三角形
有一个内角是直角
有一个内角是钝角
学习新知
┐
三个内角
都是锐角
有一个内角
是直角
有一个内角
是钝角
下图中,三个三角形的边各有什么特点?
三角形可以按边来分类:
三条边都不相等
三角形
不等边三角形
等腰三角形
等边三角形
有两条边相等
三条边都相等
(1) (2) (3)
等边三角形是不是等腰三角形?
学习新知
三边互
不相等
有两条
边相等
三边都
相等
等腰三角形中,相等的两边叫腰,另一边叫底,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
腰
腰
底
顶
角
底角
底角
等腰三角形
等边三角形
(或正三角形)
直角三角形
锐角三角形
钝角三角形
不等边三角形
a
c
b
a
a
a
a
a
b
三角形的分类
例题精析
例3 下列叙述中正确的是( ).
A.三角形可分为等腰三角形和等边三角形
B.等腰三角形是等边三角形
C.等边三角形是特殊的等腰三角形
D.三角形可分为三边都不相等的三角形和三边
都相等的三角形
C
例4 已知△ABC的一个外角为50°,则△ABC一定
是( ).
A.锐角三角形 B.钝角三角形
C.直角三角形 D.锐角或钝角三角形
B
例5 观察下面的三角形,并把它们的标号填在相应
的圈内.
例题精析
①
②
③
④
⑤
⑥
⑦
随堂练习
1.在一个三角形的三个内角中,至少有( ).
A.一个钝角 B.一个直角
C.一个锐角 D.两个锐角
2.如果三角形的一个外角等于和它相邻的内角,
那么这个三角形是( ).
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不确定
D
B
3.如图,过A、B、C、D、E五个点中任意三点画
三角形,
(1)其中以AB为一边可以画出 个三角形;
(2)其中以C为顶点可以画出 个三角形.
△ABC、△ABD、△ABE
3
△ABC、△BDC、△BEC、△AEC、△ADC、△DEC
6
4.(1)如图①,AC是正方形ABCD的对角线,则图中的直角三角形有2个,它们分别是△ABC、△ACD;
图中的等腰三角形有 个,
它们分别是 _____________________;
(2)如图②,AB=AC,AD=BD=DE=AE=CE.
①写出图②中所有的等腰三角形;
②写出图②中所有的等边三角形.
△ABC、△ACD
2
△ABC、△ABD、△ADE、△ACE.
△ADE
课堂小结
一.三角形的概念:
由不在同一条直线上的三条线段首尾顺次连结
组成的平面图形叫做三角形.
二.三角形的相关概念:
(1)相邻两边的交点叫做三角形的顶点;
(2)组成三角形的三条线段叫做三角形的边;
(3)每两条边所组成的角叫做三角形的内角 ;
(4)由三角形中内角的一边与另一边的反向延长线所组成的角叫三角形的外角.
三.三角形的表示方法:
三角形用“△”表示.
记作:△ABC
读作:三角形ABC
(1) (2) (3)
三角形可以按角来分类:
所有内角都是锐角
三角形
锐角三角形
直角三角形
钝角三角形
有一个内角是直角
有一个内角是钝角
┐
四.三角形的分类:
三角形可以按边来分类:
三条边都不相等
三角形
不等边三角形
等腰三角形
等边三角形
有两条边相等
三条边都相等
(1) (2) (3)
四.三角形的分类:
作业与课外学习任务
1.练习作业:学习检测P54-55 第1至10题
书面课本P75 练习 1,2
2.课外学习任务:
预习P75 9.1 三角形的中线、角平分线、高
教学反馈:
作业存在的主要问题:
9.1 三 角 形
1.认识三角形
教学目标
教学重点与难点
重点:三角形及其有关概念与分类.
难点:三角形的有关概念与分类.
1. 理解三角形的概念.
2.掌握三角形的边、顶点、内角、外角等有关概念.
3.掌握三角形按角和按边的分类.
4.能从所给的图中找出三角形.
探究发现
请你将下面的三条线段摆放成一个平面图形。
归纳总结
由不在同一条直线上的三条线段首尾顺次连结
组成的平面图形叫做三角形.
三角形必须满足三个条件:
注意
(1)三条线段;
(2)首尾顺次连结;
(3)封闭图形。
探究发现
(一)三角形的相关概念
A
B
C
(1)相邻两边的交点叫做三角形的顶点;
用一个大写字母表示:如A、B、C
顶点
(2)组成三角形的三条线段叫做三角形的边;
边
记作:边AB,边BC,边AC
(3)每两条边所组成的角叫做三角形的内角 ;
记作:∠BAC,∠ABC,∠ACB
内角
(二)三角形的表示方法:
三角形用“△”表示.
记作:△ABC
读作:三角形ABC
一个三角形有多少个顶点?多少条边?
多少个内角?
∠A所对的边记为边a;
∠B所对的边记为边b;
∠C所对的边记为边c.
A
B
C
(三)三角形的边的表示方法
a
b
c
探究发现
A
B
C
(四)三角形的外角
D
由三角形中内角的一边与另一边的反向延长线所组成的角叫三角形的外角.
探究发现
边CB的反向延长线
(四)三角形的外角
A
B
C
思考
(1)与∠ACB相邻的外角有几个?
(2)△ABC共有几个外角?
(3)同一顶点上的外角与外角之间有何关系?
为什么?
(4)同一顶点上的外角与内角之间有何关系?
为什么?
探究发现
归纳总结
A
B
C
D
例题精析
(1)图中有几个三角形?并把它们表示出来;
(2)指出△ADC的三个内角、三条边;
A
B
C
D
(3)∠ADC能写成∠D吗?∠ACD能写成∠C吗?为什么?
(4)有人说CD是△ACD和△ABC的公共的边,对吗?
AD是△ACD和△ABD的公共边,对吗?
(5)∠BDA是△ACD的什么角?
E
此时图中共有多少个三角形?
例1 观察下图,解决下列问题:
(1)△ABC中有一条线段AD时,共有 个三角形;
A
B
C
D
E
A
B
C
D
E
A
B
C
D
F
(2)△ABC中有两条线段AD、AE时,共有 个三角形;
(3)△ABC中有三条线段AD、AE、AF时,共有 个三角形;
(4)△ABC中有四条线段时,共有 个三角形;
(5)△ABC中有n条线段时,共有 个三角形。
例2 观察下图,解决下列问题:
1.(1)图中以BC为边的三角形共有______个;
它们分别______________________________.
(2)在△ABD中,
∠A是_______边的对角,
∠ADB是△_____的内角,又是________________的一个外角.
D
B
E
C
F
A
4
△BCF, △ BCE, △ BCD, △ BCA
△FDC 或△BDC
ABD
BD
随堂练习
2.如图所示,
(1)以AE为边的三角形有____________________;
(2)∠B分别是△ABD、△ABE、△ABC中
边_________________ 的对角;
(3)△ADE的三条边分别是_______________;
三个内角分别是___________________________;
(4)∠ADC是___________________的内角,
是________的外角.
△ABE、△ADE、△AEC
AD、AE、AC
AD、DE、EA
∠ADE、∠DEA、∠EAD
△ADC、△ADE
△ABD
下图中,三个三角形的内角各有什么特点?
(1) (2) (3)
三角形可以按角来分类:
所有内角都是锐角
三角形
锐角三角形
直角三角形
钝角三角形
有一个内角是直角
有一个内角是钝角
学习新知
┐
三个内角
都是锐角
有一个内角
是直角
有一个内角
是钝角
下图中,三个三角形的边各有什么特点?
三角形可以按边来分类:
三条边都不相等
三角形
不等边三角形
等腰三角形
等边三角形
有两条边相等
三条边都相等
(1) (2) (3)
等边三角形是不是等腰三角形?
学习新知
三边互
不相等
有两条
边相等
三边都
相等
等腰三角形中,相等的两边叫腰,另一边叫底,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
腰
腰
底
顶
角
底角
底角
等腰三角形
等边三角形
(或正三角形)
直角三角形
锐角三角形
钝角三角形
不等边三角形
a
c
b
a
a
a
a
a
b
三角形的分类
例题精析
例3 下列叙述中正确的是( ).
A.三角形可分为等腰三角形和等边三角形
B.等腰三角形是等边三角形
C.等边三角形是特殊的等腰三角形
D.三角形可分为三边都不相等的三角形和三边
都相等的三角形
C
例4 已知△ABC的一个外角为50°,则△ABC一定
是( ).
A.锐角三角形 B.钝角三角形
C.直角三角形 D.锐角或钝角三角形
B
例5 观察下面的三角形,并把它们的标号填在相应
的圈内.
例题精析
①
②
③
④
⑤
⑥
⑦
随堂练习
1.在一个三角形的三个内角中,至少有( ).
A.一个钝角 B.一个直角
C.一个锐角 D.两个锐角
2.如果三角形的一个外角等于和它相邻的内角,
那么这个三角形是( ).
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不确定
D
B
3.如图,过A、B、C、D、E五个点中任意三点画
三角形,
(1)其中以AB为一边可以画出 个三角形;
(2)其中以C为顶点可以画出 个三角形.
△ABC、△ABD、△ABE
3
△ABC、△BDC、△BEC、△AEC、△ADC、△DEC
6
4.(1)如图①,AC是正方形ABCD的对角线,则图中的直角三角形有2个,它们分别是△ABC、△ACD;
图中的等腰三角形有 个,
它们分别是 _____________________;
(2)如图②,AB=AC,AD=BD=DE=AE=CE.
①写出图②中所有的等腰三角形;
②写出图②中所有的等边三角形.
△ABC、△ACD
2
△ABC、△ABD、△ADE、△ACE.
△ADE
课堂小结
一.三角形的概念:
由不在同一条直线上的三条线段首尾顺次连结
组成的平面图形叫做三角形.
二.三角形的相关概念:
(1)相邻两边的交点叫做三角形的顶点;
(2)组成三角形的三条线段叫做三角形的边;
(3)每两条边所组成的角叫做三角形的内角 ;
(4)由三角形中内角的一边与另一边的反向延长线所组成的角叫三角形的外角.
三.三角形的表示方法:
三角形用“△”表示.
记作:△ABC
读作:三角形ABC
(1) (2) (3)
三角形可以按角来分类:
所有内角都是锐角
三角形
锐角三角形
直角三角形
钝角三角形
有一个内角是直角
有一个内角是钝角
┐
四.三角形的分类:
三角形可以按边来分类:
三条边都不相等
三角形
不等边三角形
等腰三角形
等边三角形
有两条边相等
三条边都相等
(1) (2) (3)
四.三角形的分类:
作业与课外学习任务
1.练习作业:学习检测P54-55 第1至10题
书面课本P75 练习 1,2
2.课外学习任务:
预习P75 9.1 三角形的中线、角平分线、高
教学反馈:
作业存在的主要问题:
