华东师大版七年级下册数学课件:9.1.1 认识三角形
文档属性
| 名称 | 华东师大版七年级下册数学课件:9.1.1 认识三角形 |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 00:00:00 | ||
图片预览






文档简介
第9章 多 边 形
9.1 三 角 形
1(2).认识三角形
教学目标
教学重点与难点
重点:三角形的中线、角平分线、高及其特征.
难点:三角形的中线、角平分线、高概念.
1. 理解三角形的中线、角平分线、高的概念.
2.掌握三角形的三条中线、角平分线、高的特征.
3.会做出三角形的三条中线、角平分线、高.
一.三角形的概念:
由不在同一条直线上的三条线段首尾顺次连结
组成的平面图形叫做三角形.
二.三角形的相关概念:
(1)相邻两边的交点叫做三角形的顶点;
(2)组成三角形的三条线段叫做三角形的边;
(3)每两条边所组成的角叫做三角形的内角 ;
(4)由三角形中内角的一边与另一边的反向延长线所组成的角叫三角形的外角.
三.三角形的表示方法:
三角形用“△”表示.
记作:△ABC
读作:三角形ABC
温故夯基
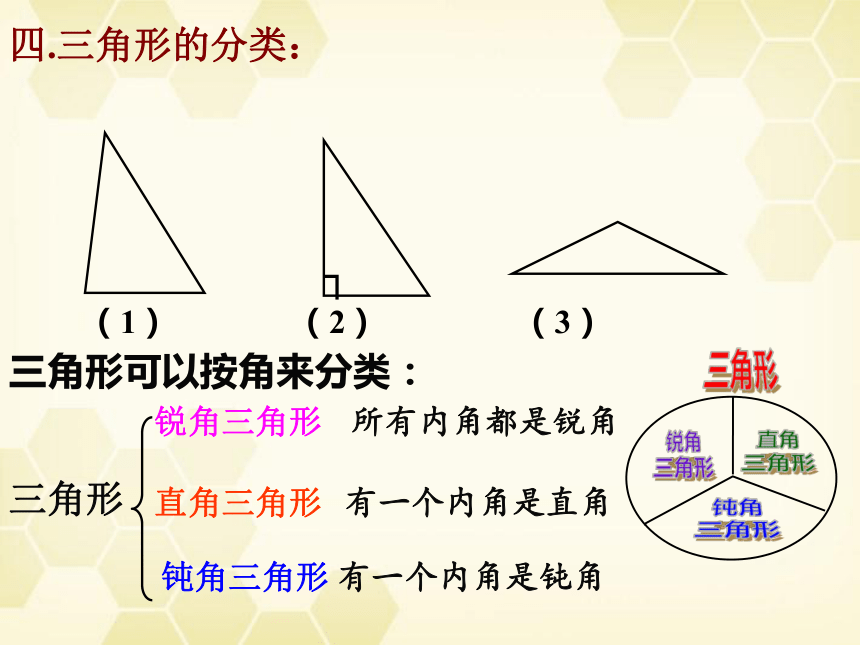
(1) (2) (3)
三角形可以按角来分类:
所有内角都是锐角
三角形
锐角三角形
直角三角形
钝角三角形
有一个内角是直角
有一个内角是钝角
┐
四.三角形的分类:
三角形可以按边来分类:
三条边都不相等
三角形
不等边三角形
等腰三角形
等边三角形
有两条边相等
三条边都相等
(1) (2) (3)
四.三角形的分类:
1.如图,以AB为边的三角形有 ;
以AD为边的三角形有 ;
△ABD的一个外角是 .
巩固练习
2.如图,图中共有 个三角形,其中以BC为一边的三角形是 ;
以∠A为一个内角的三角形是 .
(第1题图)
(第2题图)
△ABD ,△ABC
△ABD ,△ACD
∠ADC
5
△ABC ,△DBC, △EBC
△ABC ,△ABE
3.如图,已知∠ACB=100o,△ABC的
一个外角是∠ ,它的度数为 .
A
B
C
D
ACD
80o
4.下列说法错误的是( ).
A. 三个角都是锐角的三角形是锐角三角形
B. 有一个角是直角的三角形是直角三角形
C. 钝角三角形中只有一个内角是钝角
D. 有一个外角是锐角的三角形是锐角三角形
D
5.至少有两边相等的三角形是( ).
A.等边三角形 B.等腰三角形
C.等腰直角三角形 D. 锐角三角形
B
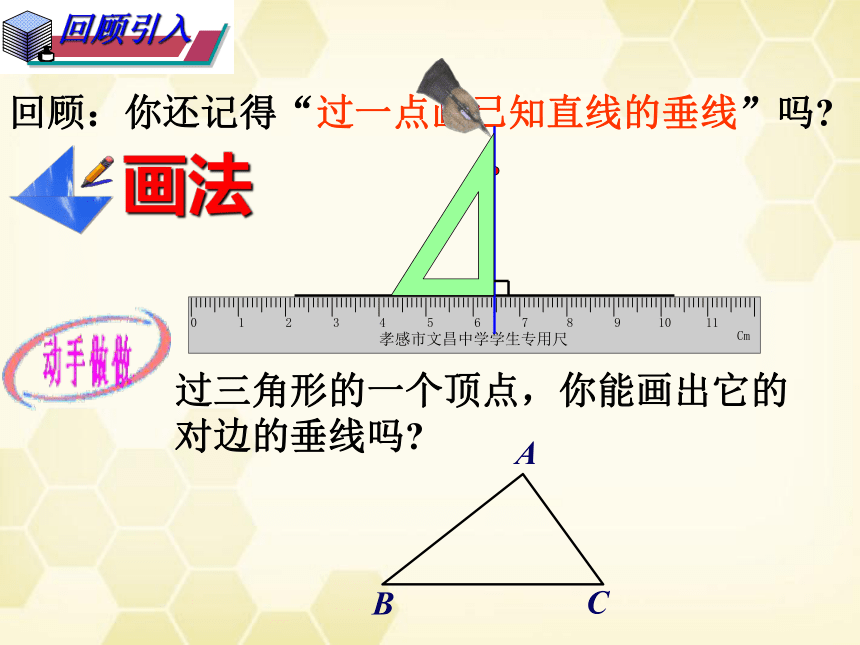
回顾:你还记得“过一点画已知直线的垂线”吗?
画法
过三角形的一个顶点,你能画出它的
对边的垂线吗?
B
A
C
回顾引入
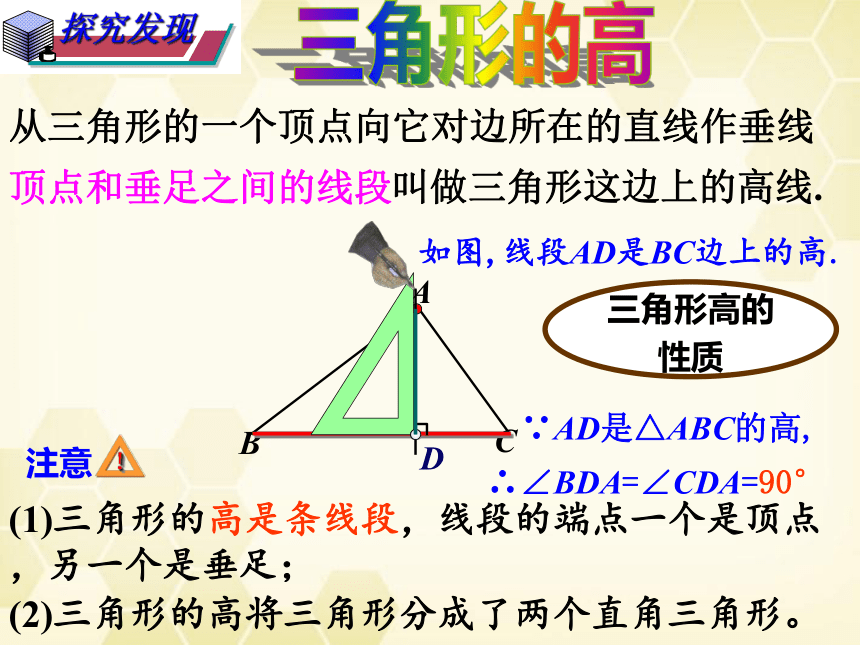
探究发现
从三角形的一个顶点向它对边所在的直线作垂线
A
B
C
顶点和垂足之间的线段
D
叫做三角形这边上的高线.
如图,线段AD是BC边上的高.
注意
!
(1)三角形的高是条线段,线段的端点一个是顶点,另一个是垂足;
(2)三角形的高将三角形分成了两个直角三角形。
三角形高的
性质
∵AD是△ABC的高,
∴∠BDA=∠CDA=90°
每人在练习本上画一个锐角三角形。
(1)请你画出这个三角形的三条边上的高;
O
A
B
C
D
E
F
(2)这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
锐角三角形的三条高交于同一点.
锐角三角形的三条高是在三角形的内部还是外部?
锐角三角形的三条高都在三角形的内部.
探究发现
A
B
C
每人在练习本上画一个直角三角形。
(1)请你画出直角三角形的三条边上的高;
直角边BC边上的高是 ;
AB
直角边AB边上的高是 ;
BC
斜边AC边上的高是 ;
D
BD
(2)它们有怎样的位置关系?
●
直角三角形的三条高
交于直角顶点.
探究发现
每人在练习本上画一个钝角三角形。
(1)请你画出钝角三角形的三边上的高;
(2)钝角三角形的三条高交于
一点吗?
A
B
C
D
E
F
钝 角三角形的三条高
不相交于一点
(3)它们所在的直线交于一点
吗?
钝角三角形的三条高
所在直线交于一点
探究发现
归纳总结
锐角三角形
直角三角形
钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
1.下列各组图形中,哪一组图形中AD是△ABC的高( ).
A
B
C
D
B
A
B
C
D
C
A
B
C
D
D
A
D
C
B
A
D
B
随堂练习
2.如果一个三角形的三条高的交点恰是三角形的
一个顶点,那么这个三角形是( ).
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 锐角三角形
3.用三角板作△ABC的边BC上的高,下列三角板
的摆放位置正确的是( ).
A B C D
A
4.如图所示,AC⊥BC,CD⊥AB,DE⊥BC,
下列说法中不正确的是( )
A.AC是△ABC的高
B.DE是△BCD的高
C.DE是△ABE的高
D.AD是△ACD的高
C
A
B
C
D
●
●
在三角形中,连接一个顶点与它对边中点的线段叫做三角形这边的中线.
∵ AD是△ABC的中线,
∴BD=CD=
1
2
BC
任意画一个三角形,然后利用刻度尺画出
这个三角形三条边的中线,你发现了什么?
E
F
O
三角形的三条中线相交于一点,交点在三角形的
内部,这个交点叫三角形的重心。
三角形中线的性质
探究发现
随堂练习
1.如图,在△ABC中有四条线段DE,BE,EG,FG,
其中有一条线段是△ABC的中线,则该线段是( ).
A.线段DE B.线段BE
C.线段EG D.线段FG
B
2.如图,D、E分别是△ABC的边AC、BC的中点,
那么下列说法中不正确的是( ).
A.DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BE=EC D.AD=EC,DC=BE
(第1题图)
(第2题图)
D
3.如图,在△ABC中,AD是△ABC的中线,AE是
△ABD的中线,若ED=2 cm,则BC= cm.
8
4.如图,AD,BE,CF是△ABC的三条中线,
则AB=2 =2 ,BD= , AE= .
F
E
D
C
B
A
AF
BF
CD
AC
A
B
C
D
●
●
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
E
F
O
1
2
∵AD是 △ ABC的角平分线,
∴∠ BAD = ∠ CAD =
1
2
∠BAC,
任意画一个三角形,然后利用量角器画出
这个三角形三个角的平分线,你发现什么?
三角形的三条角平分线相交于一点,交点在三角形的内部,这个交点叫做三角形的内心。
∴∠BAC=2∠BAD=2∠CAD.
三角形角平分线的性质
探究发现
三角形的角平分线与角的平分线有什么区别?
思考
三角形的角平分线是一条线段 ,
角的平分线是一条射线.
随堂练习
1.如图,AD、BE、CF为△ABC的三条角平分线,
则∠1= = ,
∠2= = ∠ABC,∠3= = ∠ACB.
∠CAD
∠BAC
∠ABE
∠BCF
2.如图,∠1=∠2,∠3=∠4,下列结论中错误
的是( ).
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.2∠3=∠ACB
D.CE是△ABC的角平分线
D
3.如图,已知CD、CE、CF分别是△ABC的高、
角平分线、中线,则下列各式中错误的是( ).
A.AB=2BF
B.∠ACE= ∠ACB
C.AE=BE
D.CD⊥BE
C
课堂小结
一.三角形的高:
从三角形的一个顶点向它对边所在的直线作垂线,顶点和垂足之间的线段.
锐角三角形的三条高都在三角形的内部,交于同一点.
直角三角形的三条高交于直角顶点.
钝角三角形的三条高不相交于一点,高所在直线交于一点.
三角形的三条高所在直线交于一点.(垂心)
二.三角形的中线:
在三角形中,连接一个顶点与它对边中点的线段.
三角形的三条中线相交于一点,交点在三角形的
内部,这个交点叫三角形的重心。
三.三角形的角平分线:
在三角形中,一个内角的角平分线与它的对边相交,
这个角的顶点与交点之间的线段,叫做三角形的
角平分线.
三角形的三条角平分线相交于一点,交点在三角形
的内部,这个交点叫做三角形的内心。
注意:三角形的角平分线是一条线段 ,
角的平分线是一条射线.
作业与课外学习任务
1.练习作业:学习检测P54-55 第1至10题
书面课本P76 练习 1,2
2.课外学习任务:
预习P76 9.1.2 三角形的内角和与外角和
教学反馈:
作业存在的主要问题:
9.1 三 角 形
1(2).认识三角形
教学目标
教学重点与难点
重点:三角形的中线、角平分线、高及其特征.
难点:三角形的中线、角平分线、高概念.
1. 理解三角形的中线、角平分线、高的概念.
2.掌握三角形的三条中线、角平分线、高的特征.
3.会做出三角形的三条中线、角平分线、高.
一.三角形的概念:
由不在同一条直线上的三条线段首尾顺次连结
组成的平面图形叫做三角形.
二.三角形的相关概念:
(1)相邻两边的交点叫做三角形的顶点;
(2)组成三角形的三条线段叫做三角形的边;
(3)每两条边所组成的角叫做三角形的内角 ;
(4)由三角形中内角的一边与另一边的反向延长线所组成的角叫三角形的外角.
三.三角形的表示方法:
三角形用“△”表示.
记作:△ABC
读作:三角形ABC
温故夯基
(1) (2) (3)
三角形可以按角来分类:
所有内角都是锐角
三角形
锐角三角形
直角三角形
钝角三角形
有一个内角是直角
有一个内角是钝角
┐
四.三角形的分类:
三角形可以按边来分类:
三条边都不相等
三角形
不等边三角形
等腰三角形
等边三角形
有两条边相等
三条边都相等
(1) (2) (3)
四.三角形的分类:
1.如图,以AB为边的三角形有 ;
以AD为边的三角形有 ;
△ABD的一个外角是 .
巩固练习
2.如图,图中共有 个三角形,其中以BC为一边的三角形是 ;
以∠A为一个内角的三角形是 .
(第1题图)
(第2题图)
△ABD ,△ABC
△ABD ,△ACD
∠ADC
5
△ABC ,△DBC, △EBC
△ABC ,△ABE
3.如图,已知∠ACB=100o,△ABC的
一个外角是∠ ,它的度数为 .
A
B
C
D
ACD
80o
4.下列说法错误的是( ).
A. 三个角都是锐角的三角形是锐角三角形
B. 有一个角是直角的三角形是直角三角形
C. 钝角三角形中只有一个内角是钝角
D. 有一个外角是锐角的三角形是锐角三角形
D
5.至少有两边相等的三角形是( ).
A.等边三角形 B.等腰三角形
C.等腰直角三角形 D. 锐角三角形
B
回顾:你还记得“过一点画已知直线的垂线”吗?
画法
过三角形的一个顶点,你能画出它的
对边的垂线吗?
B
A
C
回顾引入
探究发现
从三角形的一个顶点向它对边所在的直线作垂线
A
B
C
顶点和垂足之间的线段
D
叫做三角形这边上的高线.
如图,线段AD是BC边上的高.
注意
!
(1)三角形的高是条线段,线段的端点一个是顶点,另一个是垂足;
(2)三角形的高将三角形分成了两个直角三角形。
三角形高的
性质
∵AD是△ABC的高,
∴∠BDA=∠CDA=90°
每人在练习本上画一个锐角三角形。
(1)请你画出这个三角形的三条边上的高;
O
A
B
C
D
E
F
(2)这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
锐角三角形的三条高交于同一点.
锐角三角形的三条高是在三角形的内部还是外部?
锐角三角形的三条高都在三角形的内部.
探究发现
A
B
C
每人在练习本上画一个直角三角形。
(1)请你画出直角三角形的三条边上的高;
直角边BC边上的高是 ;
AB
直角边AB边上的高是 ;
BC
斜边AC边上的高是 ;
D
BD
(2)它们有怎样的位置关系?
●
直角三角形的三条高
交于直角顶点.
探究发现
每人在练习本上画一个钝角三角形。
(1)请你画出钝角三角形的三边上的高;
(2)钝角三角形的三条高交于
一点吗?
A
B
C
D
E
F
钝 角三角形的三条高
不相交于一点
(3)它们所在的直线交于一点
吗?
钝角三角形的三条高
所在直线交于一点
探究发现
归纳总结
锐角三角形
直角三角形
钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
1.下列各组图形中,哪一组图形中AD是△ABC的高( ).
A
B
C
D
B
A
B
C
D
C
A
B
C
D
D
A
D
C
B
A
D
B
随堂练习
2.如果一个三角形的三条高的交点恰是三角形的
一个顶点,那么这个三角形是( ).
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 锐角三角形
3.用三角板作△ABC的边BC上的高,下列三角板
的摆放位置正确的是( ).
A B C D
A
4.如图所示,AC⊥BC,CD⊥AB,DE⊥BC,
下列说法中不正确的是( )
A.AC是△ABC的高
B.DE是△BCD的高
C.DE是△ABE的高
D.AD是△ACD的高
C
A
B
C
D
●
●
在三角形中,连接一个顶点与它对边中点的线段叫做三角形这边的中线.
∵ AD是△ABC的中线,
∴BD=CD=
1
2
BC
任意画一个三角形,然后利用刻度尺画出
这个三角形三条边的中线,你发现了什么?
E
F
O
三角形的三条中线相交于一点,交点在三角形的
内部,这个交点叫三角形的重心。
三角形中线的性质
探究发现
随堂练习
1.如图,在△ABC中有四条线段DE,BE,EG,FG,
其中有一条线段是△ABC的中线,则该线段是( ).
A.线段DE B.线段BE
C.线段EG D.线段FG
B
2.如图,D、E分别是△ABC的边AC、BC的中点,
那么下列说法中不正确的是( ).
A.DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BE=EC D.AD=EC,DC=BE
(第1题图)
(第2题图)
D
3.如图,在△ABC中,AD是△ABC的中线,AE是
△ABD的中线,若ED=2 cm,则BC= cm.
8
4.如图,AD,BE,CF是△ABC的三条中线,
则AB=2 =2 ,BD= , AE= .
F
E
D
C
B
A
AF
BF
CD
AC
A
B
C
D
●
●
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
E
F
O
1
2
∵AD是 △ ABC的角平分线,
∴∠ BAD = ∠ CAD =
1
2
∠BAC,
任意画一个三角形,然后利用量角器画出
这个三角形三个角的平分线,你发现什么?
三角形的三条角平分线相交于一点,交点在三角形的内部,这个交点叫做三角形的内心。
∴∠BAC=2∠BAD=2∠CAD.
三角形角平分线的性质
探究发现
三角形的角平分线与角的平分线有什么区别?
思考
三角形的角平分线是一条线段 ,
角的平分线是一条射线.
随堂练习
1.如图,AD、BE、CF为△ABC的三条角平分线,
则∠1= = ,
∠2= = ∠ABC,∠3= = ∠ACB.
∠CAD
∠BAC
∠ABE
∠BCF
2.如图,∠1=∠2,∠3=∠4,下列结论中错误
的是( ).
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.2∠3=∠ACB
D.CE是△ABC的角平分线
D
3.如图,已知CD、CE、CF分别是△ABC的高、
角平分线、中线,则下列各式中错误的是( ).
A.AB=2BF
B.∠ACE= ∠ACB
C.AE=BE
D.CD⊥BE
C
课堂小结
一.三角形的高:
从三角形的一个顶点向它对边所在的直线作垂线,顶点和垂足之间的线段.
锐角三角形的三条高都在三角形的内部,交于同一点.
直角三角形的三条高交于直角顶点.
钝角三角形的三条高不相交于一点,高所在直线交于一点.
三角形的三条高所在直线交于一点.(垂心)
二.三角形的中线:
在三角形中,连接一个顶点与它对边中点的线段.
三角形的三条中线相交于一点,交点在三角形的
内部,这个交点叫三角形的重心。
三.三角形的角平分线:
在三角形中,一个内角的角平分线与它的对边相交,
这个角的顶点与交点之间的线段,叫做三角形的
角平分线.
三角形的三条角平分线相交于一点,交点在三角形
的内部,这个交点叫做三角形的内心。
注意:三角形的角平分线是一条线段 ,
角的平分线是一条射线.
作业与课外学习任务
1.练习作业:学习检测P54-55 第1至10题
书面课本P76 练习 1,2
2.课外学习任务:
预习P76 9.1.2 三角形的内角和与外角和
教学反馈:
作业存在的主要问题:
