华东师大版七年级下册数学课件:7.2(3) 二元一次方程组的解法(共22张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学课件:7.2(3) 二元一次方程组的解法(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 17:31:17 | ||
图片预览








文档简介
第7章 一次方程组
7.2 二元一次方程组的解法
2.加减消元法
教学目标
教学重点与难点
重点:理解并掌握加减消元法解二元一次方程组.
难点:理解解方程组的基本思想是“消元”,会化二元
一次方程组为一元一次方程.
1.使学生通过探索,逐步发现解方程的基本思想
是“消元”,化二元一次方程组为一元一次方程.
2.使学生了解“加减消元法”,并掌握加减消元法解二元一次方程组.
3.通过加减消元,使学生进一步理解把“未知”转化
为“已知”,和复杂问题转化为简单问题思想方法.
温故夯基
一.代入消元法解二元一次方程组的基本步骤:
(1)从方程组中选取一个未知数系数比较简单的方程;
(2)用一个未知数的代数式表示另一个未知数;
(3)把代数式代入到另一个方程,得到一个一元一次方程;
(4)解一元一次方程,求出未知数的值;
(5)把未知数的值代入代数式,求出另一个未知数的值;
(6)写出方程组的解.
二.用代入法解二元一次方程组的两种类型:
1.未知数的系数含1或-1的方程组;
2.未知数的系数不含1或-1的方程组.
巩固练习
1.解下列方程组:
解:由① 得:x=-2y.
①
②
③
将 ③代入 ②,得:
3(-2y)+4y=6.
解得:y=-3.
将y=-3代入③,得:x=6.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:y=-1.
将y=-1代入③,得:x=7.
学习新知
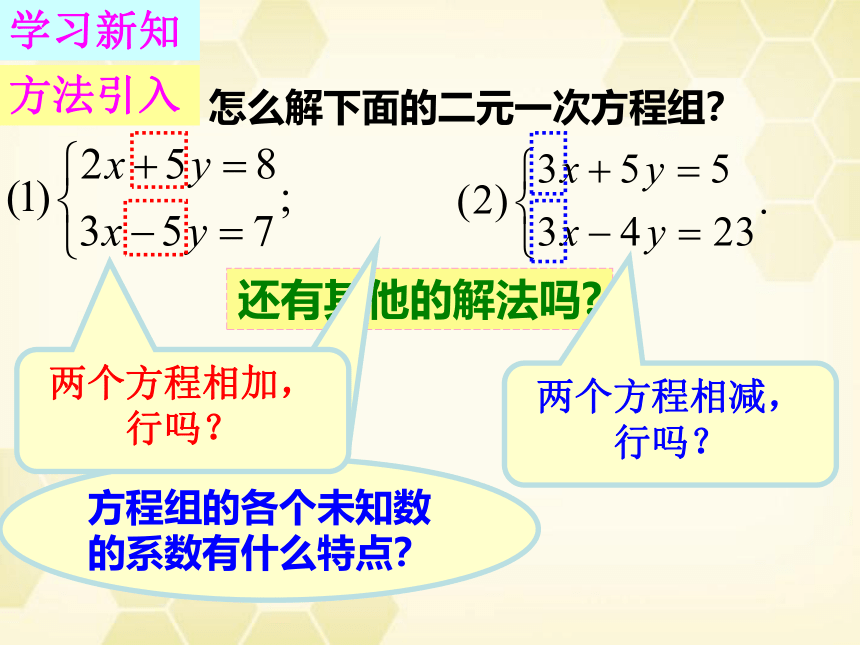
怎么解下面的二元一次方程组?
方法引入
还有其他的解法吗?
方程组的各个未知数的系数有什么特点?
两个方程相加,行吗?
两个方程相减,行吗?
例题精析
例1 解下列方程组:
①
②
解:① + ②得:
5x=15.
∴ x=3.
将x=3代入①,得:
2×3+5y=8.
解得:
解:① - ②得:
①
②
9y=-18.
∴ y=-2.
将y=-2代入①,得:
3x+5×(-2)=5.
解得:
x=5.
两个二元一次方程中同一个未知数的系数相同或
相反时,将两个方程两边分别相减或相加就能消去
这个未知数,得到一个一元一次方程,这种方法
叫做加减消元法,简称加减法.
加减消元法
方法总结
例2 解下列方程组:
①
②
解:① + ②得:
7x=14.
∴ x=2.
将x=2代入①,得:
3×2+7y=9.
解得:
解: ② - ①得:
①
②
7y=-14.
∴ y=-2.
将y=-2代入①,得:
2x-5×(-2)=9.
解得:
随堂练习
①
②
解:① + ②得:
8x=8.
∴ x=1.
将x=1代入①,得:
5×1+y=7.
∴ y=2.
①
②
解: ② - ①得:
9y=9.
∴ y=1.
将y=1代入①,得:
4x-3×1=5.
∴ x=2.
解:① - ②得:
①
②
14y=-14.
∴ y=-1.
将y=-1代入①,得:
6x+7×(-1)=5.
∴ x=2.
①
②
解:① + ②得:
2y=2.
∴ y=1.
将y=1代入①,得:
0.5x-3×1=-1.
∴ x=4.
解:① - ②得:
①
②
5y=10.
∴ y=2.
将y=2代入①,得:
5x+3×2=6.
∴ x=0.
①
②
解:① + ②得:
4x=4.
∴ x=1.
将x=1代入①,得:
1+2y=9.
∴ y=4.
例3 已知 是关于x,y的二元一次方程组
的一组解,求a+b的值.
解:
解方程组得:
∴ a+b=2+3=5.
已知关于x,y的二元一次方程组
的解为 ,求a-2b的值.
解:
解方程组得:
∴ a-2b=
随堂练习
=2.
学习新知
例4 解方程组:
直接相加或相加
能否消去未知数?
①
②
能不能化为未知数
相同或相反的类型?
最小公倍数
解:①×3 + ②×2得:
19x=114.
∴ x=6.
将x=6代入②,得:
30+6y=42.
∴ y=2.
能否先消去x再求解?
怎么做?
学习新知
例4 解方程组:
①
②
最小公倍数
解: ②×3 - ①×5得:
38y=76.
∴ y=2.
将y=2代入②,得:
5x+12=42.
∴ x=6.
用加减消元法解二元一次方程组的基本步骤:
方法总结
(1)把一个方程或两个方程的两边同乘以适当的数,使两个方程中的某一个未知数的系数的绝对值相等;
(2)把所得的两个方程的两边分别相加或相减,
消去一个未知数,得到一个一元一次方程;
(3)解这个方程,求得一个未知数的值;
(4)把所求得的未知数的值代入方程组中某一个
方程,求出另一个未知数的值;
(5)把求得的未知数的值写成 的形式.
例题精析
例5 解方程组:
①
②
37x=111.
∴ x=3.
将x=3代入②,得:
21+4y=-15.
∴ y=-9.
解:①×4 + ②×3得:
随堂练习
①
②
解:①×3 + ②×2得:
13x=52.
∴ x=4.
将x=4代入②,得:
8+3y=17.
∴ y=3.
①
②
解: ① +②× 2 得:
14x=28.
∴ x=2.
将x=2代入②,得:
10+y=7.
∴ y=-3.
随堂练习
①
②
解:①×7 + ②×3得:
16x=160.
∴ x=10.
将x=10代入②,得:
30+7y=100.
∴ y=10.
①
②
解: ① +②× 2 得:
14x=28.
∴ x=2.
将x=2代入②,得:
10+y=7.
∴ y=-3.
随堂练习
解下列方程组:
①
②
解:将① 代入②,得:
(3y+2)+3y=8,
解得:
y=1.
将y=1代入①,得:
x=5.
解:将② 代入①,得:
①
②
4x-3(7-5x)=17,
解得:
x=2.
将x=2代入②,得:
y= - 3.
①
②
解:由①得:
x=y-5 . ③
将③ 代入②,得:
3(y-5)+2y=10,
解得:
y=5.
将y=5代入③,得:
x=0.
①
②
解:由②得:
y=2x-3.2 . ③
将③ 代入①,得:
2x-7(2x-3.2)=8,
解得:
x=1.2 .
将x=1.2代入③,得:
y=-0.8 .
课堂小结
1.解二元一次方程组的思想方法:通过代入的方法,
达到消元的目的,化二元一次方程组为一元一次
方程求解.
2.用代入消元法解二元一次方程组的基本步骤:
(1)从方程组中选取一个未知数系数比较简单的方程;
(2)用一个未知数的代数式表示另一个未知数;
(3)把代数式代入到另一个方程,得到一个一元一次方程;
(4)解一元一次方程,求出未知数的值;
(5)把未知数的值代入代数式,求出另一个未知数的值;
(6)写出方程组的解.
作业与课外学习任务
1.练习作业:学习检测P26-28 第1至22题
书面课本P36 习题7.2 1(1)(2)
2.课外学习任务:
预习课本P29 7.2 二元一次方程组的解法 例2
教学反馈:
作业存在的主要问题:
随堂练习
①
②
解:①×3 + ②×2得:
13x=52.
∴ x=4.
将x=4代入②,得:
8+3y=17.
∴ y=3.
①
②
解: ① +②× 2 得:
14x=28.
∴ x=2.
将x=2代入②,得:
10+y=7.
∴ y=-3.
随堂练习
①
②
解:①×7 + ②×3得:
16x=160.
∴ x=10.
将x=10代入②,得:
30+7y=100.
∴ y=10.
①
②
解: ①×5 +②× 3 得:
-11x=55.
∴ x= -5.
将x= - 5代入②,得:
10+y=7.
∴ y=-3.
随堂练习
①
②
解:①×3 + ②×2得:
13x=52.
∴ x=4.
将x=4代入②,得:
8+3y=17.
∴ y=3.
①
②
解: ① +②× 2 得:
14x=28.
∴ x=2.
将x=2代入②,得:
10+y=7.
∴ y=-3.
随堂练习
①
②
解:①×7 + ②×3得:
16x=160.
∴ x=10.
将x=10代入②,得:
30+7y=100.
∴ y=10.
①
②
解: ①×5 +②× 3 得:
-11x=55.
∴ x= -5.
将x= - 5代入②,得:
5y+35=5.
∴ y=-6.
随堂练习
①
②
解:①×3 + ②×2得:
13x=52.
∴ x=4.
将x=4代入②,得:
8+3y=17.
∴ y=3.
①
②
解: ① +②× 2 得:
14x=28.
∴ x=2.
将x=2代入②,得:
10+y=7.
∴ y=-3.
随堂练习
①
②
解:①×7 + ②×3得:
16x=160.
∴ x=10.
将x=10代入②,得:
30+7y=100.
∴ y=10.
①
②
解: ①×5 +②× 3 得:
-11x=55.
∴ x= -5.
将x= - 5代入②,得:
5y+35=5.
∴ y=-6.
用加减消元法解二元一次方程组的基本步骤:
(1)把一个方程或两个方程的两边同乘以适当的数,使两个方程中的某一个未知数的系数的绝对值相等;
(2)把所得的两个方程的两边分别相加或相减,
消去一个未知数,得到一个一元一次方程;
(3)解这个方程,求得一个未知数的值;
(4)把所求得的未知数的值代入方程组中某一个
方程,求出另一个未知数的值;
(5)把求得的未知数的值写成 的形式.
课堂小结
作业与课外学习任务
1.练习作业:学习检测P26-28 第1至22题
书面课本P36 习题7.2 1(3)(4)
2.课外学习任务:
预习课本P34 7.2 二元一次方程组的解法 例6
例2 解下列方程组:
①
②
解:① + ②得:
7x=14.
∴ x=2.
将x=2代入①,得:
3×2+7y=9.
解得:
解: ② - ①得:
①
②
7y=-14.
∴ y=-2.
将y=-2代入①,得:
2x-5×(-2)=9.
解得:
哪一个未知数的系数相同或相反?
随堂练习
①
②
解:①×3 + ②×2得:
13x=52.
∴ x=4.
将x=4代入②,得:
8+3y=17.
∴ y=3.
①
②
解: ① +②× 2 得:
14x=28.
∴ x=2.
将x=2代入②,得:
10+y=7.
∴ y=-3.
随堂练习
①
②
解:①×7 + ②×3得:
16x=160.
∴ x=10.
将x=10代入②,得:
30+7y=100.
∴ y=10.
①
②
解: ①×5 +②× 3 得:
-11x=55.
∴ x= -5.
将x= - 5代入②,得:
5y+35=5.
∴ y=-6.
7.2 二元一次方程组的解法
2.加减消元法
教学目标
教学重点与难点
重点:理解并掌握加减消元法解二元一次方程组.
难点:理解解方程组的基本思想是“消元”,会化二元
一次方程组为一元一次方程.
1.使学生通过探索,逐步发现解方程的基本思想
是“消元”,化二元一次方程组为一元一次方程.
2.使学生了解“加减消元法”,并掌握加减消元法解二元一次方程组.
3.通过加减消元,使学生进一步理解把“未知”转化
为“已知”,和复杂问题转化为简单问题思想方法.
温故夯基
一.代入消元法解二元一次方程组的基本步骤:
(1)从方程组中选取一个未知数系数比较简单的方程;
(2)用一个未知数的代数式表示另一个未知数;
(3)把代数式代入到另一个方程,得到一个一元一次方程;
(4)解一元一次方程,求出未知数的值;
(5)把未知数的值代入代数式,求出另一个未知数的值;
(6)写出方程组的解.
二.用代入法解二元一次方程组的两种类型:
1.未知数的系数含1或-1的方程组;
2.未知数的系数不含1或-1的方程组.
巩固练习
1.解下列方程组:
解:由① 得:x=-2y.
①
②
③
将 ③代入 ②,得:
3(-2y)+4y=6.
解得:y=-3.
将y=-3代入③,得:x=6.
①
②
解:由① 得:x=
③
将 ③代入 ②,得:
解得:y=-1.
将y=-1代入③,得:x=7.
学习新知
怎么解下面的二元一次方程组?
方法引入
还有其他的解法吗?
方程组的各个未知数的系数有什么特点?
两个方程相加,行吗?
两个方程相减,行吗?
例题精析
例1 解下列方程组:
①
②
解:① + ②得:
5x=15.
∴ x=3.
将x=3代入①,得:
2×3+5y=8.
解得:
解:① - ②得:
①
②
9y=-18.
∴ y=-2.
将y=-2代入①,得:
3x+5×(-2)=5.
解得:
x=5.
两个二元一次方程中同一个未知数的系数相同或
相反时,将两个方程两边分别相减或相加就能消去
这个未知数,得到一个一元一次方程,这种方法
叫做加减消元法,简称加减法.
加减消元法
方法总结
例2 解下列方程组:
①
②
解:① + ②得:
7x=14.
∴ x=2.
将x=2代入①,得:
3×2+7y=9.
解得:
解: ② - ①得:
①
②
7y=-14.
∴ y=-2.
将y=-2代入①,得:
2x-5×(-2)=9.
解得:
随堂练习
①
②
解:① + ②得:
8x=8.
∴ x=1.
将x=1代入①,得:
5×1+y=7.
∴ y=2.
①
②
解: ② - ①得:
9y=9.
∴ y=1.
将y=1代入①,得:
4x-3×1=5.
∴ x=2.
解:① - ②得:
①
②
14y=-14.
∴ y=-1.
将y=-1代入①,得:
6x+7×(-1)=5.
∴ x=2.
①
②
解:① + ②得:
2y=2.
∴ y=1.
将y=1代入①,得:
0.5x-3×1=-1.
∴ x=4.
解:① - ②得:
①
②
5y=10.
∴ y=2.
将y=2代入①,得:
5x+3×2=6.
∴ x=0.
①
②
解:① + ②得:
4x=4.
∴ x=1.
将x=1代入①,得:
1+2y=9.
∴ y=4.
例3 已知 是关于x,y的二元一次方程组
的一组解,求a+b的值.
解:
解方程组得:
∴ a+b=2+3=5.
已知关于x,y的二元一次方程组
的解为 ,求a-2b的值.
解:
解方程组得:
∴ a-2b=
随堂练习
=2.
学习新知
例4 解方程组:
直接相加或相加
能否消去未知数?
①
②
能不能化为未知数
相同或相反的类型?
最小公倍数
解:①×3 + ②×2得:
19x=114.
∴ x=6.
将x=6代入②,得:
30+6y=42.
∴ y=2.
能否先消去x再求解?
怎么做?
学习新知
例4 解方程组:
①
②
最小公倍数
解: ②×3 - ①×5得:
38y=76.
∴ y=2.
将y=2代入②,得:
5x+12=42.
∴ x=6.
用加减消元法解二元一次方程组的基本步骤:
方法总结
(1)把一个方程或两个方程的两边同乘以适当的数,使两个方程中的某一个未知数的系数的绝对值相等;
(2)把所得的两个方程的两边分别相加或相减,
消去一个未知数,得到一个一元一次方程;
(3)解这个方程,求得一个未知数的值;
(4)把所求得的未知数的值代入方程组中某一个
方程,求出另一个未知数的值;
(5)把求得的未知数的值写成 的形式.
例题精析
例5 解方程组:
①
②
37x=111.
∴ x=3.
将x=3代入②,得:
21+4y=-15.
∴ y=-9.
解:①×4 + ②×3得:
随堂练习
①
②
解:①×3 + ②×2得:
13x=52.
∴ x=4.
将x=4代入②,得:
8+3y=17.
∴ y=3.
①
②
解: ① +②× 2 得:
14x=28.
∴ x=2.
将x=2代入②,得:
10+y=7.
∴ y=-3.
随堂练习
①
②
解:①×7 + ②×3得:
16x=160.
∴ x=10.
将x=10代入②,得:
30+7y=100.
∴ y=10.
①
②
解: ① +②× 2 得:
14x=28.
∴ x=2.
将x=2代入②,得:
10+y=7.
∴ y=-3.
随堂练习
解下列方程组:
①
②
解:将① 代入②,得:
(3y+2)+3y=8,
解得:
y=1.
将y=1代入①,得:
x=5.
解:将② 代入①,得:
①
②
4x-3(7-5x)=17,
解得:
x=2.
将x=2代入②,得:
y= - 3.
①
②
解:由①得:
x=y-5 . ③
将③ 代入②,得:
3(y-5)+2y=10,
解得:
y=5.
将y=5代入③,得:
x=0.
①
②
解:由②得:
y=2x-3.2 . ③
将③ 代入①,得:
2x-7(2x-3.2)=8,
解得:
x=1.2 .
将x=1.2代入③,得:
y=-0.8 .
课堂小结
1.解二元一次方程组的思想方法:通过代入的方法,
达到消元的目的,化二元一次方程组为一元一次
方程求解.
2.用代入消元法解二元一次方程组的基本步骤:
(1)从方程组中选取一个未知数系数比较简单的方程;
(2)用一个未知数的代数式表示另一个未知数;
(3)把代数式代入到另一个方程,得到一个一元一次方程;
(4)解一元一次方程,求出未知数的值;
(5)把未知数的值代入代数式,求出另一个未知数的值;
(6)写出方程组的解.
作业与课外学习任务
1.练习作业:学习检测P26-28 第1至22题
书面课本P36 习题7.2 1(1)(2)
2.课外学习任务:
预习课本P29 7.2 二元一次方程组的解法 例2
教学反馈:
作业存在的主要问题:
随堂练习
①
②
解:①×3 + ②×2得:
13x=52.
∴ x=4.
将x=4代入②,得:
8+3y=17.
∴ y=3.
①
②
解: ① +②× 2 得:
14x=28.
∴ x=2.
将x=2代入②,得:
10+y=7.
∴ y=-3.
随堂练习
①
②
解:①×7 + ②×3得:
16x=160.
∴ x=10.
将x=10代入②,得:
30+7y=100.
∴ y=10.
①
②
解: ①×5 +②× 3 得:
-11x=55.
∴ x= -5.
将x= - 5代入②,得:
10+y=7.
∴ y=-3.
随堂练习
①
②
解:①×3 + ②×2得:
13x=52.
∴ x=4.
将x=4代入②,得:
8+3y=17.
∴ y=3.
①
②
解: ① +②× 2 得:
14x=28.
∴ x=2.
将x=2代入②,得:
10+y=7.
∴ y=-3.
随堂练习
①
②
解:①×7 + ②×3得:
16x=160.
∴ x=10.
将x=10代入②,得:
30+7y=100.
∴ y=10.
①
②
解: ①×5 +②× 3 得:
-11x=55.
∴ x= -5.
将x= - 5代入②,得:
5y+35=5.
∴ y=-6.
随堂练习
①
②
解:①×3 + ②×2得:
13x=52.
∴ x=4.
将x=4代入②,得:
8+3y=17.
∴ y=3.
①
②
解: ① +②× 2 得:
14x=28.
∴ x=2.
将x=2代入②,得:
10+y=7.
∴ y=-3.
随堂练习
①
②
解:①×7 + ②×3得:
16x=160.
∴ x=10.
将x=10代入②,得:
30+7y=100.
∴ y=10.
①
②
解: ①×5 +②× 3 得:
-11x=55.
∴ x= -5.
将x= - 5代入②,得:
5y+35=5.
∴ y=-6.
用加减消元法解二元一次方程组的基本步骤:
(1)把一个方程或两个方程的两边同乘以适当的数,使两个方程中的某一个未知数的系数的绝对值相等;
(2)把所得的两个方程的两边分别相加或相减,
消去一个未知数,得到一个一元一次方程;
(3)解这个方程,求得一个未知数的值;
(4)把所求得的未知数的值代入方程组中某一个
方程,求出另一个未知数的值;
(5)把求得的未知数的值写成 的形式.
课堂小结
作业与课外学习任务
1.练习作业:学习检测P26-28 第1至22题
书面课本P36 习题7.2 1(3)(4)
2.课外学习任务:
预习课本P34 7.2 二元一次方程组的解法 例6
例2 解下列方程组:
①
②
解:① + ②得:
7x=14.
∴ x=2.
将x=2代入①,得:
3×2+7y=9.
解得:
解: ② - ①得:
①
②
7y=-14.
∴ y=-2.
将y=-2代入①,得:
2x-5×(-2)=9.
解得:
哪一个未知数的系数相同或相反?
随堂练习
①
②
解:①×3 + ②×2得:
13x=52.
∴ x=4.
将x=4代入②,得:
8+3y=17.
∴ y=3.
①
②
解: ① +②× 2 得:
14x=28.
∴ x=2.
将x=2代入②,得:
10+y=7.
∴ y=-3.
随堂练习
①
②
解:①×7 + ②×3得:
16x=160.
∴ x=10.
将x=10代入②,得:
30+7y=100.
∴ y=10.
①
②
解: ①×5 +②× 3 得:
-11x=55.
∴ x= -5.
将x= - 5代入②,得:
5y+35=5.
∴ y=-6.
