华东师大版七年级下册数学课件:9.1.2 三角形的内角和与外角和(共23张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学课件:9.1.2 三角形的内角和与外角和(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 17:32:39 | ||
图片预览



文档简介
第9章 多 边 形
9.1 三 角 形
2.三角形的内角和与外角和
教学目标
教学重点与难点
重点:三角形的内角和与外角和,三角形的外角的两条性质及应用.
难点:三角形的外角的两条性质及其应用.
1. 理解和掌握三角形的内角和等于180o并会应用.
2.理解和掌握三角形的外角和等于360o并会应用.
3.理解和掌握三角形的外角的两条性质及其应用.
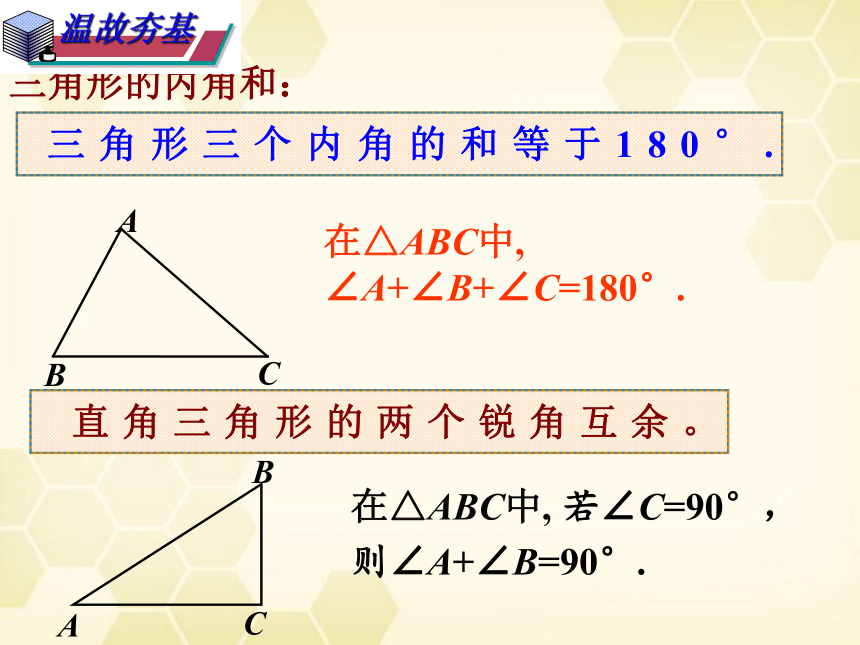
三角形的内角和:
三角形三个内角的和等于180°.
C
B
A
在△ABC中, ∠A+∠B+∠C=180°.
直角三角形的两个锐角互余。
B
A
C
在△ABC中, 若∠C=90°,
则∠A+∠B=90°.
温故夯基
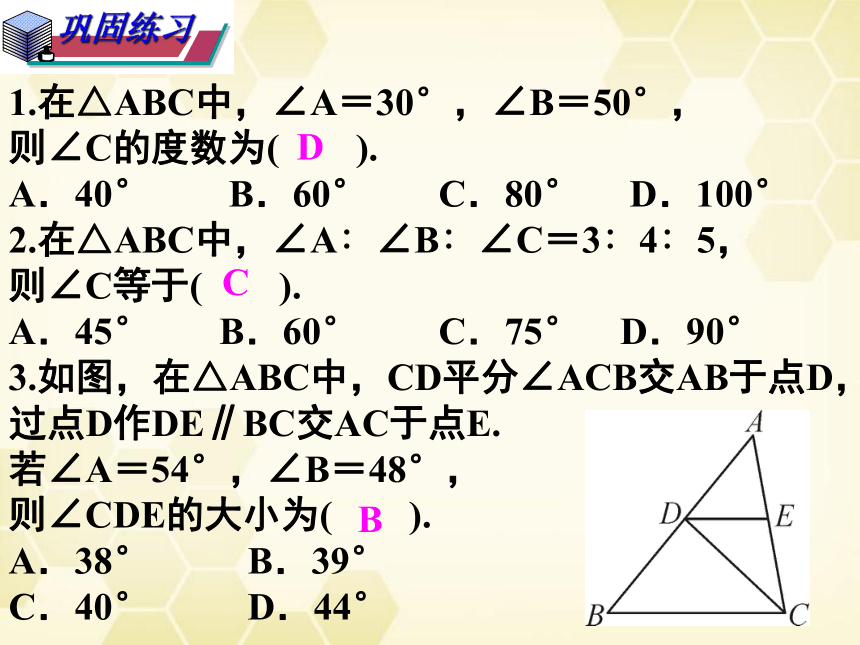
1.在△ABC中,∠A=30°,∠B=50°,
则∠C的度数为( ).
A.40° B.60° C.80° D.100°
2.在△ABC中,∠A∶∠B∶∠C=3∶4∶5,
则∠C等于( ).
A.45° B.60° C.75° D.90°
3.如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.
若∠A=54°,∠B=48°,
则∠CDE的大小为( ).
A.38° B.39°
C.40° D.44°
D
C
巩固练习
B
4.已知a∥b,某学生将一直角三角板放置如图所示,如果∠1=35°,那么∠2的度数为( ).
A.35° B.55° C.56° D.65°
5.如图,在△ABC中,∠C=90°,∠B=40°.
若AD是角平分线,则∠ADC的度数为 ( ).
A.25° B.50° C.65° D.70°
(第4题图)
(第5题图)
B
C
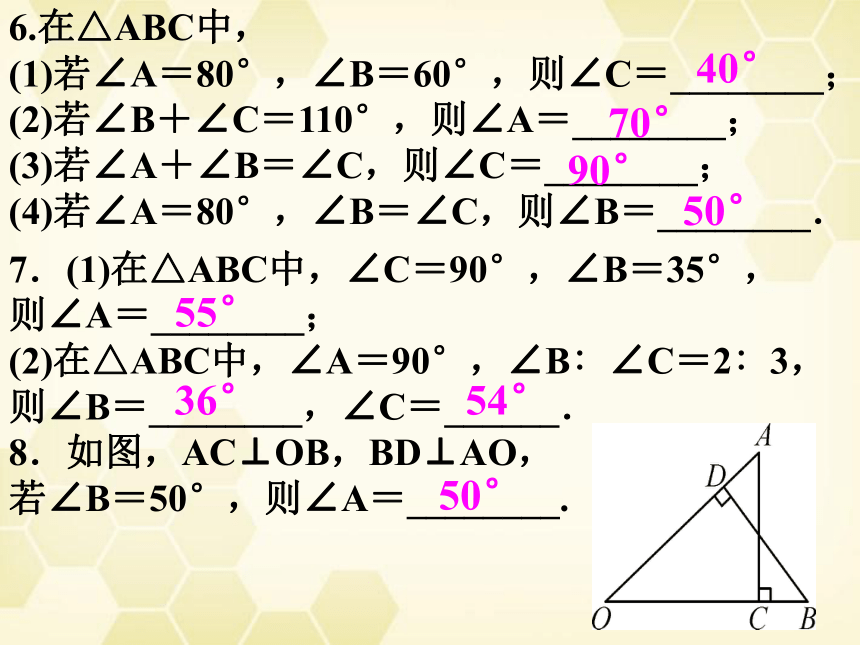
6.在△ABC中,
(1)若∠A=80°,∠B=60°,则∠C=________;
(2)若∠B+∠C=110°,则∠A=________;
(3)若∠A+∠B=∠C,则∠C=________;
(4)若∠A=80°,∠B=∠C,则∠B=________.
7.(1)在△ABC中,∠C=90°,∠B=35°,
则∠A=________;
(2)在△ABC中,∠A=90°,∠B∶∠C=2∶3,
则∠B=________,∠C=______.
8.如图,AC⊥OB,BD⊥AO,
若∠B=50°,则∠A=________.
40°
70°
90°
50°
55°
36°
54°
50°
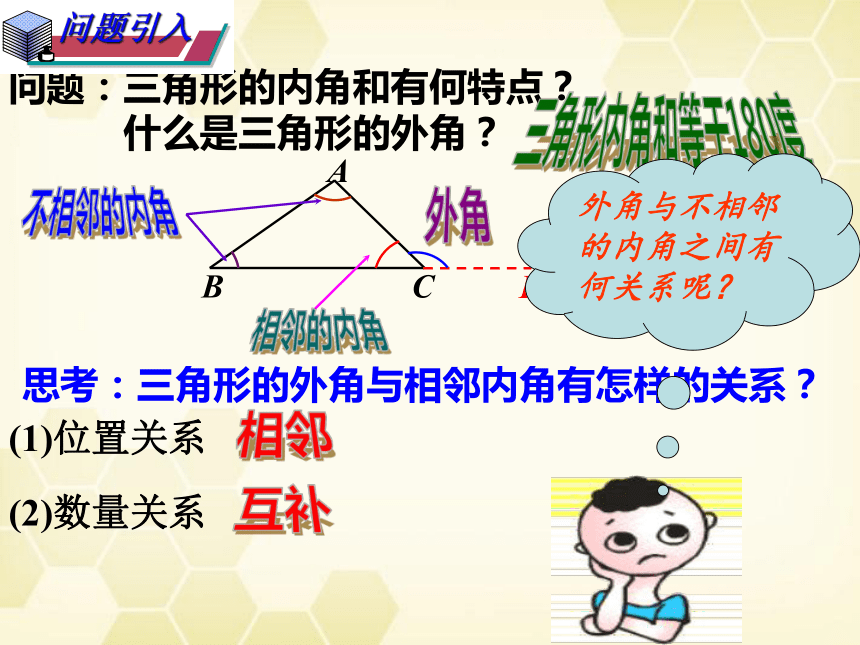
问题:三角形的内角和有何特点?
什么是三角形的外角?
B
C
A
思考:三角形的外角与相邻内角有怎样的关系?
D
(1)位置关系
(2)数量关系
外角与不相邻的内角之间有何关系呢?
问题引入
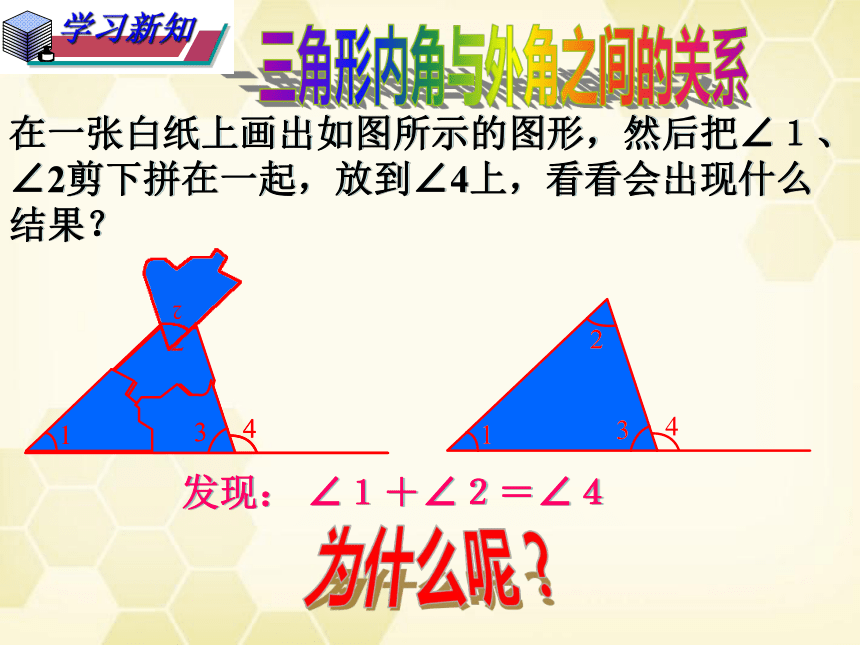
在一张白纸上画出如图所示的图形,然后把∠1、∠2剪下拼在一起,放到∠4上,看看会出现什么结果?
发现: ∠1+∠2=∠4
学习新知
B
D
A
C
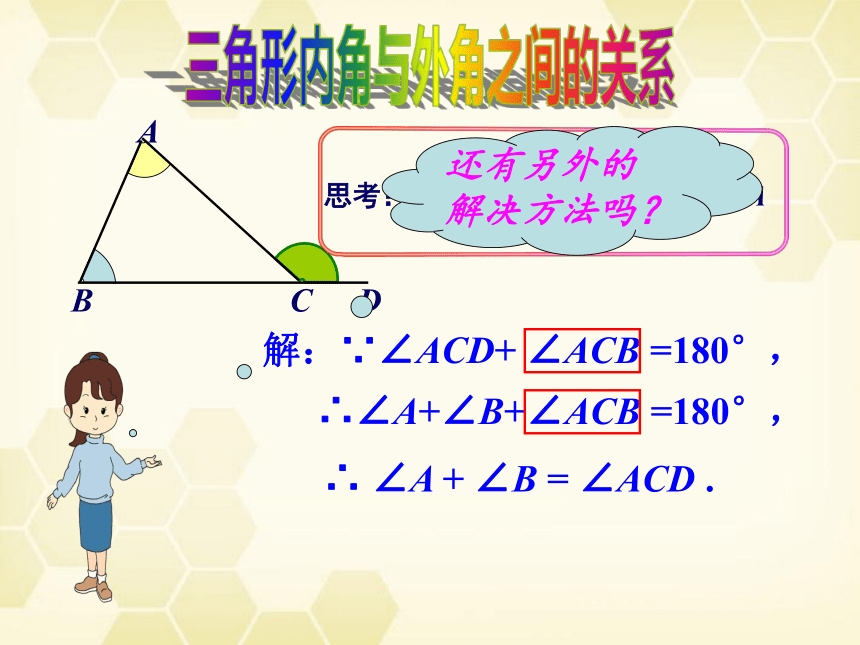
思考:如何说明∠ACD= ∠B+ ∠A
∴∠A+∠B+∠ACB =180°,
解:∵∠ACD+ ∠ACB =180°,
∴ ∠A + ∠B = ∠ACD .
还有另外的
解决方法吗?
B
D
A
C
1
2
E
解:过C作CE∥AB,
∴∠1= ∠B,
∠2=∠A,
∴∠1+ ∠2= ∠A+ ∠B,
即∠ACD= ∠A+ ∠B .
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角与任何一个与它不相邻的内角之间有什么关系呢?
B
D
A
C
∵∠A+∠B=∠ACD,
∴ ∠ACD>∠ A,
∠ACD>∠ B .
三角形的一个外角大于任何一个与它不相邻的
内角.
三角形的一个外角与任何一个与它不相邻的内角之间有什么大小关系呢?
外角与相邻内角
B
D
A
C
外角与相邻的内角互补.
∠ACD+∠ACB=180°.
外角与不相邻内角
∠A+∠B=∠ACD.
∠ACD>∠ A,
∠ACD>∠ B.
归纳总结
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于任何一个与它不相邻的内角.
30°
60°
1
120°
1
35°
50°
45°
1
例题精析
例1 (1)求下列图中∠1的度数:
(2)如图所示:
则∠1=_____;∠2=_____; ∠3=______.
2
125°
40°
3
1
2.如图所示,判断∠1与∠3的大小,并说明理由.
3
2
1
C
B
A
D
E
∵∠3 >∠2 ,∠2 >∠1,
解:∠3 >∠1.
理由如下:
∴ ∠3 >∠1.
随堂练习
1.如图:∠1=25°,∠2=95°,∠3=30°,
则∠4=_____.
A
D
E
C
B
1
4
3
2
D
E
F
A
B
1
2
3
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和。
如图:∠1+ ∠2+ ∠3就是△ABC的外角和.
思考: ∠1+ ∠2+ ∠3= ?度
学习新知
C
F
做一做
∠1+ =180°,
∠2+ =180°,
∠3+ =180°.
∠BAC
∠ABC
∠ACB
把三个等式左右两边分别相加可以得到:
∠1+∠2+∠3+∠BAC+∠ABC+∠ACB = ,(1)
而∠BAC+∠ABC+∠ACB=180°,(2)
比较(1)、(2),你能得出什么结论?
∠1+∠2+∠3=360°.
三角形的外角和等于360°.
D
E
F
A
B
1
2
3
C
F
A
B
D
C
解:(1)∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=80? .
又∵∠B=∠BAD,
∴∠B=40? .
(2)∵∠B+∠BAC+∠C= 180?,
∴ ∠C=180? -∠B-∠BAC
=180? -40? -70?
=70?.
例题精析
例2 如图,D是△ABC的BC边上一点,∠B=∠BAD,
∠ADC=80? ,∠BAC=70?.求:
(1)∠B的度数;(2)∠C的度数.
E
D
C
B
A
1
2
解:∵∠1= ∠B+ ∠D,
又∵∠2= ∠C+ ∠E,
∴ ∠A+∠B+∠C+∠D+∠E
=(∠B+ ∠D)+(∠C+ ∠E)+∠A
=∠1+∠2+∠A
=180°.
例3 如图所示,求∠A+∠B+∠C+∠D+∠E的度数.
例题精析
随堂练习
1.三角形三个外角之比为2:3:4,则与它们相邻的
内角为( ).
A. 80? , 120? , 160 ? B. 160 ? , 120 ? , 80 ?
C. 100 ? , 60 ? ,20 ? D. 140 ? , 120 ? , 100 ?
C
2.如图所示,则∠A+∠B+∠C+∠D+∠E+∠F= .
D
E
F
C
B
A
1
2
3
M
N
P
∠1= ,
∠2= ,
∠3= ,
∠E+∠F
∠A+∠B
∠C+∠D
=∠1+∠2+∠3
A
B
O
C
D
解:延长BO交AC于点D,
∴ ∠BOC = ∠A + ∠B+∠C
= 60°+30°+40°
∴ ∠BDC = ∠A + ∠B,
∠BOC = ∠BDC +∠C,
=130°.
A
B
O
C
A
B
O
C
1
2
3
4
1
2
3.如图,∠A=60°,∠B=30°,∠C=40°,求∠BOC .
你还有另外的解法吗?
课堂小结
一. 三角形的外角的两条性质:
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于任何一个与它不相邻的内角.
二. 三角形的外角和:
三角形的外角和等于360°.
作业与课外学习任务
1.练习作业:学习检测P56-57 第1至12题
书面作业课本P82 习题9.1 3,4
2.课外学习任务:
预习P80 9.1.3 三角形的三边关系
教学反馈:
作业存在的主要问题:
9.1 三 角 形
2.三角形的内角和与外角和
教学目标
教学重点与难点
重点:三角形的内角和与外角和,三角形的外角的两条性质及应用.
难点:三角形的外角的两条性质及其应用.
1. 理解和掌握三角形的内角和等于180o并会应用.
2.理解和掌握三角形的外角和等于360o并会应用.
3.理解和掌握三角形的外角的两条性质及其应用.
三角形的内角和:
三角形三个内角的和等于180°.
C
B
A
在△ABC中, ∠A+∠B+∠C=180°.
直角三角形的两个锐角互余。
B
A
C
在△ABC中, 若∠C=90°,
则∠A+∠B=90°.
温故夯基
1.在△ABC中,∠A=30°,∠B=50°,
则∠C的度数为( ).
A.40° B.60° C.80° D.100°
2.在△ABC中,∠A∶∠B∶∠C=3∶4∶5,
则∠C等于( ).
A.45° B.60° C.75° D.90°
3.如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.
若∠A=54°,∠B=48°,
则∠CDE的大小为( ).
A.38° B.39°
C.40° D.44°
D
C
巩固练习
B
4.已知a∥b,某学生将一直角三角板放置如图所示,如果∠1=35°,那么∠2的度数为( ).
A.35° B.55° C.56° D.65°
5.如图,在△ABC中,∠C=90°,∠B=40°.
若AD是角平分线,则∠ADC的度数为 ( ).
A.25° B.50° C.65° D.70°
(第4题图)
(第5题图)
B
C
6.在△ABC中,
(1)若∠A=80°,∠B=60°,则∠C=________;
(2)若∠B+∠C=110°,则∠A=________;
(3)若∠A+∠B=∠C,则∠C=________;
(4)若∠A=80°,∠B=∠C,则∠B=________.
7.(1)在△ABC中,∠C=90°,∠B=35°,
则∠A=________;
(2)在△ABC中,∠A=90°,∠B∶∠C=2∶3,
则∠B=________,∠C=______.
8.如图,AC⊥OB,BD⊥AO,
若∠B=50°,则∠A=________.
40°
70°
90°
50°
55°
36°
54°
50°
问题:三角形的内角和有何特点?
什么是三角形的外角?
B
C
A
思考:三角形的外角与相邻内角有怎样的关系?
D
(1)位置关系
(2)数量关系
外角与不相邻的内角之间有何关系呢?
问题引入
在一张白纸上画出如图所示的图形,然后把∠1、∠2剪下拼在一起,放到∠4上,看看会出现什么结果?
发现: ∠1+∠2=∠4
学习新知
B
D
A
C
思考:如何说明∠ACD= ∠B+ ∠A
∴∠A+∠B+∠ACB =180°,
解:∵∠ACD+ ∠ACB =180°,
∴ ∠A + ∠B = ∠ACD .
还有另外的
解决方法吗?
B
D
A
C
1
2
E
解:过C作CE∥AB,
∴∠1= ∠B,
∠2=∠A,
∴∠1+ ∠2= ∠A+ ∠B,
即∠ACD= ∠A+ ∠B .
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角与任何一个与它不相邻的内角之间有什么关系呢?
B
D
A
C
∵∠A+∠B=∠ACD,
∴ ∠ACD>∠ A,
∠ACD>∠ B .
三角形的一个外角大于任何一个与它不相邻的
内角.
三角形的一个外角与任何一个与它不相邻的内角之间有什么大小关系呢?
外角与相邻内角
B
D
A
C
外角与相邻的内角互补.
∠ACD+∠ACB=180°.
外角与不相邻内角
∠A+∠B=∠ACD.
∠ACD>∠ A,
∠ACD>∠ B.
归纳总结
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于任何一个与它不相邻的内角.
30°
60°
1
120°
1
35°
50°
45°
1
例题精析
例1 (1)求下列图中∠1的度数:
(2)如图所示:
则∠1=_____;∠2=_____; ∠3=______.
2
125°
40°
3
1
2.如图所示,判断∠1与∠3的大小,并说明理由.
3
2
1
C
B
A
D
E
∵∠3 >∠2 ,∠2 >∠1,
解:∠3 >∠1.
理由如下:
∴ ∠3 >∠1.
随堂练习
1.如图:∠1=25°,∠2=95°,∠3=30°,
则∠4=_____.
A
D
E
C
B
1
4
3
2
D
E
F
A
B
1
2
3
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和。
如图:∠1+ ∠2+ ∠3就是△ABC的外角和.
思考: ∠1+ ∠2+ ∠3= ?度
学习新知
C
F
做一做
∠1+ =180°,
∠2+ =180°,
∠3+ =180°.
∠BAC
∠ABC
∠ACB
把三个等式左右两边分别相加可以得到:
∠1+∠2+∠3+∠BAC+∠ABC+∠ACB = ,(1)
而∠BAC+∠ABC+∠ACB=180°,(2)
比较(1)、(2),你能得出什么结论?
∠1+∠2+∠3=360°.
三角形的外角和等于360°.
D
E
F
A
B
1
2
3
C
F
A
B
D
C
解:(1)∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=80? .
又∵∠B=∠BAD,
∴∠B=40? .
(2)∵∠B+∠BAC+∠C= 180?,
∴ ∠C=180? -∠B-∠BAC
=180? -40? -70?
=70?.
例题精析
例2 如图,D是△ABC的BC边上一点,∠B=∠BAD,
∠ADC=80? ,∠BAC=70?.求:
(1)∠B的度数;(2)∠C的度数.
E
D
C
B
A
1
2
解:∵∠1= ∠B+ ∠D,
又∵∠2= ∠C+ ∠E,
∴ ∠A+∠B+∠C+∠D+∠E
=(∠B+ ∠D)+(∠C+ ∠E)+∠A
=∠1+∠2+∠A
=180°.
例3 如图所示,求∠A+∠B+∠C+∠D+∠E的度数.
例题精析
随堂练习
1.三角形三个外角之比为2:3:4,则与它们相邻的
内角为( ).
A. 80? , 120? , 160 ? B. 160 ? , 120 ? , 80 ?
C. 100 ? , 60 ? ,20 ? D. 140 ? , 120 ? , 100 ?
C
2.如图所示,则∠A+∠B+∠C+∠D+∠E+∠F= .
D
E
F
C
B
A
1
2
3
M
N
P
∠1= ,
∠2= ,
∠3= ,
∠E+∠F
∠A+∠B
∠C+∠D
=∠1+∠2+∠3
A
B
O
C
D
解:延长BO交AC于点D,
∴ ∠BOC = ∠A + ∠B+∠C
= 60°+30°+40°
∴ ∠BDC = ∠A + ∠B,
∠BOC = ∠BDC +∠C,
=130°.
A
B
O
C
A
B
O
C
1
2
3
4
1
2
3.如图,∠A=60°,∠B=30°,∠C=40°,求∠BOC .
你还有另外的解法吗?
课堂小结
一. 三角形的外角的两条性质:
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于任何一个与它不相邻的内角.
二. 三角形的外角和:
三角形的外角和等于360°.
作业与课外学习任务
1.练习作业:学习检测P56-57 第1至12题
书面作业课本P82 习题9.1 3,4
2.课外学习任务:
预习P80 9.1.3 三角形的三边关系
教学反馈:
作业存在的主要问题:
