华东师大版七年级下册数学课件:9.1.2 三角形的内角和与外角和(共27张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学课件:9.1.2 三角形的内角和与外角和(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 17:34:16 | ||
图片预览






文档简介
第9章 多 边 形
9.1 三 角 形
2.三角形的内角和与外角和
教学目标
教学重点与难点
重点:三角形的内角和与外角和,三角形的外角的两条性质及应用.
难点:三角形的外角的两条性质及其应用.
1. 理解和掌握三角形的内角和等于180o并会应用.
2.理解和掌握三角形的外角和等于360o并会应用.
3.理解和掌握三角形的外角的两条性质及其应用.
O
A
B
C
D
E
F
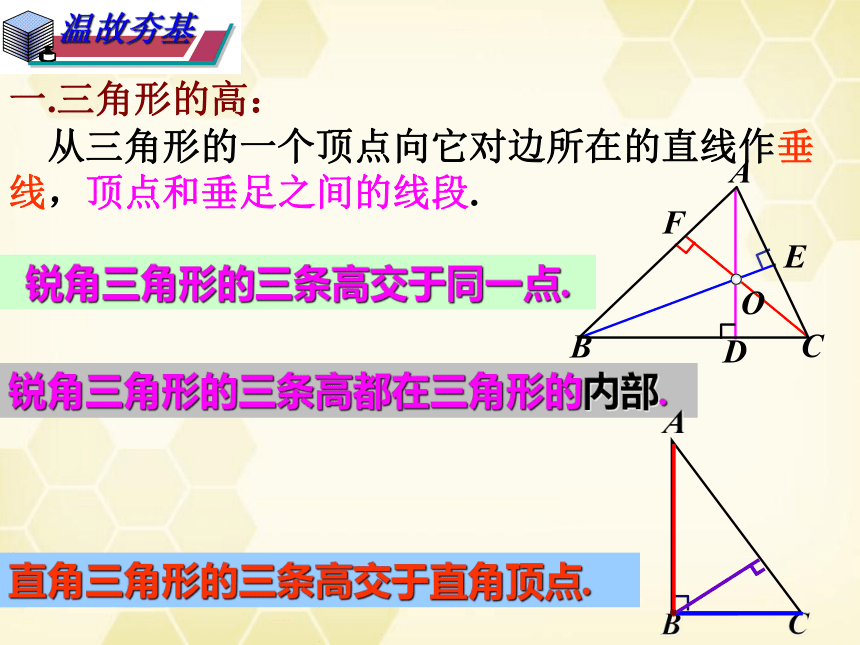
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
温故夯基
一.三角形的高:
从三角形的一个顶点向它对边所在的直线作垂线,顶点和垂足之间的线段.
A
B
C
●
直角三角形的三条高交于直角顶点.
A
B
C
D
E
F
钝角三角形的三条高不相交于一点.
钝角三角形的三条高
所在直线交于一点
三角形的三条高所在直线交于一点
A
B
C
D
●
●
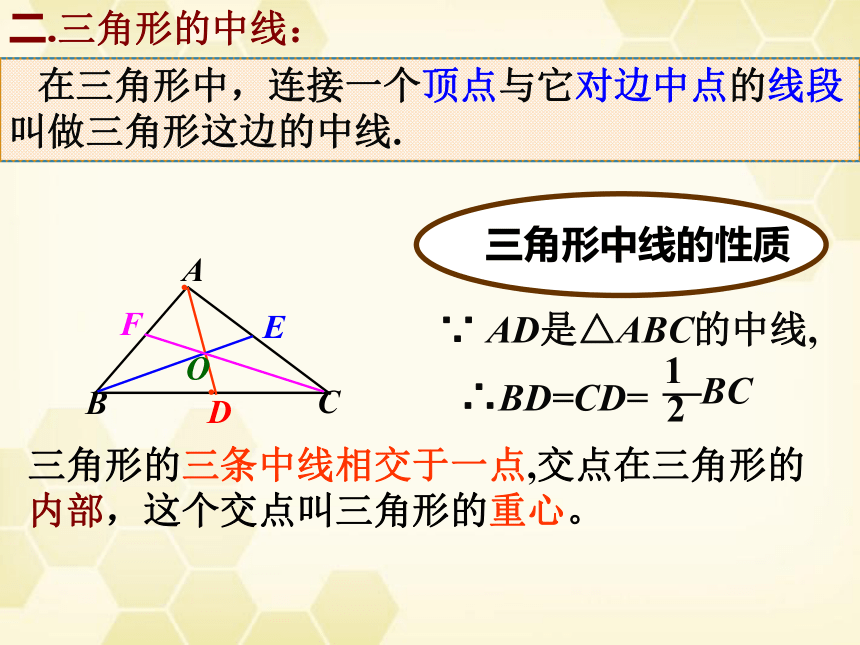
在三角形中,连接一个顶点与它对边中点的线段叫做三角形这边的中线.
∵ AD是△ABC的中线,
∴BD=CD=
1
2
BC
E
F
O
三角形中线的性质
二.三角形的中线:
三角形的三条中线相交于一点,交点在三角形的
内部,这个交点叫三角形的重心。
A
B
C
D
●
●
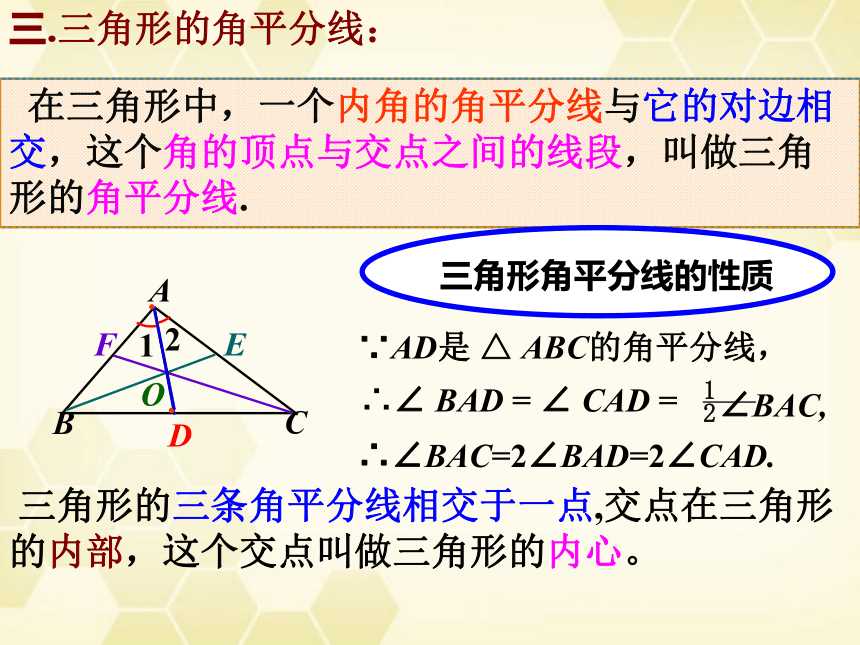
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
E
F
O
1
2
∵AD是 △ ABC的角平分线,
∴∠ BAD = ∠ CAD =
1
2
∠BAC,
∴∠BAC=2∠BAD=2∠CAD.
三角形角平分线的性质
三.三角形的角平分线:
三角形的三条角平分线相交于一点,交点在三角形
的内部,这个交点叫做三角形的内心。
巩固练习
1.如果一个三角形的三条高的交点恰是这个三角形
的一个顶点,那么这个三角形是( ).
A.锐角三角形 B.钝角三角形
C.直角三角形 D.等边三角形
C
2.下列线段一定在三角形内部的是( ).
①三角形的三条中线;②三角形的三条高;
③三角形的三条角平分线.
A.①② B.①③ C.②③ D.①②③
B
3.下列说法:
①三角形的角平分线、中线、高都是线段;
②直角三角形只有一条高;
③若一个三角形的三条高都在三角形的内部,
则这个三角形一定是锐角三角形;
④若一个三角形有两条高在三角形的外部,
则这个三角形一定是钝角三角形.
其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
√
×
√
√
C
4.如图,AE⊥BC,BF⊥AC,CD⊥AB,
垂足分别为E,F,D,则△ABC中,
AC边上的高是线段( ).
A.AE B.CD
C.AF D.BF
D
5.如图,AD是△ABC的中线.
(1)若AB=4,AD=3,BC=6,
则△ABD的周长为________;
(2)若AB=4,且△ABD和△ACD的周长之差为1,
则AC=________.
10
3或5
在纸片上画任意的三角形△ABC(把表示三角形三个顶点的字母标在三角形的内部)动手操作剪下内角拼一拼,你能得到什么结论?
A
B
C
问题引入
思考:锐角三角形、直角三角形、钝角三角形的内角和有什么共同特点?
共同特点:三角形的内角和等于180。.
在纸片上画任意的三角形△ABC(把表示三角形三个顶点的字母标在三角形的内部)动手操作剪下内角拼一拼,你能得到什么结论?
A
B
C
B
C
C
A
B
A
B
三角形三个内角的和等于180°.
同学们观察和总结的非常棒,但这只是实验,而观察与实验得到的结论不一定正确,可靠,这样就需要通过数学证明来验证结论是否正确.
从刚才拼角的过程你能想出证明的办法吗?
探究发现
这是一个文字命题,如何转化为几何命题,
结合图形,你能写出已知和求证吗?
C
B
A
求证:∠A+∠B+∠C=180°.
已知:△ABC.
A
C
B
C
B
F
1
E
证明:过点A作EF∥BC ,
∴∠B=∠1,∠C=∠2.
(两直线平行,内错角相等)
∵∠1+∠3+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。
在平面几何里,辅助线通常画成虚线。
三角形三个内角的和等于180°
2
推理论证
三角形三个内角的和等于180°
C
B
A
D
E
1
2
推理论证
已知:△ABC.
求证:∠A+∠B+∠C=180°.
证明:延长BC至点E,过点C作CD∥BA .
∴∠B=∠1,
∠A=∠2.
(两直线平行,同位角相等)
(两直线平行,内错角相等)
∵∠1+∠2+∠BCA=180°,
∴∠A+∠B+∠BCA=180°.
为了证明三个角的和
为180°,转化为一个
平角这种转化思想
是数学中的常用方法。
C
B
A
E
1
推理论证
三角形三个内角的和等于180°
已知:△ABC.
求证:∠A+∠B+∠C=180°.
证明:过点A作AE∥BC.
∵∠C+∠EAC=180°,
(两直线平行,同旁内角互补)
即∠C+∠1+∠BAC=180°.
∵ AE∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∴∠C+∠B+∠BAC=180°.
为了证明三个角的和为180°,转化为同旁内角互补,这种转化思想是数学中的常用方法。
三角形三个内角的和等于180°.
温馨提示:利用三角形的内角和定理主要是解决角
的度数问题。
三角形内角和的
几何语言表达
C
B
A
∠A+∠B+∠C=180°.
思考
直角三角形的两个锐角的度数有什么关系呢?
归纳总结
直角三角形的两个锐角互余。
温馨提示:这个性质是直角三角形所特有的哟!
三角形内角和推论
的几何表达
∵∠C=90°,
∴∠A+∠B=90°.
B
A
C
解:∵ ∠A+∠B+∠C=180。,
∠A=80。,∠B=40。,
∴ 80。+40。+∠C=180。,
∴ ∠C=60。.
例题精析
例1 (1)在△ABC中,∠A=80。,∠B=40。,求∠C.
解:
∵ ∠B:∠C =2:3,
例1(2)在△ABC中,∠A=80。,∠B:∠C =2:3,
求∠B,∠C.
例题精析
∴设 ∠B=2x。,∠C =3x。.
∵ ∠A+∠B+∠C=180。, ∠A=80。,
∴ 80。+2x。+3x。=180。,
∴ x=20.
∴∠B=40。,∠C =60。.
解:∵ ∠A+∠B+∠C=180。,
∠A=80。,∠B=3∠C,
∴ 80。+ 3∠C +∠C=180。,
∴ ∠C=25。,
例1(3)在△ABC中,∠A=80。,∠B=3∠C ,
求∠B,∠C.
例题精析
∴ ∠B=75。.
随堂练习
1.在△ABC中,∠A=50。,∠B=∠C ,则∠B= ,
∠C= .
2.在△ABC中,∠A=60。,∠B:∠C =1:2,
则∠B= ,∠C = .
3.在△ABC中,∠A=∠B=4∠C ,则∠A= ,
∠B= ,∠C = .
4.如果三角形的三个内角的度数之比是2:3:4,
则它是( ).
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 钝角或直角三角形
65。
65。
40。
80。
80。
80。
20。
A
1:2:3
C
A
B
D
C
例2 如图,已知在△ABC中,∠C=∠ABC=2∠A,
BD是AC边上的高,求∠DBC的度数。
例题精析
解:∵ ∠A+∠ABC+∠C=180。,
∠C=∠ABC=2∠A,
∴ ∠A+2∠A+2∠A=180。,
∴ ∠A=36。.
∴ ∠C=72。.
∵ BD是AC边上的高,
∴ ∠DBC+∠C=90。,
∴ ∠DBC=18。.
BD平分∠ABC,
∴ ∠ABC=72。.
∵ BD平分∠ABC,
(1)若∠ABC=50。,∠ACB=80。,则∠BOC=______;
(2)若∠A=60。,则∠BOC=_____;
若∠A=80。,则∠BOC= ;
(3)根据(1)、(2)的计算结果猜想∠BOC与∠A之间存在怎样的数量关系?
A
B
C
D
E
O
随堂练习
1.如图,在△ABC中,∠B,∠C的平分线BD、CE
相交于点O.
2.如图,在△ABC中, ∠B<∠C, AD、AE分别
是△ABC的高和角平分线.
(1)若∠B=30。,∠C=50。,则∠DAE=______;
(请直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系,并证明
你的结论。
A
B
C
D
E
1.下列各组图形中,哪一组图形中AD是△ABC的高( ).
A
B
C
D
B
A
B
C
D
C
A
B
C
D
D
A
D
C
B
A
D
B
随堂练习
2.如果一个三角形的三条高的交点恰是三角形的
一个顶点,那么这个三角形是( ).
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 锐角三角形
3.用三角板作△ABC的边BC上的高,下列三角板
的摆放位置正确的是( ).
A B C D
A
4.如图所示,AC⊥BC,CD⊥AB,DE⊥BC,
下列说法中不正确的是( )
A.AC是△ABC的高
B.DE是△BCD的高
C.DE是△ABE的高
D.AD是△ACD的高
C
A
B
C
D
●
●
在三角形中,连接一个顶点与它对边中点的线段叫做三角形这边的中线.
∵ AD是△ABC的中线,
∴BD=CD=
1
2
BC
任意画一个三角形,然后利用刻度尺画出
这个三角形三条边的中线,你发现了什么?
E
F
O
三角形的三条中线相交于一点,交点在三角形的
内部,这个交点叫三角形的重心。
三角形中线的性质
探究发现
随堂练习
1.如图,在△ABC中有四条线段DE,BE,EG,FG,
其中有一条线段是△ABC的中线,则该线段是( ).
A.线段DE B.线段BE
C.线段EG D.线段FG
B
2.如图,D、E分别是△ABC的边AC、BC的中点,
那么下列说法中不正确的是( ).
A.DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BE=EC D.AD=EC,DC=BE
(第1题图)
(第2题图)
D
3.如图,在△ABC中,AD是△ABC的中线,AE是
△ABD的中线,若ED=2 cm,则BC= cm.
8
4.如图,AD,BE,CF是△ABC的三条中线,
则AB=2 =2 ,BD= , AE= .
F
E
D
C
B
A
AF
BF
CD
AC
A
B
C
D
●
●
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
E
F
O
1
2
∵AD是 △ ABC的角平分线,
∴∠ BAD = ∠ CAD =
1
2
∠BAC,
任意画一个三角形,然后利用量角器画出
这个三角形三个角的平分线,你发现什么?
三角形的三条角平分线相交于一点,交点在三角形的内部,这个交点叫做三角形的内心。
∴∠BAC=2∠BAD=2∠CAD.
三角形角平分线的性质
探究发现
三角形的角平分线与角的平分线有什么区别?
思考
三角形的角平分线是一条线段 ,
角的平分线是一条射线.
随堂练习
1.如图,AD、BE、CF为△ABC的三条角平分线,
则∠1= = ,
∠2= = ∠ABC,∠3= = ∠ACB.
∠CAD
∠BAC
∠ABE
∠BCF
2.如图,∠1=∠2,∠3=∠4,下列结论中错误
的是( ).
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.2∠3=∠ACB
D.CE是△ABC的角平分线
D
3.如图,已知CD、CE、CF分别是△ABC的高、
角平分线、中线,则下列各式中错误的是( ).
A.AB=2BF
B.∠ACE= ∠ACB
C.AE=BE
D.CD⊥BE
C
课堂小结
一.三角形的高:
从三角形的一个顶点向它对边所在的直线作垂线,顶点和垂足之间的线段.
锐角三角形的三条高都在三角形的内部,交于同一点.
直角三角形的三条高交于直角顶点.
钝角三角形的三条高不相交于一点,高所在直线交于一点.
三角形的三条高所在直线交于一点.(垂心)
二.三角形的中线:
在三角形中,连接一个顶点与它对边中点的线段.
三角形的三条中线相交于一点,交点在三角形的
内部,这个交点叫三角形的重心。
三.三角形的角平分线:
在三角形中,一个内角的角平分线与它的对边相交,
这个角的顶点与交点之间的线段,叫做三角形的
角平分线.
三角形的三条角平分线相交于一点,交点在三角形
的内部,这个交点叫做三角形的内心。
注意:三角形的角平分线是一条线段 ,
角的平分线是一条射线.
作业与课外学习任务
1.练习作业:学习检测P54-55 第1至10题
书面课本P76 练习 1,2
2.课外学习任务:
预习P76 9.1.2 三角形的内角和与外角和
教学反馈:
作业存在的主要问题:
2.如图,在△ABC中, ∠B<∠C, AD、AE分别
是△ABC的高和角平分线.
(1)若∠B=30。,∠C=50。,则∠DAE=______;
(请直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系,并证明
你的结论。
A
B
C
D
E
2.如图,在△ABC中, ∠B<∠C, AD、AE分别
是△ABC的高和角平分线.
(2)写出∠DAE、∠B、∠C的数量关系,并证明
你的结论。
A
B
C
D
E
∵ AD是△ABC的高,
∴ ∠ADC=90。.
∴ ∠DAC=180。-∠ADC-∠C,
=90。-∠C.
∵ AE是△ABC的角平分线,
∵ ∠BAC=180。-∠B-∠C,
∴ ∠DAE=∠EAC-∠DAC,
2.如图,在△ABC中, ∠B<∠C, AD、AE分别
是△ABC的高和角平分线.
(2)写出∠DAE、∠B、∠C的数量关系,并证明
你的结论。
A
B
C
D
E
∵ AD是△ABC的高,
∴ ∠ADC=90。.
∴ ∠DAC=180。-∠ADC-∠C,
=90。-∠C.
∵ AE是△ABC的角平分线,
∵ ∠BAC=180。-∠B-∠C,
∴ ∠DAE=∠EAC-∠DAC,
课堂小结
一.三角形的内角和:
三角形三个内角的和等于180°.
课堂小结
三角形的内角和:
三角形三个内角的和等于180°.
C
B
A
在△ABC中, ∠A+∠B+∠C=180°.
直角三角形的两个锐角互余。
B
A
C
在△ABC中, 若∠C=90°,
则∠A+∠B=90°.
作业与课外学习任务
1.练习作业:学习检测P56-57 第1至12题
书面课本P82 习题9.1 1,2
2.课外学习任务:
预习P76 9.1.2 三角形的外角和
9.1 三 角 形
2.三角形的内角和与外角和
教学目标
教学重点与难点
重点:三角形的内角和与外角和,三角形的外角的两条性质及应用.
难点:三角形的外角的两条性质及其应用.
1. 理解和掌握三角形的内角和等于180o并会应用.
2.理解和掌握三角形的外角和等于360o并会应用.
3.理解和掌握三角形的外角的两条性质及其应用.
O
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
温故夯基
一.三角形的高:
从三角形的一个顶点向它对边所在的直线作垂线,顶点和垂足之间的线段.
A
B
C
●
直角三角形的三条高交于直角顶点.
A
B
C
D
E
F
钝角三角形的三条高不相交于一点.
钝角三角形的三条高
所在直线交于一点
三角形的三条高所在直线交于一点
A
B
C
D
●
●
在三角形中,连接一个顶点与它对边中点的线段叫做三角形这边的中线.
∵ AD是△ABC的中线,
∴BD=CD=
1
2
BC
E
F
O
三角形中线的性质
二.三角形的中线:
三角形的三条中线相交于一点,交点在三角形的
内部,这个交点叫三角形的重心。
A
B
C
D
●
●
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
E
F
O
1
2
∵AD是 △ ABC的角平分线,
∴∠ BAD = ∠ CAD =
1
2
∠BAC,
∴∠BAC=2∠BAD=2∠CAD.
三角形角平分线的性质
三.三角形的角平分线:
三角形的三条角平分线相交于一点,交点在三角形
的内部,这个交点叫做三角形的内心。
巩固练习
1.如果一个三角形的三条高的交点恰是这个三角形
的一个顶点,那么这个三角形是( ).
A.锐角三角形 B.钝角三角形
C.直角三角形 D.等边三角形
C
2.下列线段一定在三角形内部的是( ).
①三角形的三条中线;②三角形的三条高;
③三角形的三条角平分线.
A.①② B.①③ C.②③ D.①②③
B
3.下列说法:
①三角形的角平分线、中线、高都是线段;
②直角三角形只有一条高;
③若一个三角形的三条高都在三角形的内部,
则这个三角形一定是锐角三角形;
④若一个三角形有两条高在三角形的外部,
则这个三角形一定是钝角三角形.
其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
√
×
√
√
C
4.如图,AE⊥BC,BF⊥AC,CD⊥AB,
垂足分别为E,F,D,则△ABC中,
AC边上的高是线段( ).
A.AE B.CD
C.AF D.BF
D
5.如图,AD是△ABC的中线.
(1)若AB=4,AD=3,BC=6,
则△ABD的周长为________;
(2)若AB=4,且△ABD和△ACD的周长之差为1,
则AC=________.
10
3或5
在纸片上画任意的三角形△ABC(把表示三角形三个顶点的字母标在三角形的内部)动手操作剪下内角拼一拼,你能得到什么结论?
A
B
C
问题引入
思考:锐角三角形、直角三角形、钝角三角形的内角和有什么共同特点?
共同特点:三角形的内角和等于180。.
在纸片上画任意的三角形△ABC(把表示三角形三个顶点的字母标在三角形的内部)动手操作剪下内角拼一拼,你能得到什么结论?
A
B
C
B
C
C
A
B
A
B
三角形三个内角的和等于180°.
同学们观察和总结的非常棒,但这只是实验,而观察与实验得到的结论不一定正确,可靠,这样就需要通过数学证明来验证结论是否正确.
从刚才拼角的过程你能想出证明的办法吗?
探究发现
这是一个文字命题,如何转化为几何命题,
结合图形,你能写出已知和求证吗?
C
B
A
求证:∠A+∠B+∠C=180°.
已知:△ABC.
A
C
B
C
B
F
1
E
证明:过点A作EF∥BC ,
∴∠B=∠1,∠C=∠2.
(两直线平行,内错角相等)
∵∠1+∠3+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。
在平面几何里,辅助线通常画成虚线。
三角形三个内角的和等于180°
2
推理论证
三角形三个内角的和等于180°
C
B
A
D
E
1
2
推理论证
已知:△ABC.
求证:∠A+∠B+∠C=180°.
证明:延长BC至点E,过点C作CD∥BA .
∴∠B=∠1,
∠A=∠2.
(两直线平行,同位角相等)
(两直线平行,内错角相等)
∵∠1+∠2+∠BCA=180°,
∴∠A+∠B+∠BCA=180°.
为了证明三个角的和
为180°,转化为一个
平角这种转化思想
是数学中的常用方法。
C
B
A
E
1
推理论证
三角形三个内角的和等于180°
已知:△ABC.
求证:∠A+∠B+∠C=180°.
证明:过点A作AE∥BC.
∵∠C+∠EAC=180°,
(两直线平行,同旁内角互补)
即∠C+∠1+∠BAC=180°.
∵ AE∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∴∠C+∠B+∠BAC=180°.
为了证明三个角的和为180°,转化为同旁内角互补,这种转化思想是数学中的常用方法。
三角形三个内角的和等于180°.
温馨提示:利用三角形的内角和定理主要是解决角
的度数问题。
三角形内角和的
几何语言表达
C
B
A
∠A+∠B+∠C=180°.
思考
直角三角形的两个锐角的度数有什么关系呢?
归纳总结
直角三角形的两个锐角互余。
温馨提示:这个性质是直角三角形所特有的哟!
三角形内角和推论
的几何表达
∵∠C=90°,
∴∠A+∠B=90°.
B
A
C
解:∵ ∠A+∠B+∠C=180。,
∠A=80。,∠B=40。,
∴ 80。+40。+∠C=180。,
∴ ∠C=60。.
例题精析
例1 (1)在△ABC中,∠A=80。,∠B=40。,求∠C.
解:
∵ ∠B:∠C =2:3,
例1(2)在△ABC中,∠A=80。,∠B:∠C =2:3,
求∠B,∠C.
例题精析
∴设 ∠B=2x。,∠C =3x。.
∵ ∠A+∠B+∠C=180。, ∠A=80。,
∴ 80。+2x。+3x。=180。,
∴ x=20.
∴∠B=40。,∠C =60。.
解:∵ ∠A+∠B+∠C=180。,
∠A=80。,∠B=3∠C,
∴ 80。+ 3∠C +∠C=180。,
∴ ∠C=25。,
例1(3)在△ABC中,∠A=80。,∠B=3∠C ,
求∠B,∠C.
例题精析
∴ ∠B=75。.
随堂练习
1.在△ABC中,∠A=50。,∠B=∠C ,则∠B= ,
∠C= .
2.在△ABC中,∠A=60。,∠B:∠C =1:2,
则∠B= ,∠C = .
3.在△ABC中,∠A=∠B=4∠C ,则∠A= ,
∠B= ,∠C = .
4.如果三角形的三个内角的度数之比是2:3:4,
则它是( ).
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 钝角或直角三角形
65。
65。
40。
80。
80。
80。
20。
A
1:2:3
C
A
B
D
C
例2 如图,已知在△ABC中,∠C=∠ABC=2∠A,
BD是AC边上的高,求∠DBC的度数。
例题精析
解:∵ ∠A+∠ABC+∠C=180。,
∠C=∠ABC=2∠A,
∴ ∠A+2∠A+2∠A=180。,
∴ ∠A=36。.
∴ ∠C=72。.
∵ BD是AC边上的高,
∴ ∠DBC+∠C=90。,
∴ ∠DBC=18。.
BD平分∠ABC,
∴ ∠ABC=72。.
∵ BD平分∠ABC,
(1)若∠ABC=50。,∠ACB=80。,则∠BOC=______;
(2)若∠A=60。,则∠BOC=_____;
若∠A=80。,则∠BOC= ;
(3)根据(1)、(2)的计算结果猜想∠BOC与∠A之间存在怎样的数量关系?
A
B
C
D
E
O
随堂练习
1.如图,在△ABC中,∠B,∠C的平分线BD、CE
相交于点O.
2.如图,在△ABC中, ∠B<∠C, AD、AE分别
是△ABC的高和角平分线.
(1)若∠B=30。,∠C=50。,则∠DAE=______;
(请直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系,并证明
你的结论。
A
B
C
D
E
1.下列各组图形中,哪一组图形中AD是△ABC的高( ).
A
B
C
D
B
A
B
C
D
C
A
B
C
D
D
A
D
C
B
A
D
B
随堂练习
2.如果一个三角形的三条高的交点恰是三角形的
一个顶点,那么这个三角形是( ).
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 锐角三角形
3.用三角板作△ABC的边BC上的高,下列三角板
的摆放位置正确的是( ).
A B C D
A
4.如图所示,AC⊥BC,CD⊥AB,DE⊥BC,
下列说法中不正确的是( )
A.AC是△ABC的高
B.DE是△BCD的高
C.DE是△ABE的高
D.AD是△ACD的高
C
A
B
C
D
●
●
在三角形中,连接一个顶点与它对边中点的线段叫做三角形这边的中线.
∵ AD是△ABC的中线,
∴BD=CD=
1
2
BC
任意画一个三角形,然后利用刻度尺画出
这个三角形三条边的中线,你发现了什么?
E
F
O
三角形的三条中线相交于一点,交点在三角形的
内部,这个交点叫三角形的重心。
三角形中线的性质
探究发现
随堂练习
1.如图,在△ABC中有四条线段DE,BE,EG,FG,
其中有一条线段是△ABC的中线,则该线段是( ).
A.线段DE B.线段BE
C.线段EG D.线段FG
B
2.如图,D、E分别是△ABC的边AC、BC的中点,
那么下列说法中不正确的是( ).
A.DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BE=EC D.AD=EC,DC=BE
(第1题图)
(第2题图)
D
3.如图,在△ABC中,AD是△ABC的中线,AE是
△ABD的中线,若ED=2 cm,则BC= cm.
8
4.如图,AD,BE,CF是△ABC的三条中线,
则AB=2 =2 ,BD= , AE= .
F
E
D
C
B
A
AF
BF
CD
AC
A
B
C
D
●
●
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
E
F
O
1
2
∵AD是 △ ABC的角平分线,
∴∠ BAD = ∠ CAD =
1
2
∠BAC,
任意画一个三角形,然后利用量角器画出
这个三角形三个角的平分线,你发现什么?
三角形的三条角平分线相交于一点,交点在三角形的内部,这个交点叫做三角形的内心。
∴∠BAC=2∠BAD=2∠CAD.
三角形角平分线的性质
探究发现
三角形的角平分线与角的平分线有什么区别?
思考
三角形的角平分线是一条线段 ,
角的平分线是一条射线.
随堂练习
1.如图,AD、BE、CF为△ABC的三条角平分线,
则∠1= = ,
∠2= = ∠ABC,∠3= = ∠ACB.
∠CAD
∠BAC
∠ABE
∠BCF
2.如图,∠1=∠2,∠3=∠4,下列结论中错误
的是( ).
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.2∠3=∠ACB
D.CE是△ABC的角平分线
D
3.如图,已知CD、CE、CF分别是△ABC的高、
角平分线、中线,则下列各式中错误的是( ).
A.AB=2BF
B.∠ACE= ∠ACB
C.AE=BE
D.CD⊥BE
C
课堂小结
一.三角形的高:
从三角形的一个顶点向它对边所在的直线作垂线,顶点和垂足之间的线段.
锐角三角形的三条高都在三角形的内部,交于同一点.
直角三角形的三条高交于直角顶点.
钝角三角形的三条高不相交于一点,高所在直线交于一点.
三角形的三条高所在直线交于一点.(垂心)
二.三角形的中线:
在三角形中,连接一个顶点与它对边中点的线段.
三角形的三条中线相交于一点,交点在三角形的
内部,这个交点叫三角形的重心。
三.三角形的角平分线:
在三角形中,一个内角的角平分线与它的对边相交,
这个角的顶点与交点之间的线段,叫做三角形的
角平分线.
三角形的三条角平分线相交于一点,交点在三角形
的内部,这个交点叫做三角形的内心。
注意:三角形的角平分线是一条线段 ,
角的平分线是一条射线.
作业与课外学习任务
1.练习作业:学习检测P54-55 第1至10题
书面课本P76 练习 1,2
2.课外学习任务:
预习P76 9.1.2 三角形的内角和与外角和
教学反馈:
作业存在的主要问题:
2.如图,在△ABC中, ∠B<∠C, AD、AE分别
是△ABC的高和角平分线.
(1)若∠B=30。,∠C=50。,则∠DAE=______;
(请直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系,并证明
你的结论。
A
B
C
D
E
2.如图,在△ABC中, ∠B<∠C, AD、AE分别
是△ABC的高和角平分线.
(2)写出∠DAE、∠B、∠C的数量关系,并证明
你的结论。
A
B
C
D
E
∵ AD是△ABC的高,
∴ ∠ADC=90。.
∴ ∠DAC=180。-∠ADC-∠C,
=90。-∠C.
∵ AE是△ABC的角平分线,
∵ ∠BAC=180。-∠B-∠C,
∴ ∠DAE=∠EAC-∠DAC,
2.如图,在△ABC中, ∠B<∠C, AD、AE分别
是△ABC的高和角平分线.
(2)写出∠DAE、∠B、∠C的数量关系,并证明
你的结论。
A
B
C
D
E
∵ AD是△ABC的高,
∴ ∠ADC=90。.
∴ ∠DAC=180。-∠ADC-∠C,
=90。-∠C.
∵ AE是△ABC的角平分线,
∵ ∠BAC=180。-∠B-∠C,
∴ ∠DAE=∠EAC-∠DAC,
课堂小结
一.三角形的内角和:
三角形三个内角的和等于180°.
课堂小结
三角形的内角和:
三角形三个内角的和等于180°.
C
B
A
在△ABC中, ∠A+∠B+∠C=180°.
直角三角形的两个锐角互余。
B
A
C
在△ABC中, 若∠C=90°,
则∠A+∠B=90°.
作业与课外学习任务
1.练习作业:学习检测P56-57 第1至12题
书面课本P82 习题9.1 1,2
2.课外学习任务:
预习P76 9.1.2 三角形的外角和
