华师大版 八年级下册课件:19.2.1 菱形的性质(共25张PPT)
文档属性
| 名称 | 华师大版 八年级下册课件:19.2.1 菱形的性质(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 00:00:00 | ||
图片预览




文档简介
菱形的性质
数学华师大版 八年级下
新知导入
请观察下列这些图形有什么共同特征?
都有一种特殊的平行四边形——菱形
新知讲解
在平行四边形中,如果内角大小保持不变,仅改变边的长度,请仔细观察和思考:在这变化过程中,哪些关系没变?哪些关系变了?
平行四边形
邻边相等
菱形
如果改变了边的长度,使两邻边相等,那么这个平行四边形成为怎样的四边形?
新知讲解
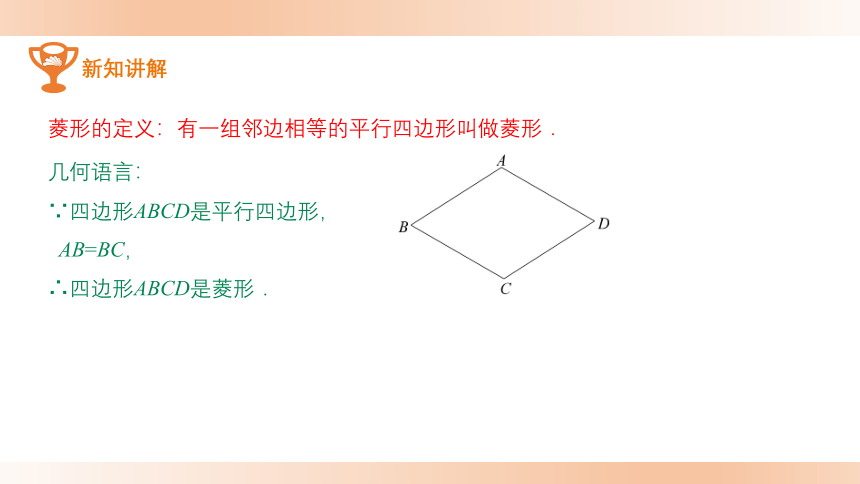
菱形的定义:有一组邻边相等的平行四边形叫做菱形.
几何语言:
∵四边形ABCD是平行四边形,
AB=BC,
∴四边形ABCD是菱形.
新知讲解
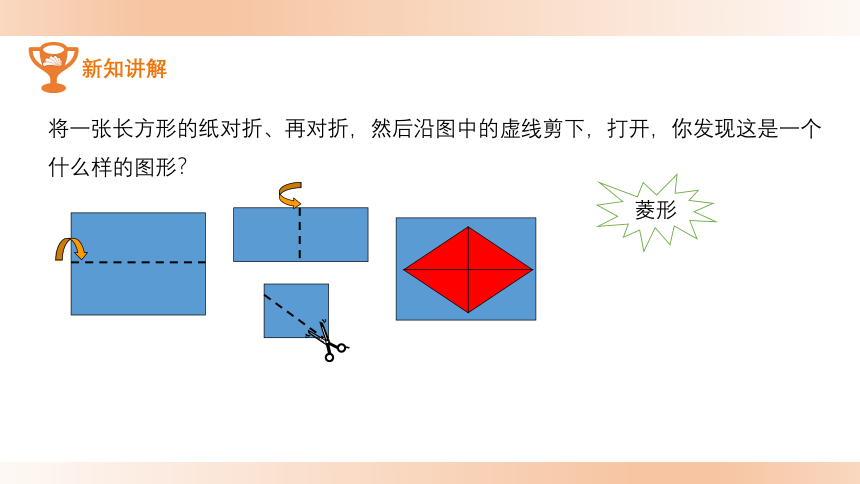
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开,你发现这是一个什么样的图形?
菱形
新知讲解
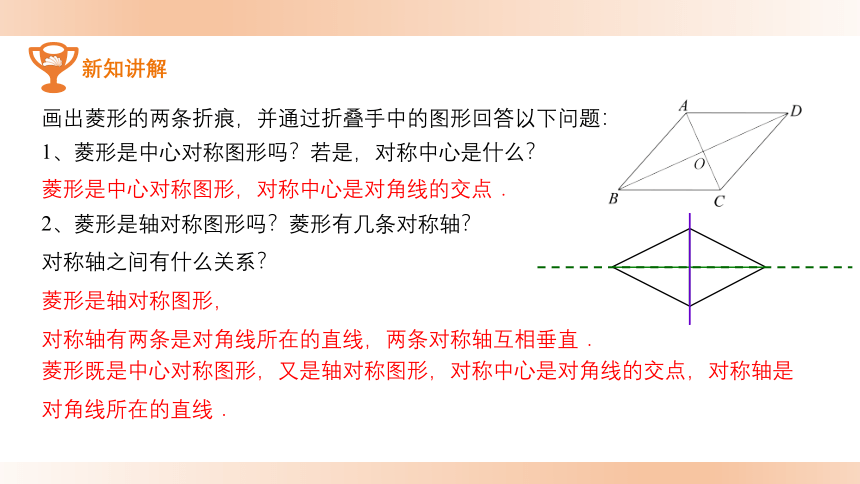
画出菱形的两条折痕,并通过折叠手中的图形回答以下问题:
2、菱形是轴对称图形吗?菱形有几条对称轴?
对称轴之间有什么关系?
1、菱形是中心对称图形吗?若是,对称中心是什么?
菱形是中心对称图形,对称中心是对角线的交点.
菱形是轴对称图形,
对称轴有两条是对角线所在的直线,两条对称轴互相垂直.
菱形既是中心对称图形,又是轴对称图形,对称中心是对角线的交点,对称轴是对角线所在的直线.
新知讲解
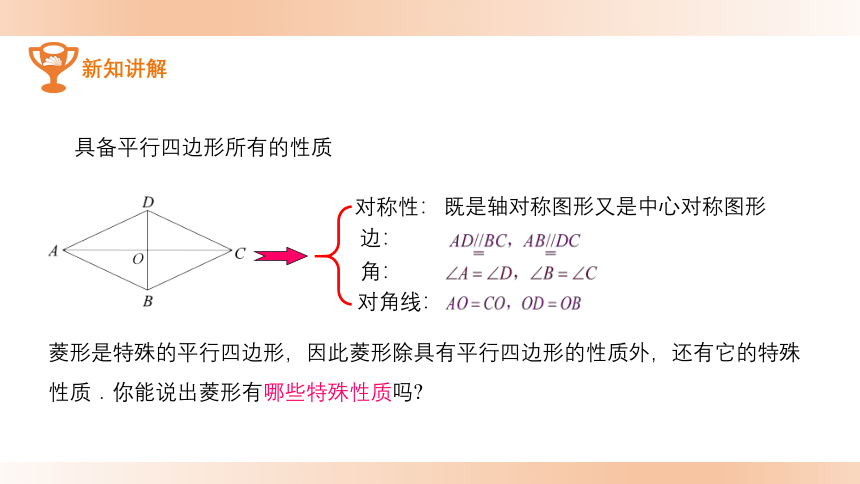
具备平行四边形所有的性质
对称性:
边:
角:
对角线:
既是轴对称图形又是中心对称图形
菱形是特殊的平行四边形,因此菱形除具有平行四边形的性质外,还有它的特殊性质.你能说出菱形有哪些特殊性质吗?
新知讲解
画出菱形的两条对称轴,从边、角、对角线三个方面猜想菱形具有哪些特殊的性质?如何证明?
猜想:
1、菱形的四条边都相等.
2、菱形的对角线互相垂直,且每条对角线对平分一组对角.
如何验证以上的猜想?
新知讲解
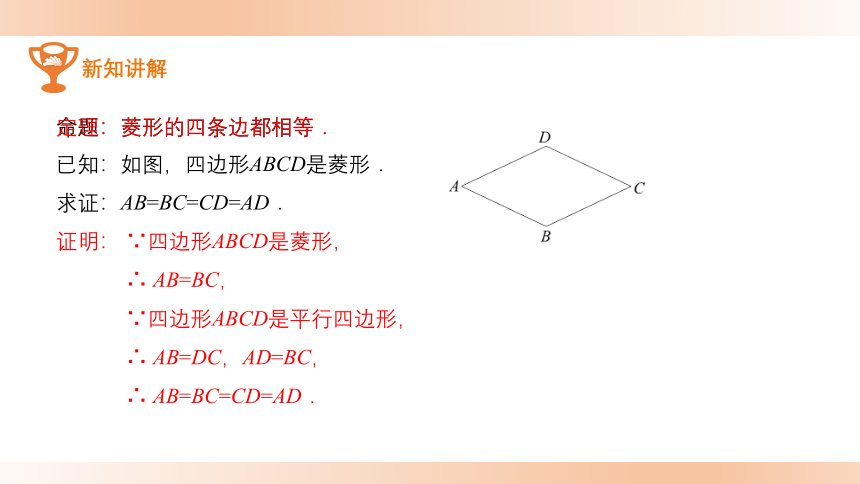
命题:菱形的四条边都相等.
已知:如图,四边形ABCD是菱形.
求证:AB=BC=CD=AD.
证明: ∵四边形ABCD是菱形,
∴ AB=BC,
∵四边形ABCD是平行四边形,
∴ AB=DC,AD=BC,
∴ AB=BC=CD=AD.
定理:菱形的四条边都相等.
新知讲解
命题:菱形的对角线互相垂直,且每条对角线对平分一组对角.
已知:如图,四边形ABCD是菱形.
求证:AC⊥BD ;
AC平分∠DAB和∠DCB;BD平分∠ADC和∠ABC.
证明:∵四边形ABCD是菱形,
∴DA=AB,OB=OD,
在等腰△DAC中,∵AO=CO,
∴DB⊥AC,DB平分∠ADC(三线合一).
同理AC平分∠BCD;BD平分∠ABD和∠ADC.
定理:菱形的对角线互相垂直,且每条对角线对平分一组对角.
新知讲解
{5940675A-B579-460E-94D1-54222C63F5DA}
对称性
边
角
对角线
平行四边形的
一般性性质
矩形的
特殊性质
菱形的
特殊性质
对边平行且相等
邻边垂直
四个角都是直角
中心对称图形
既是中心对称图形又是轴对称图形
对角相等
邻角互补
对角线互相平分
对角线相等
既是中心对称图形又是轴对称图形
四条边相等
对角线互相垂直
平行四边形、矩形、菱形的性质对比
新知讲解
菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形的面积吗?
思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积公式吗?
E
【菱形的面积公式】 S菱形 = 底×高 = 对角线乘积的一半.
新知讲解
例1 如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的大小,并说明△ABC是等边三角形.
解:在菱形ABCD中,∵∠BAD+∠B=180°,∠BAD=2∠B,
∴∠B=60°.
在菱形ABCD中,
∵AB=BC(菱形的四条边都相等),∠B=60°,
∴△ABC是等边三角形.
新知讲解
例2 如图,已知菱形ABCD的边长为2 cm,∠BAD=120°,对角线AC、BD相交于点O.试求这个菱形的两条对角线AC与BD的长.(结果保留根号)
解:∵四边形是ABCD菱形,
∴OB=OD,AB=AD(菱形的四条边都相等),
在△ABO和△ADO中,∵OB=OD,AO=AO,OB=OD,∴△ABO≌△ADO.
∴∠BAO=∠DAO= ∠BAD=60° .
在△ABC中,∵AB=BC,∠BAC=60° ,
∴△ABC为等边三角形,∴AC=AB=2.
在菱形ABCD中,∵AC⊥BD(菱形的对角线互相垂直),
∴△AOB为直角三角形,
∴BO= ,∴BD=2BO= (cm).
新知讲解
例3 如图,菱形ABCD的对角线AC与BD相交于点O,AE垂直且平分CD,垂足为点E.求∠BCD的大小.
解:∵四边形ABCD是菱形,
∴AD=DC=CB=BA(菱形的四条边都相等).
又∵AE垂直平分CD,
∴AC=AD,
∴AC=AD=DC=CB=BA,
即△ADC与△ABC都为等边三角形.
∴∠ACD=∠ACB=60°,
∠BCD=120°.
课堂练习
1、菱形具有而矩形不一定具有的性质是( )
A.对角相等 B.对角线互相垂直
C.对角线互相平分 D.对角线相等
2、下列说法错误的是 ( )
A.菱形的四边都相等
B.菱形的对角线互相垂直
C.菱形的对角线互相平分且平分一组对角
D.菱形的对角线相等且互相平分
B
D
课堂练习
3、如图在菱形ABCD中,对角线AC,BD交与点O,下列说法错误的是( )
A. AB∥CD
B. AC=BD
C.AC ⊥BD
D.OA=OC
4、如图在菱形ABCD中,对角线AC=6,BD=8,AE ⊥BC于点E,则AE的长是( )
A.3 B.2
C.9.6 D.4.8
B
D
课堂练习
5、如图,菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,求菱形的高AE.
解:在菱形ABCD中,
∵AC=6m,BD=8cm,
∴OC= AC= ×6=3cm,OB= BD= ×8=4cm,
∵AC⊥BD,
∴BC=5cm,
∴CD=BC=5cm,S菱形ABCD=CD?AE= AC?BD,
即5AE= ×6×8,解得AE=4.8cm.
课堂练习
6、如图,在菱形ABCD中,过B作BE⊥AD于E,过B作BF⊥CD于F.
求证:AE=CF.
证明:∵菱形ABCD,
∴BA=BC,∠A=∠C,
∵BE⊥AD,BF⊥CD,
∴∠BEA=∠BFC=90°,
在△ABE与△CBF中
∠BEA=∠BFC=90° ,∠A=∠C,BA=BC ,
∴△ABE≌△CBF(AAS),
∴AE=CF.
拓展提高
7、如图,已知菱形ABCD的对角线AC,BD相交于点O,过C作CE⊥AC,交AB的延长线于点E.
(1)求证:四边形BECD是平行四边形;
(2)若∠E=50°,求∠DAB的度数.
拓展提高
(1)证明:∵四边形ABCD是菱形,∴AC⊥BD,DC∥BE,
又∵CE⊥AC,
∴BD∥EC,
∴四边形BECD是平行四边形;
(2)解:∵四边形ABCD是菱形,∴AD=AB,
∴∠ADB=∠ABD,
∵四边形BECD是平行四边形,∴DB∥CE,
∴∠CEA=∠DBA=50°,
∴∠ADB=50°,
∴∠DAB=180°-50°-50°=80°.
中考链接
1、【2018?大连】如图,菱形ABCD中,对角线AC,BD相交于点O,若AB=5,AC=6,则BD的长是( )
A.8 B.7 C.4 D.3
2、【2018?淮安】如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是( )
A.20 B.24 C.40 D.48
A
A
课堂总结
2.思想方法:
S菱形=底×高= 两对角线积的一半.
从知识和思想方法上谈谈你的收获?
(2)探究问题的思维方法:观察—猜想—实验—验证.
1.知识上:
特性"特"在“边、对角线、对称性”.
有一组邻边相等的平行四边形叫菱形.
1个定义;
2个公式;
3个特性;
(1)菱形转化成直角三角形或等腰三角形.
板书设计
菱形的定义:
有一组邻边相等的平行四边形叫做菱形.
菱形的性质定理1:菱形的四条边都相等.
菱形的性质定理2:
菱形的对角线互相垂直,
且每条对角线对平分一组对角.
例1
例2
例3
菱形既是中心对称图形,又是轴对称图形,
对称中心是对角线的交点,对称轴是对角线所在的直线.
作业布置
教材113页第1题、第2题、第3题.
数学华师大版 八年级下
新知导入
请观察下列这些图形有什么共同特征?
都有一种特殊的平行四边形——菱形
新知讲解
在平行四边形中,如果内角大小保持不变,仅改变边的长度,请仔细观察和思考:在这变化过程中,哪些关系没变?哪些关系变了?
平行四边形
邻边相等
菱形
如果改变了边的长度,使两邻边相等,那么这个平行四边形成为怎样的四边形?
新知讲解
菱形的定义:有一组邻边相等的平行四边形叫做菱形.
几何语言:
∵四边形ABCD是平行四边形,
AB=BC,
∴四边形ABCD是菱形.
新知讲解
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开,你发现这是一个什么样的图形?
菱形
新知讲解
画出菱形的两条折痕,并通过折叠手中的图形回答以下问题:
2、菱形是轴对称图形吗?菱形有几条对称轴?
对称轴之间有什么关系?
1、菱形是中心对称图形吗?若是,对称中心是什么?
菱形是中心对称图形,对称中心是对角线的交点.
菱形是轴对称图形,
对称轴有两条是对角线所在的直线,两条对称轴互相垂直.
菱形既是中心对称图形,又是轴对称图形,对称中心是对角线的交点,对称轴是对角线所在的直线.
新知讲解
具备平行四边形所有的性质
对称性:
边:
角:
对角线:
既是轴对称图形又是中心对称图形
菱形是特殊的平行四边形,因此菱形除具有平行四边形的性质外,还有它的特殊性质.你能说出菱形有哪些特殊性质吗?
新知讲解
画出菱形的两条对称轴,从边、角、对角线三个方面猜想菱形具有哪些特殊的性质?如何证明?
猜想:
1、菱形的四条边都相等.
2、菱形的对角线互相垂直,且每条对角线对平分一组对角.
如何验证以上的猜想?
新知讲解
命题:菱形的四条边都相等.
已知:如图,四边形ABCD是菱形.
求证:AB=BC=CD=AD.
证明: ∵四边形ABCD是菱形,
∴ AB=BC,
∵四边形ABCD是平行四边形,
∴ AB=DC,AD=BC,
∴ AB=BC=CD=AD.
定理:菱形的四条边都相等.
新知讲解
命题:菱形的对角线互相垂直,且每条对角线对平分一组对角.
已知:如图,四边形ABCD是菱形.
求证:AC⊥BD ;
AC平分∠DAB和∠DCB;BD平分∠ADC和∠ABC.
证明:∵四边形ABCD是菱形,
∴DA=AB,OB=OD,
在等腰△DAC中,∵AO=CO,
∴DB⊥AC,DB平分∠ADC(三线合一).
同理AC平分∠BCD;BD平分∠ABD和∠ADC.
定理:菱形的对角线互相垂直,且每条对角线对平分一组对角.
新知讲解
{5940675A-B579-460E-94D1-54222C63F5DA}
对称性
边
角
对角线
平行四边形的
一般性性质
矩形的
特殊性质
菱形的
特殊性质
对边平行且相等
邻边垂直
四个角都是直角
中心对称图形
既是中心对称图形又是轴对称图形
对角相等
邻角互补
对角线互相平分
对角线相等
既是中心对称图形又是轴对称图形
四条边相等
对角线互相垂直
平行四边形、矩形、菱形的性质对比
新知讲解
菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形的面积吗?
思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积公式吗?
E
【菱形的面积公式】 S菱形 = 底×高 = 对角线乘积的一半.
新知讲解
例1 如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的大小,并说明△ABC是等边三角形.
解:在菱形ABCD中,∵∠BAD+∠B=180°,∠BAD=2∠B,
∴∠B=60°.
在菱形ABCD中,
∵AB=BC(菱形的四条边都相等),∠B=60°,
∴△ABC是等边三角形.
新知讲解
例2 如图,已知菱形ABCD的边长为2 cm,∠BAD=120°,对角线AC、BD相交于点O.试求这个菱形的两条对角线AC与BD的长.(结果保留根号)
解:∵四边形是ABCD菱形,
∴OB=OD,AB=AD(菱形的四条边都相等),
在△ABO和△ADO中,∵OB=OD,AO=AO,OB=OD,∴△ABO≌△ADO.
∴∠BAO=∠DAO= ∠BAD=60° .
在△ABC中,∵AB=BC,∠BAC=60° ,
∴△ABC为等边三角形,∴AC=AB=2.
在菱形ABCD中,∵AC⊥BD(菱形的对角线互相垂直),
∴△AOB为直角三角形,
∴BO= ,∴BD=2BO= (cm).
新知讲解
例3 如图,菱形ABCD的对角线AC与BD相交于点O,AE垂直且平分CD,垂足为点E.求∠BCD的大小.
解:∵四边形ABCD是菱形,
∴AD=DC=CB=BA(菱形的四条边都相等).
又∵AE垂直平分CD,
∴AC=AD,
∴AC=AD=DC=CB=BA,
即△ADC与△ABC都为等边三角形.
∴∠ACD=∠ACB=60°,
∠BCD=120°.
课堂练习
1、菱形具有而矩形不一定具有的性质是( )
A.对角相等 B.对角线互相垂直
C.对角线互相平分 D.对角线相等
2、下列说法错误的是 ( )
A.菱形的四边都相等
B.菱形的对角线互相垂直
C.菱形的对角线互相平分且平分一组对角
D.菱形的对角线相等且互相平分
B
D
课堂练习
3、如图在菱形ABCD中,对角线AC,BD交与点O,下列说法错误的是( )
A. AB∥CD
B. AC=BD
C.AC ⊥BD
D.OA=OC
4、如图在菱形ABCD中,对角线AC=6,BD=8,AE ⊥BC于点E,则AE的长是( )
A.3 B.2
C.9.6 D.4.8
B
D
课堂练习
5、如图,菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,求菱形的高AE.
解:在菱形ABCD中,
∵AC=6m,BD=8cm,
∴OC= AC= ×6=3cm,OB= BD= ×8=4cm,
∵AC⊥BD,
∴BC=5cm,
∴CD=BC=5cm,S菱形ABCD=CD?AE= AC?BD,
即5AE= ×6×8,解得AE=4.8cm.
课堂练习
6、如图,在菱形ABCD中,过B作BE⊥AD于E,过B作BF⊥CD于F.
求证:AE=CF.
证明:∵菱形ABCD,
∴BA=BC,∠A=∠C,
∵BE⊥AD,BF⊥CD,
∴∠BEA=∠BFC=90°,
在△ABE与△CBF中
∠BEA=∠BFC=90° ,∠A=∠C,BA=BC ,
∴△ABE≌△CBF(AAS),
∴AE=CF.
拓展提高
7、如图,已知菱形ABCD的对角线AC,BD相交于点O,过C作CE⊥AC,交AB的延长线于点E.
(1)求证:四边形BECD是平行四边形;
(2)若∠E=50°,求∠DAB的度数.
拓展提高
(1)证明:∵四边形ABCD是菱形,∴AC⊥BD,DC∥BE,
又∵CE⊥AC,
∴BD∥EC,
∴四边形BECD是平行四边形;
(2)解:∵四边形ABCD是菱形,∴AD=AB,
∴∠ADB=∠ABD,
∵四边形BECD是平行四边形,∴DB∥CE,
∴∠CEA=∠DBA=50°,
∴∠ADB=50°,
∴∠DAB=180°-50°-50°=80°.
中考链接
1、【2018?大连】如图,菱形ABCD中,对角线AC,BD相交于点O,若AB=5,AC=6,则BD的长是( )
A.8 B.7 C.4 D.3
2、【2018?淮安】如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是( )
A.20 B.24 C.40 D.48
A
A
课堂总结
2.思想方法:
S菱形=底×高= 两对角线积的一半.
从知识和思想方法上谈谈你的收获?
(2)探究问题的思维方法:观察—猜想—实验—验证.
1.知识上:
特性"特"在“边、对角线、对称性”.
有一组邻边相等的平行四边形叫菱形.
1个定义;
2个公式;
3个特性;
(1)菱形转化成直角三角形或等腰三角形.
板书设计
菱形的定义:
有一组邻边相等的平行四边形叫做菱形.
菱形的性质定理1:菱形的四条边都相等.
菱形的性质定理2:
菱形的对角线互相垂直,
且每条对角线对平分一组对角.
例1
例2
例3
菱形既是中心对称图形,又是轴对称图形,
对称中心是对角线的交点,对称轴是对角线所在的直线.
作业布置
教材113页第1题、第2题、第3题.
