16.1二次根式(2) 课件(共25张PPT)
文档属性
| 名称 | 16.1二次根式(2) 课件(共25张PPT) |  | |
| 格式 | rar | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 09:00:44 | ||
图片预览








文档简介
(共25张PPT)
人教版
八年级数学下
16.1二次根式(2)
教学目标
1.经历二次根式的性质的发现过程,体验归纳、猜想的
思想方法.(重点)
2.会运用二次根式的两个性质进行化简计算.(难点)
回顾旧知
断一断:判断下列各式中那些是二次根式?
?
?
?
?
?
?
?
?
?
?
温馨提示:(1)根指数必须为2;(2)被开方数必须是非负数。
合作探究---二次根式的性质
探究1 根据算术平方根的意义填空,并说出得到结论的依据。
4
2
0
.
同理
分别是0,4,
的算术平方根,即得上面的等式.
是2的算术平方根,根据算术平方根的意义,
是一个平方等于2的非负数.因此
你能将上述规律推广到一般吗?如何用字母来表示。
合作探究---二次根式的性质
归纳:
的性质1:
一般地,
=a
(a
≥0).
即:一个非负数的算术平方根的平方等于它本身.
即:利用这个式子,我们可以把任何一个非负数写成一个数的平方的形式。
根据等式的定义,可得:
a=
(a
≥0).
典例精讲
例1
计算:
解:
(2)可以用到幂的哪条基本性质呢?
积的乘方:
(ab)2=a2b2
合作探究---二次根式的性质
...
平方运算
算术平方根
2
0.1
0
...
a(a≥0)
2
...
观察两者有什么关系?
填一填:
=a
(a≥0).
合作探究---二次根式的性质
...
平方运算
算术平方根
-2
-0.1
...
2
...
观察两者有什么关系?
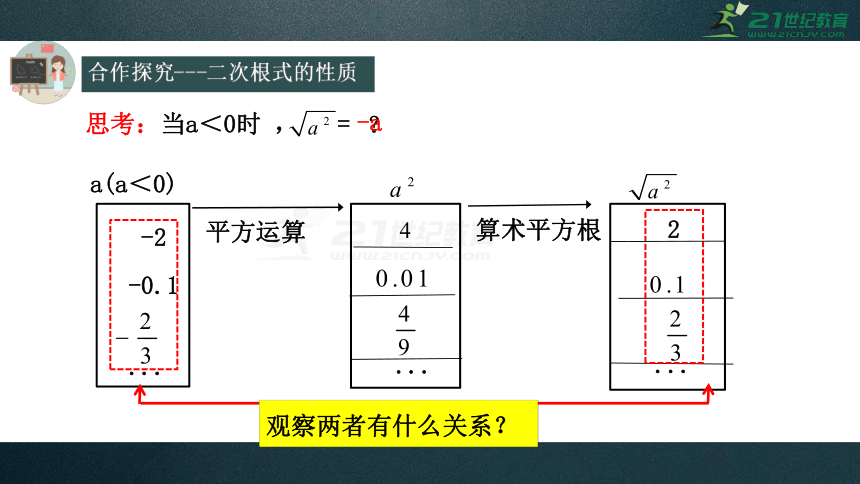
a(a<0)
思考:当a<0时
,
=
?
-a
合作探究---二次根式的性质
a
(a≥0)
-a
(a<0)
即:任意一个数的平方的算术平方根等于它本身的绝对值.
归纳:
的性质2:
即:利用这个式子,可以把任何一个非负数写成带有“
”的形式。
根据等式的定义,可得:
a
=
(a≥0).
典例精讲
例2
化简:
解:
典例精析
例3
在实数范围内分解因式:
解:
小试牛刀
1、断一断:请同学们快速分辨下列各题的对错.
(
)
(
)
(
)
(
)
×
×
√
√
小试牛刀
2、
计算:
解:
小试牛刀
思考:如何区别
与
?
运算顺序
取值范围
运算结果
先开方,后平方
先平方,后开方
a≥0
a取任何实数
a
|a|
意义
表示一个非负数a的算术平方根的平方
表示一个实数a的平方的算术平方根
小试牛刀
3、实数a、b在数轴上的对应点如图所示,请你化简:
解:由数轴可知a<0,b>0,a-b<0,
∴原式=|a|-|b|+|a-b|
=-a-b-(a-b)
=-2a.
a
b
合作探究
用基本运算符号(包括加、减、乘、除、乘方和开方)把
或
.
连接起来的式子,我们称这样的式子为代数式.
数
表示数的字母
思考:到现在为止,初中阶段所学的代数式主要有哪几类?
代数式
整式
分式
二次根式
小试牛刀
1.下列式子是代数式的有
(
)
①a2+b2
;
②
;
③13;
④x=2;
⑤3×(4
-5);
⑥x-1≤0;
⑦10x+5y=15
;
⑧
A.3个
B.4个
C.5个
D.6个
C
温馨提示:单独的一个数是代数式,用等号或不等号连接起来的式子都不是代数式。
小试牛刀
?
小试牛刀
?
小试牛刀
?
课堂小结
本节课你有哪些收获?
1、二次根式的性质1、性质2分别是什么?
2、什么是代数式?
综合演练
1.化简
得(
)
A.
±4
B.
±2
C.
4
D.-4
C
2.
当1的值为(
)
A.3
B.-3
C.1
D.-1
D
3.在下列各式中,不是代数式的是( )
A.7
B.3>2
C.
D.
B
综合演练
4.化简:
(1)
=
;
(2)
=
;
(3)
;
(4)
.
3
7
4
81
5.
实数a在数轴上的位置如图所示,化简
的结果是
.
-1
0
1
2
a
1
综合演练
6、已知a、b、c是△ABC的三边长,化简:
解:∵a、b、c是△ABC的三边长,
∴a+b>c,b+c>a,b+a>c,
∴原式=|a+b+c|-|b+c-a|+|c-b-a|
=a+b+c-(b+c-a)+(b+a-c)
=a+b+c-b-c+a+b+a-c
=3a+b-c.
知识点拨:利用三角形三边关系:三边长均为正数,a+b>c两边之和大于第三边,b+c-a>0,c-b-a<0
课后作业
习题16.1
P5:2、3、4
人教版
八年级数学下
16.1二次根式(2)
教学目标
1.经历二次根式的性质的发现过程,体验归纳、猜想的
思想方法.(重点)
2.会运用二次根式的两个性质进行化简计算.(难点)
回顾旧知
断一断:判断下列各式中那些是二次根式?
?
?
?
?
?
?
?
?
?
?
温馨提示:(1)根指数必须为2;(2)被开方数必须是非负数。
合作探究---二次根式的性质
探究1 根据算术平方根的意义填空,并说出得到结论的依据。
4
2
0
.
同理
分别是0,4,
的算术平方根,即得上面的等式.
是2的算术平方根,根据算术平方根的意义,
是一个平方等于2的非负数.因此
你能将上述规律推广到一般吗?如何用字母来表示。
合作探究---二次根式的性质
归纳:
的性质1:
一般地,
=a
(a
≥0).
即:一个非负数的算术平方根的平方等于它本身.
即:利用这个式子,我们可以把任何一个非负数写成一个数的平方的形式。
根据等式的定义,可得:
a=
(a
≥0).
典例精讲
例1
计算:
解:
(2)可以用到幂的哪条基本性质呢?
积的乘方:
(ab)2=a2b2
合作探究---二次根式的性质
...
平方运算
算术平方根
2
0.1
0
...
a(a≥0)
2
...
观察两者有什么关系?
填一填:
=a
(a≥0).
合作探究---二次根式的性质
...
平方运算
算术平方根
-2
-0.1
...
2
...
观察两者有什么关系?
a(a<0)
思考:当a<0时
,
=
?
-a
合作探究---二次根式的性质
a
(a≥0)
-a
(a<0)
即:任意一个数的平方的算术平方根等于它本身的绝对值.
归纳:
的性质2:
即:利用这个式子,可以把任何一个非负数写成带有“
”的形式。
根据等式的定义,可得:
a
=
(a≥0).
典例精讲
例2
化简:
解:
典例精析
例3
在实数范围内分解因式:
解:
小试牛刀
1、断一断:请同学们快速分辨下列各题的对错.
(
)
(
)
(
)
(
)
×
×
√
√
小试牛刀
2、
计算:
解:
小试牛刀
思考:如何区别
与
?
运算顺序
取值范围
运算结果
先开方,后平方
先平方,后开方
a≥0
a取任何实数
a
|a|
意义
表示一个非负数a的算术平方根的平方
表示一个实数a的平方的算术平方根
小试牛刀
3、实数a、b在数轴上的对应点如图所示,请你化简:
解:由数轴可知a<0,b>0,a-b<0,
∴原式=|a|-|b|+|a-b|
=-a-b-(a-b)
=-2a.
a
b
合作探究
用基本运算符号(包括加、减、乘、除、乘方和开方)把
或
.
连接起来的式子,我们称这样的式子为代数式.
数
表示数的字母
思考:到现在为止,初中阶段所学的代数式主要有哪几类?
代数式
整式
分式
二次根式
小试牛刀
1.下列式子是代数式的有
(
)
①a2+b2
;
②
;
③13;
④x=2;
⑤3×(4
-5);
⑥x-1≤0;
⑦10x+5y=15
;
⑧
A.3个
B.4个
C.5个
D.6个
C
温馨提示:单独的一个数是代数式,用等号或不等号连接起来的式子都不是代数式。
小试牛刀
?
小试牛刀
?
小试牛刀
?
课堂小结
本节课你有哪些收获?
1、二次根式的性质1、性质2分别是什么?
2、什么是代数式?
综合演练
1.化简
得(
)
A.
±4
B.
±2
C.
4
D.-4
C
2.
当1
)
A.3
B.-3
C.1
D.-1
D
3.在下列各式中,不是代数式的是( )
A.7
B.3>2
C.
D.
B
综合演练
4.化简:
(1)
=
;
(2)
=
;
(3)
;
(4)
.
3
7
4
81
5.
实数a在数轴上的位置如图所示,化简
的结果是
.
-1
0
1
2
a
1
综合演练
6、已知a、b、c是△ABC的三边长,化简:
解:∵a、b、c是△ABC的三边长,
∴a+b>c,b+c>a,b+a>c,
∴原式=|a+b+c|-|b+c-a|+|c-b-a|
=a+b+c-(b+c-a)+(b+a-c)
=a+b+c-b-c+a+b+a-c
=3a+b-c.
知识点拨:利用三角形三边关系:三边长均为正数,a+b>c两边之和大于第三边,b+c-a>0,c-b-a<0
课后作业
习题16.1
P5:2、3、4
