五年级数学上册课件-8. 总复习人教版(共54张PPT)
文档属性
| 名称 | 五年级数学上册课件-8. 总复习人教版(共54张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 00:00:00 | ||
图片预览








文档简介
(共54张PPT)
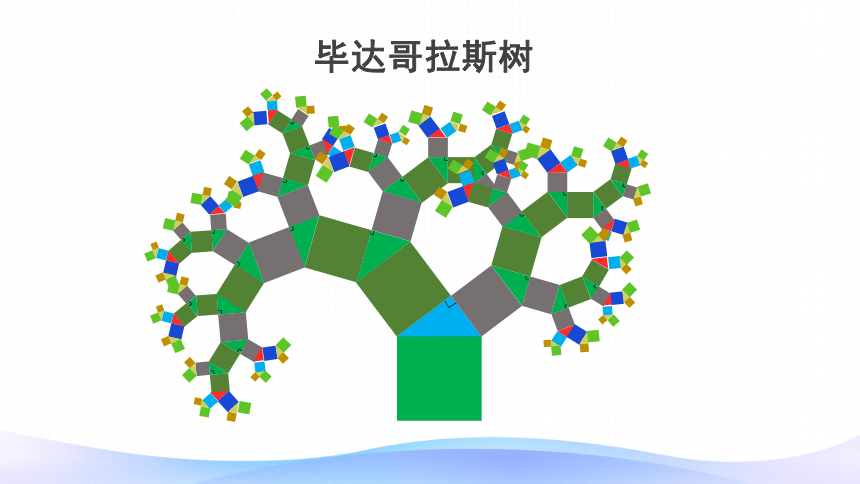
走近毕达哥拉斯树
毕达哥拉斯树
这个树全是由正方形和三角形组成的。
这些三角形全部都是直角三角形。
每个直角三角形的周围都有三个正方形。
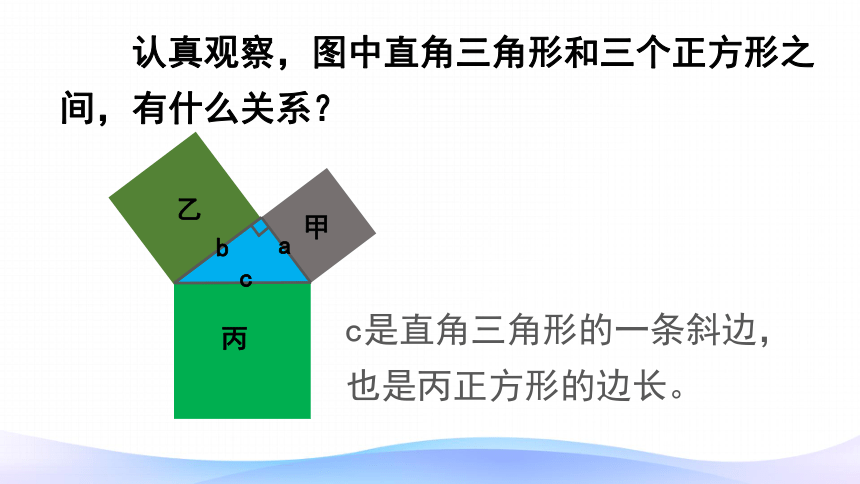
甲
乙
a
b
c
丙
认真观察,图中直角三角形和三个正方形之间,有什么关系?
直角三角形的三条边就是三个正方形的边长。
a是直角三角形的一条直角边。
a是甲正方形的边长。
甲
乙
a
b
c
丙
认真观察,图中直角三角形和三个正方形之间,有什么关系?
b是直角三角形的一条直角边,也是乙正方形的边长。
甲
乙
a
b
c
丙
认真观察,图中直角三角形和三个正方形之间,有什么关系?
c是直角三角形的一条斜边,
也是丙正方形的边长。
甲
乙
a
b
c
丙
甲
乙
a
b
c
丙
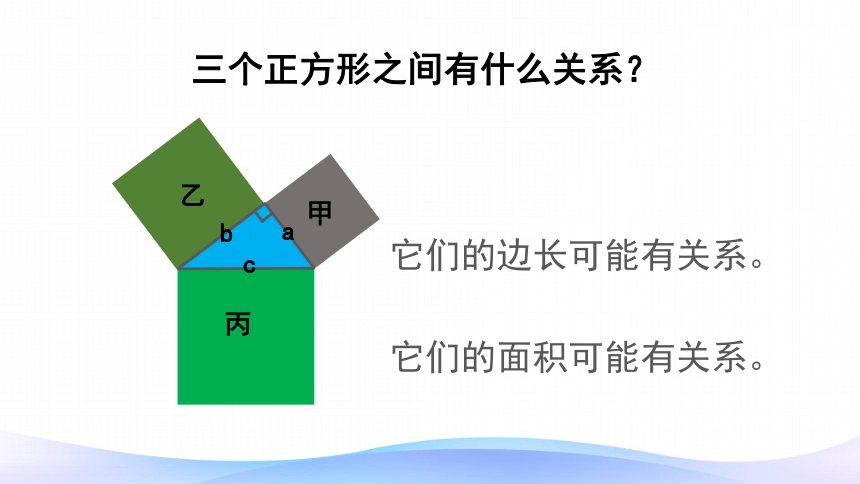
三个正方形之间有什么关系?
它们的面积可能有关系。
它们的边长可能有关系。
三个正方形之间有什么关系?
才能求出正方形的面积。
知道正方形的边长。
甲
乙
a
b
c
丙
算出三个正方形的面积,分别是多少?
甲
乙
3
4
5
丙
乙的面积是(
)cm2
甲的面积是(
)cm2
丙的面积是(
)cm2
9
16
25
S=a2
3×3=9cm2
=16cm2
4×4
单位:cm
甲、乙、丙三个正方形的面积之间,有什么关系?
甲
乙
3
4
5
丙
乙的面积是(
)cm2
甲的面积是(
)cm2
丙的面积是(
)cm2
16
25
甲的面积加上乙的面积等于丙的面积。
单位:cm
9
甲、乙、丙三个正方形的面积之间,有什么关系?
甲
乙
3
4
5
丙
=25cm2
9cm2+16cm2
S甲+S乙
=S丙
单位:cm
乙的面积是(
)cm2
甲的面积是(
)cm2
丙的面积是(
)cm2
16
25
9
甲
乙
a
b
c
丙
甲、乙、丙三个正方形的面积之间,有什么关系?
甲
乙
3
4
5
丙
=25cm2
9cm2+16cm2
S甲+S乙
=S丙
单位:cm
乙的面积是(
)cm2
甲的面积是(
)cm2
丙的面积是(
)cm2
16
25
9
以任意直角三角形的三条边分别为边长,向外做三个正方形,是否都能得到这种关系呢?
甲
乙
3
4
5
丙
S甲+S乙
=S丙
单位:cm
毕达哥拉斯树
单位:cm
甲
乙
丙
5.7
7.6
2.我们的发现:
1.填空:
甲的边长是(
)cm,S甲=(
)cm2
S甲+S乙=(
)+(
)=(
)cm2
乙的边长是(
)cm,S乙=(
)cm2
丙的边长是(
)cm,S丙=(
)cm2
9.5
丙
活动要求
(一)4人小组合作,1人报数据,2人用
计算器计算,确保计算的结果正确,还有1
人做记录。
(二)4人一起说一说你们的发现,再把它
记录下来。
单位:cm
甲
乙
丙
5.7
7.6
2.我们的发现:
1.填空:
甲的边长是(
)cm,S甲=(
)cm2
S甲+S乙=(
)+(
)=(
)cm2
乙的边长是(
)cm,S乙=(
)cm2
丙的边长是(
)cm,S丙=(
)cm2
9.5
丙
单位:cm
甲
乙
丙
5.7
7.6
2.我们的发现:
1.填空:
甲的边长是(
)cm,S甲=(
)cm2
S甲+S乙=(
)+(
)=(
)cm2
乙的边长是(
)cm,S乙=(
)cm2
丙的边长是(
)cm,S丙=(
)cm2
9.5
丙
5.7
32.49
7.6
57.76
9.5
90.25
32.49
57.76
90.25
S甲+S乙=S丙
单位:cm
2.我们的发现:
1.填空:
甲的边长是(
)cm,S甲=(
)cm2
S甲+S乙=(
)+(
)=(
)cm2
乙的边长是(
)cm,S乙=(
)cm2
丙的边长是(
)cm,S丙=(
)cm2
甲
乙
丙
1.3
8.4
8.5
丙
1.3
1.69
8.4
70.56
8.5
72.25
1.69
70.56
72.25
S甲+S乙=S丙
单位:cm
甲
乙
丙
16
30
2.我们的发现:
1.填空:
甲的边长是(
)cm,S甲=(
)cm2
S甲+S乙=(
)+(
)=(
)cm2
乙的边长是(
)cm,S乙=(
)cm2
丙的边长是(
)cm,S丙=(
)cm2
34
丙
16
256
30
900
34
1156
256
900
1156
S甲+S乙=S丙
单位:cm
甲
乙
丙
3.3
5.6
2.我们的发现:
1.填空:
甲的边长是(
)cm,S甲=(
)cm2
S甲+S乙=(
)+(
)=(
)cm2
乙的边长是(
)cm,S乙=(
)cm2
丙的边长是(
)cm,S丙=(
)cm2
6.5
丙
3.3
10.89
5.6
31.36
6.5
42.25
10.89
31.36
42.25
S甲+S乙=S丙
单位:cm
2.我们的发现:
1.填空:
甲的边长是(
)cm,S甲=(
)cm2
S甲+S乙=(
)+(
)=(
)cm2
乙的边长是(
)cm,S乙=(
)cm2
丙的边长是(
)cm,S丙=(
)cm2
甲
乙
丙
1.1
6
6.1
丙
1.1
1.21
6
36
6.1
37.21
1.21
36
37.21
S甲+S乙=S丙
S甲+S乙=S丙
S甲+S乙=S丙
S甲+S乙=S丙
虽然每一组研究的数据不一样,但是结论都一样。
S甲+S乙=S丙
一句话概括刚才所有的发现。
任意一个直角三角形的三
条边,向外分别作三个正方形,
都是甲的面积加上乙的面积等于
丙的面积。
甲
乙
丙
丙
甲
乙
a
b
c
丙
S甲+S乙=S丙
甲
乙
a
b
c
丙
a?+b?=c?
a、b、c之间,有什么关系?
=a?
S甲=a×a
=b?
S乙=b×b
=c?
S丙=c×c
S甲+S乙=S丙
甲
乙
a
b
c
丙
a
b
c
a?+b?=c?
它不仅是三个正方形的边长
之间的关系,还是直角三角形中
三条边之间的关系。
直角边
另一条直角边
斜边
在直角三角形中,两直角边的平方和才会等于斜边的平方。
a
b
c
一条直角边的平方加另一条直角
边的平方等于斜边的平方。
直角边
另一条直角边
斜边
a?+b?=c?,在直角三角形中表示什么意思?
两条直角边的平方和,等于
斜边的平方。
a
b
c
a?+b?=c?
钝角三角形和锐角三角形,是不是也存在这种关系?
提出一个问题,比解决问题更重要。
a
b
c
a?+b?=c?
钝角三角形和锐角三角形,是不是也存在这种关系?
C(12)
a(6)
b(8)
a2+b2=c2,在锐角三角形、钝角三角形中是否适用呢?
a(6)
b(8)
C(9)
单位:cm
适用,因为它们都是三角形,都有三条边。
不适用,因为直角三角形中有直角,而钝角三角形和锐角三角形它们没有,它们不一样。
a2+b2=(
)cm2
a2+b2
c2
>
c2=(
)cm2
a2+b2=c2,在锐角三角形、钝角三角形中是否适用呢?
a2=(
)cm2
b2=(
)cm2
a(6)
b(8)
C(9)
36
64
100
81
在锐角三角形中,a?+b?=c?不适用。
a2+b2=c2,在锐角三角形、钝角三角形中是否适用呢?
C(12)
a(6)
b(8)
a2+b2=(
)cm2
a2+b2
c2
<
c2=(
)cm2
a2=(
)cm2
b2=(
)cm2
36
64
100
144
a?+b?=c?,不适用于钝角三角形。
a?+b?=c?
在锐角三角形和钝角三角形中都不适用。
直角三角形所特有的三边关系。
a是6厘米,b是8厘米,要使a和b的夹角是90度,组成直角三角形,c会是(
)厘米。
C(?
)
a(6)
b(8)
10
a?+b?=6?+8?=100cm2
a?+b?=c?=100cm2
10×10=100
c=10cm
直角三角形的三边关系
毕达哥拉斯树
a
b
c
a?+b?=c?
在直角三角形中,两直角边的平方和
等于斜边的平方。
直角边
另一条直角边
斜边
a?+b?=c?
毕达哥拉斯定理
一天,毕达哥拉斯应邀到朋友家做客。
他无意间发现主人家地面上铺着一块块漂亮
的正方形地砖,地砖的图案深深吸引着他。
他发现这些大小如一的地砖排列是有规律的,
彼此间产生着某种数量关系。
他索性拿出笔在地砖上画起图形,经过无
数次的验证,他得到“在直角三角形中,两直
角边的平方和等于斜边的平方”这一数量关系
是成立的。为了庆祝自己的发现,他屠杀了
100头牛庆祝。后来人们为了纪念他,把他的
发现叫做“毕达格拉斯定理”,也叫“百牛定
理”。
毕达哥拉斯树
毕达哥拉斯树
毕达哥拉斯定理
毕达哥拉斯定理,在中国叫做勾
股定理。早在3000多年前,我国数学
家商高就提出“勾三、股四、弦五”
的说法,我国就称它为“勾股定理”,
又叫“商高定理”。
3
4
5
再见!
走近毕达哥拉斯树
毕达哥拉斯树
这个树全是由正方形和三角形组成的。
这些三角形全部都是直角三角形。
每个直角三角形的周围都有三个正方形。
甲
乙
a
b
c
丙
认真观察,图中直角三角形和三个正方形之间,有什么关系?
直角三角形的三条边就是三个正方形的边长。
a是直角三角形的一条直角边。
a是甲正方形的边长。
甲
乙
a
b
c
丙
认真观察,图中直角三角形和三个正方形之间,有什么关系?
b是直角三角形的一条直角边,也是乙正方形的边长。
甲
乙
a
b
c
丙
认真观察,图中直角三角形和三个正方形之间,有什么关系?
c是直角三角形的一条斜边,
也是丙正方形的边长。
甲
乙
a
b
c
丙
甲
乙
a
b
c
丙
三个正方形之间有什么关系?
它们的面积可能有关系。
它们的边长可能有关系。
三个正方形之间有什么关系?
才能求出正方形的面积。
知道正方形的边长。
甲
乙
a
b
c
丙
算出三个正方形的面积,分别是多少?
甲
乙
3
4
5
丙
乙的面积是(
)cm2
甲的面积是(
)cm2
丙的面积是(
)cm2
9
16
25
S=a2
3×3=9cm2
=16cm2
4×4
单位:cm
甲、乙、丙三个正方形的面积之间,有什么关系?
甲
乙
3
4
5
丙
乙的面积是(
)cm2
甲的面积是(
)cm2
丙的面积是(
)cm2
16
25
甲的面积加上乙的面积等于丙的面积。
单位:cm
9
甲、乙、丙三个正方形的面积之间,有什么关系?
甲
乙
3
4
5
丙
=25cm2
9cm2+16cm2
S甲+S乙
=S丙
单位:cm
乙的面积是(
)cm2
甲的面积是(
)cm2
丙的面积是(
)cm2
16
25
9
甲
乙
a
b
c
丙
甲、乙、丙三个正方形的面积之间,有什么关系?
甲
乙
3
4
5
丙
=25cm2
9cm2+16cm2
S甲+S乙
=S丙
单位:cm
乙的面积是(
)cm2
甲的面积是(
)cm2
丙的面积是(
)cm2
16
25
9
以任意直角三角形的三条边分别为边长,向外做三个正方形,是否都能得到这种关系呢?
甲
乙
3
4
5
丙
S甲+S乙
=S丙
单位:cm
毕达哥拉斯树
单位:cm
甲
乙
丙
5.7
7.6
2.我们的发现:
1.填空:
甲的边长是(
)cm,S甲=(
)cm2
S甲+S乙=(
)+(
)=(
)cm2
乙的边长是(
)cm,S乙=(
)cm2
丙的边长是(
)cm,S丙=(
)cm2
9.5
丙
活动要求
(一)4人小组合作,1人报数据,2人用
计算器计算,确保计算的结果正确,还有1
人做记录。
(二)4人一起说一说你们的发现,再把它
记录下来。
单位:cm
甲
乙
丙
5.7
7.6
2.我们的发现:
1.填空:
甲的边长是(
)cm,S甲=(
)cm2
S甲+S乙=(
)+(
)=(
)cm2
乙的边长是(
)cm,S乙=(
)cm2
丙的边长是(
)cm,S丙=(
)cm2
9.5
丙
单位:cm
甲
乙
丙
5.7
7.6
2.我们的发现:
1.填空:
甲的边长是(
)cm,S甲=(
)cm2
S甲+S乙=(
)+(
)=(
)cm2
乙的边长是(
)cm,S乙=(
)cm2
丙的边长是(
)cm,S丙=(
)cm2
9.5
丙
5.7
32.49
7.6
57.76
9.5
90.25
32.49
57.76
90.25
S甲+S乙=S丙
单位:cm
2.我们的发现:
1.填空:
甲的边长是(
)cm,S甲=(
)cm2
S甲+S乙=(
)+(
)=(
)cm2
乙的边长是(
)cm,S乙=(
)cm2
丙的边长是(
)cm,S丙=(
)cm2
甲
乙
丙
1.3
8.4
8.5
丙
1.3
1.69
8.4
70.56
8.5
72.25
1.69
70.56
72.25
S甲+S乙=S丙
单位:cm
甲
乙
丙
16
30
2.我们的发现:
1.填空:
甲的边长是(
)cm,S甲=(
)cm2
S甲+S乙=(
)+(
)=(
)cm2
乙的边长是(
)cm,S乙=(
)cm2
丙的边长是(
)cm,S丙=(
)cm2
34
丙
16
256
30
900
34
1156
256
900
1156
S甲+S乙=S丙
单位:cm
甲
乙
丙
3.3
5.6
2.我们的发现:
1.填空:
甲的边长是(
)cm,S甲=(
)cm2
S甲+S乙=(
)+(
)=(
)cm2
乙的边长是(
)cm,S乙=(
)cm2
丙的边长是(
)cm,S丙=(
)cm2
6.5
丙
3.3
10.89
5.6
31.36
6.5
42.25
10.89
31.36
42.25
S甲+S乙=S丙
单位:cm
2.我们的发现:
1.填空:
甲的边长是(
)cm,S甲=(
)cm2
S甲+S乙=(
)+(
)=(
)cm2
乙的边长是(
)cm,S乙=(
)cm2
丙的边长是(
)cm,S丙=(
)cm2
甲
乙
丙
1.1
6
6.1
丙
1.1
1.21
6
36
6.1
37.21
1.21
36
37.21
S甲+S乙=S丙
S甲+S乙=S丙
S甲+S乙=S丙
S甲+S乙=S丙
虽然每一组研究的数据不一样,但是结论都一样。
S甲+S乙=S丙
一句话概括刚才所有的发现。
任意一个直角三角形的三
条边,向外分别作三个正方形,
都是甲的面积加上乙的面积等于
丙的面积。
甲
乙
丙
丙
甲
乙
a
b
c
丙
S甲+S乙=S丙
甲
乙
a
b
c
丙
a?+b?=c?
a、b、c之间,有什么关系?
=a?
S甲=a×a
=b?
S乙=b×b
=c?
S丙=c×c
S甲+S乙=S丙
甲
乙
a
b
c
丙
a
b
c
a?+b?=c?
它不仅是三个正方形的边长
之间的关系,还是直角三角形中
三条边之间的关系。
直角边
另一条直角边
斜边
在直角三角形中,两直角边的平方和才会等于斜边的平方。
a
b
c
一条直角边的平方加另一条直角
边的平方等于斜边的平方。
直角边
另一条直角边
斜边
a?+b?=c?,在直角三角形中表示什么意思?
两条直角边的平方和,等于
斜边的平方。
a
b
c
a?+b?=c?
钝角三角形和锐角三角形,是不是也存在这种关系?
提出一个问题,比解决问题更重要。
a
b
c
a?+b?=c?
钝角三角形和锐角三角形,是不是也存在这种关系?
C(12)
a(6)
b(8)
a2+b2=c2,在锐角三角形、钝角三角形中是否适用呢?
a(6)
b(8)
C(9)
单位:cm
适用,因为它们都是三角形,都有三条边。
不适用,因为直角三角形中有直角,而钝角三角形和锐角三角形它们没有,它们不一样。
a2+b2=(
)cm2
a2+b2
c2
>
c2=(
)cm2
a2+b2=c2,在锐角三角形、钝角三角形中是否适用呢?
a2=(
)cm2
b2=(
)cm2
a(6)
b(8)
C(9)
36
64
100
81
在锐角三角形中,a?+b?=c?不适用。
a2+b2=c2,在锐角三角形、钝角三角形中是否适用呢?
C(12)
a(6)
b(8)
a2+b2=(
)cm2
a2+b2
c2
<
c2=(
)cm2
a2=(
)cm2
b2=(
)cm2
36
64
100
144
a?+b?=c?,不适用于钝角三角形。
a?+b?=c?
在锐角三角形和钝角三角形中都不适用。
直角三角形所特有的三边关系。
a是6厘米,b是8厘米,要使a和b的夹角是90度,组成直角三角形,c会是(
)厘米。
C(?
)
a(6)
b(8)
10
a?+b?=6?+8?=100cm2
a?+b?=c?=100cm2
10×10=100
c=10cm
直角三角形的三边关系
毕达哥拉斯树
a
b
c
a?+b?=c?
在直角三角形中,两直角边的平方和
等于斜边的平方。
直角边
另一条直角边
斜边
a?+b?=c?
毕达哥拉斯定理
一天,毕达哥拉斯应邀到朋友家做客。
他无意间发现主人家地面上铺着一块块漂亮
的正方形地砖,地砖的图案深深吸引着他。
他发现这些大小如一的地砖排列是有规律的,
彼此间产生着某种数量关系。
他索性拿出笔在地砖上画起图形,经过无
数次的验证,他得到“在直角三角形中,两直
角边的平方和等于斜边的平方”这一数量关系
是成立的。为了庆祝自己的发现,他屠杀了
100头牛庆祝。后来人们为了纪念他,把他的
发现叫做“毕达格拉斯定理”,也叫“百牛定
理”。
毕达哥拉斯树
毕达哥拉斯树
毕达哥拉斯定理
毕达哥拉斯定理,在中国叫做勾
股定理。早在3000多年前,我国数学
家商高就提出“勾三、股四、弦五”
的说法,我国就称它为“勾股定理”,
又叫“商高定理”。
3
4
5
再见!
