五年级数学上册课件 - 掷一掷 -人教版(共50张PPT)
文档属性
| 名称 | 五年级数学上册课件 - 掷一掷 -人教版(共50张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 12:56:29 | ||
图片预览










文档简介
掷一掷
掷一次骰子,掷出去朝上的点数,有几种可能?
六种的可能性,是一样的。
骰子
掷到1、2、3算老师赢;掷到4、5、6算同学们赢。
朝上的点数是1、2、5、6,算老师赢。剩下的点数,算同学们赢。
老师占了四个点数,同学们只有两个点数。
把六种点数进行平均分,使得点数相等。
游戏就公平。
掷一掷
掷一掷
两个骰子的点数之和,最大可能是几?
12
因为每个骰子最大的点数是6。
两个骰子加起来最大的点数:
6+6=12
两个骰子的点数之和,最小可能是几?
2
一个骰子最小的点数是1。
两个骰子最小的点数合在一起:
1+1=2
同时投掷两个骰子,朝上的点数之和,可能是几?
2、3、4、5、6、7、8、9、10、11、12
同时投掷两个骰子,朝上的点数之和,有多少种可能?
2、3、4、5、6、7、8、9、10、11、12
十一种可能
2、3、4、5、6、7、8、9、10、11、12
掷两个骰子,点数之和是2、3、4、10、11、12算同学们赢;点数之和是5、6、7、8、9,算老师赢。各掷10次,出现次数多者胜。
游戏规则
学生:
老师:
1
0
学生:
老师:
2
0
学生:
老师:
2
1
学生:
老师:
2
2
学生:
老师:
2
3
学生:
老师:
2
4
学生:
老师:
2
5
学生:
老师:
2
6
学生:
老师:
2
7
学生:
老师:
2
8
学生:
老师:
2
9
学生:
老师:
2
10
学生:
老师:
2
11
学生:
老师:
3
11
学生:
老师:
4
11
学生:
老师:
4
12
学生:
老师:
4
13
学生:
老师:
4
14
学生:
老师:
4
15
学生:
老师:
4
16
1.同桌两人掷骰子;
2.每人15次,共掷30次;
3.一个掷,一个完成统计表;
4.同桌两人交流自己的发现。
游戏规则
2
3
4
5
6
7
8
9
10
11
12
0
1
3
6
4
2
4
2
2
5
1
0
0
5
5
3
4
2
6
2
2
1
1
1
2
3
5
5
4
2
4
1
2
0
2
8
6
4
0
3
4
2
1
0
1
1
2
3
4
5
7
3
2
2
0
2
2
2
1
2
2
5
6
4
3
1
1
1
2
3
6
2
6
2
3
2
2
0
1
1
3
7
4
3
6
2
2
1
0
1
6
7
1
9
1
2
3
0
0
0
3
2
3
4
5
1
4
4
2
2
2
3
4
5
6
7
8
9
10
11
12
0
1
3
6
4
2
4
2
2
5
1
0
0
5
5
3
4
2
6
2
2
1
1
1
2
3
5
5
4
2
4
1
2
0
2
8
6
4
0
3
4
2
1
0
1
1
2
3
4
5
7
3
2
2
0
2
2
2
1
2
2
5
6
4
3
1
1
1
2
3
6
2
6
2
3
2
2
0
1
1
3
7
4
3
6
2
2
1
0
1
6
7
1
9
1
2
3
0
0
0
3
2
3
4
5
1
4
4
2
2
5
13
33
40
40
38
36
37
28
20
10
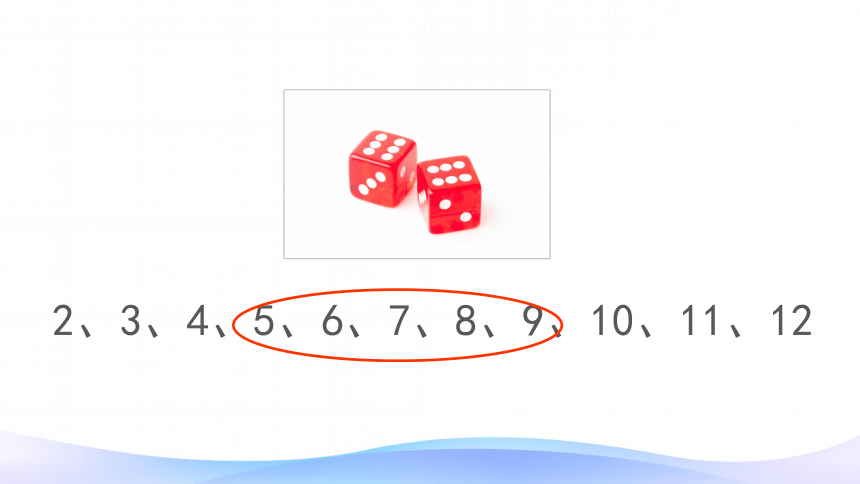
5、6、7、8、9的骰子点数特别多。
2、3、4、10、11、12,出现的可能性比较小。
2和12出现的可能性,最小。
要想胜出的几率高一些,应该选哪一组?
出现的可能性比较大,赢的可能性也要大一些。
3
4
5
6
7
8
9
10
11
12
为什么掷两个骰子,朝上的点数和是5、6、7、8、9,出现的可能性大一些?
点数之和5、6、7、8、9是由什么点数组成。
7:
1+6
2+5
3+4
2和12它出现的组合是最少的。
2只有1+1这一种可能,12只有6+6这一种可能。
点数之和是3的组合有两种,一种是1+2,一种是2+1。
1+2和2+1,是2种情况。
2
3
4
5
6
7
8
9
10
11
12
1+1
1+2
1+3
1+4
1+5
1+6
2+6
3+6
4+6
5+6
6+6
2+1
2+2
2+3
2+4
2+5
3+5
4+5
5+5
6+5
3+1
3+2
3+3
3+4
4+4
5+4
6+4
4+1
4+2
4+3
5+3
6+3
5+1
5+2
6+2
6+1
和
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1+2+3+4+5+6+5+4+3+2+1=36种
1+1
1+2
1+3
1+4
1+5
1+6
2+6
3+6
4+6
5+6
2
3
4
5
6
7
8
9
10
11
12
6+6
2+1
2+2
3+1
2+3
3+3
4+1
2+4
3+3
4+2
5+1
2+5
3+4
4+3
5+2
6+1
3+5
4+4
5+3
6+2
4+5
5+4
6+3
5+5
6+4
6+5
1+1
1+2
1+3
1+4
1+5
1+6
2+6
3+6
4+6
5+6
2
3
4
5
6
7
8
9
10
11
12
6+6
2+1
2+2
3+1
2+3
3+3
4+1
2+4
3+3
4+2
5+1
2+5
3+4
4+3
5+2
6+1
3+5
4+4
5+3
6+2
4+5
5+4
6+3
5+5
6+4
6+5
24
12
36
通过实验验证,发现规律,找到了规律背后的原因。
实验1000次“两个骰子之和”的出现情况统计图
2 3
5
50
100
125
次数
8 9 10
4 5
6 7
11 12
1713年,雅各布·伯努利的名著《猜度术》出版,这是概率论成为数学中的一个独立分支的标志。
掷骰子
抛硬币
抽扑克牌
轮盘游戏
随机信息
某商场举行一次摸奖活动,活动是这样的:消费一定金额
可以得到一次掷骰子的机会,将两个骰子同时掷出,得到的点数之和,如果是下列几种情况,就可以得到相应的奖品:
对于这样的摸奖活动,你们能用今天学到的知识揭开商家的秘密吗?
1? 特等奖? ?奖品为组合家电一套价值10000元。
2或12? 一等奖?? 奖品为一个电饭煲价值350元。
3或11? 二等奖?? 奖品为一壶油价值60元。
4或10? 三等奖?? 奖品为一瓶饮料价值3元。
5或9?? 鼓励奖?? 奖品为一支笔1元。
绝对不会出现两个骰子点数之和是1。
商家的秘密是不会有特等奖。
两个骰子最少的骰子点数是1,两个1加在一起是:1+1=2,2比1大。
1? 特等奖? ?奖品为组合家电一套价值10000元。
2或12? 一等奖?? 奖品为一个电饭煲价值350元。
3或11? 二等奖?? 奖品为一壶油价值60元。
4或10? 三等奖?? 奖品为一瓶饮料价值3元。
5或9?? 鼓励奖?? 奖品为一支笔1元。
某商场举行一次摸奖活动,活动是这样的:消费一定金额
可以得到一次掷骰子的机会,将两个骰子同时掷出,得到的点数之和如果是下列几种情况,就可以得到相应的奖品:
对于这样的摸奖活动,你们能用今天学到的知识揭开商家的秘密吗?
5或9的鼓励奖,奖励最小,因为它掷出的可能性是最大的。
掷出的点数和的可能性最大的时候,
奖品是最小的。
掷的可能性比较小的,奖品比较贵重一些。
掷出的可能性比较大的,反而奖品比较小。
看似公平的一些现象,背后隐藏着不公平的原理。
灵活运用自己学习的知识,解决问题。
研究了两个骰子之和,是5、6、7、8、9,为什么能出现那么多次?
通过猜想实验,我们还得到了结论。
看似公平的现象后面,存在着一定的数学原理。
再见!
掷一次骰子,掷出去朝上的点数,有几种可能?
六种的可能性,是一样的。
骰子
掷到1、2、3算老师赢;掷到4、5、6算同学们赢。
朝上的点数是1、2、5、6,算老师赢。剩下的点数,算同学们赢。
老师占了四个点数,同学们只有两个点数。
把六种点数进行平均分,使得点数相等。
游戏就公平。
掷一掷
掷一掷
两个骰子的点数之和,最大可能是几?
12
因为每个骰子最大的点数是6。
两个骰子加起来最大的点数:
6+6=12
两个骰子的点数之和,最小可能是几?
2
一个骰子最小的点数是1。
两个骰子最小的点数合在一起:
1+1=2
同时投掷两个骰子,朝上的点数之和,可能是几?
2、3、4、5、6、7、8、9、10、11、12
同时投掷两个骰子,朝上的点数之和,有多少种可能?
2、3、4、5、6、7、8、9、10、11、12
十一种可能
2、3、4、5、6、7、8、9、10、11、12
掷两个骰子,点数之和是2、3、4、10、11、12算同学们赢;点数之和是5、6、7、8、9,算老师赢。各掷10次,出现次数多者胜。
游戏规则
学生:
老师:
1
0
学生:
老师:
2
0
学生:
老师:
2
1
学生:
老师:
2
2
学生:
老师:
2
3
学生:
老师:
2
4
学生:
老师:
2
5
学生:
老师:
2
6
学生:
老师:
2
7
学生:
老师:
2
8
学生:
老师:
2
9
学生:
老师:
2
10
学生:
老师:
2
11
学生:
老师:
3
11
学生:
老师:
4
11
学生:
老师:
4
12
学生:
老师:
4
13
学生:
老师:
4
14
学生:
老师:
4
15
学生:
老师:
4
16
1.同桌两人掷骰子;
2.每人15次,共掷30次;
3.一个掷,一个完成统计表;
4.同桌两人交流自己的发现。
游戏规则
2
3
4
5
6
7
8
9
10
11
12
0
1
3
6
4
2
4
2
2
5
1
0
0
5
5
3
4
2
6
2
2
1
1
1
2
3
5
5
4
2
4
1
2
0
2
8
6
4
0
3
4
2
1
0
1
1
2
3
4
5
7
3
2
2
0
2
2
2
1
2
2
5
6
4
3
1
1
1
2
3
6
2
6
2
3
2
2
0
1
1
3
7
4
3
6
2
2
1
0
1
6
7
1
9
1
2
3
0
0
0
3
2
3
4
5
1
4
4
2
2
2
3
4
5
6
7
8
9
10
11
12
0
1
3
6
4
2
4
2
2
5
1
0
0
5
5
3
4
2
6
2
2
1
1
1
2
3
5
5
4
2
4
1
2
0
2
8
6
4
0
3
4
2
1
0
1
1
2
3
4
5
7
3
2
2
0
2
2
2
1
2
2
5
6
4
3
1
1
1
2
3
6
2
6
2
3
2
2
0
1
1
3
7
4
3
6
2
2
1
0
1
6
7
1
9
1
2
3
0
0
0
3
2
3
4
5
1
4
4
2
2
5
13
33
40
40
38
36
37
28
20
10
5、6、7、8、9的骰子点数特别多。
2、3、4、10、11、12,出现的可能性比较小。
2和12出现的可能性,最小。
要想胜出的几率高一些,应该选哪一组?
出现的可能性比较大,赢的可能性也要大一些。
3
4
5
6
7
8
9
10
11
12
为什么掷两个骰子,朝上的点数和是5、6、7、8、9,出现的可能性大一些?
点数之和5、6、7、8、9是由什么点数组成。
7:
1+6
2+5
3+4
2和12它出现的组合是最少的。
2只有1+1这一种可能,12只有6+6这一种可能。
点数之和是3的组合有两种,一种是1+2,一种是2+1。
1+2和2+1,是2种情况。
2
3
4
5
6
7
8
9
10
11
12
1+1
1+2
1+3
1+4
1+5
1+6
2+6
3+6
4+6
5+6
6+6
2+1
2+2
2+3
2+4
2+5
3+5
4+5
5+5
6+5
3+1
3+2
3+3
3+4
4+4
5+4
6+4
4+1
4+2
4+3
5+3
6+3
5+1
5+2
6+2
6+1
和
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
1+2+3+4+5+6+5+4+3+2+1=36种
1+1
1+2
1+3
1+4
1+5
1+6
2+6
3+6
4+6
5+6
2
3
4
5
6
7
8
9
10
11
12
6+6
2+1
2+2
3+1
2+3
3+3
4+1
2+4
3+3
4+2
5+1
2+5
3+4
4+3
5+2
6+1
3+5
4+4
5+3
6+2
4+5
5+4
6+3
5+5
6+4
6+5
1+1
1+2
1+3
1+4
1+5
1+6
2+6
3+6
4+6
5+6
2
3
4
5
6
7
8
9
10
11
12
6+6
2+1
2+2
3+1
2+3
3+3
4+1
2+4
3+3
4+2
5+1
2+5
3+4
4+3
5+2
6+1
3+5
4+4
5+3
6+2
4+5
5+4
6+3
5+5
6+4
6+5
24
12
36
通过实验验证,发现规律,找到了规律背后的原因。
实验1000次“两个骰子之和”的出现情况统计图
2 3
5
50
100
125
次数
8 9 10
4 5
6 7
11 12
1713年,雅各布·伯努利的名著《猜度术》出版,这是概率论成为数学中的一个独立分支的标志。
掷骰子
抛硬币
抽扑克牌
轮盘游戏
随机信息
某商场举行一次摸奖活动,活动是这样的:消费一定金额
可以得到一次掷骰子的机会,将两个骰子同时掷出,得到的点数之和,如果是下列几种情况,就可以得到相应的奖品:
对于这样的摸奖活动,你们能用今天学到的知识揭开商家的秘密吗?
1? 特等奖? ?奖品为组合家电一套价值10000元。
2或12? 一等奖?? 奖品为一个电饭煲价值350元。
3或11? 二等奖?? 奖品为一壶油价值60元。
4或10? 三等奖?? 奖品为一瓶饮料价值3元。
5或9?? 鼓励奖?? 奖品为一支笔1元。
绝对不会出现两个骰子点数之和是1。
商家的秘密是不会有特等奖。
两个骰子最少的骰子点数是1,两个1加在一起是:1+1=2,2比1大。
1? 特等奖? ?奖品为组合家电一套价值10000元。
2或12? 一等奖?? 奖品为一个电饭煲价值350元。
3或11? 二等奖?? 奖品为一壶油价值60元。
4或10? 三等奖?? 奖品为一瓶饮料价值3元。
5或9?? 鼓励奖?? 奖品为一支笔1元。
某商场举行一次摸奖活动,活动是这样的:消费一定金额
可以得到一次掷骰子的机会,将两个骰子同时掷出,得到的点数之和如果是下列几种情况,就可以得到相应的奖品:
对于这样的摸奖活动,你们能用今天学到的知识揭开商家的秘密吗?
5或9的鼓励奖,奖励最小,因为它掷出的可能性是最大的。
掷出的点数和的可能性最大的时候,
奖品是最小的。
掷的可能性比较小的,奖品比较贵重一些。
掷出的可能性比较大的,反而奖品比较小。
看似公平的一些现象,背后隐藏着不公平的原理。
灵活运用自己学习的知识,解决问题。
研究了两个骰子之和,是5、6、7、8、9,为什么能出现那么多次?
通过猜想实验,我们还得到了结论。
看似公平的现象后面,存在着一定的数学原理。
再见!
