北师大版九年级数学下册第一章1.1锐角三角函数 同步测试(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学下册第一章1.1锐角三角函数 同步测试(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 122.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 15:32:53 | ||
图片预览



文档简介
1144270010934700北师大版九年级数学下册第一章1.1锐角三角函数 同步测试
一.选择题
1.在Rt△ABC中,∠C=90°,AB=5,AC=3,则下列等式正确的是( )
A.sinA= B.cosA= C.tanA= D.cosA=
2. 如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( )
A.false B. false C.false D.false
若0?<α<90?,则下列说法不正确的是( )
A.sinα随α的增大而增大 B.cosα随α的增大而减小
C.tanα随α的增大而增大 D.sinα、cosα、tanα的值都随α的增大而增大
4.如图,在Rt△ABC中,∠A=90°,sinB=,AC=2,则BC长为( )
A.2 B.4 C.6 D.8
5. 已知sin6°=a,sin36°=b,则sin26°=( )
A.a2 B.2a C.b2 D.b
6.比较tan46?,cos29?,sin59?的大小关系是( )
A.tan46?C.sin59?7.已知在Rt△ABC中,∠C=90°,AC=,AB=4,则cosB的值是( )
A. B. C. D.
8. 在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,下列等式中不一定成立的是( )
A.b=atanB B.a=ccosB C.c=false D.a=bcosA
9.在Rt△ABC中,AC=8,BC=6,则cosA的值等于( )
A. B. C.或 D.或
10. 在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值( )
A.扩大2倍 B.缩小2倍 C.扩大4倍 D.没有变化
11.当锐角A的cosA>时,∠A的值为( )
A.小于45° B.小于30° C.大于45° D.大于30°
12. 当角度在0°到90°之间变化时,函数值随着角度的增大而增大的三角函数是( )
A.正弦和余弦 B.正弦和正切 C.余弦和正切 D.正弦、余弦和正切
二.填空题
13.在Rt△ABC中,∠C=90°,AB=4,BC=3,则sinA的值是 .
14. 如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB=_______________.
15. cos30?________?cos40?(填大小关系)
16.已知在△ABC中,AB=13,AC=12,∠C=90°,sinA= .
17. 比较下列三角函数值的大小:sin40°______cos40°(选填“>”、“=”、“<”)
18.已知在Rt△ABC中,∠C为直角,AC=4cm,BC=3cm,sin∠A=________. 19.比较大小:sin81° tan47°(填“<”、“=”或“>”).
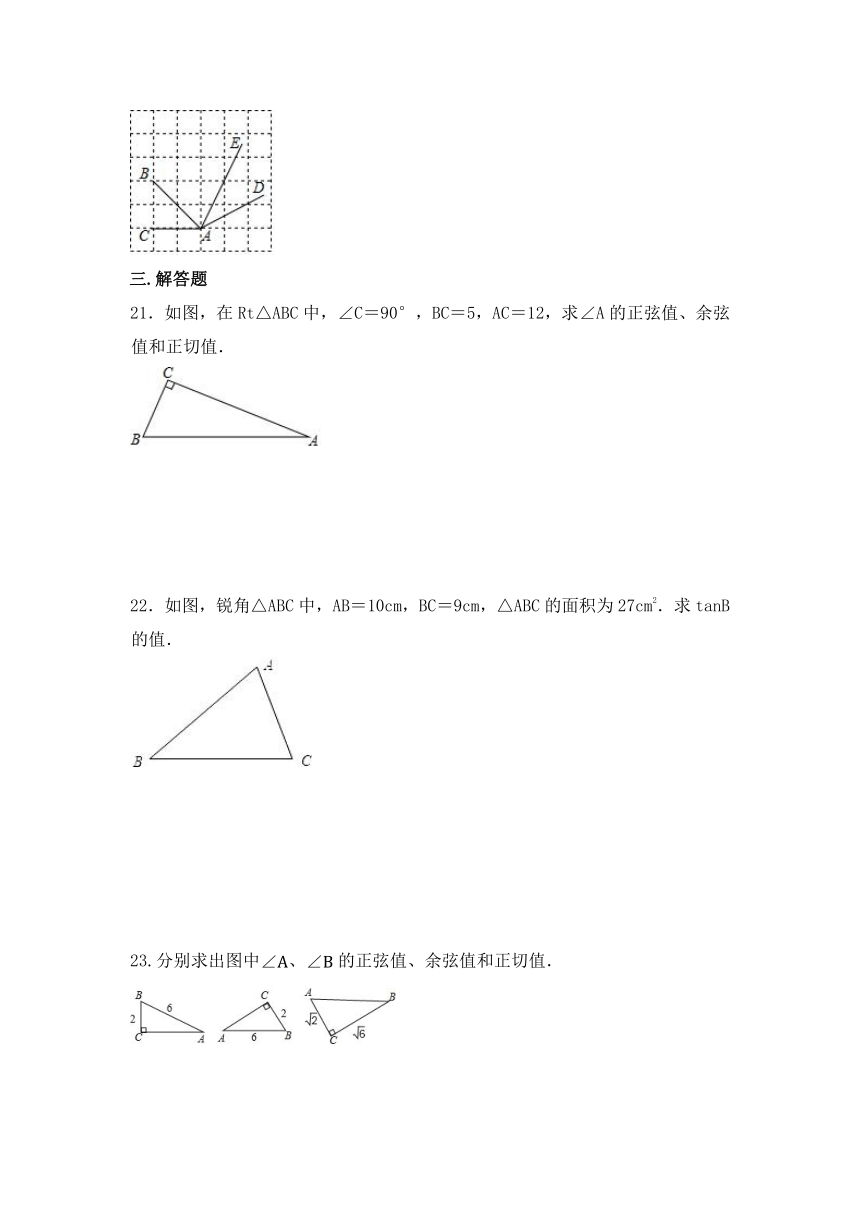
20.如图所示的网格是正方形网格,∠BAC ∠DAE.(填“>”,“=”或“<”)
三.解答题
21.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,求∠A的正弦值、余弦值和正切值.
22.如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2.求tanB的值.
23.分别求出图中∠A、∠B的正弦值、余弦值和正切值.
24.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,求∠ABC的正弦值
25.已知如图,A,B,C,D四点的坐标分别是(3,0),(0,4),(12,0),(0,9),探索∠OBA和∠OCD的大小关系,并说明理由.
26.在Rt△ABC中,∠ACB=90?,AC=3,tanB=43,求AB的值.
27.如图,在四边形ABCD中,BD平分∠ABC,∠BDC=∠A=90?,cos∠ABD=45,求S△ABDS△DBC的值.
28.(1)如图锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)根据你探索到的规律试比较18°,34°,50°,62°,88°,这些锐角的正弦值的大小和余弦值的大小.
(3)比较大小(在空格处填写“>”“=”“<”号),若α=45°,则sinα cosα;若0°<α<45°,则sinα cosα;若45°<α<90°,sinα cosα.
答案提示
1.B.2.D.3. D. 4.C.5.A.6. D.7.C.8.D.9.C.10.D.11.A.12.B.
13..14. false . 15. >.16..17.sin40°<cos40°.?18. 35 .19.<.20.=.
21.解:由勾股定理得,AB===13,
则sinA==,cosA==,tanA==.
22.解:过点A作AH⊥BC于H,
∵S△ABC=27,
∴,
∴AH=6,
∵AB=10,
∴BH===8,
∴tanB===.
23.解:如图1,AC=62-22=42,
sinA=26=13,
cosA=426=223,
tanA=242=24,
sinB=426=223,
cosB=26=13,
tanB=422=22.
如图2,AC=62-22=42,
sinA=26=13,
cosA=426=223,
tanA=242=24,
sinB=426=223,
cosB=26=13,
tanB=422=22.
如图3,AB=(2)2+(6)2=22,
sinA=622=32,
cosA=222=223,
tanA=62=3,
sinB=222=223,
cosB=622=32,
tanB=26=126=236=33.
24.解:AB2=32+12=10,BC2=22+12=5,AC=22+12=5,
∴AC=CB,BC2+AC2=AB2,
∴∠BCA=90°,
∴∠ABC=45°,
∴∠ABC的正弦值为false
25.解:∠OBA=∠OCD,理由如下:
由勾股定理,得
AB===5,CD===15,
sin∠OBA==,sin∠OCD===,
∠OBA=∠OCD.
26. 解:在Rt△ABC中,∠ACB=90?,AC=3,tanB=43,
∵tanB=ACBC,
∴BC=ACtanB=343=94,
则AB=AC2+BC2=154.
27. 解:∵BD平分∠ABC,∴∠ABD=∠DBC.
又∵∠BDC=∠A=90?,
∴△ABD∽△DBC.
∴S△ABDS△DBC=(ABBD)2,
在Rt△ABD中,∵cos∠ABD=ABBD=45,
∴S△ABDS△DBC=(45)2=1625.
28.解:(1)在图中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵sin∠B1AC=,sin∠B2AC=,sin∠B3AC=,
而>>,
∴sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图中,Rt△ACB3中,∠C=90°,
cos∠B1AC=,cos∠B2AC=,cos∠B3AC=,
∵AB3>AB2>AB1,
∴>>.
即cos∠B3AC<cos∠B2AC<cos∠B1AC;
结论:锐角的正弦值随角度的增大而增大,锐角的余弦值随角度的增大而减小.
(2)由(1)可知:
sin88°>sin62°>sin50°>sin34°>sin18°;
cos88°<cos62°<cos50°<cos34°<cos18°.
(3)若α=45°,则sinα=cosα;若0°<α<45°,则sinα<cosα;若45°<α<90°,则sinα>cosα.
故答案为:=,<,>.
一.选择题
1.在Rt△ABC中,∠C=90°,AB=5,AC=3,则下列等式正确的是( )
A.sinA= B.cosA= C.tanA= D.cosA=
2. 如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( )
A.false B. false C.false D.false
若0?<α<90?,则下列说法不正确的是( )
A.sinα随α的增大而增大 B.cosα随α的增大而减小
C.tanα随α的增大而增大 D.sinα、cosα、tanα的值都随α的增大而增大
4.如图,在Rt△ABC中,∠A=90°,sinB=,AC=2,则BC长为( )
A.2 B.4 C.6 D.8
5. 已知sin6°=a,sin36°=b,则sin26°=( )
A.a2 B.2a C.b2 D.b
6.比较tan46?,cos29?,sin59?的大小关系是( )
A.tan46?
A. B. C. D.
8. 在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,下列等式中不一定成立的是( )
A.b=atanB B.a=ccosB C.c=false D.a=bcosA
9.在Rt△ABC中,AC=8,BC=6,则cosA的值等于( )
A. B. C.或 D.或
10. 在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值( )
A.扩大2倍 B.缩小2倍 C.扩大4倍 D.没有变化
11.当锐角A的cosA>时,∠A的值为( )
A.小于45° B.小于30° C.大于45° D.大于30°
12. 当角度在0°到90°之间变化时,函数值随着角度的增大而增大的三角函数是( )
A.正弦和余弦 B.正弦和正切 C.余弦和正切 D.正弦、余弦和正切
二.填空题
13.在Rt△ABC中,∠C=90°,AB=4,BC=3,则sinA的值是 .
14. 如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB=_______________.
15. cos30?________?cos40?(填大小关系)
16.已知在△ABC中,AB=13,AC=12,∠C=90°,sinA= .
17. 比较下列三角函数值的大小:sin40°______cos40°(选填“>”、“=”、“<”)
18.已知在Rt△ABC中,∠C为直角,AC=4cm,BC=3cm,sin∠A=________. 19.比较大小:sin81° tan47°(填“<”、“=”或“>”).
20.如图所示的网格是正方形网格,∠BAC ∠DAE.(填“>”,“=”或“<”)
三.解答题
21.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,求∠A的正弦值、余弦值和正切值.
22.如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2.求tanB的值.
23.分别求出图中∠A、∠B的正弦值、余弦值和正切值.
24.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,求∠ABC的正弦值
25.已知如图,A,B,C,D四点的坐标分别是(3,0),(0,4),(12,0),(0,9),探索∠OBA和∠OCD的大小关系,并说明理由.
26.在Rt△ABC中,∠ACB=90?,AC=3,tanB=43,求AB的值.
27.如图,在四边形ABCD中,BD平分∠ABC,∠BDC=∠A=90?,cos∠ABD=45,求S△ABDS△DBC的值.
28.(1)如图锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)根据你探索到的规律试比较18°,34°,50°,62°,88°,这些锐角的正弦值的大小和余弦值的大小.
(3)比较大小(在空格处填写“>”“=”“<”号),若α=45°,则sinα cosα;若0°<α<45°,则sinα cosα;若45°<α<90°,sinα cosα.
答案提示
1.B.2.D.3. D. 4.C.5.A.6. D.7.C.8.D.9.C.10.D.11.A.12.B.
13..14. false . 15. >.16..17.sin40°<cos40°.?18. 35 .19.<.20.=.
21.解:由勾股定理得,AB===13,
则sinA==,cosA==,tanA==.
22.解:过点A作AH⊥BC于H,
∵S△ABC=27,
∴,
∴AH=6,
∵AB=10,
∴BH===8,
∴tanB===.
23.解:如图1,AC=62-22=42,
sinA=26=13,
cosA=426=223,
tanA=242=24,
sinB=426=223,
cosB=26=13,
tanB=422=22.
如图2,AC=62-22=42,
sinA=26=13,
cosA=426=223,
tanA=242=24,
sinB=426=223,
cosB=26=13,
tanB=422=22.
如图3,AB=(2)2+(6)2=22,
sinA=622=32,
cosA=222=223,
tanA=62=3,
sinB=222=223,
cosB=622=32,
tanB=26=126=236=33.
24.解:AB2=32+12=10,BC2=22+12=5,AC=22+12=5,
∴AC=CB,BC2+AC2=AB2,
∴∠BCA=90°,
∴∠ABC=45°,
∴∠ABC的正弦值为false
25.解:∠OBA=∠OCD,理由如下:
由勾股定理,得
AB===5,CD===15,
sin∠OBA==,sin∠OCD===,
∠OBA=∠OCD.
26. 解:在Rt△ABC中,∠ACB=90?,AC=3,tanB=43,
∵tanB=ACBC,
∴BC=ACtanB=343=94,
则AB=AC2+BC2=154.
27. 解:∵BD平分∠ABC,∴∠ABD=∠DBC.
又∵∠BDC=∠A=90?,
∴△ABD∽△DBC.
∴S△ABDS△DBC=(ABBD)2,
在Rt△ABD中,∵cos∠ABD=ABBD=45,
∴S△ABDS△DBC=(45)2=1625.
28.解:(1)在图中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵sin∠B1AC=,sin∠B2AC=,sin∠B3AC=,
而>>,
∴sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图中,Rt△ACB3中,∠C=90°,
cos∠B1AC=,cos∠B2AC=,cos∠B3AC=,
∵AB3>AB2>AB1,
∴>>.
即cos∠B3AC<cos∠B2AC<cos∠B1AC;
结论:锐角的正弦值随角度的增大而增大,锐角的余弦值随角度的增大而减小.
(2)由(1)可知:
sin88°>sin62°>sin50°>sin34°>sin18°;
cos88°<cos62°<cos50°<cos34°<cos18°.
(3)若α=45°,则sinα=cosα;若0°<α<45°,则sinα<cosα;若45°<α<90°,则sinα>cosα.
故答案为:=,<,>.
