苏科版八年级数学上册 第6章 一次函数 单元检测试题(word解析版)
文档属性
| 名称 | 苏科版八年级数学上册 第6章 一次函数 单元检测试题(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 168.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 19:18:08 | ||
图片预览




文档简介
第6章
一次函数
单元检测试题
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
?1.
某人加工个零件,若用表示工作效率,用表示时间,下列判断正确的是(?
?
?
?
)
A.和,都是常量
B.和都是变量
C.和都是变量
D.和都是变量
?2.
油箱中存油升,油从油箱中均匀流出,流速为升/分钟,则油箱中剩余油量(升)与流出时间(分钟)的函数关系是?
?
?
?
A.
B.
C.
D.
?
3.
如图所示,一次函数的图象经过、两点,则当时,的取值范围是(
)
A.
B.
C.
D.
?
4.
长方形的周长为,其中一条边为(其中),面积为,则在这个长方形中,与的关系可以写为(
)
A.
B.
C.
D.
?
5.
某学校计划用元钱买乒乓球,所购买球的个数(个)与单价(元)的关系式中(
)
A.是常量,,是变量
B.,是常量,是变量
C.,是常量,是变量
D.无法确定
?6.
观察函数和的图象,当,两个函数值的大小为(
)
A.
B.
C.
D.
?
7.
我校新建的自行车存放处每周的存车量为辆次,其中变速车存车费是每辆一次元,普通车存车费为每辆一次元.若普通存车量为辆次,存车的总收入为元,则与之间的关系式是(????????)
A.
B.
C.
D.
?
8.
下列函数中,与表示同一个函数的是(
)
A.
B.
C.
D.
?
9.
汽车由地驶往相距的地,它的平均速度是,则汽车距地路程与行驶时间的函数关系式及自变量的取值范围是(
)
A.??
B.??
C.??
D.??
?10.
药品研究所开发一种抗菌素新药,经过多年的动物实验之后,首次用于临床人体试验,测得成人服药后血液中药物浓度(微克/毫升)与服药后时间(时)之间的函数关系如图所示,则当时,的取值范围是(
)
A.
B.
C.
D.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
?
11.
已知自变量为的函数是正比例函数,则________,该函数的解析式为________.
?
12.
已知一次函数,当时,函数的值是________.
?
13.
函数:①;②;③④;⑤;⑥中,属一次函数的有________.(只填序号)
?
14.
根据一次函数的图象,当函数值大于零时,的范围是________.
?
15.
请写出符合下列性质的一个正比例函数,随的增大而减小.这个函数可以是________.
?
16.
画出一次函数的图象,并回答:当函数值为正时,的取值范围是________.
?
17.
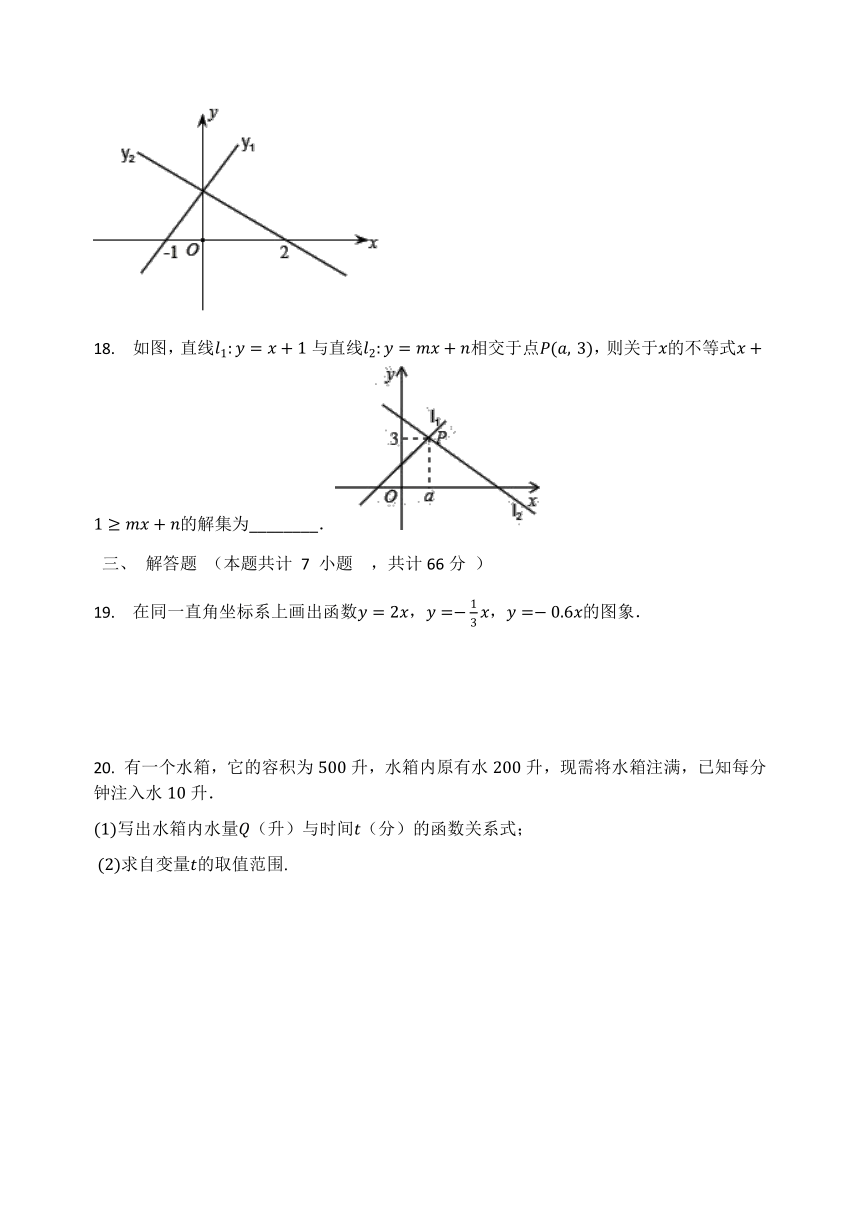
函数=与=的图象如图所示,这两个函数的交点在轴上,那么、的值都大于零的的取值范围是________.
18.
如图,直线与直线相交于点,则关于的不等式的解集为________.
三、
解答题
(本题共计
7
小题
,共计66分
)
?
19.
在同一直角坐标系上画出函数,,的图象.
?
20.
有一个水箱,它的容积为升,水箱内原有水升,现需将水箱注满,已知每分钟注入水升.
写出水箱内水量(升)与时间(分)的函数关系式;
求自变量的取值范围.
?
21.
某自行车保管站在某个星期日接受保管的自行车共有辆次,其中变速车保管费是每辆一次收元,一般车的保管费是每辆一次元,若一般车停放的辆次是,总的保管费为元,求与之间的函数关系式,并写出自变量的取值范围.
?
22.
暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人元的两家旅行社.经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按折收费;乙旅行社的优惠条件是:学生、家长都按折收费.假设这两位家长带领名学生去旅行,甲、乙旅行社的收费分别为,.
写出、与的函数关系式.
学生人数在什么情况下,选择哪个旅行社合算?
?
23.
如图,直线与直线相交于点.
求的值;
不解关于,的方程组请你直接写出它的解.
?
24.
如图,直线?与直线?相交于点,并且直线经过轴上点
(1)求直线的解析式.
(2)求两条直线与轴围成的三角形面积.
(3)直接写出不等式的解集.
?
25.
甲、乙两人相约元旦登山,甲、乙两人距地面的高度
与登山时间
之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
?________.
若乙提速后,乙登山的上升速度是甲登山的上升速度倍,
①则甲登山的上升速度是________;
②请求出甲登山过程中,距地面的高度
与登山时间
之间的函数关系式.
③当甲、乙两人距地面高度差为
时,求的值.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
C
【解答】
解:因为和都是可以取到不同的数值,所以是变量,
零件的个数是不变的量,是常量.
故选.
2.
【答案】
B
【解答】
解:由题意得,流出油量是,
则剩余油量.
故选.
3.
【答案】
C
【解答】
解:从图象上得到一次函数的图象经过,
又函数值随的增大而增大,
所以当时,.
故选.
4.
【答案】
B
【解答】
解:∵
长方形的周长为,其中一边为(其中),
∴
长方形的另一边长为,
∴
.
故选:.
5.
【答案】
A
【解答】
解:学校计划用元钱买乒乓球,所购买球的个数(个)与单价(元)的关系式,
是常量,,是变量,
故选:.
6.
【答案】
B
【解答】
解:当时,函数对应的点在函数对应点的上面,因而当,两个函数值的大小为
故选.
7.
【答案】
C
【解答】
略
8.
【答案】
D
【解答】
解:、不能为;
、不能为负数;
、不能为负数;
、正确.
故本题选.
9.
【答案】
A
【解答】
解:根据题意,得:,
∵
,
∴
,
∴
,
故选:.
10.
【答案】
C
【解答】
解:设当时,设,
∴
,
解得:,
∴
;
当时,设,
∴
,
解得:,
∴
,;
∴
当时,,当时,有最大值,当时,的值是,
所以当时,的取值范围是.
故选:.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
11.
【答案】
,
【解答】
解:∵
函数是正比例函数,
∴
,,
∴
,
该函数的解析式为.
故答案为:.
12.
【答案】
【解答】
解:把时代入一次函数,
得到:.
13.
【答案】
①②⑥
【解答】
解:①,是一次函数;
②,是一次函数;
③,自变量次数不为,故不是一次函数;
④,自变量次数不为,故不是一次函数;
⑤,自变量次数不为,故不是一次函数;
⑥,是一次函数.
属一次函数的有①②⑥.
故答案为:①②⑥.
14.
【答案】
【解答】
解:由函数可知,此函数与两坐标轴的交点分别为、,
由函数图象可知,当函数值大于零时,的范围是.
15.
【答案】
【解答】
解:随的增大而减小,则正比例系数是负数,则这个函数可以是:.
故答案是:(答案不唯一).
16.
【答案】
【解答】
解:当时,.
当时,.
则该直线经过点,.其图象如图所示:
根据图示知:当函数值为正时,的取值范围是:.
故答案是:.
17.
【答案】
【解答】
根据图示及数据可知,
函数=与轴的交点坐标是,
由图可知=与轴的交点坐标是,
所以、的值都大于零的的取值范围是:.
18.
【答案】
【解答】
解:把代入得:,
∴
,
∴
,
由图象可知:关于的不等式的解集是,
故答案为:.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
解:
【解答】
解:
20.
【答案】
解:根据题意,得:.
令,即,
解得.
【解答】
解:根据题意,得:.
令,即,
解得.
21.
【答案】
解:设一般车停放的辆次是,则变速车为:辆,
由题意得:,
整理得:.
【解答】
解:设一般车停放的辆次是,则变速车为:辆,
由题意得:,
整理得:.
22.
【答案】
解:由题意,得
,
;
所以、与的函数关系式分别为:
,.
当时,
,
解得:.
所以,当学生人数超过人时,选择甲旅行社更省钱,
当学生人数少于人时,选择乙旅行社更省钱,
当学生人数等于人时,选择甲、乙旅行社相等.
【解答】
解:由题意,得
,
;
所以、与的函数关系式分别为:
,.
当时,
,
解得:.
所以,当学生人数超过人时,选择甲旅行社更省钱,
当学生人数少于人时,选择乙旅行社更省钱,
当学生人数等于人时,选择甲、乙旅行社相等.
23.
【答案】
解:∵
在直线上,
∴
当时,.
因为,所以,
而两条直线相交于,
所以方程组的解是
【解答】
解:∵
在直线上,
∴
当时,.
因为,所以,
而两条直线相交于,
所以方程组的解是
24.
【答案】
解:(1)把代入中,得,
∴
,
∴
把,代入中得,
∴
,,
∴
一次函数的解析式是;
(2)设直线与轴交于点,则
∴
;
(3)不等式可以变形为,
结合图象得到解集为:.
【解答】
解:(1)把代入中,得,
∴
,
∴
把,代入中得,
∴
,,
∴
一次函数的解析式是;
(2)设直线与轴交于点,则
∴
;
(3)不等式可以变形为,
结合图象得到解集为:.
25.
【答案】
①以提速后的速度为:,
?甲的速度为?,
故答案为:;
②
甲登山用的时间为:?,
设甲登山过程中,距地面的高度??与登山时间??之间的
函数关系式为?,
则根据图象有:,解得?.
即所求函数关系式是;
③设乙在段对应的函数解析式为?,
由图象得,解得?,
?,
?),
解得??或?;
当?时,?,得?.
∴
当甲、乙两人距地面高度差为时,的值为或或
【解答】
解:在
段,乙每分钟走的路程为
米/分,
则
.
故答案为:;
①以提速后的速度为:,
甲的速度为
,
故答案为:;
②
甲登山用的时间为:
,
设甲登山过程中,距地面的高度
与登山时间
之间的
函数关系式为?,
则根据图象有:,解得?.
即所求函数关系式是;
③设乙在段对应的函数解析式为?,
由图象得,解得?,
?,
?),
解得??或?;
当?时,?,得?.
∴
当甲、乙两人距地面高度差为时,的值为或或.
一次函数
单元检测试题
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
?1.
某人加工个零件,若用表示工作效率,用表示时间,下列判断正确的是(?
?
?
?
)
A.和,都是常量
B.和都是变量
C.和都是变量
D.和都是变量
?2.
油箱中存油升,油从油箱中均匀流出,流速为升/分钟,则油箱中剩余油量(升)与流出时间(分钟)的函数关系是?
?
?
?
A.
B.
C.
D.
?
3.
如图所示,一次函数的图象经过、两点,则当时,的取值范围是(
)
A.
B.
C.
D.
?
4.
长方形的周长为,其中一条边为(其中),面积为,则在这个长方形中,与的关系可以写为(
)
A.
B.
C.
D.
?
5.
某学校计划用元钱买乒乓球,所购买球的个数(个)与单价(元)的关系式中(
)
A.是常量,,是变量
B.,是常量,是变量
C.,是常量,是变量
D.无法确定
?6.
观察函数和的图象,当,两个函数值的大小为(
)
A.
B.
C.
D.
?
7.
我校新建的自行车存放处每周的存车量为辆次,其中变速车存车费是每辆一次元,普通车存车费为每辆一次元.若普通存车量为辆次,存车的总收入为元,则与之间的关系式是(????????)
A.
B.
C.
D.
?
8.
下列函数中,与表示同一个函数的是(
)
A.
B.
C.
D.
?
9.
汽车由地驶往相距的地,它的平均速度是,则汽车距地路程与行驶时间的函数关系式及自变量的取值范围是(
)
A.??
B.??
C.??
D.??
?10.
药品研究所开发一种抗菌素新药,经过多年的动物实验之后,首次用于临床人体试验,测得成人服药后血液中药物浓度(微克/毫升)与服药后时间(时)之间的函数关系如图所示,则当时,的取值范围是(
)
A.
B.
C.
D.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
?
11.
已知自变量为的函数是正比例函数,则________,该函数的解析式为________.
?
12.
已知一次函数,当时,函数的值是________.
?
13.
函数:①;②;③④;⑤;⑥中,属一次函数的有________.(只填序号)
?
14.
根据一次函数的图象,当函数值大于零时,的范围是________.
?
15.
请写出符合下列性质的一个正比例函数,随的增大而减小.这个函数可以是________.
?
16.
画出一次函数的图象,并回答:当函数值为正时,的取值范围是________.
?
17.
函数=与=的图象如图所示,这两个函数的交点在轴上,那么、的值都大于零的的取值范围是________.
18.
如图,直线与直线相交于点,则关于的不等式的解集为________.
三、
解答题
(本题共计
7
小题
,共计66分
)
?
19.
在同一直角坐标系上画出函数,,的图象.
?
20.
有一个水箱,它的容积为升,水箱内原有水升,现需将水箱注满,已知每分钟注入水升.
写出水箱内水量(升)与时间(分)的函数关系式;
求自变量的取值范围.
?
21.
某自行车保管站在某个星期日接受保管的自行车共有辆次,其中变速车保管费是每辆一次收元,一般车的保管费是每辆一次元,若一般车停放的辆次是,总的保管费为元,求与之间的函数关系式,并写出自变量的取值范围.
?
22.
暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人元的两家旅行社.经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按折收费;乙旅行社的优惠条件是:学生、家长都按折收费.假设这两位家长带领名学生去旅行,甲、乙旅行社的收费分别为,.
写出、与的函数关系式.
学生人数在什么情况下,选择哪个旅行社合算?
?
23.
如图,直线与直线相交于点.
求的值;
不解关于,的方程组请你直接写出它的解.
?
24.
如图,直线?与直线?相交于点,并且直线经过轴上点
(1)求直线的解析式.
(2)求两条直线与轴围成的三角形面积.
(3)直接写出不等式的解集.
?
25.
甲、乙两人相约元旦登山,甲、乙两人距地面的高度
与登山时间
之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
?________.
若乙提速后,乙登山的上升速度是甲登山的上升速度倍,
①则甲登山的上升速度是________;
②请求出甲登山过程中,距地面的高度
与登山时间
之间的函数关系式.
③当甲、乙两人距地面高度差为
时,求的值.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
C
【解答】
解:因为和都是可以取到不同的数值,所以是变量,
零件的个数是不变的量,是常量.
故选.
2.
【答案】
B
【解答】
解:由题意得,流出油量是,
则剩余油量.
故选.
3.
【答案】
C
【解答】
解:从图象上得到一次函数的图象经过,
又函数值随的增大而增大,
所以当时,.
故选.
4.
【答案】
B
【解答】
解:∵
长方形的周长为,其中一边为(其中),
∴
长方形的另一边长为,
∴
.
故选:.
5.
【答案】
A
【解答】
解:学校计划用元钱买乒乓球,所购买球的个数(个)与单价(元)的关系式,
是常量,,是变量,
故选:.
6.
【答案】
B
【解答】
解:当时,函数对应的点在函数对应点的上面,因而当,两个函数值的大小为
故选.
7.
【答案】
C
【解答】
略
8.
【答案】
D
【解答】
解:、不能为;
、不能为负数;
、不能为负数;
、正确.
故本题选.
9.
【答案】
A
【解答】
解:根据题意,得:,
∵
,
∴
,
∴
,
故选:.
10.
【答案】
C
【解答】
解:设当时,设,
∴
,
解得:,
∴
;
当时,设,
∴
,
解得:,
∴
,;
∴
当时,,当时,有最大值,当时,的值是,
所以当时,的取值范围是.
故选:.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
11.
【答案】
,
【解答】
解:∵
函数是正比例函数,
∴
,,
∴
,
该函数的解析式为.
故答案为:.
12.
【答案】
【解答】
解:把时代入一次函数,
得到:.
13.
【答案】
①②⑥
【解答】
解:①,是一次函数;
②,是一次函数;
③,自变量次数不为,故不是一次函数;
④,自变量次数不为,故不是一次函数;
⑤,自变量次数不为,故不是一次函数;
⑥,是一次函数.
属一次函数的有①②⑥.
故答案为:①②⑥.
14.
【答案】
【解答】
解:由函数可知,此函数与两坐标轴的交点分别为、,
由函数图象可知,当函数值大于零时,的范围是.
15.
【答案】
【解答】
解:随的增大而减小,则正比例系数是负数,则这个函数可以是:.
故答案是:(答案不唯一).
16.
【答案】
【解答】
解:当时,.
当时,.
则该直线经过点,.其图象如图所示:
根据图示知:当函数值为正时,的取值范围是:.
故答案是:.
17.
【答案】
【解答】
根据图示及数据可知,
函数=与轴的交点坐标是,
由图可知=与轴的交点坐标是,
所以、的值都大于零的的取值范围是:.
18.
【答案】
【解答】
解:把代入得:,
∴
,
∴
,
由图象可知:关于的不等式的解集是,
故答案为:.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
解:
【解答】
解:
20.
【答案】
解:根据题意,得:.
令,即,
解得.
【解答】
解:根据题意,得:.
令,即,
解得.
21.
【答案】
解:设一般车停放的辆次是,则变速车为:辆,
由题意得:,
整理得:.
【解答】
解:设一般车停放的辆次是,则变速车为:辆,
由题意得:,
整理得:.
22.
【答案】
解:由题意,得
,
;
所以、与的函数关系式分别为:
,.
当时,
,
解得:.
所以,当学生人数超过人时,选择甲旅行社更省钱,
当学生人数少于人时,选择乙旅行社更省钱,
当学生人数等于人时,选择甲、乙旅行社相等.
【解答】
解:由题意,得
,
;
所以、与的函数关系式分别为:
,.
当时,
,
解得:.
所以,当学生人数超过人时,选择甲旅行社更省钱,
当学生人数少于人时,选择乙旅行社更省钱,
当学生人数等于人时,选择甲、乙旅行社相等.
23.
【答案】
解:∵
在直线上,
∴
当时,.
因为,所以,
而两条直线相交于,
所以方程组的解是
【解答】
解:∵
在直线上,
∴
当时,.
因为,所以,
而两条直线相交于,
所以方程组的解是
24.
【答案】
解:(1)把代入中,得,
∴
,
∴
把,代入中得,
∴
,,
∴
一次函数的解析式是;
(2)设直线与轴交于点,则
∴
;
(3)不等式可以变形为,
结合图象得到解集为:.
【解答】
解:(1)把代入中,得,
∴
,
∴
把,代入中得,
∴
,,
∴
一次函数的解析式是;
(2)设直线与轴交于点,则
∴
;
(3)不等式可以变形为,
结合图象得到解集为:.
25.
【答案】
①以提速后的速度为:,
?甲的速度为?,
故答案为:;
②
甲登山用的时间为:?,
设甲登山过程中,距地面的高度??与登山时间??之间的
函数关系式为?,
则根据图象有:,解得?.
即所求函数关系式是;
③设乙在段对应的函数解析式为?,
由图象得,解得?,
?,
?),
解得??或?;
当?时,?,得?.
∴
当甲、乙两人距地面高度差为时,的值为或或
【解答】
解:在
段,乙每分钟走的路程为
米/分,
则
.
故答案为:;
①以提速后的速度为:,
甲的速度为
,
故答案为:;
②
甲登山用的时间为:
,
设甲登山过程中,距地面的高度
与登山时间
之间的
函数关系式为?,
则根据图象有:,解得?.
即所求函数关系式是;
③设乙在段对应的函数解析式为?,
由图象得,解得?,
?,
?),
解得??或?;
当?时,?,得?.
∴
当甲、乙两人距地面高度差为时,的值为或或.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
