人教版八年级上册11.1 与三角形有关的线段讲义(含答案)
文档属性
| 名称 | 人教版八年级上册11.1 与三角形有关的线段讲义(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 851.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 00:00:00 | ||
图片预览




文档简介
三角形的边
知识精讲:
1.
按边分类
?
?
2.
三边关系
三角形任意两边的和大于第三边;三角形任意两边的差小于第三边
???
3.
稳定性
如果三角形的三条边固定,那么三角形的形状和大小就完全确定了,三角形的这个特征叫做三角形的稳定性.除了三角形外,其他多边形不具备稳定性,因此在生产建设中,为达到巩固的目的,把一些构件都做成三角形结构.
三点剖析:
考点:1.
按边分类;2.三边关系;3.
稳定性
重难点:1.
在应用三边关系判断能否组成三角形时,可以简化为:当三条线段中最长的线段小于另两条线段之和时,或当三条线段中最短的线段大于另两条线段之差时,即可组成三角形.
2.
由三角形三边关系可得,如果a,
b,
c三条线段能够组成三角形,那么.
易错点:在做与三角形的边有关的计算时,最后一定要注意检验是否满足三边关系定理,即最终能否组成三角形.
题型讲解:
题模一:按边分类
例1.1.1
下列长度的三条线段能组成三角形的是(
)
A.1,2,3
B.1,,3
C.3,4,8
D.4,5,6
例1.1.2
下列说法中错误的是(
)
A.
三角形可分为锐角三角形、直角三角形和钝角三角形
B.
三角形可分为等腰三角形和等边三角形
C.
等腰三角形包括等边三角形
D.
斜三角形包括锐角三角形和钝角三角形
题模二:三边关系
例1.2.1
等腰三角形的周长是18cm,其中一边长为4cm,其它两边长分别为( )
A.4cm,10cm
B.7cm,7cm
C.4cm,10cm或7cm,7cm
D.无法确定
例1.2.2
如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为( )
A.5
B.6
C.7
D.10
例1.2.3
如图,已知是△的边上的高,是边上的中线,求证:
例1.2.4
小明和小丽是同班同学,小明的家距学校2千米远,小丽的家距学校5千米远,设小明家距小丽家x千米远,则x的值应满足(
)
A.
B.
C.或
D.
题模三:稳定性
例1.3.1
要使五边形木架(用五根根条钉成)不变形,至少要再钉上(
)根本条.
A.1
B.2
C.3
D.4
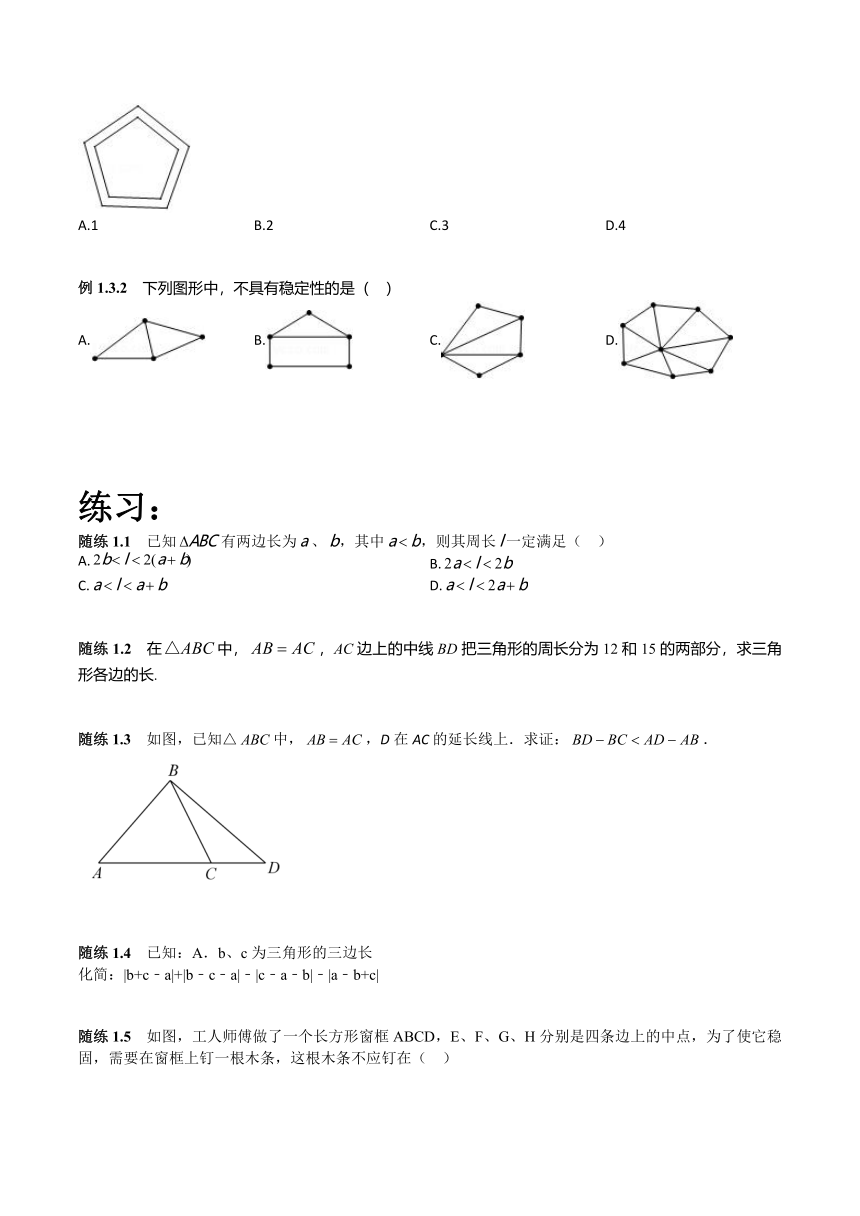
例1.3.2
下列图形中,不具有稳定性的是(
)
A.
B.
C.
D.
练习:
随练1.1
已知有两边长为、,其中,则其周长一定满足(
)
A.
B.
C.
D.
随练1.2
在中,,AC边上的中线BD把三角形的周长分为12和15的两部分,求三角形各边的长.
随练1.3
如图,已知△中,,D在AC的延长线上.求证:.
随练1.4
已知:A.b、c为三角形的三边长
化简:|b+c﹣a|+|b﹣c﹣a|﹣|c﹣a﹣b|﹣|a﹣b+c|
随练1.5
如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在(
)
A.A、C两点之间
B.E、G两点之间
C.B、F两点之间
D.G、H两点之间
三角形的高、中线、角平分线
知识点综合
1.
三角形的高、中线、角平分线
(1)从三角形的一个顶点向它的对边画垂线,顶点和垂足间的线段叫做三角形的高线;
(2)在三角形中,连结一个顶点和它的对边中点的线段叫做三角形的中线;
(3)每个三角形都有三条中线,且相交于一点,这个点叫做三角形的重心.
(4)三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线;
2.
面积问题
(1)解决面积相关的综合问题时,一般会用到等高三角形的面积比等于底之比,或者是同底三角形的面积比等于高之比.
(2)计算不规则的图形面积时,注意先把不规则的图形经过面积的加减组合,转化成容易计算的规则的图形面积,再进行计算.
三点剖析
考点:1.
三角形的高、中线、角平分线;2.
面积问题;
重难点:1.
锐角三角形的高均在三角形内部,三条高的交点也在三角形的内部;直角三角形两条高分别与两条直角边重合,三条高的交点也在三角形的直角顶点处;钝角三角形的高线中有两个垂足落在边的延长线上,这两条高落在三角形的外部.
2.
三角形三条中线的交点一定在三角形内部.
3.
每个三角形都有三条角平分线且交于一点,这个点叫三角形的内心,它也一定在三角形内部.
易错点:1.画三角形的高时,只要向对边或对边的延长线作垂线,连接顶点与垂足的线段就是该边的高.2.
三角形的角平分线是一条线段,而角的角平分线是一条射线.
题型讲解:
题模一:三角形的高、中线、角平分线
例2.1.1
如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A.
B.
C.
D.
例2.1.2
已知AD是△ABC的中线,则下列结论不正确的是(
)
A.
B.
C.
D.
例2.1.3
如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到,图中标出了点B的对应点.
(1)补全根据下列条件,利用网格点和三角板画图:
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)的面积为________
题模二:面积问题
例2.2.1
如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有____
A.2个
B.3个
C.4个
D.5个
例2.2.2
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于(
)
A.10
B.7
C.5
D.4
例2.2.3
(1)阅读下面材料并完成问题:
已知:直线AD与△ABC的边BC交于点D,
①如图1,当时,则S△ABD________S△ADC.(填“=”或“<”或“>”)
②如图2,当时,则S△ABD_____S△ADC.
③如图3,若AD∥BC,则有S△ABC____S△DBC.(填“=”或“<”或“>”)
(2)请你根据上述材料提供的信息,解决下列问题:
过四边形ABCD的一个顶点画一条直线,把四边形ABCD的面积分成的两部分.(保留画图痕迹)
题型练习:
随练2.1
如图,作出钝角△的边上的高.
随练2.2
如图的方格纸中,每个小方格都是边长为1的正方形,A、B两点是方格纸中的两个格点,在4×5的方格纸中,找出格点C,使△ABC的面积为1个平方单位,则满足条件的格点C的个数是
.
随练2.3
如图,对面积为1的逐次进行以下操作:第一次操作,分别延长、、至、、,使得,,,顺次连接、、,得到,记其面积为;第二次操作,分别延,,至,,,使得,,,顺次连接,,得到,记其面积为……,按此规律继续下去,可得到,则其面积为_________.
第次操作得到,则的面积
.
随练2.4
阅读下列材料:
某同学遇到这样一个问题:如图1,在中,,是的高.是边上一点,PM,PN分别与直线AB,AC垂直,垂足分别为点M,N.求证:.
他发现,连接AP,有,即.由,可得.
他又画出了当点在的延长线上,且上面问题中其他条件不变时的图形,如图2所示.他猜想此时BD,PM,PN之间的数量关系是:
请回答:
(1)请补全以下该同学证明猜想的过程;
∵___________,
∴___________,
∵,
∴.
(2)参考该同学思考问题的方法,解决下列问题:
在中,,BD是的高.P是所在平面上一点,PM,PN,PQ分别与直线AB,AC,BC垂直,垂足分别为点M,N,Q.
图3,若点P在的内部,则BD,PM,PN,PQ之间的数量关系是:_________________;
②若点P在如图4所示的位置,利用图4探究得出此时BD,PM,PN,PQ之间的数量关系是:________________________.
课后作业:
拓展1
等腰三角形的两边长分别是3和5,则这个等腰三角形的周长为
.
拓展2
有3cm,6cm,8cm,9cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为( )
A.1
B.2
C.3
D.4
拓展3
如图,中,已知,,则腰长的取值范围是(
)
A.
B.
C.
D.
拓展4
已知:a、b、c是△ABC三边长,且M=(a+b+c)(a+b-c)(a-b-c),那么(
)
A.M>0
B.M=0
C.M<0
D.不能确定
拓展5
如图1,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.则下列说法正确的是____
A.点M在AB上
B.点M在BC的中点处
C.点M在BC上,且距点B较近,距点C较远
D.点M在BC上,且距点C较近,距点B较远
拓展6
如图,△ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP长不可能是( )
A.2.5
B.3
C.4
D.5
拓展7
如图,在△ABC中,D是BA上一点,则成立吗?说明你的理由.
拓展8
在△ABC中,若AB=5,BC=2,且AC的长为奇数,则AC=________.
拓展9
如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在(
)
A.A、C两点之间
B.E、G两点之间
C.B、F两点之间
D.G、H两点之间
拓展10
能将三角形面积平分的是三角形的(
)
A.角平分线
B.高
C.中线
D.外角平分线
拓展11
如图,A、B、C分别是线段A1B,B1C,C1A的中点,若△ABC的面积是1,那么△A1B1C1的面积____.
拓展12
如图是阳光广告公司为某种商品设计的商标图案,图中阴影部分为红色。若每个小长方形的面积都是1,则红色的面积为________.
拓展13
如图,任意四边形ABCD中,AC和BD相交于点O,把△AOB、△AOD、△COD、△BOC的面积分别记作、、、,则下列各式成立的是(
)
A.
B.
C.
D.
拓展14
有一块三角形的优良品种实验土地,如图,现引进四个品种进行对比实验,须将这块土地分成面积相等的四块.请你制定出六种以上的划分方案.
拓展15
如图1,已知直线m∥n,点A、B在直线n上,点C、P在直线m上:(1)请写出图1中所有的面积相等的各对三角形:_____;(2)如图1,不难证明,点P在直线m上移动到任一位置时,总有△ABP与△ABC的面积相等;如图2,点M在△ABC的边上,请过点M画一条直线,平分△ABC的面积.(保留作图痕迹,并对作法做简要说明)
拓展16
如图,在△ABC中,E为AC的中点,点D为BC上一点,BD︰CD=2︰3,AD,BE交于点O,若S△AOE-S△BOD=1,则△ABC的面积为________.
答案解析
三角形的边
题模一:按边分类
例1.1.1
【答案】D
【解析】A、1+2=3,不能组成三角形,故本选项错误;
B、1+<3,不能组成三角形,故本选项错误;
C、3+4<8,不能组成三角形,故本选项错误;
D、4+5>6,能组成三角形,故本选项正确.
例1.1.2
【答案】B
【解析】三角形应该分为等腰三角形和不等边三角形.
题模二:三边关系
例1.2.1
【答案】B
【解析】当腰为4时,另一腰也为4,则底为18﹣2×4=10,
∵4+4=8<10,
∴这样的三边不能构成三角形.
当底为4时,腰为(18﹣4)÷2=7,
∵0<7<7+4=11,
∴以4,7,7为边能构成三角形.
故选B.
例1.2.2
【答案】C
【解析】此题实际考查的是三角形的三边关系定理,能够正确的判断出调整角度后三角形木框的组合方法是解答的关键.
若两个螺丝的距离最大,则此时这个木框的形状为三角形,可根据三条木棍的长来判断有几种三角形的组合,然后分别找出这些三角形的最长边即可.
已知4条木棍的四边长为2、3、4、6;
①选2+3、4、6作为三角形,则三边长为5、4、6;5-4<6<5+4,能构成三角形,此时两个螺丝间的最长距离为6;
②选3+4、6、2作为三角形,则三边长为2、7、6;6-2<7<6+2,能构成三角形,此时两个螺丝间的最大距离为7;
③选4+6、2、3作为三角形,则三边长为10、2、3;2+3<10,不能构成三角形,此种情况不成立;
④选6+2、3、4作为三角形,则三边长为8、3、4;而3+4<8,不能构成三角形,此种情况不成立;
综上所述,任两螺丝的距离之最大值为7.
故选:C.
例1.2.3
【答案】见解析
【解析】∵
∴,在△AEC中,.
又∵AE为中线,∴
即,∴
例1.2.4
【答案】D
【解析】该题考查的是三角形三边关系.
由题意可得,小明家可能在以学校为圆心,半径为2千米的圆上,小丽可能在以学校为圆心,
半径为5千米的圆上,
由图易得,
当两家处于A,B位置时距离最近,为千米,
当两家位于C,D位置时距离最远,为千米.
因此,x应当满足,
故答案为D.
题模三:稳定性
例1.3.1
【答案】B
【解析】如图,至少需要2根木条.
例1.3.2
【答案】B
【解析】本题考查的是三角形稳定性.
A可以看成两个三角形,而三角形具有稳定性,则这个图形一定具有稳定性,故本选项错误;
B可以看成一个三角形和一个四边形,而四边形不具有稳定性,则这个图形一定不具有稳定性,故本选项正确;
C可以看成三个三角形,而三角形具有稳定性,则这个图形一定具有稳定性,故本选项错误;
D可以看成7个三角形,而三角形具有稳定性,则这个图形一定具有稳定性,故本选项错误.
故选B.
随练1.1
【答案】A
【解析】设三角形的第三边长为x,由三角形的三边关系可知,.因此周长l满足
随练1.2
【答案】8,8,11或10,10,7
【解析】该题考查的是等腰三角形.
根据题意,①当15是腰长与腰长一半时,即,解得,
∴底边长是,此时三角形各边的长是10,10,7;
②当12是腰长与腰长一半时,即,解得,
∴底边长是,此时三角形各边的长是11,8,8.
随练1.3
【答案】见解析
【解析】∵在△中,
又∵∴
即
∴
随练1.4
【答案】2c-2a
【解析】∵A.b、c为三角形三边的长,
∴a+b>c,a+c>b,b+c>a,
∴原式=|(b+c)﹣a|+|b﹣(c+a)|﹣|c﹣(a+b)|﹣|(a+c)﹣b|
=b+c﹣a+a+c﹣b﹣a﹣b+c+b﹣a﹣c
=2c﹣2a.
随练1.5
【答案】B
【解析】工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.
三角形的高、中线、角平分线
题模一:三角形的高、中线、角平分线
例2.1.1
【答案】A
【解析】为△ABC中BC边上的高的是A选项.
例2.1.2
【答案】A
【解析】该题考察的是三角形中线的性质.
∵AD是△ABC的中线,
∴,B,C选项正确,
设h为点A到BC的垂线段长度
∵,
∴,D选项正确,
故答案是A.
例2.1.3
【答案】(1)如图所示:即为所求;
(2)如图所示:CD就是所求的中线;
(3)如图所示:AE即为BC边上的高;
(4)8.
【解析】(1)连接,过A、C分别做的平行线,并且在平行线上截取,顺次连接平移后各点,得到的三角形即为平移后的三角形;
(2)作AB的垂直平分线找到中点D,连接CD,CD就是所求的中线.
(3)从A点向BC的延长线作垂线,垂足为点E,AE即为BC边上的高;
(4).
故的面积为8.
题模二:面积问题
例2.2.1
【答案】B
【解析】
由图可知,AB∥x轴,且AB=3,
设点C到AB的距离为h,
则△ABC的面积=×3h=3,
解得h=2,
∵点C在第四象限,
∴点C的位置如图所示,共有3个.
故选:B.
例2.2.2
【答案】C
【解析】作EF⊥BC于F,
∵BE平分∠ABC,ED⊥AB,EF⊥BC,
∴EF=DE=2,
∴S△BCE=BC?EF=×5×2=5.
例2.2.3
【答案】(1)=;;(2)见解析
【解析】本题结合三角形的面积公式考查了作图-应用与设计作图.
用到的知识点:等底等高的两个三角形面积相等,等高的两个三角形面积之比等于对应底之比,两平行线之间的距离处处相等.
(1)①=--------------------------------------1分
②--------------------------------------2分
③=--------------------------------------3分
(2)方法一:
①过点D作DE∥AC交BC延长线于点E,
②F为BE三等分点
③则直线AF为所求,如图所示.
---------------------------5分
方法二:
①E为AC三等分点,
②过E作FG∥BD交DC于点E,BC于G,
③则直线DG为所求,如图所示.
---------------------------5分
随练2.1
【答案】如下图
【解析】根据三角形高线的定义,边上的高线应该交在延长线上
随练2.2
【答案】6
【解析】该题考查的是三角形的面积.
首先分别在AB的两侧找到一个使其面积是1个平方单位的点,
再分别过这两点作AB的平行线,找到所有的格点即可.
满足条件的C点有6个,如图平行于AB的直线上,与网格的所有交点就是.
随练2.3
【答案】;
【解析】本题考查的是三角形面积推理.
如图,连接,那么与的面积之比等于与的长度之比,为,
同理,与的面积之比为,那么的面积为面积的6倍;
同理,、的面积均为面积的6倍,
那么的面积为面积的19倍.
这样的操作进行次,得到的三角形面积为.
随练2.4
【答案】(1)见解析(2)①②
【解析】该题考查的是等面积方法的应用.
(1)由图可知
∵
∴,
∵
∴
(2)①连接AP、BP、CP
参考该同学思考问题的方法,则有
∵,
∴,
∵,
∴.
②过点P分别作直线AB,AC,BC的垂线P,垂足分别为点M,N,Q,
分别连接接AP、BP、CP,参考以上的思考方法,则有
∵,
∴,
∵,
∴.
拓展1
【答案】11或13.
【解析】①3是腰长时,三角形的三边分别为3、3、5,
能组成三角形,周长=3+3+5=11,
②3是底边长时,三角形的三边分别为3、5、5,
能组成三角形,周长=3+5+5=13,
综上所述,这个等腰三角形的周长是11或13.
故答案为:11或13.
拓展2
【答案】C
【解析】此题主要考查了三角形三边关系,三角形的三边关系:任意两边之和>第三边,任意两边之差<第三边;注意情况的多解和取舍.
从4条线段里任取3条线段组合,可有4种情况,看哪种情况不符合三角形三边关系,舍去即可.
四条木棒的所有组合:3,6,8和3,6,9和6,8,9和3,8,9;
只有3,6,8和6,8,9;3,8,9能组成三角形.
故选:C.
拓展3
【答案】B
【解析】根据三角形的三边关系定理来确定腰长x的取值范围.
若是等腰三角形,需满足的条件是:,解得
拓展4
【答案】C
【解析】∵a、b、c是△ABC三边长,
∴a+b+c>0,a+b-c>0,a-b-c<0,
∴M=(a+b+c)(a+b-c)(a-b-c).
拓展5
【答案】C
【解析】
解:∵∠C=100°,
∴AB>AC,
如图,取BC的中点E,则BE=CE,
∴AB+BE>AC+CE,
由三角形三边关系,AC+BC>AB,
∴AB<AD,
∴AD的中点M在BE上,
即点M在BC上,且距点B较近,距点C较远.
故选C.
拓展6
【答案】A
【解析】已知,在△ABC中,∠C=90°,AC=3,
根据垂线段最短,可知AP的长不可小于3,当P和C重合时,AP=3,
拓展7
【答案】见解析
【解析】∵在△中,
在△中,∴
∴
∴
拓展8
【答案】5
拓展9
【答案】B
【解析】工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.
拓展10
【答案】C
拓展11
【答案】7
【解析】
如图,连接AB1,BC1,CA1,
∵A、B分别是线段A1B,B1C的中点,
∴S△
ABB1=S△
ABC=1,
S△
A1AB1=S△
ABB1=1,
∴S△
A1BB1=S△
A1AB1+S△
ABB1=1+1=2,
同理:S△
B1CC1=2,S△
A1AC1=2,
∴△A1B1C1的面积=S△
A1BB1+S△
B1CC1+S△
A1AC1+S△
ABC=2+2+2+1=7.
故答案为:7.
拓展12
【答案】5
【解析】该题考察的是面积计算.
运用求差法:全部的面积减去空白的面积就是红色的面积.设小长方形长为2,宽为.
.
拓展13
【答案】D
【解析】该题考查的是面积问题.
在△ABC中,△AOB与△COB
同高,所以,同理可得,所以,所以,该题答案选D.
拓展14
【答案】见下图
【解析】三角形一边上的中线可以把三角形分成两个面积相等的小三角形,因此本题可以利用中线设计划分方案.
拓展15
【答案】(1),,(2)见解析
【解析】该题考查的是尺规作图.
(1)因为平行线间的距离相等,所以,,;
(2)连接MC;过AB中点D作DE//MC交BC于点E;作直线ME,ME为过点M平分三角形面积的直线.
拓展16
【答案】
【解析】∵点E为AC的中点,
∴S△ABE=S△ABC.
∵BD:CD=2:3,
∴S△ABD=S△ABC,
∵S△AOE-S△BOD=1,
∴S△ABE-S△ABD=S△ABC-S△ABC=1,
解得S△ABC=10.
故答案为:10
0
知识精讲:
1.
按边分类
?
?
2.
三边关系
三角形任意两边的和大于第三边;三角形任意两边的差小于第三边
???
3.
稳定性
如果三角形的三条边固定,那么三角形的形状和大小就完全确定了,三角形的这个特征叫做三角形的稳定性.除了三角形外,其他多边形不具备稳定性,因此在生产建设中,为达到巩固的目的,把一些构件都做成三角形结构.
三点剖析:
考点:1.
按边分类;2.三边关系;3.
稳定性
重难点:1.
在应用三边关系判断能否组成三角形时,可以简化为:当三条线段中最长的线段小于另两条线段之和时,或当三条线段中最短的线段大于另两条线段之差时,即可组成三角形.
2.
由三角形三边关系可得,如果a,
b,
c三条线段能够组成三角形,那么.
易错点:在做与三角形的边有关的计算时,最后一定要注意检验是否满足三边关系定理,即最终能否组成三角形.
题型讲解:
题模一:按边分类
例1.1.1
下列长度的三条线段能组成三角形的是(
)
A.1,2,3
B.1,,3
C.3,4,8
D.4,5,6
例1.1.2
下列说法中错误的是(
)
A.
三角形可分为锐角三角形、直角三角形和钝角三角形
B.
三角形可分为等腰三角形和等边三角形
C.
等腰三角形包括等边三角形
D.
斜三角形包括锐角三角形和钝角三角形
题模二:三边关系
例1.2.1
等腰三角形的周长是18cm,其中一边长为4cm,其它两边长分别为( )
A.4cm,10cm
B.7cm,7cm
C.4cm,10cm或7cm,7cm
D.无法确定
例1.2.2
如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为( )
A.5
B.6
C.7
D.10
例1.2.3
如图,已知是△的边上的高,是边上的中线,求证:
例1.2.4
小明和小丽是同班同学,小明的家距学校2千米远,小丽的家距学校5千米远,设小明家距小丽家x千米远,则x的值应满足(
)
A.
B.
C.或
D.
题模三:稳定性
例1.3.1
要使五边形木架(用五根根条钉成)不变形,至少要再钉上(
)根本条.
A.1
B.2
C.3
D.4
例1.3.2
下列图形中,不具有稳定性的是(
)
A.
B.
C.
D.
练习:
随练1.1
已知有两边长为、,其中,则其周长一定满足(
)
A.
B.
C.
D.
随练1.2
在中,,AC边上的中线BD把三角形的周长分为12和15的两部分,求三角形各边的长.
随练1.3
如图,已知△中,,D在AC的延长线上.求证:.
随练1.4
已知:A.b、c为三角形的三边长
化简:|b+c﹣a|+|b﹣c﹣a|﹣|c﹣a﹣b|﹣|a﹣b+c|
随练1.5
如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在(
)
A.A、C两点之间
B.E、G两点之间
C.B、F两点之间
D.G、H两点之间
三角形的高、中线、角平分线
知识点综合
1.
三角形的高、中线、角平分线
(1)从三角形的一个顶点向它的对边画垂线,顶点和垂足间的线段叫做三角形的高线;
(2)在三角形中,连结一个顶点和它的对边中点的线段叫做三角形的中线;
(3)每个三角形都有三条中线,且相交于一点,这个点叫做三角形的重心.
(4)三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线;
2.
面积问题
(1)解决面积相关的综合问题时,一般会用到等高三角形的面积比等于底之比,或者是同底三角形的面积比等于高之比.
(2)计算不规则的图形面积时,注意先把不规则的图形经过面积的加减组合,转化成容易计算的规则的图形面积,再进行计算.
三点剖析
考点:1.
三角形的高、中线、角平分线;2.
面积问题;
重难点:1.
锐角三角形的高均在三角形内部,三条高的交点也在三角形的内部;直角三角形两条高分别与两条直角边重合,三条高的交点也在三角形的直角顶点处;钝角三角形的高线中有两个垂足落在边的延长线上,这两条高落在三角形的外部.
2.
三角形三条中线的交点一定在三角形内部.
3.
每个三角形都有三条角平分线且交于一点,这个点叫三角形的内心,它也一定在三角形内部.
易错点:1.画三角形的高时,只要向对边或对边的延长线作垂线,连接顶点与垂足的线段就是该边的高.2.
三角形的角平分线是一条线段,而角的角平分线是一条射线.
题型讲解:
题模一:三角形的高、中线、角平分线
例2.1.1
如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A.
B.
C.
D.
例2.1.2
已知AD是△ABC的中线,则下列结论不正确的是(
)
A.
B.
C.
D.
例2.1.3
如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到,图中标出了点B的对应点.
(1)补全根据下列条件,利用网格点和三角板画图:
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)的面积为________
题模二:面积问题
例2.2.1
如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有____
A.2个
B.3个
C.4个
D.5个
例2.2.2
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于(
)
A.10
B.7
C.5
D.4
例2.2.3
(1)阅读下面材料并完成问题:
已知:直线AD与△ABC的边BC交于点D,
①如图1,当时,则S△ABD________S△ADC.(填“=”或“<”或“>”)
②如图2,当时,则S△ABD_____S△ADC.
③如图3,若AD∥BC,则有S△ABC____S△DBC.(填“=”或“<”或“>”)
(2)请你根据上述材料提供的信息,解决下列问题:
过四边形ABCD的一个顶点画一条直线,把四边形ABCD的面积分成的两部分.(保留画图痕迹)
题型练习:
随练2.1
如图,作出钝角△的边上的高.
随练2.2
如图的方格纸中,每个小方格都是边长为1的正方形,A、B两点是方格纸中的两个格点,在4×5的方格纸中,找出格点C,使△ABC的面积为1个平方单位,则满足条件的格点C的个数是
.
随练2.3
如图,对面积为1的逐次进行以下操作:第一次操作,分别延长、、至、、,使得,,,顺次连接、、,得到,记其面积为;第二次操作,分别延,,至,,,使得,,,顺次连接,,得到,记其面积为……,按此规律继续下去,可得到,则其面积为_________.
第次操作得到,则的面积
.
随练2.4
阅读下列材料:
某同学遇到这样一个问题:如图1,在中,,是的高.是边上一点,PM,PN分别与直线AB,AC垂直,垂足分别为点M,N.求证:.
他发现,连接AP,有,即.由,可得.
他又画出了当点在的延长线上,且上面问题中其他条件不变时的图形,如图2所示.他猜想此时BD,PM,PN之间的数量关系是:
请回答:
(1)请补全以下该同学证明猜想的过程;
∵___________,
∴___________,
∵,
∴.
(2)参考该同学思考问题的方法,解决下列问题:
在中,,BD是的高.P是所在平面上一点,PM,PN,PQ分别与直线AB,AC,BC垂直,垂足分别为点M,N,Q.
图3,若点P在的内部,则BD,PM,PN,PQ之间的数量关系是:_________________;
②若点P在如图4所示的位置,利用图4探究得出此时BD,PM,PN,PQ之间的数量关系是:________________________.
课后作业:
拓展1
等腰三角形的两边长分别是3和5,则这个等腰三角形的周长为
.
拓展2
有3cm,6cm,8cm,9cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为( )
A.1
B.2
C.3
D.4
拓展3
如图,中,已知,,则腰长的取值范围是(
)
A.
B.
C.
D.
拓展4
已知:a、b、c是△ABC三边长,且M=(a+b+c)(a+b-c)(a-b-c),那么(
)
A.M>0
B.M=0
C.M<0
D.不能确定
拓展5
如图1,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.则下列说法正确的是____
A.点M在AB上
B.点M在BC的中点处
C.点M在BC上,且距点B较近,距点C较远
D.点M在BC上,且距点C较近,距点B较远
拓展6
如图,△ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP长不可能是( )
A.2.5
B.3
C.4
D.5
拓展7
如图,在△ABC中,D是BA上一点,则成立吗?说明你的理由.
拓展8
在△ABC中,若AB=5,BC=2,且AC的长为奇数,则AC=________.
拓展9
如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在(
)
A.A、C两点之间
B.E、G两点之间
C.B、F两点之间
D.G、H两点之间
拓展10
能将三角形面积平分的是三角形的(
)
A.角平分线
B.高
C.中线
D.外角平分线
拓展11
如图,A、B、C分别是线段A1B,B1C,C1A的中点,若△ABC的面积是1,那么△A1B1C1的面积____.
拓展12
如图是阳光广告公司为某种商品设计的商标图案,图中阴影部分为红色。若每个小长方形的面积都是1,则红色的面积为________.
拓展13
如图,任意四边形ABCD中,AC和BD相交于点O,把△AOB、△AOD、△COD、△BOC的面积分别记作、、、,则下列各式成立的是(
)
A.
B.
C.
D.
拓展14
有一块三角形的优良品种实验土地,如图,现引进四个品种进行对比实验,须将这块土地分成面积相等的四块.请你制定出六种以上的划分方案.
拓展15
如图1,已知直线m∥n,点A、B在直线n上,点C、P在直线m上:(1)请写出图1中所有的面积相等的各对三角形:_____;(2)如图1,不难证明,点P在直线m上移动到任一位置时,总有△ABP与△ABC的面积相等;如图2,点M在△ABC的边上,请过点M画一条直线,平分△ABC的面积.(保留作图痕迹,并对作法做简要说明)
拓展16
如图,在△ABC中,E为AC的中点,点D为BC上一点,BD︰CD=2︰3,AD,BE交于点O,若S△AOE-S△BOD=1,则△ABC的面积为________.
答案解析
三角形的边
题模一:按边分类
例1.1.1
【答案】D
【解析】A、1+2=3,不能组成三角形,故本选项错误;
B、1+<3,不能组成三角形,故本选项错误;
C、3+4<8,不能组成三角形,故本选项错误;
D、4+5>6,能组成三角形,故本选项正确.
例1.1.2
【答案】B
【解析】三角形应该分为等腰三角形和不等边三角形.
题模二:三边关系
例1.2.1
【答案】B
【解析】当腰为4时,另一腰也为4,则底为18﹣2×4=10,
∵4+4=8<10,
∴这样的三边不能构成三角形.
当底为4时,腰为(18﹣4)÷2=7,
∵0<7<7+4=11,
∴以4,7,7为边能构成三角形.
故选B.
例1.2.2
【答案】C
【解析】此题实际考查的是三角形的三边关系定理,能够正确的判断出调整角度后三角形木框的组合方法是解答的关键.
若两个螺丝的距离最大,则此时这个木框的形状为三角形,可根据三条木棍的长来判断有几种三角形的组合,然后分别找出这些三角形的最长边即可.
已知4条木棍的四边长为2、3、4、6;
①选2+3、4、6作为三角形,则三边长为5、4、6;5-4<6<5+4,能构成三角形,此时两个螺丝间的最长距离为6;
②选3+4、6、2作为三角形,则三边长为2、7、6;6-2<7<6+2,能构成三角形,此时两个螺丝间的最大距离为7;
③选4+6、2、3作为三角形,则三边长为10、2、3;2+3<10,不能构成三角形,此种情况不成立;
④选6+2、3、4作为三角形,则三边长为8、3、4;而3+4<8,不能构成三角形,此种情况不成立;
综上所述,任两螺丝的距离之最大值为7.
故选:C.
例1.2.3
【答案】见解析
【解析】∵
∴,在△AEC中,.
又∵AE为中线,∴
即,∴
例1.2.4
【答案】D
【解析】该题考查的是三角形三边关系.
由题意可得,小明家可能在以学校为圆心,半径为2千米的圆上,小丽可能在以学校为圆心,
半径为5千米的圆上,
由图易得,
当两家处于A,B位置时距离最近,为千米,
当两家位于C,D位置时距离最远,为千米.
因此,x应当满足,
故答案为D.
题模三:稳定性
例1.3.1
【答案】B
【解析】如图,至少需要2根木条.
例1.3.2
【答案】B
【解析】本题考查的是三角形稳定性.
A可以看成两个三角形,而三角形具有稳定性,则这个图形一定具有稳定性,故本选项错误;
B可以看成一个三角形和一个四边形,而四边形不具有稳定性,则这个图形一定不具有稳定性,故本选项正确;
C可以看成三个三角形,而三角形具有稳定性,则这个图形一定具有稳定性,故本选项错误;
D可以看成7个三角形,而三角形具有稳定性,则这个图形一定具有稳定性,故本选项错误.
故选B.
随练1.1
【答案】A
【解析】设三角形的第三边长为x,由三角形的三边关系可知,.因此周长l满足
随练1.2
【答案】8,8,11或10,10,7
【解析】该题考查的是等腰三角形.
根据题意,①当15是腰长与腰长一半时,即,解得,
∴底边长是,此时三角形各边的长是10,10,7;
②当12是腰长与腰长一半时,即,解得,
∴底边长是,此时三角形各边的长是11,8,8.
随练1.3
【答案】见解析
【解析】∵在△中,
又∵∴
即
∴
随练1.4
【答案】2c-2a
【解析】∵A.b、c为三角形三边的长,
∴a+b>c,a+c>b,b+c>a,
∴原式=|(b+c)﹣a|+|b﹣(c+a)|﹣|c﹣(a+b)|﹣|(a+c)﹣b|
=b+c﹣a+a+c﹣b﹣a﹣b+c+b﹣a﹣c
=2c﹣2a.
随练1.5
【答案】B
【解析】工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.
三角形的高、中线、角平分线
题模一:三角形的高、中线、角平分线
例2.1.1
【答案】A
【解析】为△ABC中BC边上的高的是A选项.
例2.1.2
【答案】A
【解析】该题考察的是三角形中线的性质.
∵AD是△ABC的中线,
∴,B,C选项正确,
设h为点A到BC的垂线段长度
∵,
∴,D选项正确,
故答案是A.
例2.1.3
【答案】(1)如图所示:即为所求;
(2)如图所示:CD就是所求的中线;
(3)如图所示:AE即为BC边上的高;
(4)8.
【解析】(1)连接,过A、C分别做的平行线,并且在平行线上截取,顺次连接平移后各点,得到的三角形即为平移后的三角形;
(2)作AB的垂直平分线找到中点D,连接CD,CD就是所求的中线.
(3)从A点向BC的延长线作垂线,垂足为点E,AE即为BC边上的高;
(4).
故的面积为8.
题模二:面积问题
例2.2.1
【答案】B
【解析】
由图可知,AB∥x轴,且AB=3,
设点C到AB的距离为h,
则△ABC的面积=×3h=3,
解得h=2,
∵点C在第四象限,
∴点C的位置如图所示,共有3个.
故选:B.
例2.2.2
【答案】C
【解析】作EF⊥BC于F,
∵BE平分∠ABC,ED⊥AB,EF⊥BC,
∴EF=DE=2,
∴S△BCE=BC?EF=×5×2=5.
例2.2.3
【答案】(1)=;;(2)见解析
【解析】本题结合三角形的面积公式考查了作图-应用与设计作图.
用到的知识点:等底等高的两个三角形面积相等,等高的两个三角形面积之比等于对应底之比,两平行线之间的距离处处相等.
(1)①=--------------------------------------1分
②--------------------------------------2分
③=--------------------------------------3分
(2)方法一:
①过点D作DE∥AC交BC延长线于点E,
②F为BE三等分点
③则直线AF为所求,如图所示.
---------------------------5分
方法二:
①E为AC三等分点,
②过E作FG∥BD交DC于点E,BC于G,
③则直线DG为所求,如图所示.
---------------------------5分
随练2.1
【答案】如下图
【解析】根据三角形高线的定义,边上的高线应该交在延长线上
随练2.2
【答案】6
【解析】该题考查的是三角形的面积.
首先分别在AB的两侧找到一个使其面积是1个平方单位的点,
再分别过这两点作AB的平行线,找到所有的格点即可.
满足条件的C点有6个,如图平行于AB的直线上,与网格的所有交点就是.
随练2.3
【答案】;
【解析】本题考查的是三角形面积推理.
如图,连接,那么与的面积之比等于与的长度之比,为,
同理,与的面积之比为,那么的面积为面积的6倍;
同理,、的面积均为面积的6倍,
那么的面积为面积的19倍.
这样的操作进行次,得到的三角形面积为.
随练2.4
【答案】(1)见解析(2)①②
【解析】该题考查的是等面积方法的应用.
(1)由图可知
∵
∴,
∵
∴
(2)①连接AP、BP、CP
参考该同学思考问题的方法,则有
∵,
∴,
∵,
∴.
②过点P分别作直线AB,AC,BC的垂线P,垂足分别为点M,N,Q,
分别连接接AP、BP、CP,参考以上的思考方法,则有
∵,
∴,
∵,
∴.
拓展1
【答案】11或13.
【解析】①3是腰长时,三角形的三边分别为3、3、5,
能组成三角形,周长=3+3+5=11,
②3是底边长时,三角形的三边分别为3、5、5,
能组成三角形,周长=3+5+5=13,
综上所述,这个等腰三角形的周长是11或13.
故答案为:11或13.
拓展2
【答案】C
【解析】此题主要考查了三角形三边关系,三角形的三边关系:任意两边之和>第三边,任意两边之差<第三边;注意情况的多解和取舍.
从4条线段里任取3条线段组合,可有4种情况,看哪种情况不符合三角形三边关系,舍去即可.
四条木棒的所有组合:3,6,8和3,6,9和6,8,9和3,8,9;
只有3,6,8和6,8,9;3,8,9能组成三角形.
故选:C.
拓展3
【答案】B
【解析】根据三角形的三边关系定理来确定腰长x的取值范围.
若是等腰三角形,需满足的条件是:,解得
拓展4
【答案】C
【解析】∵a、b、c是△ABC三边长,
∴a+b+c>0,a+b-c>0,a-b-c<0,
∴M=(a+b+c)(a+b-c)(a-b-c).
拓展5
【答案】C
【解析】
解:∵∠C=100°,
∴AB>AC,
如图,取BC的中点E,则BE=CE,
∴AB+BE>AC+CE,
由三角形三边关系,AC+BC>AB,
∴AB<AD,
∴AD的中点M在BE上,
即点M在BC上,且距点B较近,距点C较远.
故选C.
拓展6
【答案】A
【解析】已知,在△ABC中,∠C=90°,AC=3,
根据垂线段最短,可知AP的长不可小于3,当P和C重合时,AP=3,
拓展7
【答案】见解析
【解析】∵在△中,
在△中,∴
∴
∴
拓展8
【答案】5
拓展9
【答案】B
【解析】工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.
拓展10
【答案】C
拓展11
【答案】7
【解析】
如图,连接AB1,BC1,CA1,
∵A、B分别是线段A1B,B1C的中点,
∴S△
ABB1=S△
ABC=1,
S△
A1AB1=S△
ABB1=1,
∴S△
A1BB1=S△
A1AB1+S△
ABB1=1+1=2,
同理:S△
B1CC1=2,S△
A1AC1=2,
∴△A1B1C1的面积=S△
A1BB1+S△
B1CC1+S△
A1AC1+S△
ABC=2+2+2+1=7.
故答案为:7.
拓展12
【答案】5
【解析】该题考察的是面积计算.
运用求差法:全部的面积减去空白的面积就是红色的面积.设小长方形长为2,宽为.
.
拓展13
【答案】D
【解析】该题考查的是面积问题.
在△ABC中,△AOB与△COB
同高,所以,同理可得,所以,所以,该题答案选D.
拓展14
【答案】见下图
【解析】三角形一边上的中线可以把三角形分成两个面积相等的小三角形,因此本题可以利用中线设计划分方案.
拓展15
【答案】(1),,(2)见解析
【解析】该题考查的是尺规作图.
(1)因为平行线间的距离相等,所以,,;
(2)连接MC;过AB中点D作DE//MC交BC于点E;作直线ME,ME为过点M平分三角形面积的直线.
拓展16
【答案】
【解析】∵点E为AC的中点,
∴S△ABE=S△ABC.
∵BD:CD=2:3,
∴S△ABD=S△ABC,
∵S△AOE-S△BOD=1,
∴S△ABE-S△ABD=S△ABC-S△ABC=1,
解得S△ABC=10.
故答案为:10
0
