沪科版(2012)初中数学八年级下册 17.1 一元二次方程 教案
文档属性
| 名称 | 沪科版(2012)初中数学八年级下册 17.1 一元二次方程 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 53.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 22:13:44 | ||
图片预览

文档简介
17.1一元二次方程
【学习目标】
知识与技能
1、了解一元二次方程的概念。
2、掌握一元二次方程的一般形式,会将一元二次方程化成一般形式,会辨认一元二次方程的二次项系数、一次项系数和常数项.
3、解决一些干概念性的题目。
过程与方法
经历对生活中一元二次方程实例的认识过程,培养观察问题、发现问题、分析问题、解决问题的能力和概括、转化问题的能力。
情感、态度与价值观
通过用数学知识解决生活中实际问题的方式来激发学习的热情、发展数学应用意识、提高学习数学的兴趣。
【学习重、难点】
重点:一元二次方程的概念,包括它的一般形式.
难点:会辨认一元二次方程的二次项系数、一次项系数和常数项.
【导学过程】
(一)预习导学
一.温故知新
1.下列是一元一次方程的有(
)个.
①,
②,
③
,
④
,
⑤
A.1个
B.2个
C.3个
D.4个
2.根据题意,列方程:
(1)边长为a的正方形,面积等于12,求其边长a;
方程为:
.
(2)一个长方形的长比宽多2,面积是48,求这个长方形的长x.
方程为:
.
二.感受新知
1.什么是一元二次方程?请举几个例子(不少于3个).
2.把下列方程化成一般形式(即标准形式),并指出它的二次项系数,一次项系数及常数项:
(1);
(2).
(二)合作交流
一.小组交流
列方程,不求解:
1.某地为增加农民收入,需要调整农作物种植结构,2007年无公害蔬菜的产量比2005年翻一翻.要实现这一目标,2006年和2007年无公害蔬菜产量的年平均增长率应是多少?
分析:
①“翻一翻”在题目中是指
.
②“平均增长率”指
.
解:设无公害蔬菜产量的年平均增长率是,2005年的产量为,则2006年的无公害蔬菜产量为
;那么2007年无公害蔬菜产量为
.
根据2005年与2007年无公害蔬菜产量的关系,可列方程为:
=
.
进一步化简可得
①
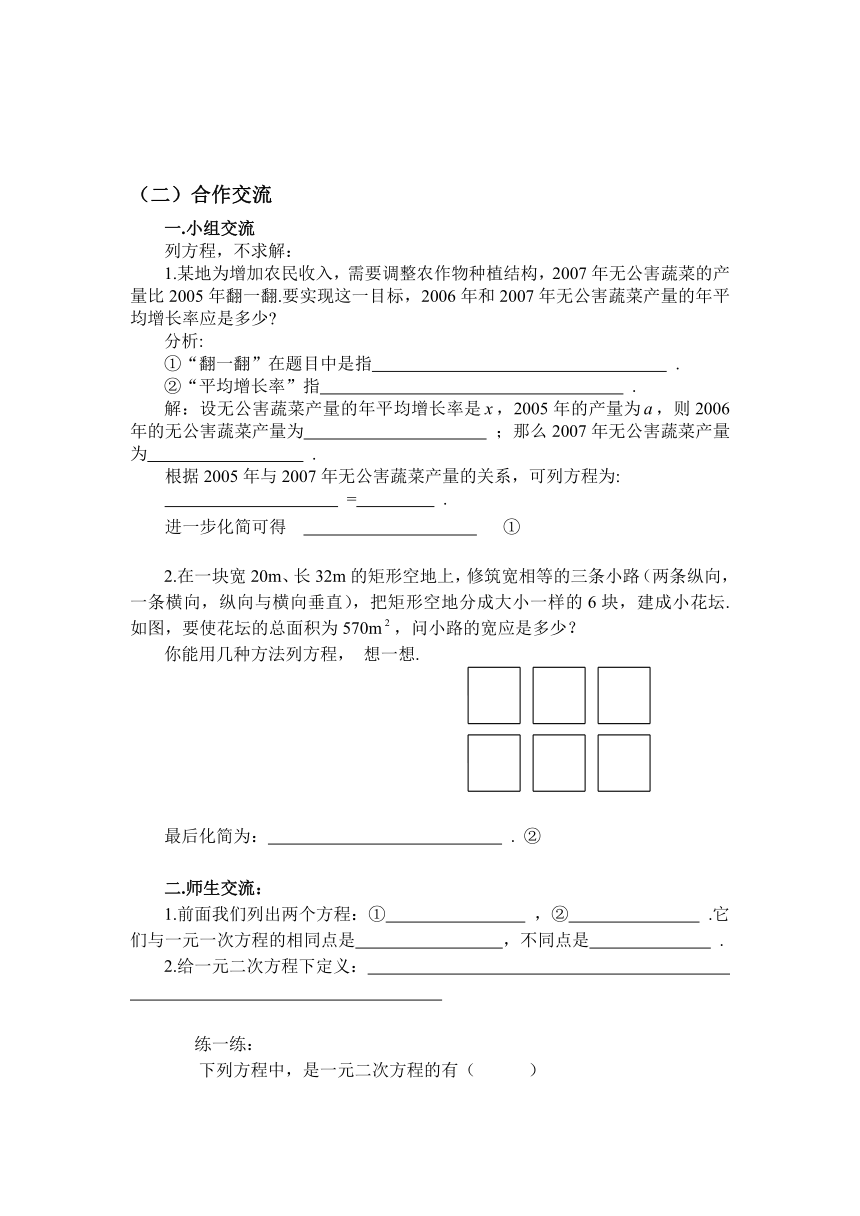
2.在一块宽20m、长32m的矩形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把矩形空地分成大小一样的6块,建成小花坛.如图,要使花坛的总面积为570m,问小路的宽应是多少?
你能用几种方法列方程,
想一想.
最后化简为:
.
②
二.师生交流:
1.前面我们列出两个方程:①
,②
.它们与一元一次方程的相同点是
,不同点是
.
2.给一元二次方程下定义:
练一练:
下列方程中,是一元二次方程的有(
)
(1);
(2);
(3);
(4);
(5);
(6)
3.一元二次方程的一般形式:任何一个二元一次方程,经过整理都可化为形如:把它叫做一元二次方程的
(又叫做
).其中
叫做二次项,
是二次项的系数;
叫做一次项,
是一次项的系数;
叫做常数项.
≠0.
试一试:
把方程化为一般形式,并写出它的二次项系数、一次项系数及常数项.
(三)巩固拓展
1.下列是关于的一元二次方程的为(
)
A.
B.
C.
D.
2.方程的一次项系数是
,当k=
时,关于x的
方程有一个根是0.
3.
把下列一元二次方程化成一般形式,并指出它们的二次项系数、一次项系数及常数项分别是多少?
(1)
;
(2).
4.一元二次方程的一个根是x=1,且a、b满足等式,求此一元二次方程.
5.方程是关于x的一元二次方程吗?请说明理由。
6.若是关于x一元二次方程,小明求得a=1,b=0.你认为他的结论正确吗?为什么?
小结:本节课你有哪些收获?
【课后反思】
【学习目标】
知识与技能
1、了解一元二次方程的概念。
2、掌握一元二次方程的一般形式,会将一元二次方程化成一般形式,会辨认一元二次方程的二次项系数、一次项系数和常数项.
3、解决一些干概念性的题目。
过程与方法
经历对生活中一元二次方程实例的认识过程,培养观察问题、发现问题、分析问题、解决问题的能力和概括、转化问题的能力。
情感、态度与价值观
通过用数学知识解决生活中实际问题的方式来激发学习的热情、发展数学应用意识、提高学习数学的兴趣。
【学习重、难点】
重点:一元二次方程的概念,包括它的一般形式.
难点:会辨认一元二次方程的二次项系数、一次项系数和常数项.
【导学过程】
(一)预习导学
一.温故知新
1.下列是一元一次方程的有(
)个.
①,
②,
③
,
④
,
⑤
A.1个
B.2个
C.3个
D.4个
2.根据题意,列方程:
(1)边长为a的正方形,面积等于12,求其边长a;
方程为:
.
(2)一个长方形的长比宽多2,面积是48,求这个长方形的长x.
方程为:
.
二.感受新知
1.什么是一元二次方程?请举几个例子(不少于3个).
2.把下列方程化成一般形式(即标准形式),并指出它的二次项系数,一次项系数及常数项:
(1);
(2).
(二)合作交流
一.小组交流
列方程,不求解:
1.某地为增加农民收入,需要调整农作物种植结构,2007年无公害蔬菜的产量比2005年翻一翻.要实现这一目标,2006年和2007年无公害蔬菜产量的年平均增长率应是多少?
分析:
①“翻一翻”在题目中是指
.
②“平均增长率”指
.
解:设无公害蔬菜产量的年平均增长率是,2005年的产量为,则2006年的无公害蔬菜产量为
;那么2007年无公害蔬菜产量为
.
根据2005年与2007年无公害蔬菜产量的关系,可列方程为:
=
.
进一步化简可得
①
2.在一块宽20m、长32m的矩形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把矩形空地分成大小一样的6块,建成小花坛.如图,要使花坛的总面积为570m,问小路的宽应是多少?
你能用几种方法列方程,
想一想.
最后化简为:
.
②
二.师生交流:
1.前面我们列出两个方程:①
,②
.它们与一元一次方程的相同点是
,不同点是
.
2.给一元二次方程下定义:
练一练:
下列方程中,是一元二次方程的有(
)
(1);
(2);
(3);
(4);
(5);
(6)
3.一元二次方程的一般形式:任何一个二元一次方程,经过整理都可化为形如:把它叫做一元二次方程的
(又叫做
).其中
叫做二次项,
是二次项的系数;
叫做一次项,
是一次项的系数;
叫做常数项.
≠0.
试一试:
把方程化为一般形式,并写出它的二次项系数、一次项系数及常数项.
(三)巩固拓展
1.下列是关于的一元二次方程的为(
)
A.
B.
C.
D.
2.方程的一次项系数是
,当k=
时,关于x的
方程有一个根是0.
3.
把下列一元二次方程化成一般形式,并指出它们的二次项系数、一次项系数及常数项分别是多少?
(1)
;
(2).
4.一元二次方程的一个根是x=1,且a、b满足等式,求此一元二次方程.
5.方程是关于x的一元二次方程吗?请说明理由。
6.若是关于x一元二次方程,小明求得a=1,b=0.你认为他的结论正确吗?为什么?
小结:本节课你有哪些收获?
【课后反思】
