第3章代数式 单元检测-苏科版七年级数学上册(Word版 含解析)
文档属性
| 名称 | 第3章代数式 单元检测-苏科版七年级数学上册(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 39.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 15:23:47 | ||
图片预览

文档简介
第3章《代数式》单元检测
(时间:60分钟
满分100分)
一、选择题(每小题3分,共24分)
1.下列式子中,是单项式的是( )
A.x3yz2
B.x﹣y
C.m2﹣n2
D.
2.下列各组单项式中是同类项的是( )
A.2a2b与﹣3ab2
B.﹣m2n3与3m2n3
C.4xy与4x2y2
D.﹣a2b与a2c
3.已知x=2,则代数式﹣x2+5的值为( )
A.9
B.1
C.7
D.3
4.多项式2x2﹣5x2y﹣y2﹣3的次数和三次项分别是( )
A.2和5x2y
B.3和5x2y
C.4和﹣5x2y
D.3和﹣5x2y
5.已知2y2+y﹣2的值为3,则4y2+2y+1的值为( )
A.10
B.11
C.10或11
D.3或11
6.下列运算结果正确的是( )
A.2a+2b=4ab
B.9ab﹣a=8ab
C.4x5+6x2=10x7
D.9a2b﹣9ba2=0
7.对于单项式15a,解释不合理的是( )
A.排骨的市场价是15
元/千克,买a千克需15a元
B.排骨的市场价是a元/千克,买15千克需15a元
C.某车行驶速度为akm/h,行驶了15h共耗油15aL
D.某电梯里有15个人,平均每人重a千克,则这15人共重15a千克
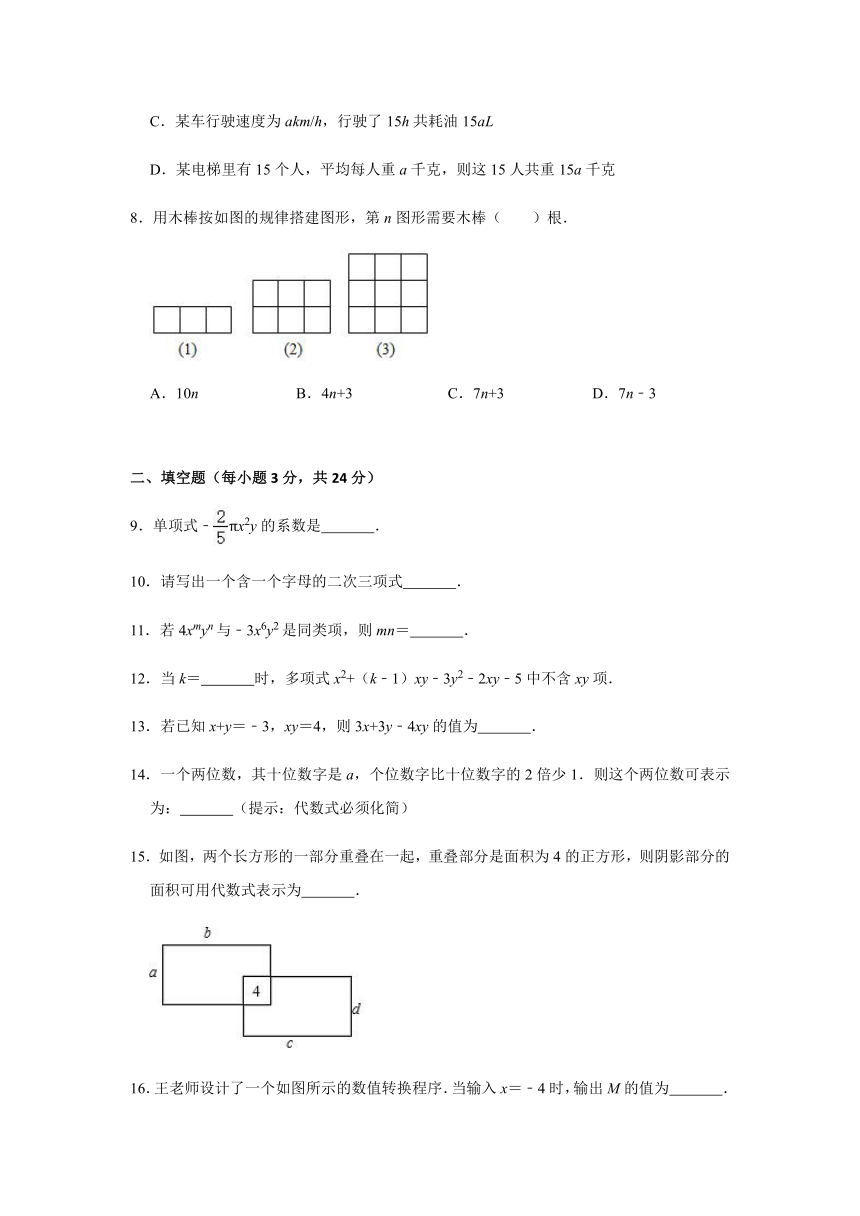
8.用木棒按如图的规律搭建图形,第n图形需要木棒( )根.
A.10n
B.4n+3
C.7n+3
D.7n﹣3
二、填空题(每小题3分,共24分)
9.单项式﹣πx2y的系数是
.
10.请写出一个含一个字母的二次三项式
.
11.若4xmyn与﹣3x6y2是同类项,则mn=
.
12.当k=
时,多项式x2+(k﹣1)xy﹣3y2﹣2xy﹣5中不含xy项.
13.若已知x+y=﹣3,xy=4,则3x+3y﹣4xy的值为
.
14.一个两位数,其十位数字是a,个位数字比十位数字的2倍少1.则这个两位数可表示为:
(提示:代数式必须化简)
15.如图,两个长方形的一部分重叠在一起,重叠部分是面积为4的正方形,则阴影部分的面积可用代数式表示为
.
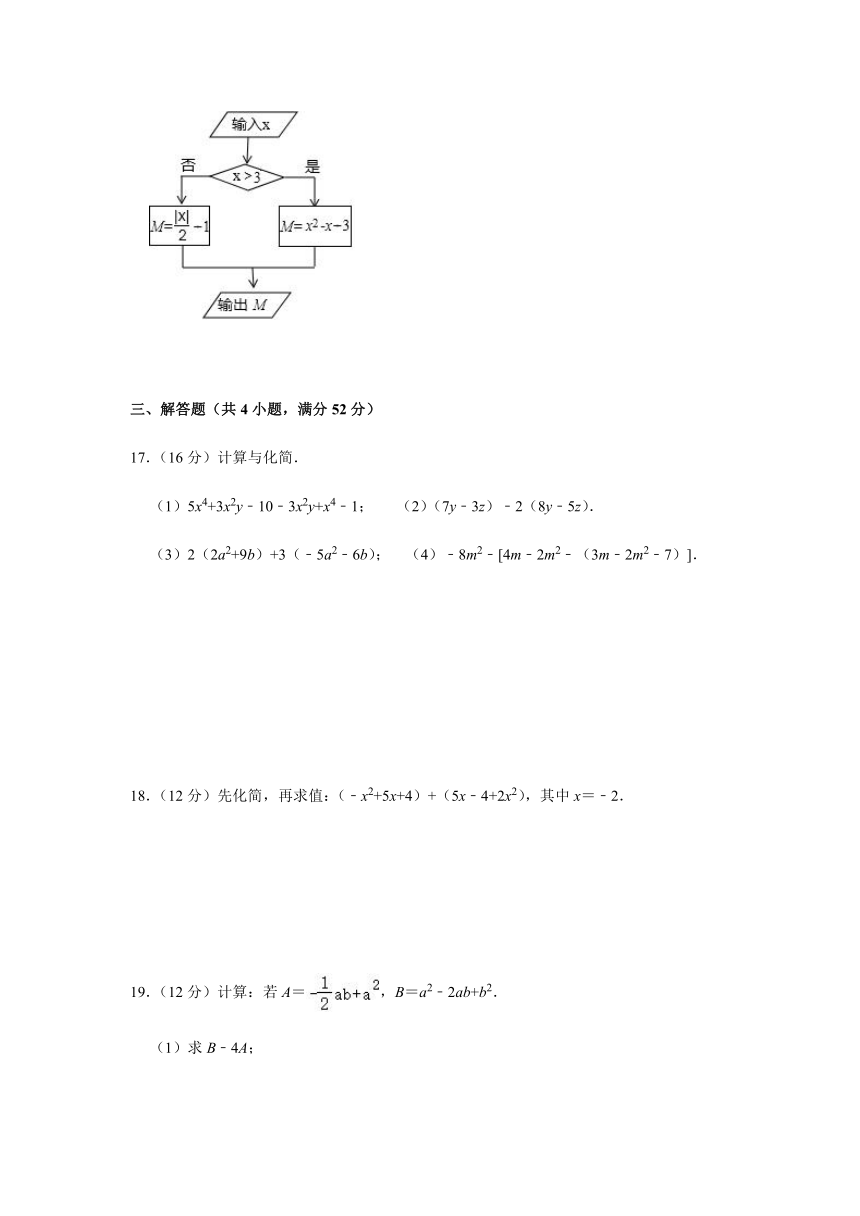
16.王老师设计了一个如图所示的数值转换程序.当输入x=﹣4时,输出M的值为
.
三、解答题(共4小题,满分52分)
17.(16分)计算与化简.
(1)5x4+3x2y﹣10﹣3x2y+x4﹣1;
(2)(7y﹣3z)﹣2(8y﹣5z).
(3)2(2a2+9b)+3(﹣5a2﹣6b);
(4)﹣8m2﹣[4m﹣2m2﹣(3m﹣2m2﹣7)].
18.(12分)先化简,再求值:(﹣x2+5x+4)+(5x﹣4+2x2),其中x=﹣2.
19.(12分)计算:若A=,B=a2﹣2ab+b2.
(1)求B﹣4A;
(2)当a=,b=﹣2时,求B﹣4A的值.
20.(12分)已知(x+1)2+|y﹣2|=0,先化简,再求代数式:4(x2﹣3xy﹣y2)﹣3(x2﹣7xy﹣2y2)的值.
第2章单元检测参考答案
1.A
解析:A、﹣x3yz2,是单项式;B、x﹣y不是单项式;
C、m2﹣n2不是单项式;D、不是单项式;故选:A.
2.B
解析:A、2a2b与﹣3ab2,相同字母的指数不相同,不是同类项;
B、﹣m2n3与3m2n3
,所含字母相同,相同字母的指数相同,是同类项;
C、4xy与4x2y2,相同字母的指数不相同,不是同类项;
D、﹣a2b与a2c,所含字母不相同,不是同类项;故选:B.
3.B
解析:∵x=2,∴﹣x2+5=﹣22+5=﹣4+5=1.故选:B.
4.D
解析:多项式2x2﹣5x2y﹣y2﹣3的次数和三次项分别为3,﹣5x2y,故选:D.
5.B
解析:∵2y2+y﹣2的值为3,∴2y2+y﹣2=3,∴2y2+y=5,
∴2(2y2+y)=4y2+2y=10,∴4y2+2y+1=11.故选:B.
6.D
解析:A.2a与2b不是同类项,不能合并,此选项错误;
B.9ab与a不是同类项,不能合并,此选项错误;
C.4x5与6x2不是同类项,不能合并,此选项错误;
D.9a2b﹣9ba2=0,此选项正确;故选:D.
7.C
解析:A、B、D都解释合理,不符合题意;
C、某车行驶速度为akm/h,行驶了15h共行驶15akm,故选项解释不合理,符合题意.
故选:C.
8.C
解析:观察图形知:
第①个图形有3+7=10根木棒;第②个图形有3+7×2=17根木棒;
第③个图形有3+7×3=24根木棒;…第n个图形有7n+3根木棒,故选:C.
9.解析:﹣πx2y的系数是﹣π,故答案为:﹣π.
10.解析:二次三项式为x2﹣2x+3,故答案为:x2﹣2x+3(答案不唯一).
11.解析:∵4xmyn与﹣3x6y2是同类项,∴m=6,n=2,∴mn=6×2=12,
故答案为:12.
12.解析:整理只含xy的项得:(k﹣3)xy,∴k﹣3=0,k=3.故答案为:3.
13.解析:∵x+y=﹣3,xy=4,∴3x+3y﹣4xy=3(x+y)﹣4xy=3×(﹣3)﹣4×4=﹣9﹣16=﹣25,
故答案为:﹣25.
14.解析:由题意可得:10a+2a﹣1=12a﹣1.故答案为:12a﹣1.
15.解析:由图可得,阴影部分的面积是:ab+cd﹣4×2=ab+cd﹣8,
故答案为:ab+cd﹣8.
16.解析:当x=﹣4时,M=+1=+1=2+1=3,
故答案为:3.
17.解:(1)5x4+3x2y﹣10﹣3x2y+x4﹣1=6x4﹣11;
(2)(7y﹣3z)﹣2(8y﹣5z)=7y﹣3z﹣16y+10z=﹣9y+7z;
(3)2(2a2+9b)+3(﹣5a2﹣6b)=4a2+18b﹣15a2﹣18b=﹣11a2;
(4)﹣8m2﹣[4m﹣2m2﹣(3m﹣2m2﹣7)]
=﹣8m2﹣4m+2m2+(3m﹣2m2﹣7)=﹣8m2﹣4m+2m2+3m﹣2m2﹣7=﹣8m2﹣m﹣7.
18.解:原式=(﹣x2+5x+4)+(5x﹣4+2x2)=﹣x2+5x+4+5x﹣4+2x2=x2+10x
=x(x+10).
∵x=﹣2,∴原式=﹣16.
19.解:(1)B﹣4A=(a2﹣2ab+b2)﹣4()
=a2﹣2ab+b2+2ab﹣4a2=﹣3a2+b2;
(2)当a=,b=﹣2,原式=﹣3a2+b2=+(﹣2)2
=+4=.
20.解:原式=2x2﹣12xy﹣4y2﹣3x2+21xy+6y2=﹣x2+9xy+2y2,
∵(x+1)2+|y﹣2|=0,∴x+1=0,y﹣2=0,∴x=﹣1,y=2,
原式=﹣1+9×(﹣1)×2+2×4=﹣1﹣18+8=﹣11.
(时间:60分钟
满分100分)
一、选择题(每小题3分,共24分)
1.下列式子中,是单项式的是( )
A.x3yz2
B.x﹣y
C.m2﹣n2
D.
2.下列各组单项式中是同类项的是( )
A.2a2b与﹣3ab2
B.﹣m2n3与3m2n3
C.4xy与4x2y2
D.﹣a2b与a2c
3.已知x=2,则代数式﹣x2+5的值为( )
A.9
B.1
C.7
D.3
4.多项式2x2﹣5x2y﹣y2﹣3的次数和三次项分别是( )
A.2和5x2y
B.3和5x2y
C.4和﹣5x2y
D.3和﹣5x2y
5.已知2y2+y﹣2的值为3,则4y2+2y+1的值为( )
A.10
B.11
C.10或11
D.3或11
6.下列运算结果正确的是( )
A.2a+2b=4ab
B.9ab﹣a=8ab
C.4x5+6x2=10x7
D.9a2b﹣9ba2=0
7.对于单项式15a,解释不合理的是( )
A.排骨的市场价是15
元/千克,买a千克需15a元
B.排骨的市场价是a元/千克,买15千克需15a元
C.某车行驶速度为akm/h,行驶了15h共耗油15aL
D.某电梯里有15个人,平均每人重a千克,则这15人共重15a千克
8.用木棒按如图的规律搭建图形,第n图形需要木棒( )根.
A.10n
B.4n+3
C.7n+3
D.7n﹣3
二、填空题(每小题3分,共24分)
9.单项式﹣πx2y的系数是
.
10.请写出一个含一个字母的二次三项式
.
11.若4xmyn与﹣3x6y2是同类项,则mn=
.
12.当k=
时,多项式x2+(k﹣1)xy﹣3y2﹣2xy﹣5中不含xy项.
13.若已知x+y=﹣3,xy=4,则3x+3y﹣4xy的值为
.
14.一个两位数,其十位数字是a,个位数字比十位数字的2倍少1.则这个两位数可表示为:
(提示:代数式必须化简)
15.如图,两个长方形的一部分重叠在一起,重叠部分是面积为4的正方形,则阴影部分的面积可用代数式表示为
.
16.王老师设计了一个如图所示的数值转换程序.当输入x=﹣4时,输出M的值为
.
三、解答题(共4小题,满分52分)
17.(16分)计算与化简.
(1)5x4+3x2y﹣10﹣3x2y+x4﹣1;
(2)(7y﹣3z)﹣2(8y﹣5z).
(3)2(2a2+9b)+3(﹣5a2﹣6b);
(4)﹣8m2﹣[4m﹣2m2﹣(3m﹣2m2﹣7)].
18.(12分)先化简,再求值:(﹣x2+5x+4)+(5x﹣4+2x2),其中x=﹣2.
19.(12分)计算:若A=,B=a2﹣2ab+b2.
(1)求B﹣4A;
(2)当a=,b=﹣2时,求B﹣4A的值.
20.(12分)已知(x+1)2+|y﹣2|=0,先化简,再求代数式:4(x2﹣3xy﹣y2)﹣3(x2﹣7xy﹣2y2)的值.
第2章单元检测参考答案
1.A
解析:A、﹣x3yz2,是单项式;B、x﹣y不是单项式;
C、m2﹣n2不是单项式;D、不是单项式;故选:A.
2.B
解析:A、2a2b与﹣3ab2,相同字母的指数不相同,不是同类项;
B、﹣m2n3与3m2n3
,所含字母相同,相同字母的指数相同,是同类项;
C、4xy与4x2y2,相同字母的指数不相同,不是同类项;
D、﹣a2b与a2c,所含字母不相同,不是同类项;故选:B.
3.B
解析:∵x=2,∴﹣x2+5=﹣22+5=﹣4+5=1.故选:B.
4.D
解析:多项式2x2﹣5x2y﹣y2﹣3的次数和三次项分别为3,﹣5x2y,故选:D.
5.B
解析:∵2y2+y﹣2的值为3,∴2y2+y﹣2=3,∴2y2+y=5,
∴2(2y2+y)=4y2+2y=10,∴4y2+2y+1=11.故选:B.
6.D
解析:A.2a与2b不是同类项,不能合并,此选项错误;
B.9ab与a不是同类项,不能合并,此选项错误;
C.4x5与6x2不是同类项,不能合并,此选项错误;
D.9a2b﹣9ba2=0,此选项正确;故选:D.
7.C
解析:A、B、D都解释合理,不符合题意;
C、某车行驶速度为akm/h,行驶了15h共行驶15akm,故选项解释不合理,符合题意.
故选:C.
8.C
解析:观察图形知:
第①个图形有3+7=10根木棒;第②个图形有3+7×2=17根木棒;
第③个图形有3+7×3=24根木棒;…第n个图形有7n+3根木棒,故选:C.
9.解析:﹣πx2y的系数是﹣π,故答案为:﹣π.
10.解析:二次三项式为x2﹣2x+3,故答案为:x2﹣2x+3(答案不唯一).
11.解析:∵4xmyn与﹣3x6y2是同类项,∴m=6,n=2,∴mn=6×2=12,
故答案为:12.
12.解析:整理只含xy的项得:(k﹣3)xy,∴k﹣3=0,k=3.故答案为:3.
13.解析:∵x+y=﹣3,xy=4,∴3x+3y﹣4xy=3(x+y)﹣4xy=3×(﹣3)﹣4×4=﹣9﹣16=﹣25,
故答案为:﹣25.
14.解析:由题意可得:10a+2a﹣1=12a﹣1.故答案为:12a﹣1.
15.解析:由图可得,阴影部分的面积是:ab+cd﹣4×2=ab+cd﹣8,
故答案为:ab+cd﹣8.
16.解析:当x=﹣4时,M=+1=+1=2+1=3,
故答案为:3.
17.解:(1)5x4+3x2y﹣10﹣3x2y+x4﹣1=6x4﹣11;
(2)(7y﹣3z)﹣2(8y﹣5z)=7y﹣3z﹣16y+10z=﹣9y+7z;
(3)2(2a2+9b)+3(﹣5a2﹣6b)=4a2+18b﹣15a2﹣18b=﹣11a2;
(4)﹣8m2﹣[4m﹣2m2﹣(3m﹣2m2﹣7)]
=﹣8m2﹣4m+2m2+(3m﹣2m2﹣7)=﹣8m2﹣4m+2m2+3m﹣2m2﹣7=﹣8m2﹣m﹣7.
18.解:原式=(﹣x2+5x+4)+(5x﹣4+2x2)=﹣x2+5x+4+5x﹣4+2x2=x2+10x
=x(x+10).
∵x=﹣2,∴原式=﹣16.
19.解:(1)B﹣4A=(a2﹣2ab+b2)﹣4()
=a2﹣2ab+b2+2ab﹣4a2=﹣3a2+b2;
(2)当a=,b=﹣2,原式=﹣3a2+b2=+(﹣2)2
=+4=.
20.解:原式=2x2﹣12xy﹣4y2﹣3x2+21xy+6y2=﹣x2+9xy+2y2,
∵(x+1)2+|y﹣2|=0,∴x+1=0,y﹣2=0,∴x=﹣1,y=2,
原式=﹣1+9×(﹣1)×2+2×4=﹣1﹣18+8=﹣11.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
