华东师大版八年级数学下册导学案:16.2.2 分式的加减
文档属性
| 名称 | 华东师大版八年级数学下册导学案:16.2.2 分式的加减 |
|
|
| 格式 | zip | ||
| 文件大小 | 747.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 22:43:47 | ||
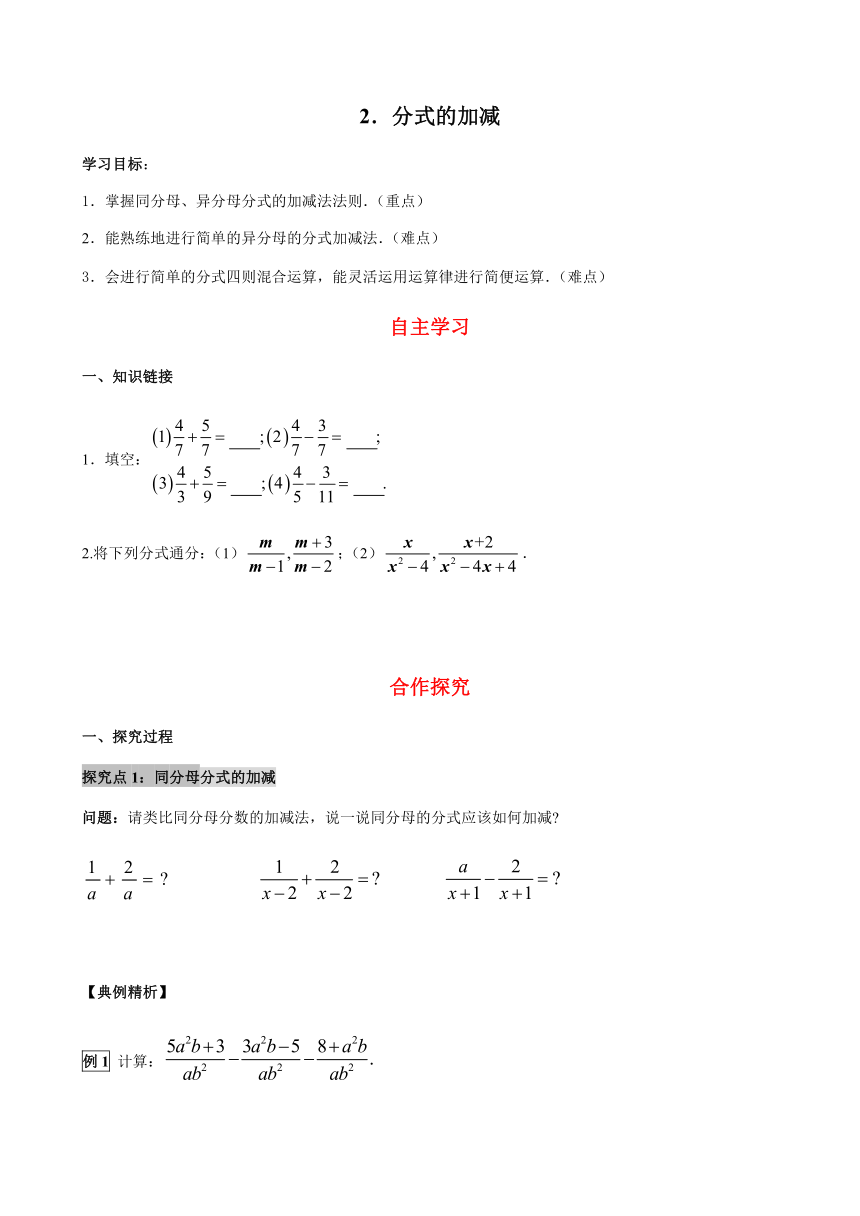
图片预览



文档简介
2.分式的加减
学习目标:
1.掌握同分母、异分母分式的加减法法则.(重点)
2.能熟练地进行简单的异分母的分式加减法.(难点)
3.会进行简单的分式四则混合运算,能灵活运用运算律进行简便运算.(难点)
自主学习
一、知识链接
1.填空:
将下列分式通分:(1);(2).
合作探究
一、探究过程
探究点1:同分母分式的加减
问题:请类比同分母分数的加减法,说一说同分母的分式应该如何加减?
【典例精析】
例1
计算:
【方法总结】(1)当分子是多项式,把分子相减时,千万不要忘记加括号;(2)分式加减运算的结果,必须要化成最简分式或整式.
探究点2:异分母分式的加减
问题:请类比异分母分数的加减法,说一说异分母的分式应该如何加减?
【典例精析】
例2计算:(1);(2).
【方法总结】异分母分式相加减:(1)当两个分式的分母互为相反数时,可直接变形为同分母的分式,再相加减;(2)分母是多项式时,先因式分解找出最简公分母,再通分,转化为同分母的分式相加减.
【针对训练】1.计算的结果是(
)
A.
B.
C.
D.
【典例精析】
例3计算:.
【方法总结】分式与整式相加减,把整式看成分母为“1”的分式,然后通分,转化为同分母的分式相加减.
【针对训练】2.计算a-b+的结果为(
)
A.
B.a+b
C.
D.以上都不对
探究点3:分式的混合运算
问题:如何计算
?请先思考这道题包含的运算,确定运算顺序,再独立完成.
【要点归纳】分式混合运算的顺序:先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.计算结果要化为最简分式或整式.
【典例精析】
例4
计算:(1);
(2).
【针对训练】3.先化简代数式÷(1-),再从-4<x<4的范围内选取一个合适的整数x代入求值.
【方法总结】把分式化成最简分式是解题的关键,通分、因式分解和约分是基本环节,注意选数时,分母不能为0.
二、课堂小结
内容
同分母分式的加减
分母________,把________相加减.即±=_______.
异分母分式的加减
先________,变为同分母的分式,再________.即±=____±____=________.
分式的混合运算
先________,再________,然后________,有括号的先算括号里面的.最后结果中分子、分母要进行约分,注意运算的结果要化成____________或整式.
解题策略
一个分式与一个整式相加减时,可以把整式看做是分母为“1”的式子,整式前面是负号时,要加括号,进行通分.
分母是多项式时,先因式分解找出最简公分母,再通分,转化为同分母的分式相加减.
(3)结果一定要化成最简分式或整式.
当堂检测
1.计算
的结果为(
)
A.
B.
C.
-1
D.2
2.填空:;.
3.计算:
(1)
;
(2)
;
(3)
;
(4)
.
4.计算:
(1)
;
(2)
.
5.先化简:.当b=3时,从-2合适的整数a代入求值.
参考答案
自主学习
一、知识链接
1.(1)
(2)
(3)
(4)
2.解:(1)最简公分母:(m-1)(m-2),,;(2)最简公分母:(x+2)(x-2)2,,.
合作探究
一、探究过程
探究点1:同分母分式的加减
解:;;.
同分母的分式的加减,分母不变,分子相加减.
【典例精析】
例1
解:原式=
探究点2:异分母分式的加减
解:;.
异分母的分式的加减,先通分,变为同分母的分式,然后再加减.
【典例精析】
例2
解:(1)原式=.
(2)原式=.
【针对训练】1.B
例3
解:原式=.
【针对训练】2.C
探究点3:分式的混合运算
解:原式包括乘方、乘法、除法、减法运算,应先算乘方,再算乘除法,然后算减法.
原式==.
【典例精析】
例4
解:(1)原式=.
(2)原式=.
【针对训练】3.解:原式=.∵-4<x<4,x≠±1,x≠2,∴x可取的整数值为±3,-2,0.若取x=3,原式=2.
二、课堂小结
不变
分子
通分
加减
乘方
乘除
加减
最简分式
当堂检测
1.C
2.(1)
(2)4
3.解:(1)原式=.
(2)原式=.
(3)原式=.
(4)原式=.
4.解:(1)原式==x.
(2)原式=.
5.解:原式=.
当b=3时,∵-2<a<2,a≠0且a≠±3,∴a的整数值为±1.若取a=1,则原式=.
学习目标:
1.掌握同分母、异分母分式的加减法法则.(重点)
2.能熟练地进行简单的异分母的分式加减法.(难点)
3.会进行简单的分式四则混合运算,能灵活运用运算律进行简便运算.(难点)
自主学习
一、知识链接
1.填空:
将下列分式通分:(1);(2).
合作探究
一、探究过程
探究点1:同分母分式的加减
问题:请类比同分母分数的加减法,说一说同分母的分式应该如何加减?
【典例精析】
例1
计算:
【方法总结】(1)当分子是多项式,把分子相减时,千万不要忘记加括号;(2)分式加减运算的结果,必须要化成最简分式或整式.
探究点2:异分母分式的加减
问题:请类比异分母分数的加减法,说一说异分母的分式应该如何加减?
【典例精析】
例2计算:(1);(2).
【方法总结】异分母分式相加减:(1)当两个分式的分母互为相反数时,可直接变形为同分母的分式,再相加减;(2)分母是多项式时,先因式分解找出最简公分母,再通分,转化为同分母的分式相加减.
【针对训练】1.计算的结果是(
)
A.
B.
C.
D.
【典例精析】
例3计算:.
【方法总结】分式与整式相加减,把整式看成分母为“1”的分式,然后通分,转化为同分母的分式相加减.
【针对训练】2.计算a-b+的结果为(
)
A.
B.a+b
C.
D.以上都不对
探究点3:分式的混合运算
问题:如何计算
?请先思考这道题包含的运算,确定运算顺序,再独立完成.
【要点归纳】分式混合运算的顺序:先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.计算结果要化为最简分式或整式.
【典例精析】
例4
计算:(1);
(2).
【针对训练】3.先化简代数式÷(1-),再从-4<x<4的范围内选取一个合适的整数x代入求值.
【方法总结】把分式化成最简分式是解题的关键,通分、因式分解和约分是基本环节,注意选数时,分母不能为0.
二、课堂小结
内容
同分母分式的加减
分母________,把________相加减.即±=_______.
异分母分式的加减
先________,变为同分母的分式,再________.即±=____±____=________.
分式的混合运算
先________,再________,然后________,有括号的先算括号里面的.最后结果中分子、分母要进行约分,注意运算的结果要化成____________或整式.
解题策略
一个分式与一个整式相加减时,可以把整式看做是分母为“1”的式子,整式前面是负号时,要加括号,进行通分.
分母是多项式时,先因式分解找出最简公分母,再通分,转化为同分母的分式相加减.
(3)结果一定要化成最简分式或整式.
当堂检测
1.计算
的结果为(
)
A.
B.
C.
-1
D.2
2.填空:;.
3.计算:
(1)
;
(2)
;
(3)
;
(4)
.
4.计算:
(1)
;
(2)
.
5.先化简:.当b=3时,从-2
参考答案
自主学习
一、知识链接
1.(1)
(2)
(3)
(4)
2.解:(1)最简公分母:(m-1)(m-2),,;(2)最简公分母:(x+2)(x-2)2,,.
合作探究
一、探究过程
探究点1:同分母分式的加减
解:;;.
同分母的分式的加减,分母不变,分子相加减.
【典例精析】
例1
解:原式=
探究点2:异分母分式的加减
解:;.
异分母的分式的加减,先通分,变为同分母的分式,然后再加减.
【典例精析】
例2
解:(1)原式=.
(2)原式=.
【针对训练】1.B
例3
解:原式=.
【针对训练】2.C
探究点3:分式的混合运算
解:原式包括乘方、乘法、除法、减法运算,应先算乘方,再算乘除法,然后算减法.
原式==.
【典例精析】
例4
解:(1)原式=.
(2)原式=.
【针对训练】3.解:原式=.∵-4<x<4,x≠±1,x≠2,∴x可取的整数值为±3,-2,0.若取x=3,原式=2.
二、课堂小结
不变
分子
通分
加减
乘方
乘除
加减
最简分式
当堂检测
1.C
2.(1)
(2)4
3.解:(1)原式=.
(2)原式=.
(3)原式=.
(4)原式=.
4.解:(1)原式==x.
(2)原式=.
5.解:原式=.
当b=3时,∵-2<a<2,a≠0且a≠±3,∴a的整数值为±1.若取a=1,则原式=.
