华东师大版九年级数学下册导学案:26.2.1 二次函数y=ax2的图象与性质
文档属性
| 名称 | 华东师大版九年级数学下册导学案:26.2.1 二次函数y=ax2的图象与性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 797.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 00:00:00 | ||
图片预览



文档简介
26.2
二次函数的图象与性质
1.
二次函数y=ax2的图象与性质
学习目标:
1.会用描点法画出二次函数y=ax2
的图象.(重点)
2.根据对特殊函数图象的观察,归纳得出二次函数y=ax2的性质.(难点)
3.进一步理解二次函数和抛物线的有关知识,并能解决一些简单的应用问题.
自主学习
知识链接
一次函数的图象是___________________,反比例函数的图象是_______________.
用描点法画函数图象的步骤:_______________、___________、__________.
下面是一次函数y=x-2的图象,根据图象,你能看出函数的哪些性质?
合作探究
要点探究
探究点1:二次函数y=ax2的图象
画一画
在同一直角坐标系中,画出函数y=2x2与y=-2x2的图象,并指出它们有何共同点?有何不同点?
列表如下:
x
…
-2
-1.5
-1
0
1
1.5
2
…
y=2x2
…
…
y=-2x2
…
…
(2)在如图所示的坐标系中,描点,连线:
(3)观察函数y=2x2与y=-2x2的图象,
写出它们的共同点(至少填写三条):
①:____________________________________________;
②:____________________________________________;
③:____________________________________________.
写出它们的不同点(至少填写三条):
①:____________________________________________;
②:____________________________________________;
③:____________________________________________.
【要点归纳】函数y=ax2的图象是一条抛物线,它是轴对称图形,对称轴是y轴(或直线x=0),抛物线与坐标轴的交点,叫做抛物线的顶点.其顶点坐标为(0,0).
【典例精析】
例1
在同一直角坐标系中,画出函数,的图象.
【针对训练】
在同一直角坐标系中,画出函数,的图象.
【要点归纳】对于抛物线
y
=
ax2,当a>0时,抛物线开口向上,对称轴是y轴,顶点是原点,顶点是抛物线的最低点;当a<0时,抛物线开口向下,对称轴是y轴,顶点是原点,顶点是抛物线的最高点;且|a|越大,抛物线的开口越小.
练一练
1.函数的图象的开口
,对称轴是
,顶点是
;
2.函数的图象的开口
,对称轴是
,顶点是
,顶点是抛物线的最
点;
探究点2:二次函数y=ax2的性质
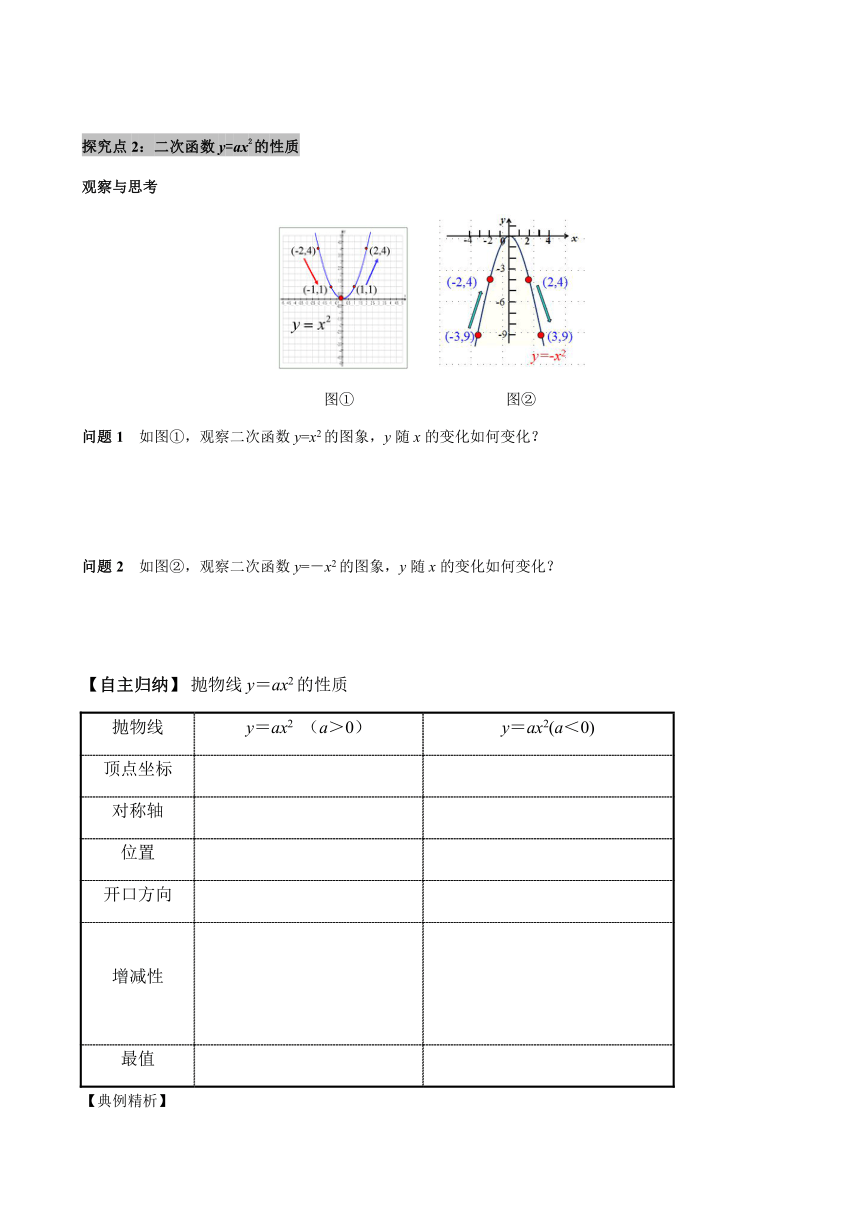
观察与思考
图①
图②
问题1
如图①,观察二次函数y=x2的图象,y随x的变化如何变化?
问题2
如图②,观察二次函数y=-x2的图象,y随x的变化如何变化?
【自主归纳】?抛物线y=ax2的性质
抛物线
y=ax2
(a>0)
y=ax2(a<0)
顶点坐标
对称轴
位置
开口方向
增减性
最值
【典例精析】
例2
已知正方形周长为x
cm,面积为S
cm2.
(1)求S和x之间的函数关系式,并画出图象;
(2)判断点(4,2),(8,4),(-4,1)是否在该函数的图象上.
例3已知是二次函数,且其图象开口向上,求m的值和函数表达式.
【针对训练】已知是二次函数,且当x>0时,y随x增大而增大,则k=
.
例4
已知二次函数y=ax2.
若a=2,点(-2,y1)与(3,y2)在此二次函数的图象上,则y1_____
y2(填“>
”“=”或“<
”);
(2)若a>0,点(2,y1)与(3,y2)在此二次函数的图象上,则
y1_____
y2(填“>
”“=”或“<
”);
(3)若a<0,点(-2,y1)与(3,y2),(5,y3)在此二次函数的图象上,则y1,y2,y3的大小关系是___________.
方法总结:二次函数y=ax2中比较函数值的大小的方法:
①
直接代入法:将x的值分别代入函数表达式中,求出y值再比较大小,多用于a值确定的情况,如例4(1);
②性质判断法:结合二次函数的性质(增减性)及自变量x之间的大小关系,得出其对应y值的大小关系;多用于自变量x在对称轴同一侧的情况,如例4(2);
③草图法:画出二次函数的草图,描点,根据图象直接判断y值的大小.多用于a值不确定且x值不在对称轴同侧的情况,如例4(3).
二、课堂小结
二次函数y=ax2的图象及性质
画法
描点法→在对称轴两侧对称取点
图象
抛物线→轴对称图形
性质
1.开口方向及大小;
2.对称轴;
3.顶点坐标
4.增减性
当堂检测
1.抛物线y=5x2的顶点坐标是
,对称轴是
,在对称轴的
侧,y随着x的增大而增大;在对称轴的
侧,y
随着x的增大而减小,当x
=
时,函数y的值最小,最小值是
.
2.抛物线位置在x轴的
方(除顶点外),在对称轴的左侧,y随着x的增大而
;在对称轴的右侧,y随着x的增大而
,当x=0时,函数y的值最大,最大值是
,当x
0时,y<0.
3.如图,观察函数y=(k-1)x2的图象,则k的取值范围是
.
4.已知抛物线y=ax2的图象经过点A(2,-8),求:
(1)该抛物线的表达式;
(2)判断点B(3,-18)是否在该抛物线上;
(3)求出此抛物线上纵坐标是-50的点的坐标.
5.已知一个二次函数图象上部分点的横坐标x与纵坐标y的对应值如下表所示:
x
…
-4
-2
0
2
4
…
y
…
4
1
0
1
4
…
在给定的坐标系中,画出该二次函数的图象;
(2)求这个二次函数的表达式;
(3)若A(x1,y1),B(x2,y2)在这条抛物线上,且x1y2.
参考答案
自主学习
知识链接
直线
双曲线
列表
描点
连线
解:①一次函数y=x-2的图象经过第一、三、四象限;②函数值y随x的增大而增大
合作探究
一、要点探究
探究点1:二次函数y=ax2的图象
画一画
(1)列表如下:
x
…
-2
-1.5
-1
0
1
1.5
2
…
y=2x2
…
8
4.5
2
0
2
4.5
8
…
y=-2x2
…
-8
-4.5
-2
0
-2
-4.5
-8
…
描点、连线如图①所示.
图①
图②
图③
相同点:①对称轴均为y轴
②顶点坐标均为(0,0)
③开口大小相同
不同点:①开口方向不同;
②y=2x2的图象有最低点,y=-2x2的图象有最高点;③当x<0时,y=2x2的图象呈下降趋势,y=-2x2的图象呈上升趋势
【典例精析】
例1
解:(1)列表如下:
x
…
-3
-1
0
1
3
…
y=x2
…
3
0
3
…
x
…
-2
-1
0
1
2
…
y=x2
…
4
1
0
1
4
…
描点、连线,如图②所示.
【针对训练】
解:(1)列表如下:
x
…
-3
-1
0
1
3
…
y=x2
…
-3
0
-3
…
x
…
-2
-1
0
1
2
…
y=-x2
…
-4
-1
0
-1
-4
…
描点、连线,如图③所示:
练一练
1.向上
y轴
(0,0)
2.向下
y轴
(0,0)
高
3.向上
y轴
(0,0)
低
4.向下
y轴
(0,0)
探究点2:二次函数y=ax2的性质
问题1
从二次函数y=x2的图象可以看出:当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
问题2
从二次函数y=-x2的图象可以看出:当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
【自主归纳】
抛物线
y=ax2
(a>0)
y=ax2(a<0)
顶点坐标
(0,0)
(0,0)
对称轴
y轴
y轴
位置
第一、二象限
第三、四象限
开口方向
向上
向下
增减性
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
当x<0时,y随x的增大而增大;
当x>0时,y随x的增大而减小.
最值
最小值,为0
最大值,为0
【典例精析】例2
解:(1)由题意得S=(x>0).画函数图象略.
(2)点(4,2),(-4,1)不在该函数图象上,点(8,4)在该函数图象上.
例3解:
依题意有由①得m>-1,解②得m1=-2,m2=1,∴
m=1,此时,二次函数的表达式为
y=2x2.
【针对训练】
2
例4
<
<
y1>y2>y3
当堂检测
(0,0)
y轴
右
左
0
0
2.下方
增大
减小
0
≠
3.k>1
4.解:(1)把点A(2,-8)代入y=ax2,得-8=a×22,解得a=-2,则抛物线的表达式为y=-2x2;
(2)∵-2×32=-18,∴点B(3,-18)在该抛物线上;
(3)由题意得,-2x2=-50,解得x=±5,∴此抛物线上纵坐标是-50的点的坐标为(5,-50)、(-5,-50).
5.解:(1)画图象略;
(2)由图象可设该二次函数为y=ax2,将点(2,1)代入得4a=1,解得a=.则该二次函数的表达式为y=x2.
(3)
>
二次函数的图象与性质
1.
二次函数y=ax2的图象与性质
学习目标:
1.会用描点法画出二次函数y=ax2
的图象.(重点)
2.根据对特殊函数图象的观察,归纳得出二次函数y=ax2的性质.(难点)
3.进一步理解二次函数和抛物线的有关知识,并能解决一些简单的应用问题.
自主学习
知识链接
一次函数的图象是___________________,反比例函数的图象是_______________.
用描点法画函数图象的步骤:_______________、___________、__________.
下面是一次函数y=x-2的图象,根据图象,你能看出函数的哪些性质?
合作探究
要点探究
探究点1:二次函数y=ax2的图象
画一画
在同一直角坐标系中,画出函数y=2x2与y=-2x2的图象,并指出它们有何共同点?有何不同点?
列表如下:
x
…
-2
-1.5
-1
0
1
1.5
2
…
y=2x2
…
…
y=-2x2
…
…
(2)在如图所示的坐标系中,描点,连线:
(3)观察函数y=2x2与y=-2x2的图象,
写出它们的共同点(至少填写三条):
①:____________________________________________;
②:____________________________________________;
③:____________________________________________.
写出它们的不同点(至少填写三条):
①:____________________________________________;
②:____________________________________________;
③:____________________________________________.
【要点归纳】函数y=ax2的图象是一条抛物线,它是轴对称图形,对称轴是y轴(或直线x=0),抛物线与坐标轴的交点,叫做抛物线的顶点.其顶点坐标为(0,0).
【典例精析】
例1
在同一直角坐标系中,画出函数,的图象.
【针对训练】
在同一直角坐标系中,画出函数,的图象.
【要点归纳】对于抛物线
y
=
ax2,当a>0时,抛物线开口向上,对称轴是y轴,顶点是原点,顶点是抛物线的最低点;当a<0时,抛物线开口向下,对称轴是y轴,顶点是原点,顶点是抛物线的最高点;且|a|越大,抛物线的开口越小.
练一练
1.函数的图象的开口
,对称轴是
,顶点是
;
2.函数的图象的开口
,对称轴是
,顶点是
,顶点是抛物线的最
点;
探究点2:二次函数y=ax2的性质
观察与思考
图①
图②
问题1
如图①,观察二次函数y=x2的图象,y随x的变化如何变化?
问题2
如图②,观察二次函数y=-x2的图象,y随x的变化如何变化?
【自主归纳】?抛物线y=ax2的性质
抛物线
y=ax2
(a>0)
y=ax2(a<0)
顶点坐标
对称轴
位置
开口方向
增减性
最值
【典例精析】
例2
已知正方形周长为x
cm,面积为S
cm2.
(1)求S和x之间的函数关系式,并画出图象;
(2)判断点(4,2),(8,4),(-4,1)是否在该函数的图象上.
例3已知是二次函数,且其图象开口向上,求m的值和函数表达式.
【针对训练】已知是二次函数,且当x>0时,y随x增大而增大,则k=
.
例4
已知二次函数y=ax2.
若a=2,点(-2,y1)与(3,y2)在此二次函数的图象上,则y1_____
y2(填“>
”“=”或“<
”);
(2)若a>0,点(2,y1)与(3,y2)在此二次函数的图象上,则
y1_____
y2(填“>
”“=”或“<
”);
(3)若a<0,点(-2,y1)与(3,y2),(5,y3)在此二次函数的图象上,则y1,y2,y3的大小关系是___________.
方法总结:二次函数y=ax2中比较函数值的大小的方法:
①
直接代入法:将x的值分别代入函数表达式中,求出y值再比较大小,多用于a值确定的情况,如例4(1);
②性质判断法:结合二次函数的性质(增减性)及自变量x之间的大小关系,得出其对应y值的大小关系;多用于自变量x在对称轴同一侧的情况,如例4(2);
③草图法:画出二次函数的草图,描点,根据图象直接判断y值的大小.多用于a值不确定且x值不在对称轴同侧的情况,如例4(3).
二、课堂小结
二次函数y=ax2的图象及性质
画法
描点法→在对称轴两侧对称取点
图象
抛物线→轴对称图形
性质
1.开口方向及大小;
2.对称轴;
3.顶点坐标
4.增减性
当堂检测
1.抛物线y=5x2的顶点坐标是
,对称轴是
,在对称轴的
侧,y随着x的增大而增大;在对称轴的
侧,y
随着x的增大而减小,当x
=
时,函数y的值最小,最小值是
.
2.抛物线位置在x轴的
方(除顶点外),在对称轴的左侧,y随着x的增大而
;在对称轴的右侧,y随着x的增大而
,当x=0时,函数y的值最大,最大值是
,当x
0时,y<0.
3.如图,观察函数y=(k-1)x2的图象,则k的取值范围是
.
4.已知抛物线y=ax2的图象经过点A(2,-8),求:
(1)该抛物线的表达式;
(2)判断点B(3,-18)是否在该抛物线上;
(3)求出此抛物线上纵坐标是-50的点的坐标.
5.已知一个二次函数图象上部分点的横坐标x与纵坐标y的对应值如下表所示:
x
…
-4
-2
0
2
4
…
y
…
4
1
0
1
4
…
在给定的坐标系中,画出该二次函数的图象;
(2)求这个二次函数的表达式;
(3)若A(x1,y1),B(x2,y2)在这条抛物线上,且x1
参考答案
自主学习
知识链接
直线
双曲线
列表
描点
连线
解:①一次函数y=x-2的图象经过第一、三、四象限;②函数值y随x的增大而增大
合作探究
一、要点探究
探究点1:二次函数y=ax2的图象
画一画
(1)列表如下:
x
…
-2
-1.5
-1
0
1
1.5
2
…
y=2x2
…
8
4.5
2
0
2
4.5
8
…
y=-2x2
…
-8
-4.5
-2
0
-2
-4.5
-8
…
描点、连线如图①所示.
图①
图②
图③
相同点:①对称轴均为y轴
②顶点坐标均为(0,0)
③开口大小相同
不同点:①开口方向不同;
②y=2x2的图象有最低点,y=-2x2的图象有最高点;③当x<0时,y=2x2的图象呈下降趋势,y=-2x2的图象呈上升趋势
【典例精析】
例1
解:(1)列表如下:
x
…
-3
-1
0
1
3
…
y=x2
…
3
0
3
…
x
…
-2
-1
0
1
2
…
y=x2
…
4
1
0
1
4
…
描点、连线,如图②所示.
【针对训练】
解:(1)列表如下:
x
…
-3
-1
0
1
3
…
y=x2
…
-3
0
-3
…
x
…
-2
-1
0
1
2
…
y=-x2
…
-4
-1
0
-1
-4
…
描点、连线,如图③所示:
练一练
1.向上
y轴
(0,0)
2.向下
y轴
(0,0)
高
3.向上
y轴
(0,0)
低
4.向下
y轴
(0,0)
探究点2:二次函数y=ax2的性质
问题1
从二次函数y=x2的图象可以看出:当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
问题2
从二次函数y=-x2的图象可以看出:当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
【自主归纳】
抛物线
y=ax2
(a>0)
y=ax2(a<0)
顶点坐标
(0,0)
(0,0)
对称轴
y轴
y轴
位置
第一、二象限
第三、四象限
开口方向
向上
向下
增减性
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
当x<0时,y随x的增大而增大;
当x>0时,y随x的增大而减小.
最值
最小值,为0
最大值,为0
【典例精析】例2
解:(1)由题意得S=(x>0).画函数图象略.
(2)点(4,2),(-4,1)不在该函数图象上,点(8,4)在该函数图象上.
例3解:
依题意有由①得m>-1,解②得m1=-2,m2=1,∴
m=1,此时,二次函数的表达式为
y=2x2.
【针对训练】
2
例4
<
<
y1>y2>y3
当堂检测
(0,0)
y轴
右
左
0
0
2.下方
增大
减小
0
≠
3.k>1
4.解:(1)把点A(2,-8)代入y=ax2,得-8=a×22,解得a=-2,则抛物线的表达式为y=-2x2;
(2)∵-2×32=-18,∴点B(3,-18)在该抛物线上;
(3)由题意得,-2x2=-50,解得x=±5,∴此抛物线上纵坐标是-50的点的坐标为(5,-50)、(-5,-50).
5.解:(1)画图象略;
(2)由图象可设该二次函数为y=ax2,将点(2,1)代入得4a=1,解得a=.则该二次函数的表达式为y=x2.
(3)
>
