华东师大版九年级数学下册导学案:27.1.2 第1课时 圆的对称性
文档属性
| 名称 | 华东师大版九年级数学下册导学案:27.1.2 第1课时 圆的对称性 |

|
|
| 格式 | zip | ||
| 文件大小 | 890.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 22:51:19 | ||
图片预览


文档简介
27.1
圆的认识
2.圆的对称性
第1课时
圆的对称性
学习目标:
1.理解掌握圆的对称性.(重点)
2.运用圆的对称性研究圆心角、弧、弦之间的关系.(难点)
3.掌握圆心角、弧、弦之间的关系,并能加以应用.(难点)
自主学习
一、知识链接
1.已知△AOB,作出绕O点旋转45°,60°的图形.
2.如图,⊙O中有哪些圆心角,它们所对的弧分别是哪些弧,所对的弦又是哪些线段?
思考:能否通过圆心角之间的数量关系,得出弦长或弧长之间的数量关系呢?
二、新知预习
(预习教材P37-38)填空并完成练习:
在同一个圆中,如果圆心角相等,那么它们所对的_______相等,所对的弦________;
在同一个圆中,如果弧相等,那么它们所对的_______相等,所对的弦________;
在同一个圆中,如果弦相等,那么它们所对的_______相等,所对的弧________.
练习:.
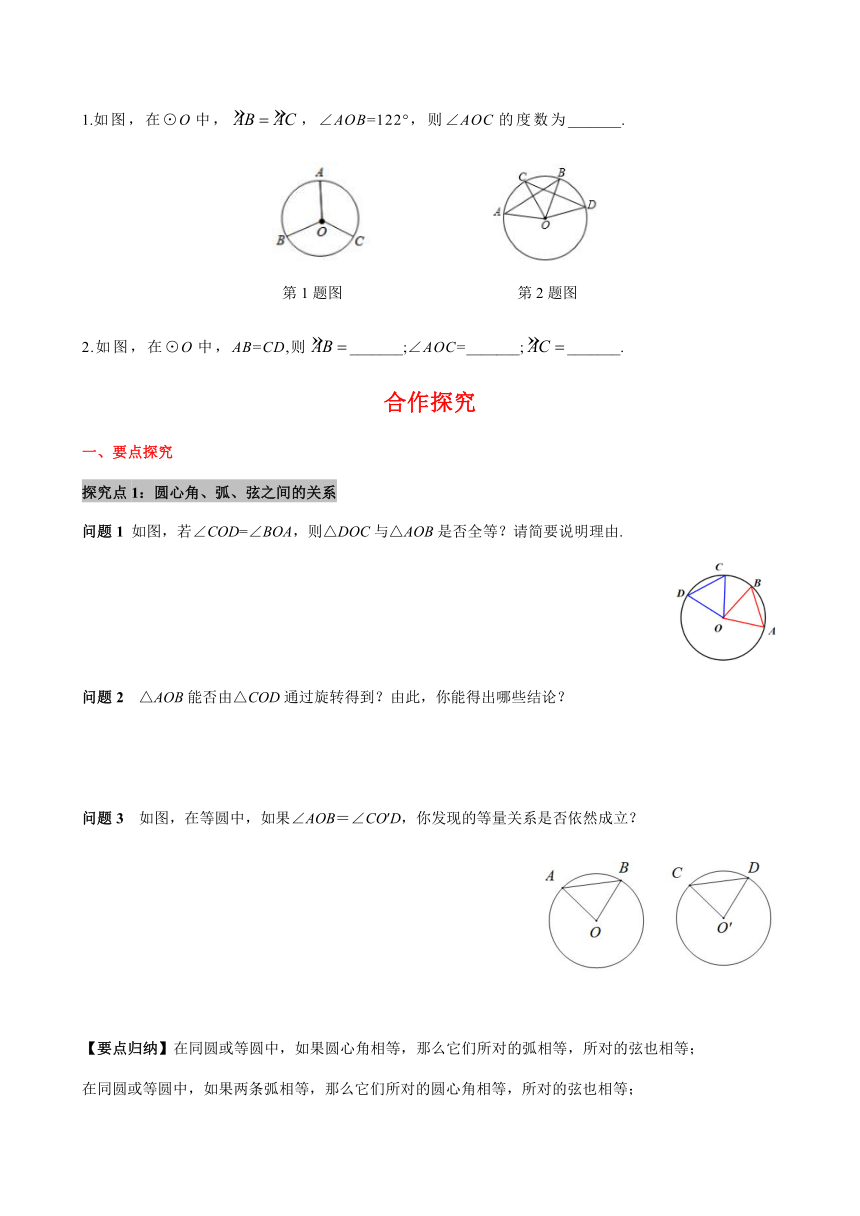
1.如图,在⊙O中,,∠AOB=122°,则∠AOC的度数为_______.
第1题图
第2题图
2.如图,在⊙O中,AB=CD,则_______;∠AOC=_______;_______.
合作探究
要点探究
探究点1:圆心角、弧、弦之间的关系
问题1
如图,若∠COD=∠BOA,则△DOC与△AOB是否全等?请简要说明理由.
问题2
△AOB能否由△COD通过旋转得到?由此,你能得出哪些结论?
问题3
如图,在等圆中,如果∠AOB=∠CO′D,你发现的等量关系是否依然成立?
【要点归纳】在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等;
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等;
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧也相等.
想一想:定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
【典例精析】
例1
如图,在⊙O中,,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
例2
如图,已知AB、CD为⊙O的两条弦,.求证:AB=CD.
【针对训练】
如图,在⊙O中,AD=BC,求证:DC=AB.
探究点2:圆的对称性
说一说:如图所示是一块圆心蛋糕,如何将它二等分、四等分、八等分?
做一做
剪一张圆心纸片,将其沿不同的方向对折,这些折痕有什么特点?
【要点归纳】圆是轴对称图形,它的任意一条直径所在的直线都是它的对称轴.圆有无数条对称轴.
二、课堂小结
弧、弦、圆心角
圆心角定义
顶点在圆心的角
弧、弦、圆心角的关系定理及推论
在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等;
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等;
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧也相等.
圆的对称性
圆是_____对称图形,它的任意一条直径所在的直线都是它的__________.
当堂检测
如图,在⊙O中,,∠1=45°,则∠2=( )
A.60°
B.30°
C.45°
D.40°
第1题图
第2题图
2.如图,在⊙O中,∠AOB=40°,则∠COD的度数( )
A.20°
B.40°
C.50°
D.60°
3.如图,已知,∠BAC=50°,求∠B的度数.
4.如图,AB
是⊙O
的直径,,∠COD=40°,求∠AOE
的度数.
5.如图,AB为⊙O的直径,C、D是⊙O上的两点,且BD∥OC,求证:.
参考答案
自主学习
知识链接
解:图略.
⊙O中的圆心角有∠AOB、∠AOC、∠AOD、∠BOC、∠BOD、∠COD;∠AOB所对的弦为线段AB,所对的弧为;∠AOC所对的弧为;∠AOD所对的弧为;∠BOC所对的弧为;∠BOD所对的弧为;∠COD所对的弦为线段CD,所对的弧为.
新知预习
(1)弧
相等
(2)圆心角
相等
(3)圆心角
相等
练习:
1.122°
2.
∠BOD
合作探究
一、要点探究
探究点1:圆心角、弧、弦之间的关系
问题1
解:△DOC与△AOB全等,理由如下:由圆的定义可知DO=CO=BO=AO,∵∠COD=∠BOA,∴△DOC≌△AOB.
问题2
能
AB=CD
=
问题3
依然成立.
想一想
不能去掉;如图,显然>,弦AB>弦CD,所以不能去掉.
【典例精析】例1
证明:∵,∴
AB=AC.∴△ABC是等腰三角形.又∵∠ACB=60°,∴△ABC是等边三角形,AB=BC=CA.∴∠AOB=∠BOC=∠AOC.
例2
证明:∵,∴∴.∴AB=CD.
【针对训练】证明:∵AD=BC,∴.∴∴∴DC=AB.
探究点2:圆的对称性
说一说
沿着过中心的一条直线切一刀,即可将蛋糕2等分;沿着过中心且与第一刀垂直的方向切第二刀,可将蛋糕四等分;沿着圆心处形成的直角的平分线切两刀,可将蛋糕八等分.
做一做
所有折痕交于一点,这一点为圆心.
二、课堂小结
轴
对称轴
当堂检测
1.C
2.B
3.解:∵,∴AB=AC.∵∠BAC=50°,∴∠B=(180°-∠BAC)=65°.
4.解:∵,∴∠BOC=∠COD=∠DOE=40°,∴∠AOE=180°-3×40°=60°.
5.证明:∵OB=OD,∴∠D=∠B.∵BD∥OC,∴∠D=∠COD,∠AOC=∠B,∴∠AOC=∠COD,∴
圆的认识
2.圆的对称性
第1课时
圆的对称性
学习目标:
1.理解掌握圆的对称性.(重点)
2.运用圆的对称性研究圆心角、弧、弦之间的关系.(难点)
3.掌握圆心角、弧、弦之间的关系,并能加以应用.(难点)
自主学习
一、知识链接
1.已知△AOB,作出绕O点旋转45°,60°的图形.
2.如图,⊙O中有哪些圆心角,它们所对的弧分别是哪些弧,所对的弦又是哪些线段?
思考:能否通过圆心角之间的数量关系,得出弦长或弧长之间的数量关系呢?
二、新知预习
(预习教材P37-38)填空并完成练习:
在同一个圆中,如果圆心角相等,那么它们所对的_______相等,所对的弦________;
在同一个圆中,如果弧相等,那么它们所对的_______相等,所对的弦________;
在同一个圆中,如果弦相等,那么它们所对的_______相等,所对的弧________.
练习:.
1.如图,在⊙O中,,∠AOB=122°,则∠AOC的度数为_______.
第1题图
第2题图
2.如图,在⊙O中,AB=CD,则_______;∠AOC=_______;_______.
合作探究
要点探究
探究点1:圆心角、弧、弦之间的关系
问题1
如图,若∠COD=∠BOA,则△DOC与△AOB是否全等?请简要说明理由.
问题2
△AOB能否由△COD通过旋转得到?由此,你能得出哪些结论?
问题3
如图,在等圆中,如果∠AOB=∠CO′D,你发现的等量关系是否依然成立?
【要点归纳】在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等;
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等;
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧也相等.
想一想:定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
【典例精析】
例1
如图,在⊙O中,,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
例2
如图,已知AB、CD为⊙O的两条弦,.求证:AB=CD.
【针对训练】
如图,在⊙O中,AD=BC,求证:DC=AB.
探究点2:圆的对称性
说一说:如图所示是一块圆心蛋糕,如何将它二等分、四等分、八等分?
做一做
剪一张圆心纸片,将其沿不同的方向对折,这些折痕有什么特点?
【要点归纳】圆是轴对称图形,它的任意一条直径所在的直线都是它的对称轴.圆有无数条对称轴.
二、课堂小结
弧、弦、圆心角
圆心角定义
顶点在圆心的角
弧、弦、圆心角的关系定理及推论
在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等;
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等;
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧也相等.
圆的对称性
圆是_____对称图形,它的任意一条直径所在的直线都是它的__________.
当堂检测
如图,在⊙O中,,∠1=45°,则∠2=( )
A.60°
B.30°
C.45°
D.40°
第1题图
第2题图
2.如图,在⊙O中,∠AOB=40°,则∠COD的度数( )
A.20°
B.40°
C.50°
D.60°
3.如图,已知,∠BAC=50°,求∠B的度数.
4.如图,AB
是⊙O
的直径,,∠COD=40°,求∠AOE
的度数.
5.如图,AB为⊙O的直径,C、D是⊙O上的两点,且BD∥OC,求证:.
参考答案
自主学习
知识链接
解:图略.
⊙O中的圆心角有∠AOB、∠AOC、∠AOD、∠BOC、∠BOD、∠COD;∠AOB所对的弦为线段AB,所对的弧为;∠AOC所对的弧为;∠AOD所对的弧为;∠BOC所对的弧为;∠BOD所对的弧为;∠COD所对的弦为线段CD,所对的弧为.
新知预习
(1)弧
相等
(2)圆心角
相等
(3)圆心角
相等
练习:
1.122°
2.
∠BOD
合作探究
一、要点探究
探究点1:圆心角、弧、弦之间的关系
问题1
解:△DOC与△AOB全等,理由如下:由圆的定义可知DO=CO=BO=AO,∵∠COD=∠BOA,∴△DOC≌△AOB.
问题2
能
AB=CD
=
问题3
依然成立.
想一想
不能去掉;如图,显然>,弦AB>弦CD,所以不能去掉.
【典例精析】例1
证明:∵,∴
AB=AC.∴△ABC是等腰三角形.又∵∠ACB=60°,∴△ABC是等边三角形,AB=BC=CA.∴∠AOB=∠BOC=∠AOC.
例2
证明:∵,∴∴.∴AB=CD.
【针对训练】证明:∵AD=BC,∴.∴∴∴DC=AB.
探究点2:圆的对称性
说一说
沿着过中心的一条直线切一刀,即可将蛋糕2等分;沿着过中心且与第一刀垂直的方向切第二刀,可将蛋糕四等分;沿着圆心处形成的直角的平分线切两刀,可将蛋糕八等分.
做一做
所有折痕交于一点,这一点为圆心.
二、课堂小结
轴
对称轴
当堂检测
1.C
2.B
3.解:∵,∴AB=AC.∵∠BAC=50°,∴∠B=(180°-∠BAC)=65°.
4.解:∵,∴∠BOC=∠COD=∠DOE=40°,∴∠AOE=180°-3×40°=60°.
5.证明:∵OB=OD,∴∠D=∠B.∵BD∥OC,∴∠D=∠COD,∠AOC=∠B,∴∠AOC=∠COD,∴
