七年级数学下册苏科版第十一章第六课《一元一次不等式组(一)》教案
文档属性
| 名称 | 七年级数学下册苏科版第十一章第六课《一元一次不等式组(一)》教案 |  | |
| 格式 | doc | ||
| 文件大小 | 118.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 22:16:19 | ||
图片预览


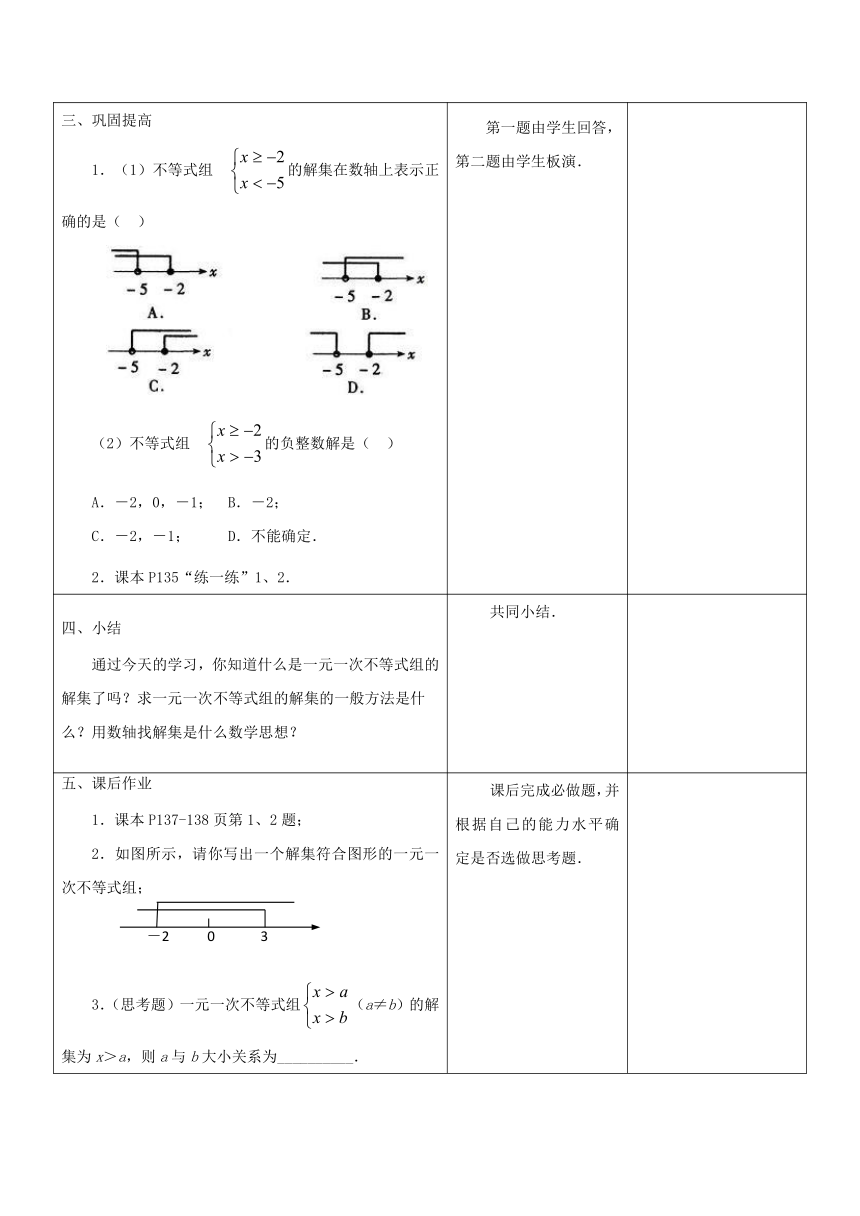
文档简介
11.6 一元一次不等式组
11.6 一元一次不等式组(1)
教学目标 1.知道什么是一元一次不等式组;
2.理解一元一次不等式组解集的概念,会利用数轴解简单的一元一次不等式组.
3.借助数轴掌握一元一次不等式组解集的几种情况,渗透用数学图形解题的直观性、简捷性的数学美.
教学重点 借助数轴求一元一次不等式组解集.
教学难点 一元一次不等式组解集的概念.
教学过程(教师) 学生活动 二次备课
一、情境引入 小丽早晨7时30分骑自行车上学,要在7时50分至7时55分之间到达离家3400m的学校,小丽骑自行车的速度应在什么范围内?
(1)如果设小丽骑自行车的速度为x m/min.你可以列出几个不等式? 学生积极思考、回忆旧知,会列出这样的不等式.
(2)所列的几个不等式有什么相同之处? 学生会说出许多相似之处,如都是不等式,都含有3400,都有一个未知数,未知数都代表同一个意思等.
二、讲授新课 (1)讲一讲:
不等式解集的概念:这时有未知数x 同时满足两个不等式,把这两个不等式联立在一起,可以记作.
像这样,把几个含有同一个未知数的一次不等式联立在一起,就组成了一个一元一次不等式组. 理解、记忆.
(2)议一议:如何找出使①与②都成立的未知数x的值? 问题1 如何在数轴上表示使不等式
成立的未知数x的值?
问题2 如何在数轴上表示使不等式
成立的未知数x的值?
问题3 观察所画图形,使不等式、
都成立的未知数x的值有多少个?
不等式组的解集的概念:不等式组中所有不等式解集的公共部分,叫做不等式组的解集.
解不等式组的概念:求不等式组的解集的过程叫做解不等式组. 学生在同一个数轴上把两个不等式的解集分别表示出来后,观察图形回答议一议的问题.
(3)例题1 利用数轴确定不等式组的解集. 学生跟随老师共同完成.
(4)练一练:利用数轴确定下列不等式组的解集 ①不等式组的解集是 ;
②不等式组的解集是 ;
③不等式组的解集是 ;
④不等式组的解集是 . 学生独立完成.
(5)例题2:利用数轴确定不等式组的解集. 学生独立完成.
三、巩固提高 1.(1)不等式组?的解集在数轴上表示正确的是( )
?
(2)不等式组?的负整数解是( )
A.-2,0,-1; B.-2;
C.-2,-1; D.不能确定.
2.课本P135“练一练”1、2. 第一题由学生回答,第二题由学生板演.
四、小结 通过今天的学习,你知道什么是一元一次不等式组的解集了吗?求一元一次不等式组的解集的一般方法是什么?用数轴找解集是什么数学思想? 共同小结.
五、课后作业 1.课本P137-138页第1、2题;
2.如图所示,请你写出一个解集符合图形的一元一次不等式组;
3.(思考题)一元一次不等式组(a≠b)的解集为x>a,则a与b大小关系为__________. 课后完成必做题,并根据自己的能力水平确定是否选做思考题.
11.6 一元一次不等式组(2)
教学目标 1.会利用数轴求一元一次不等式组的解集,并归纳一般步骤;
2.了解一元一次不等式组无解的情况;
3.会利用不等式组解决一些简单的实际问题;
4.加深学生对数形结合的作用的理解,让学生体会数学解题的直观性和简洁性的数学美.
教学重点 不等式组的解法及其步骤.
教学难点 列不等式组解决一些简单的实际问题.
教学过程(教师) 学生活动 二次备课
一、情境引入 1.利用数轴求不等式组的解集.
2.利用数轴求不等式组的解集.
3.利用数轴求不等式组的解集. 学生黑板板演.
二、讲授新课 例题1 解不等式组.
(1)
(2)
一元一次不等式组的两个步骤:
(1)求出这个不等式组中各个不等式的解集;
(2)利用数轴求出这些不等式的解集的公共部分,即求出这个不等式组的解集. 学生先做第一题,然后由师生共同总结解一元一次不等式组的一般步骤,再接着做第二题.
练一练:解下列不等式组. (1)
(2)
(3) 学生独立完成.
试一试: 当代数式2x-1的值大于-3且小于1时,求x的取值范围. 让学生先进行讨论,然后再请学生上黑板板演,其他学生在下面做.
三、巩固提高 课本P137“练一练”1、2. 学生板演,互相批改,发现问题,及时投影.
四、小结 1.一元一次不等式组有无解集的标志是什么?
2.如何解一元一次不等式组?
3.你能归纳出含两个相同求知数的一元一次不等式组成的不等式组解集的特点吗? 共同小结.
五、课后作业 1.课本P138页3、4、5.
2.思考题:
已知关于x的不等式组 无解,求a的取值范围. 课后完成必做题,并根据自己的能力水平确定是否选做思考题.
11.6 一元一次不等式组(1)
教学目标 1.知道什么是一元一次不等式组;
2.理解一元一次不等式组解集的概念,会利用数轴解简单的一元一次不等式组.
3.借助数轴掌握一元一次不等式组解集的几种情况,渗透用数学图形解题的直观性、简捷性的数学美.
教学重点 借助数轴求一元一次不等式组解集.
教学难点 一元一次不等式组解集的概念.
教学过程(教师) 学生活动 二次备课
一、情境引入 小丽早晨7时30分骑自行车上学,要在7时50分至7时55分之间到达离家3400m的学校,小丽骑自行车的速度应在什么范围内?
(1)如果设小丽骑自行车的速度为x m/min.你可以列出几个不等式? 学生积极思考、回忆旧知,会列出这样的不等式.
(2)所列的几个不等式有什么相同之处? 学生会说出许多相似之处,如都是不等式,都含有3400,都有一个未知数,未知数都代表同一个意思等.
二、讲授新课 (1)讲一讲:
不等式解集的概念:这时有未知数x 同时满足两个不等式,把这两个不等式联立在一起,可以记作.
像这样,把几个含有同一个未知数的一次不等式联立在一起,就组成了一个一元一次不等式组. 理解、记忆.
(2)议一议:如何找出使①与②都成立的未知数x的值? 问题1 如何在数轴上表示使不等式
成立的未知数x的值?
问题2 如何在数轴上表示使不等式
成立的未知数x的值?
问题3 观察所画图形,使不等式、
都成立的未知数x的值有多少个?
不等式组的解集的概念:不等式组中所有不等式解集的公共部分,叫做不等式组的解集.
解不等式组的概念:求不等式组的解集的过程叫做解不等式组. 学生在同一个数轴上把两个不等式的解集分别表示出来后,观察图形回答议一议的问题.
(3)例题1 利用数轴确定不等式组的解集. 学生跟随老师共同完成.
(4)练一练:利用数轴确定下列不等式组的解集 ①不等式组的解集是 ;
②不等式组的解集是 ;
③不等式组的解集是 ;
④不等式组的解集是 . 学生独立完成.
(5)例题2:利用数轴确定不等式组的解集. 学生独立完成.
三、巩固提高 1.(1)不等式组?的解集在数轴上表示正确的是( )
?
(2)不等式组?的负整数解是( )
A.-2,0,-1; B.-2;
C.-2,-1; D.不能确定.
2.课本P135“练一练”1、2. 第一题由学生回答,第二题由学生板演.
四、小结 通过今天的学习,你知道什么是一元一次不等式组的解集了吗?求一元一次不等式组的解集的一般方法是什么?用数轴找解集是什么数学思想? 共同小结.
五、课后作业 1.课本P137-138页第1、2题;
2.如图所示,请你写出一个解集符合图形的一元一次不等式组;
3.(思考题)一元一次不等式组(a≠b)的解集为x>a,则a与b大小关系为__________. 课后完成必做题,并根据自己的能力水平确定是否选做思考题.
11.6 一元一次不等式组(2)
教学目标 1.会利用数轴求一元一次不等式组的解集,并归纳一般步骤;
2.了解一元一次不等式组无解的情况;
3.会利用不等式组解决一些简单的实际问题;
4.加深学生对数形结合的作用的理解,让学生体会数学解题的直观性和简洁性的数学美.
教学重点 不等式组的解法及其步骤.
教学难点 列不等式组解决一些简单的实际问题.
教学过程(教师) 学生活动 二次备课
一、情境引入 1.利用数轴求不等式组的解集.
2.利用数轴求不等式组的解集.
3.利用数轴求不等式组的解集. 学生黑板板演.
二、讲授新课 例题1 解不等式组.
(1)
(2)
一元一次不等式组的两个步骤:
(1)求出这个不等式组中各个不等式的解集;
(2)利用数轴求出这些不等式的解集的公共部分,即求出这个不等式组的解集. 学生先做第一题,然后由师生共同总结解一元一次不等式组的一般步骤,再接着做第二题.
练一练:解下列不等式组. (1)
(2)
(3) 学生独立完成.
试一试: 当代数式2x-1的值大于-3且小于1时,求x的取值范围. 让学生先进行讨论,然后再请学生上黑板板演,其他学生在下面做.
三、巩固提高 课本P137“练一练”1、2. 学生板演,互相批改,发现问题,及时投影.
四、小结 1.一元一次不等式组有无解集的标志是什么?
2.如何解一元一次不等式组?
3.你能归纳出含两个相同求知数的一元一次不等式组成的不等式组解集的特点吗? 共同小结.
五、课后作业 1.课本P138页3、4、5.
2.思考题:
已知关于x的不等式组 无解,求a的取值范围. 课后完成必做题,并根据自己的能力水平确定是否选做思考题.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
