高中数学人教A版新课标必修1第三章3.4函数的应用(一)练习题-(Word含解析)
文档属性
| 名称 | 高中数学人教A版新课标必修1第三章3.4函数的应用(一)练习题-(Word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 140.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 00:00:00 | ||
图片预览




文档简介
高中数学人教A版新课标必修1第三章3.4函数的应用(一)练习题
一、选择题
生产一定数量的商品的全部费用称为生产成本,某企业一个月生产某种商品x万件时的生产成本为万元一万件售价是20万元,为获取更大利润,该企业一个月应生产该商品数量为
A.
36万件
B.
18万件
C.
22万件
D.
9万件
德国著名数学家狄利克雷在数学领域成就显著,以其名字命名的函数被称为狄利克雷函数,其中R为实数集,Q为有理数集,则关于狄利克雷函数给出四个命题:?
;函数是偶函数;任取一个不为零的有理数T,对任意的恒成立;存在三个点,,,使得为等边三角形.其中真命题的个数是???
A.
1
B.
2
C.
3
D.
4
某手机生产线的年固定成本为250万元,每生产x千台需另投入成本万元.当年产量不足80千台时,万元;当年产量不小于80千台时,万元,每千台产品的售价为50万元,该厂生产的产品能全部售完.当年产量为??????
千台时,该厂当年的利润最大?
A.
60
B.
80
C.
100
D.
120
某商店计划投入资金20万元经销甲或乙商品,已知经销甲商品与乙商品所获得的利润分别为P和万元,且它们与投入资金万元的关系是:,若不管资金如何投放,经销这两种商品或其中一种商品所获得的纯利润总不少于5万元,则a的最小值为?
A.
B.
5
C.
D.
某公司生产一种产品,固定成本为元,每生产一单位的产品,成本增加100元,若总收入R与年产量x的关系是则当总利润最大时,每年生产产品的单位数是?
?
A.
150
B.
200
C.
250
D.
300
若为偶函数,且当时,,则当时有
A.
B.
C.
D.
德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数被称为狄利克雷函数,其中R为实数集,Q为有理数集,则关于函数有如下四个命题:;函数是偶函数;任取一个不为零的有理数T,对任意的恒成立;存在三个点,,,使得为等边三角形.其中真命题的个数有
A.
1个
B.
2个
C.
3个
D.
4个
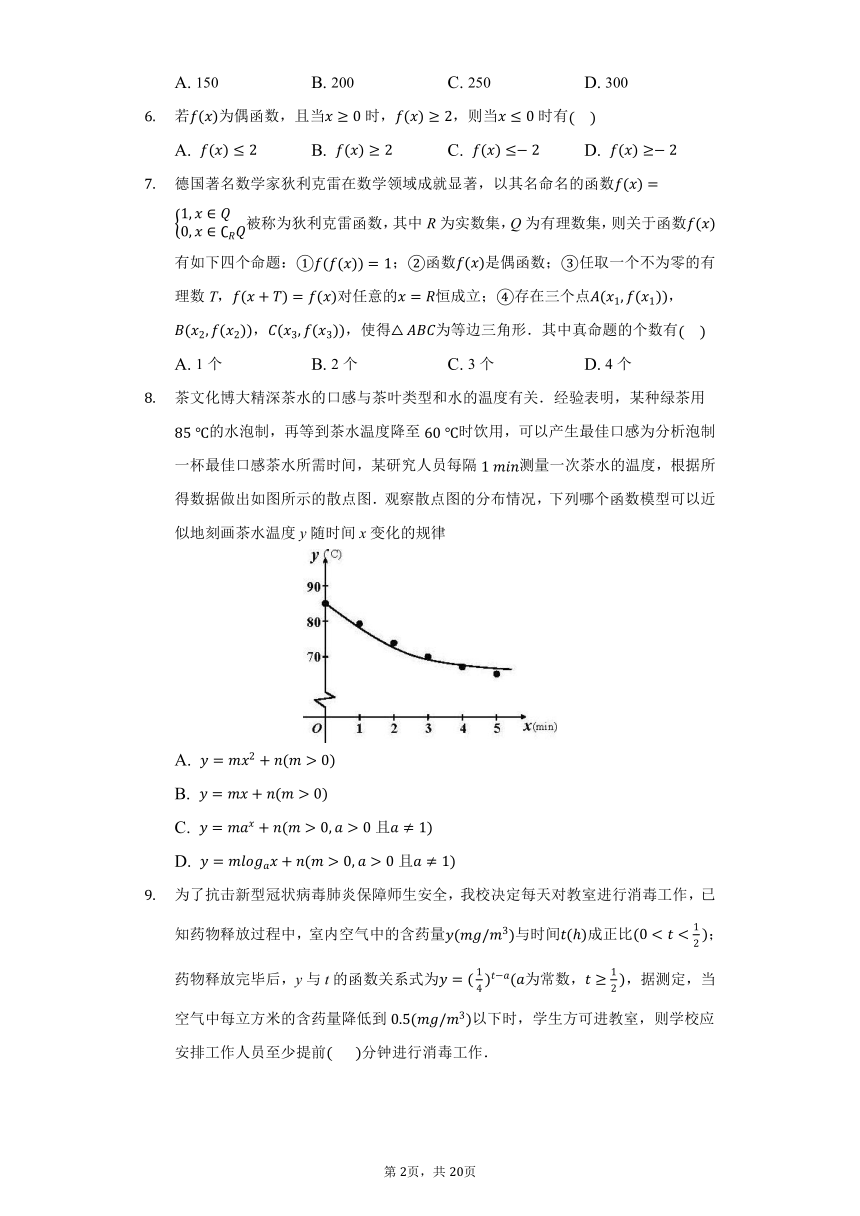
茶文化博大精深茶水的口感与茶叶类型和水的温度有关.经验表明,某种绿茶用的水泡制,再等到茶水温度降至时饮用,可以产生最佳口感为分析泡制一杯最佳口感茶水所需时间,某研究人员每隔测量一次茶水的温度,根据所得数据做出如图所示的散点图.观察散点图的分布情况,下列哪个函数模型可以近似地刻画茶水温度y随时间x变化的规律
A.
B.
C.
且
D.
且
为了抗击新型冠状病毒肺炎保障师生安全,我校决定每天对教室进行消毒工作,已知药物释放过程中,室内空气中的含药量与时间成正比;药物释放完毕后,y与t的函数关系式为为常数,,据测定,当空气中每立方米的含药量降低到以下时,学生方可进教室,则学校应安排工作人员至少提前?
?
分钟进行消毒工作.
A.
30
B.
40
C.
60
D.
90
某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为其中x代表拟录用人数,y代表面试人数.若面试人数为60,则该公司拟录用人数为
A.
15
B.
25
C.
40
D.
130
二、不定项选择题
“双11”购物节中,某电商对顾客实行购物优惠活动,规定一次购物付款总额满一定额度,可以给予优惠:
如果购物总额不超过50元,则不给予优惠;
如果购物总额超过50元但不超过100元,可以使用一张5元优惠券;
如果购物总额超过100元但不超过300元,则按标价给予9折优惠;
如果购物总额超过300元,其中300元内的按第条给予优惠,超过300元的部分给予8折优惠.某人购买了部分商品,则下列说法正确的是?
?
A.
如果购物总额为78元,则应付款为73元
B.
如果购物总额为228元,则应付款为元
C.
如果购物总额为368元,则应付款为元
D.
如果购物时一次性全部付款元,则购物总额为516元
某工厂生产某种产品的年固定成本为200万元,每生产x千件,需另投入成本为y万元,当年产量不足80千件时,,当年产量不小于80千件时,每件商品售价为万元,年利润为通过市场分析,该厂生产的商品能全部售完,则下列选项正确的是
A.
年利润和年产量的关系为
B.
年利润和年产量的关系为
C.
年利润最大为1050万元
D.
年利润最大为1450万元
甲同学家到乙同学家的途中有一座公园,甲同学家到公园的距离与乙同学家到公园的距离都是如图所示表示甲同学从家出发到乙同学家经过的路程与时间的关系,下列结论正确的是
A.
甲同学从家出发到乙同学家走了
B.
甲从家到公园的时间是
C.
甲从家到公园的速度比从公园到乙同学家的速度快
D.
当时,y与x的关系式为
E.
当时,y与x的关系式为
某停车场的收费标准如下:临时停车半小时内含半小时免费,临时停车1小时收费5元,此后每停车1小时收费3元,不足1小时按1小时计算,24小时内最高收费40元.现有甲、乙两车临时停放在该停车场,下列判断正确的是
A.
若甲车与乙车的停车时长之和为小时,则停车费用之和可能为8元
B.
若甲车与乙车的停车时长之和为小时,则停车费用之和可能为10元
C.
若甲车与乙车的停车时长之和为10小时,则停车费用之和可能为34元
D.
若甲车与乙车的停车时长之和为25小时,则停车费用之和可能为45元
三、填空题
已知函数,若a,b,c互不相等,且,则的取值范围为______用区间表示
设函数,函数,若存在唯一的,使得的值为,则实数a的取值范围为______.
已知函数,若?
互不相等,且的取值范围为,则实数m的值为__________________.
设函数若,则______.
四、解答题
某公司为提高员工的综合素质,聘请专业机构对员工进行专业技术培训,其中培训机构成本费用为元.公司每位员工的培训费用按以下方式与该机构结算:若公司参加培训的员工人数不超过30,则每人的培训费用为850元;若公司参加培训的员工人数多于30,则给予优惠:每多一人,每位员工的培训费减少10元.已知该公司最多有60位员工可参加培训,设参加培训的员工人数为x,每位员工的培训费用为y元,培训机构的利润为Q元.
写出y与之间的函数关系式;
当公司参加培训的员工为多少人时,培训机构可获得最大利润?并求最大利润.
某工厂某种产品的年固定成本为250万元,每生产x件,需另投入成本万元,当年产量不足80件时,,当年产量不少于80件时,,每件产品的售价为50万元,通过市场分析,该厂生产的产品能全部售完.
写出年利润万元关于年产量件的函数关系式;
当年产量为多少件时,该厂在这一产品的生产中所获利润最大?
习总书记指出:“绿水青山就是金山银山”常州市一乡镇响应号召,因地制宜的将该镇打造成“生态水果特色小镇”调研过程中发现:某珍稀水果树的单株产量单位:千克与肥料费用单位:元满足如下关系:其它成本投入如培育管理等人工费为单位:元已知这种水果的市场售价大约为10元千克,且供不应求.记该单株水果树获得的利润为单位:元.
求的函数关系式;
当投入的肥料费用为多少时,该单株水果树获得的利润最大最大利润是多少
某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足如下函数:其中x是仪器的产量.
将利润表示为产量x的函数利润总收益总成本
当产量x为何值时,公司所获利润最大?最大利润是多少元?
?为响应国家提出的“大众创业,万众创新”的号召,小王同学大学毕业后,决定利用所学专业进行自主创业.经过市场调查,生产某小型电子产品需投入年固定成本为2万元,每生产x万件,需另投入流动成本为万元.在年产量不足8万件时,万元;在年产量不小于8万件时,万元每年产品售价为6元.假设小王生产的商品当年全部售完.
??
写出年利润万元关于年产量万件的函数解析式注:年利润年销售收入固定成本流动成本;
??
年产量为多少万件时,小王在这一商品的生产中所获利润最大?最大利润是多少?
答案和解析
1.【答案】B
【解析】
【分析】
本题考查二次函数模型、二次函数的最值.根据题意,得利润函数,利用二次函数的性质,分析求得答案.
【解答】
解:根据题意,利润函数为:
,
当时,有最大值.
故选B.
2.【答案】C
【解析】
【分析】
根据函数的对应法则,可得不管x是有理数还是无理数,均有;根据函数奇偶性的定义,可得是偶函数;根据函数的表达式,结合有理数和无理数的性质可得;取,,,可得,,,三点恰好构成等边三角形.
本题给出特殊函数表达式,求函数的值并讨论它的奇偶性,着重考查了有理数、无理数的性质和函数的奇偶性等知识,属于中档题.
【解答】
解:当x为有理数时,;当x为无理数时,
当x为有理数时,;当x为无理数时,
即不管x是有理数还是无理数,均有,故不正确;
有理数的相反数还是有理数,无理数的相反数还是无理数,
对任意,都有,故正确;
若x是有理数,则也是有理数;若x是无理数,则也是无理数
根据函数的表达式,任取一个不为零的有理数T,对恒成立,故正确;
取,,,可得,,
,,,恰好为等边三角形,故正确.
故选C.
3.【答案】C
【解析】
【分析】
本题考查分段函数模型,函数的应用,属于中档题.
求出利润的函数解析式,用分段函数表示,然后分段求出函数的最大值,比较大小求解即可.
【解答】
解:?设年产量为x千台,当年的利润为y万元,
则由已知有
即
当时,由二次函数知当时,y取得最大值950,
当时,y在单调递增,在单调递减,所以当时,y取得最大值1000,
又,
所以当年产量为100千台时,该厂当年的利润取得最大值1000万元.
故选C.
4.【答案】A
【解析】
【分析】
本题考查函数最值的运用,考查学生利用数学知识解决实际问题,考查学生分析解决问题的能力,属于中档题.
设投资甲商品万元,则投资乙商品x万元,由题意,可得,时恒成立,化简求最值,即可得到结论.
【解答】
解:设投资甲商品万元,则投资乙商品x万元,
利润分别为,
时恒成立,
当时,a为一切实数
当时,分离参数得,时恒成立,
?,?
,
,
综上可得:.
所以a的最小值为,
故选A.
5.【答案】D
【解析】
【试题解析】
【分析】
本题主要考查分段函数模型的应用应用导数求实际问题中的最值问题.
根据题意得出总利润的表达式,然后利用求导得出最值得条件.
【解答】
解:由题意得,总利润?
当时,,
令,得舍负,
当时,,函数单调递增,当时,,函数单调递减,
故当时,在上取得最大值,
又当时,为减函数,
所以当每年生产300单位的产品时,总利润最大,
故选D.
6.【答案】B
【解析】
【分析】本题考查了函数的奇偶性的相关知识,试题难度较易
【解答】解:当时,,,所以,所以当时,.
故选B.
7.【答案】D
【解析】解:当x为有理数时,;当x为无理数时,
当x为有理数时,;
当x为无理数时,
即不管x是有理数还是无理数,均有,故正确;
有理数的相反数还是有理数,无理数的相反数还是无理数,
对任意,都有,故正确;
若x是有理数,则也是有理数;若x是无理数,则也是无理数
根据函数的表达式,任取一个不为零的有理数T,对恒成立,故正确;
取,,,可得,,
,,,恰好为等边三角形,故正确.
故选:D.
根据函数的对应法则,可得不管x是有理数还是无理数,均有;根据函数奇偶性的定义,可得是偶函数;根据函数的表达式,结合有理数和无理数的性质;取,,,可得,,,三点恰好构成等边三角形.
本题给出特殊函数表达式,求函数的值并讨论它的奇偶性,着重考查了有理数、无理数的性质和函数的奇偶性等知识,属于中档题.
8.【答案】C
【解析】
【分析】
本题考查函数模型的应用,属于基础题.根据散点图结合各选项中函数模型即可得出结果.
【解答】
解:选项A中,函数的图象以y轴为对称轴,不符散点图;
选项B中,函数的图象是直线,不符散点图;
选项D中,,与y轴无限接近,与散点图不符.
故选C.
9.【答案】C
【解析】
【分析】
本题考查分段函数模型,函数图像的应用,属于基础题.
由已知条件求出室内空气中的含药量关于时间的函数解析式,即可得解.
【解答】
解:根据图像:函数过点,故,
当时,取,解得,1小时分钟.
故选:C.
10.【答案】B
【解析】
【分析】本题考查了分段函数的相关知识,试题难度较易
【解答】解:令,若,则,不合题意;
若,则,满足题意;
若,则,不合题意.
故该公司拟录用25人.
11.【答案】ABD
【解析】
【试题解析】
【分析】
本题考查函数模型的应用,属于基础题.
结合购物总额对应哪种情况进行计算即可.
【解答】
解:对于A项,购物总额为78元,属于情况,可以使用一张5元优惠劵,则应付款为元,故A项正确
对于B项,购物总额为228元,属于情况,则按标价给予9折优惠,
则应付款为元,故B项正确
对于C项,购物总额为368元,属于情况,则其中300元内的按第条给予优惠,超过300元的部分给予8折优惠,故应付款为元,故C项错误
对于D项,若购物时一次性全部付款元,属于情况,
设超过300元的部分为x元,
则,解得元,则购物总额为元,故D项正确.
故选ABD.
12.【答案】AC
【解析】
【试题解析】
【分析】
本题考查分段函数模型的应用,考查二次函数以及基本不等式的应用,属于中档题.
利用条件可分别求出当80和时,万元关于年产量千件的函数解析式,利用二次函数的最值以及基本不等式,分段求解函数的最值,进而可得到结果.
【解答】
解:因为每件商品售价为万元,则x千件商品销售额为万元,依题意得:
当时,.
当时,
所以.
当时,.
此时,当时,z取得最大值万元.
当时,,
此时,即时,z取得最大值万元.
由于,
所以当年产量为100千件时,该厂在这一商品生产中所获利润最大,最大利润为1050万元.
故选AC.
13.【答案】BD
【解析】
【分析】本题考查了函数图象的应用的相关知识,试题难度较易
【解答】解:在A中,甲在公园休息的时间是,所以只走了,A错误;
由题中图象知B正确;
甲从家到公园所用的时间比从公园到乙同学家所用的时间长,而距离相等,所以甲从家到公园的速度比从公园到乙同学家的速度慢,C错误;
当时,设,则,解得,D正确;
当时,题中图象是平行于x轴的线段,E错误.
故选BD.
14.【答案】ACD
【解析】
【分析】
本题考查分段函数模型的应用,属于基础题.
根据题设中数据,即可计算出各选项的正误.
【解答】
解:若甲车停车小时,乙车停车小时,则停车费用之和为8元,A正确;
若甲车与乙车的停车时长之和为小时,则停车费用之和可能为8元或13元或16元,B错误;
若甲车与乙车都停车5小时,则停车费用之和为34元,C正确;
若甲车停车24小时,乙车停车1小时,则停车费用之和为45元,D正确.
故选ACD.
15.【答案】
【解析】解:作出函数,的图象,
不妨设,,,
,
由题意可知,
故而解得,
,
令,,则在递减,,,
,
的取值范围为,
故答案为:
先画出图象,再根据条件即可求出其范围.不妨设,利用,可得,,再构造函数,由此可确定的取值范围.
本题考查分段函数,考查绝对值函数,考查学生分析解决问题的能力,属于中档题.
16.【答案】
【解析】解:作出函数的图象,
可得的最小值为0,最大值为2;
,
当且仅当取得最小值.
由存在唯一的,使得的值
为,
可得,解得.
故答案为:.
作出函数的图象,可得最小值为0,最大值为2,由基本不等式可得的最小值为,由题意可得,解不等式即可得到所求范围.
本题考查分段函数的图象及应用,考查基本不等式的运用:求最值,注意数形结合思想方法的运用,属于中档题.
17.【答案】1
【解析】
【分析】
本题考查分段函数的图象和运用,主要考查函数的对称性和对数的运算性质,正确画图和通过图象观察是解题的关键.
作出函数的图象,令,设,由图象的对称性可得,
由条件可得由,即可得到m的值.
【解答】
解:作出函数的图象,
令,设,
则有,
由的取值范围为,
则,即.
由图可知,即有,,
解得.
故答案为1.
18.【答案】0或
【解析】解:若时,由已知可得,,
解可得,,
当时,由已知可得,
,
解可得,
故答案为:0或
由已知结合x的范围可得的解析式,然后结合已知方程可求满足条件的x.
本题主要考查了分段函数的函数解析式的应用,解题的关键是确定不同的x所对应的不同函数解析式.
19.【答案】解:依题意,得当时,;
当时,,
当,N时,.
当时,取得最大值,.
当,时,
,
当或58时,取得最大值,.
,
当公司参加培训的员工人数为57或58时,培训机构可获得最大利润元.
【解析】本题考查了二次函数模型、分段函数模型的相关知识,试题难度一般
20.【答案】解:依题意,当且
N时,,
当且
N时,,
当且
N时,,
当时,.
当且
N时,,
当时,.
,当年产量为80件时,利润最大,为万元.
【解析】本题考查了分段函数模型、函数模型的应用的相关知识,试题难度一般
21.【答案】解:由已知
即
答:的函数关系式为
由变形得
,
当时,在上单调递减,在上单调递增,
且
;
当时,,
当且仅当时,即时等号成立.
,
因为,所以当时,.
答:当投入的肥料费用为30元时,种植该果树获得的最大利润是270元.
【解析】本题考查了函数的应用、基本不等式的性质,考查了推理能力与计算能力,属于中档题.
由题意分段列出函数的解析式即可;
分两段讨论分别求出其最值,再取较大值即可.
22.【答案】解:当时,
当时,
所以;
当时,,
当时,,
当时,,
所以当时,
答:当产量x为300台时,公司获利润最大,最大利润为25000元.
【解析】本题考查函数模型的应用:生活中利润最大化问题.函数模型为分段函数,求分段函数的最值,应先求出函数在各部分的最值,然后取各部分的最值的最大值为整个函数的最大值,取各部分的最小者为整个函数的最小值.
利润收益成本,由已知分两段当时,和当时,求出利润函数的解析式;
分段求最大值,两者大者为所求利润最大值.
23.【答案】解:因为每件商品售价为6元,则x万件商品销售收入为6x万元,
依题意得:当时,,
当时,,
所以,
当时,,
当时,取得最大值万元,
当时,,
当且仅当,即时,取等号.
即时,取得最大值15万元,
因为,
所以当年产量为10万件时,小王在这一商品的生产中所获利润最大,最大利润为15万元.
【解析】本题考查分段函数模型的应用,二次函数的性质和基本不等式的应用,属于中档题.
根据题意对x分类讨论,可得分段函数解析式;
利用二次函数的性质和基本不等式求出各区间上函数的最值,然后比较,即可得.
第2页,共20页
第1页,共20页
一、选择题
生产一定数量的商品的全部费用称为生产成本,某企业一个月生产某种商品x万件时的生产成本为万元一万件售价是20万元,为获取更大利润,该企业一个月应生产该商品数量为
A.
36万件
B.
18万件
C.
22万件
D.
9万件
德国著名数学家狄利克雷在数学领域成就显著,以其名字命名的函数被称为狄利克雷函数,其中R为实数集,Q为有理数集,则关于狄利克雷函数给出四个命题:?
;函数是偶函数;任取一个不为零的有理数T,对任意的恒成立;存在三个点,,,使得为等边三角形.其中真命题的个数是???
A.
1
B.
2
C.
3
D.
4
某手机生产线的年固定成本为250万元,每生产x千台需另投入成本万元.当年产量不足80千台时,万元;当年产量不小于80千台时,万元,每千台产品的售价为50万元,该厂生产的产品能全部售完.当年产量为??????
千台时,该厂当年的利润最大?
A.
60
B.
80
C.
100
D.
120
某商店计划投入资金20万元经销甲或乙商品,已知经销甲商品与乙商品所获得的利润分别为P和万元,且它们与投入资金万元的关系是:,若不管资金如何投放,经销这两种商品或其中一种商品所获得的纯利润总不少于5万元,则a的最小值为?
A.
B.
5
C.
D.
某公司生产一种产品,固定成本为元,每生产一单位的产品,成本增加100元,若总收入R与年产量x的关系是则当总利润最大时,每年生产产品的单位数是?
?
A.
150
B.
200
C.
250
D.
300
若为偶函数,且当时,,则当时有
A.
B.
C.
D.
德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数被称为狄利克雷函数,其中R为实数集,Q为有理数集,则关于函数有如下四个命题:;函数是偶函数;任取一个不为零的有理数T,对任意的恒成立;存在三个点,,,使得为等边三角形.其中真命题的个数有
A.
1个
B.
2个
C.
3个
D.
4个
茶文化博大精深茶水的口感与茶叶类型和水的温度有关.经验表明,某种绿茶用的水泡制,再等到茶水温度降至时饮用,可以产生最佳口感为分析泡制一杯最佳口感茶水所需时间,某研究人员每隔测量一次茶水的温度,根据所得数据做出如图所示的散点图.观察散点图的分布情况,下列哪个函数模型可以近似地刻画茶水温度y随时间x变化的规律
A.
B.
C.
且
D.
且
为了抗击新型冠状病毒肺炎保障师生安全,我校决定每天对教室进行消毒工作,已知药物释放过程中,室内空气中的含药量与时间成正比;药物释放完毕后,y与t的函数关系式为为常数,,据测定,当空气中每立方米的含药量降低到以下时,学生方可进教室,则学校应安排工作人员至少提前?
?
分钟进行消毒工作.
A.
30
B.
40
C.
60
D.
90
某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为其中x代表拟录用人数,y代表面试人数.若面试人数为60,则该公司拟录用人数为
A.
15
B.
25
C.
40
D.
130
二、不定项选择题
“双11”购物节中,某电商对顾客实行购物优惠活动,规定一次购物付款总额满一定额度,可以给予优惠:
如果购物总额不超过50元,则不给予优惠;
如果购物总额超过50元但不超过100元,可以使用一张5元优惠券;
如果购物总额超过100元但不超过300元,则按标价给予9折优惠;
如果购物总额超过300元,其中300元内的按第条给予优惠,超过300元的部分给予8折优惠.某人购买了部分商品,则下列说法正确的是?
?
A.
如果购物总额为78元,则应付款为73元
B.
如果购物总额为228元,则应付款为元
C.
如果购物总额为368元,则应付款为元
D.
如果购物时一次性全部付款元,则购物总额为516元
某工厂生产某种产品的年固定成本为200万元,每生产x千件,需另投入成本为y万元,当年产量不足80千件时,,当年产量不小于80千件时,每件商品售价为万元,年利润为通过市场分析,该厂生产的商品能全部售完,则下列选项正确的是
A.
年利润和年产量的关系为
B.
年利润和年产量的关系为
C.
年利润最大为1050万元
D.
年利润最大为1450万元
甲同学家到乙同学家的途中有一座公园,甲同学家到公园的距离与乙同学家到公园的距离都是如图所示表示甲同学从家出发到乙同学家经过的路程与时间的关系,下列结论正确的是
A.
甲同学从家出发到乙同学家走了
B.
甲从家到公园的时间是
C.
甲从家到公园的速度比从公园到乙同学家的速度快
D.
当时,y与x的关系式为
E.
当时,y与x的关系式为
某停车场的收费标准如下:临时停车半小时内含半小时免费,临时停车1小时收费5元,此后每停车1小时收费3元,不足1小时按1小时计算,24小时内最高收费40元.现有甲、乙两车临时停放在该停车场,下列判断正确的是
A.
若甲车与乙车的停车时长之和为小时,则停车费用之和可能为8元
B.
若甲车与乙车的停车时长之和为小时,则停车费用之和可能为10元
C.
若甲车与乙车的停车时长之和为10小时,则停车费用之和可能为34元
D.
若甲车与乙车的停车时长之和为25小时,则停车费用之和可能为45元
三、填空题
已知函数,若a,b,c互不相等,且,则的取值范围为______用区间表示
设函数,函数,若存在唯一的,使得的值为,则实数a的取值范围为______.
已知函数,若?
互不相等,且的取值范围为,则实数m的值为__________________.
设函数若,则______.
四、解答题
某公司为提高员工的综合素质,聘请专业机构对员工进行专业技术培训,其中培训机构成本费用为元.公司每位员工的培训费用按以下方式与该机构结算:若公司参加培训的员工人数不超过30,则每人的培训费用为850元;若公司参加培训的员工人数多于30,则给予优惠:每多一人,每位员工的培训费减少10元.已知该公司最多有60位员工可参加培训,设参加培训的员工人数为x,每位员工的培训费用为y元,培训机构的利润为Q元.
写出y与之间的函数关系式;
当公司参加培训的员工为多少人时,培训机构可获得最大利润?并求最大利润.
某工厂某种产品的年固定成本为250万元,每生产x件,需另投入成本万元,当年产量不足80件时,,当年产量不少于80件时,,每件产品的售价为50万元,通过市场分析,该厂生产的产品能全部售完.
写出年利润万元关于年产量件的函数关系式;
当年产量为多少件时,该厂在这一产品的生产中所获利润最大?
习总书记指出:“绿水青山就是金山银山”常州市一乡镇响应号召,因地制宜的将该镇打造成“生态水果特色小镇”调研过程中发现:某珍稀水果树的单株产量单位:千克与肥料费用单位:元满足如下关系:其它成本投入如培育管理等人工费为单位:元已知这种水果的市场售价大约为10元千克,且供不应求.记该单株水果树获得的利润为单位:元.
求的函数关系式;
当投入的肥料费用为多少时,该单株水果树获得的利润最大最大利润是多少
某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足如下函数:其中x是仪器的产量.
将利润表示为产量x的函数利润总收益总成本
当产量x为何值时,公司所获利润最大?最大利润是多少元?
?为响应国家提出的“大众创业,万众创新”的号召,小王同学大学毕业后,决定利用所学专业进行自主创业.经过市场调查,生产某小型电子产品需投入年固定成本为2万元,每生产x万件,需另投入流动成本为万元.在年产量不足8万件时,万元;在年产量不小于8万件时,万元每年产品售价为6元.假设小王生产的商品当年全部售完.
??
写出年利润万元关于年产量万件的函数解析式注:年利润年销售收入固定成本流动成本;
??
年产量为多少万件时,小王在这一商品的生产中所获利润最大?最大利润是多少?
答案和解析
1.【答案】B
【解析】
【分析】
本题考查二次函数模型、二次函数的最值.根据题意,得利润函数,利用二次函数的性质,分析求得答案.
【解答】
解:根据题意,利润函数为:
,
当时,有最大值.
故选B.
2.【答案】C
【解析】
【分析】
根据函数的对应法则,可得不管x是有理数还是无理数,均有;根据函数奇偶性的定义,可得是偶函数;根据函数的表达式,结合有理数和无理数的性质可得;取,,,可得,,,三点恰好构成等边三角形.
本题给出特殊函数表达式,求函数的值并讨论它的奇偶性,着重考查了有理数、无理数的性质和函数的奇偶性等知识,属于中档题.
【解答】
解:当x为有理数时,;当x为无理数时,
当x为有理数时,;当x为无理数时,
即不管x是有理数还是无理数,均有,故不正确;
有理数的相反数还是有理数,无理数的相反数还是无理数,
对任意,都有,故正确;
若x是有理数,则也是有理数;若x是无理数,则也是无理数
根据函数的表达式,任取一个不为零的有理数T,对恒成立,故正确;
取,,,可得,,
,,,恰好为等边三角形,故正确.
故选C.
3.【答案】C
【解析】
【分析】
本题考查分段函数模型,函数的应用,属于中档题.
求出利润的函数解析式,用分段函数表示,然后分段求出函数的最大值,比较大小求解即可.
【解答】
解:?设年产量为x千台,当年的利润为y万元,
则由已知有
即
当时,由二次函数知当时,y取得最大值950,
当时,y在单调递增,在单调递减,所以当时,y取得最大值1000,
又,
所以当年产量为100千台时,该厂当年的利润取得最大值1000万元.
故选C.
4.【答案】A
【解析】
【分析】
本题考查函数最值的运用,考查学生利用数学知识解决实际问题,考查学生分析解决问题的能力,属于中档题.
设投资甲商品万元,则投资乙商品x万元,由题意,可得,时恒成立,化简求最值,即可得到结论.
【解答】
解:设投资甲商品万元,则投资乙商品x万元,
利润分别为,
时恒成立,
当时,a为一切实数
当时,分离参数得,时恒成立,
?,?
,
,
综上可得:.
所以a的最小值为,
故选A.
5.【答案】D
【解析】
【试题解析】
【分析】
本题主要考查分段函数模型的应用应用导数求实际问题中的最值问题.
根据题意得出总利润的表达式,然后利用求导得出最值得条件.
【解答】
解:由题意得,总利润?
当时,,
令,得舍负,
当时,,函数单调递增,当时,,函数单调递减,
故当时,在上取得最大值,
又当时,为减函数,
所以当每年生产300单位的产品时,总利润最大,
故选D.
6.【答案】B
【解析】
【分析】本题考查了函数的奇偶性的相关知识,试题难度较易
【解答】解:当时,,,所以,所以当时,.
故选B.
7.【答案】D
【解析】解:当x为有理数时,;当x为无理数时,
当x为有理数时,;
当x为无理数时,
即不管x是有理数还是无理数,均有,故正确;
有理数的相反数还是有理数,无理数的相反数还是无理数,
对任意,都有,故正确;
若x是有理数,则也是有理数;若x是无理数,则也是无理数
根据函数的表达式,任取一个不为零的有理数T,对恒成立,故正确;
取,,,可得,,
,,,恰好为等边三角形,故正确.
故选:D.
根据函数的对应法则,可得不管x是有理数还是无理数,均有;根据函数奇偶性的定义,可得是偶函数;根据函数的表达式,结合有理数和无理数的性质;取,,,可得,,,三点恰好构成等边三角形.
本题给出特殊函数表达式,求函数的值并讨论它的奇偶性,着重考查了有理数、无理数的性质和函数的奇偶性等知识,属于中档题.
8.【答案】C
【解析】
【分析】
本题考查函数模型的应用,属于基础题.根据散点图结合各选项中函数模型即可得出结果.
【解答】
解:选项A中,函数的图象以y轴为对称轴,不符散点图;
选项B中,函数的图象是直线,不符散点图;
选项D中,,与y轴无限接近,与散点图不符.
故选C.
9.【答案】C
【解析】
【分析】
本题考查分段函数模型,函数图像的应用,属于基础题.
由已知条件求出室内空气中的含药量关于时间的函数解析式,即可得解.
【解答】
解:根据图像:函数过点,故,
当时,取,解得,1小时分钟.
故选:C.
10.【答案】B
【解析】
【分析】本题考查了分段函数的相关知识,试题难度较易
【解答】解:令,若,则,不合题意;
若,则,满足题意;
若,则,不合题意.
故该公司拟录用25人.
11.【答案】ABD
【解析】
【试题解析】
【分析】
本题考查函数模型的应用,属于基础题.
结合购物总额对应哪种情况进行计算即可.
【解答】
解:对于A项,购物总额为78元,属于情况,可以使用一张5元优惠劵,则应付款为元,故A项正确
对于B项,购物总额为228元,属于情况,则按标价给予9折优惠,
则应付款为元,故B项正确
对于C项,购物总额为368元,属于情况,则其中300元内的按第条给予优惠,超过300元的部分给予8折优惠,故应付款为元,故C项错误
对于D项,若购物时一次性全部付款元,属于情况,
设超过300元的部分为x元,
则,解得元,则购物总额为元,故D项正确.
故选ABD.
12.【答案】AC
【解析】
【试题解析】
【分析】
本题考查分段函数模型的应用,考查二次函数以及基本不等式的应用,属于中档题.
利用条件可分别求出当80和时,万元关于年产量千件的函数解析式,利用二次函数的最值以及基本不等式,分段求解函数的最值,进而可得到结果.
【解答】
解:因为每件商品售价为万元,则x千件商品销售额为万元,依题意得:
当时,.
当时,
所以.
当时,.
此时,当时,z取得最大值万元.
当时,,
此时,即时,z取得最大值万元.
由于,
所以当年产量为100千件时,该厂在这一商品生产中所获利润最大,最大利润为1050万元.
故选AC.
13.【答案】BD
【解析】
【分析】本题考查了函数图象的应用的相关知识,试题难度较易
【解答】解:在A中,甲在公园休息的时间是,所以只走了,A错误;
由题中图象知B正确;
甲从家到公园所用的时间比从公园到乙同学家所用的时间长,而距离相等,所以甲从家到公园的速度比从公园到乙同学家的速度慢,C错误;
当时,设,则,解得,D正确;
当时,题中图象是平行于x轴的线段,E错误.
故选BD.
14.【答案】ACD
【解析】
【分析】
本题考查分段函数模型的应用,属于基础题.
根据题设中数据,即可计算出各选项的正误.
【解答】
解:若甲车停车小时,乙车停车小时,则停车费用之和为8元,A正确;
若甲车与乙车的停车时长之和为小时,则停车费用之和可能为8元或13元或16元,B错误;
若甲车与乙车都停车5小时,则停车费用之和为34元,C正确;
若甲车停车24小时,乙车停车1小时,则停车费用之和为45元,D正确.
故选ACD.
15.【答案】
【解析】解:作出函数,的图象,
不妨设,,,
,
由题意可知,
故而解得,
,
令,,则在递减,,,
,
的取值范围为,
故答案为:
先画出图象,再根据条件即可求出其范围.不妨设,利用,可得,,再构造函数,由此可确定的取值范围.
本题考查分段函数,考查绝对值函数,考查学生分析解决问题的能力,属于中档题.
16.【答案】
【解析】解:作出函数的图象,
可得的最小值为0,最大值为2;
,
当且仅当取得最小值.
由存在唯一的,使得的值
为,
可得,解得.
故答案为:.
作出函数的图象,可得最小值为0,最大值为2,由基本不等式可得的最小值为,由题意可得,解不等式即可得到所求范围.
本题考查分段函数的图象及应用,考查基本不等式的运用:求最值,注意数形结合思想方法的运用,属于中档题.
17.【答案】1
【解析】
【分析】
本题考查分段函数的图象和运用,主要考查函数的对称性和对数的运算性质,正确画图和通过图象观察是解题的关键.
作出函数的图象,令,设,由图象的对称性可得,
由条件可得由,即可得到m的值.
【解答】
解:作出函数的图象,
令,设,
则有,
由的取值范围为,
则,即.
由图可知,即有,,
解得.
故答案为1.
18.【答案】0或
【解析】解:若时,由已知可得,,
解可得,,
当时,由已知可得,
,
解可得,
故答案为:0或
由已知结合x的范围可得的解析式,然后结合已知方程可求满足条件的x.
本题主要考查了分段函数的函数解析式的应用,解题的关键是确定不同的x所对应的不同函数解析式.
19.【答案】解:依题意,得当时,;
当时,,
当,N时,.
当时,取得最大值,.
当,时,
,
当或58时,取得最大值,.
,
当公司参加培训的员工人数为57或58时,培训机构可获得最大利润元.
【解析】本题考查了二次函数模型、分段函数模型的相关知识,试题难度一般
20.【答案】解:依题意,当且
N时,,
当且
N时,,
当且
N时,,
当时,.
当且
N时,,
当时,.
,当年产量为80件时,利润最大,为万元.
【解析】本题考查了分段函数模型、函数模型的应用的相关知识,试题难度一般
21.【答案】解:由已知
即
答:的函数关系式为
由变形得
,
当时,在上单调递减,在上单调递增,
且
;
当时,,
当且仅当时,即时等号成立.
,
因为,所以当时,.
答:当投入的肥料费用为30元时,种植该果树获得的最大利润是270元.
【解析】本题考查了函数的应用、基本不等式的性质,考查了推理能力与计算能力,属于中档题.
由题意分段列出函数的解析式即可;
分两段讨论分别求出其最值,再取较大值即可.
22.【答案】解:当时,
当时,
所以;
当时,,
当时,,
当时,,
所以当时,
答:当产量x为300台时,公司获利润最大,最大利润为25000元.
【解析】本题考查函数模型的应用:生活中利润最大化问题.函数模型为分段函数,求分段函数的最值,应先求出函数在各部分的最值,然后取各部分的最值的最大值为整个函数的最大值,取各部分的最小者为整个函数的最小值.
利润收益成本,由已知分两段当时,和当时,求出利润函数的解析式;
分段求最大值,两者大者为所求利润最大值.
23.【答案】解:因为每件商品售价为6元,则x万件商品销售收入为6x万元,
依题意得:当时,,
当时,,
所以,
当时,,
当时,取得最大值万元,
当时,,
当且仅当,即时,取等号.
即时,取得最大值15万元,
因为,
所以当年产量为10万件时,小王在这一商品的生产中所获利润最大,最大利润为15万元.
【解析】本题考查分段函数模型的应用,二次函数的性质和基本不等式的应用,属于中档题.
根据题意对x分类讨论,可得分段函数解析式;
利用二次函数的性质和基本不等式求出各区间上函数的最值,然后比较,即可得.
第2页,共20页
第1页,共20页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
