华师大版九年级上册数学试题 周末作业 第24章:解直角三角形(一)(Word版 含答案)
文档属性
| 名称 | 华师大版九年级上册数学试题 周末作业 第24章:解直角三角形(一)(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 378.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 00:00:00 | ||
图片预览





文档简介
周末作业练习(一)
一、选择题(每小题5分,共30分)
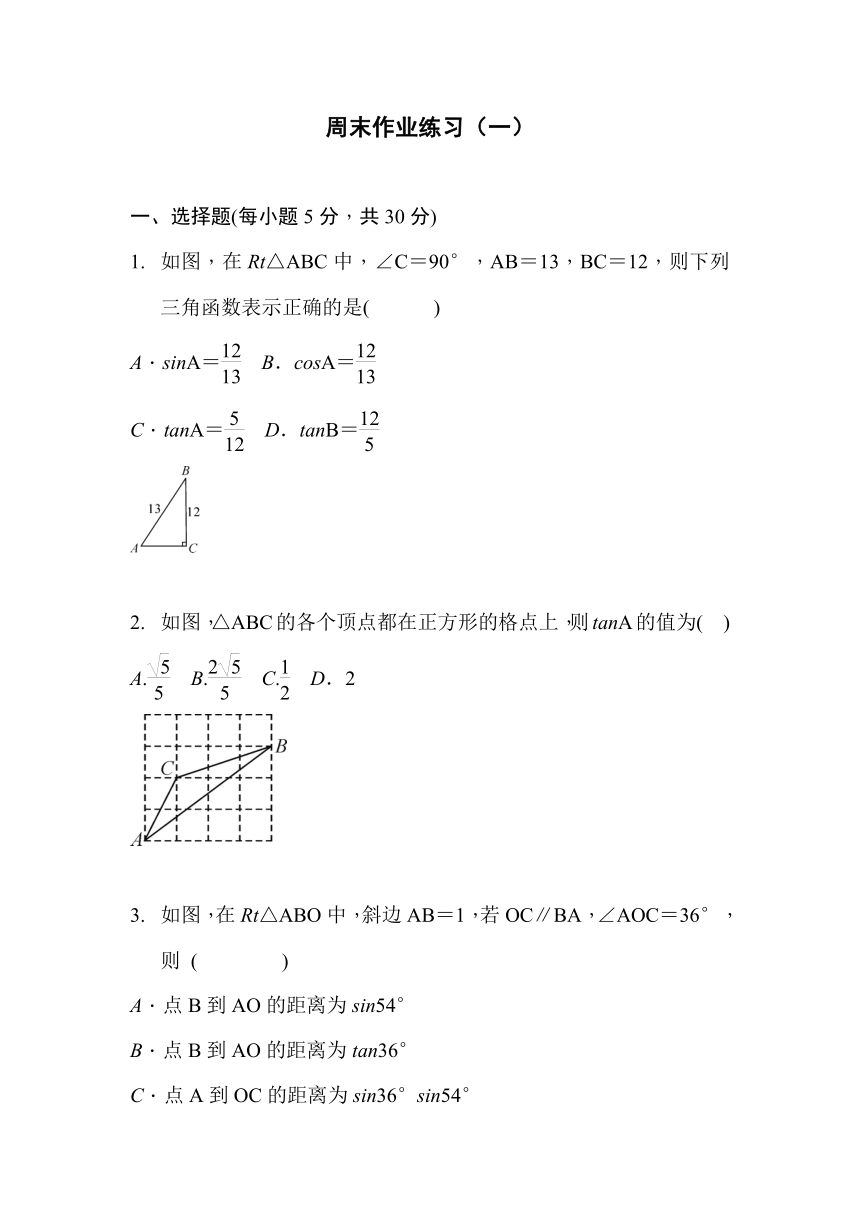
如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是(
)
A.sinA=
B.cosA=
C.tanA=
D.tanB=
如图,△ABC的各个顶点都在正方形的格点上,则tanA的值为(
)
A.
B.
C.
D.2
如图,在Rt△ABO中,斜边AB=1,若OC∥BA,∠AOC=36°,则
(
)
A.点B到AO的距离为sin54°
B.点B到AO的距离为tan36°
C.点A到OC的距离为sin36°sin54°
D.点B到AO的距离为cos36°sin54°
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60
cm长的绑绳EF,tanα=,则“人字梯”的顶端离地面的高度AD是(
)
A.144
cm
B.180
cm
C.240
cm
D.360
cm
如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角∠AED=58°,升旗台底部到教学楼底部的距离DE=7米,升旗台坡面CD的坡度i=1∶0.75,坡长CD=2米,若旗杆底部到坡面CD的水平距离BC=1米,则旗杆AB的高度约为(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6)(
)
A.12.6米
B.13.1米
C.14.7米
D.16.3米
一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位,参考数据:≈1.732,≈1.414)(
)
A.4.64海里
B.5.49海里
C.6.12海里
D.6.21海里
二、填空题(每小题5分,共30分)
在Rt△ABC中,∠ABC=90°,AB=3,BC=4,则sinA=
.
如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD=
.
,第8题图)
如图,在?ABCD中,AE⊥BD于点E,∠EAC=30°,AE=3,则AC的长等于
.
,第9题图)
如图,在点B处测得塔顶A的仰角为30°,点B到塔底C的水平距离BC是30
m,那么塔AC的高度为
m(结果保留根号).
如图,某公园入口原有一段台阶,其倾角∠BAE=30°,高DE=2
m,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起点为C,现设计斜坡BC的坡度i=1∶5,则AC的长度是
m.
,第11题图)
如图,在△ABC中,AB=AC,腰上的高BD=2,底边上的高AE=4,则tanC的值为
.
,第12题图)
三、解答题(共52分)
(10分)计算:sin45°+cos230°-+2sin60°.
(20分)如图,已知△ABC中,AB=BC=5,tan∠ABC=.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
(20分)如图为某景区五个景点A,B,C,D,E的平面示意图,B,A在C的正东方向,D在C的正北方向,D,E在B的北偏西30°方向上,E在A的西北方向上,C,D相距1000
m,E在BD的中点处.
(1)求景点B,E之间的距离;
(2)求景点B,A之间的距离.(结果保留根号)
(20分)在一次课外活动中,甲、乙两位同学测量公园中孔子塑像的高度,他们分别在A,B两处用高度为1.5
m的测角仪测得塑像顶部C的仰角分别为30°,45°,两人间的水平距离AB为10
m,求塑像的高度CF.(结果保留根号)
(20分)王阿姨家的阳台上放置了一个晾衣架,完全稳固张开如图①.图②,图③是晾衣架的侧面展开图,△AOB是边长为130
cm的等边三角形,晾衣架OE,OF能以O为圆心转动,且OE=OF=130
cm.在OA,OB上的点C,D处分别有支撑杆CN,DM能以C,D为圆心转动.
(1)如图②,若EF平行于地面AB,王阿姨的衣服挂在衣架上的总长度是110
cm,垂挂在晾衣杆OE上是否会拖到地面上?说明理由;
(2)如图③,当支撑杆DM支到点M′,此时∠EOB=78°,点E离地面距离最大.保证衣服不拖到地面上,衣服穿在衣架上的总长度最长约为多少厘米?(结果取整,参考数据:≈,sin78°≈,cos78°≈,sin18°≈,cos18°≈)
答案:
1.
A
2.
C
3.
C
4.
B
5.
B
6.
B
7.
8.
9.
4
10.
10
11.
(10-2)
12.
13.
解:1+
14.
解:(1)如图,过点A作AE⊥BC,在Rt△ABE中,tan∠ABC==,AB=5,∴AE=3,BE=4,∴CE=BC-BE=5-4=1,在Rt△AEC中,根据勾股定理得:AC==
(2)∵DF垂直平分BC,
∴BD=CD,BF=CF=,∵tan∠DBF==,∴DF=,在Rt△BFD中,根据勾股定理得:BD==,∴AD=5-=,则=
15.
解:(1)由题意,得∠C=90°,∠CBD=60°,∠CAE=45°,∵CD=1000,∴BC==1000,∴BD=2BC=2000,
∵E在BD的中点处,∴BE=BD=1000(米)
(2)过E作EF⊥AB于F,在Rt△AEF中,EF=AF=BE·sin60°=1000×=500,在Rt△BEF中,BF=BE·cos60°=500,∴AB=AF-BF=500(-1)(米)
16.
解:∵AB=10
m,∴DE=DG+EG=10
m,在Rt△CEG中,∵∠CEG=45°,∴EG=CG,在Rt△CDG中,∵∠CDG=30°,∠DCG=60°,∴DG=CG·tan60°,则DE=CG·tan60°+CG=10
m.即DE=CG+CG=10.∴CG=5-5.由题意知:GF=1.5
m∴CF=CG+GF=5-5+1.5=5-3.5.答:塑像的高CF为(5-3.5)m
17.
解:(1)垂挂在晾衣杆OE上不会拖到地面上,理由:过O作OG⊥AB于G,∵△AOB是等边三角形,∴∠OAB=60°,∵OA=130,∴OG=OA=65≈65×≈111>110,
答:垂挂在晾衣杆OE上不会拖到地面上
(2)过O作OG⊥AB于G,延长GO交EF于H,∵EF∥AB,∴GH⊥EF,∵∠BOE=78°,∴∠HOE=180°-30°-78°=72°,∴∠E=18°,∵OE=130,∴OH=OE·sin18°≈130×=39(cm),∴HG=OH+OG=39+111=150(cm),答:服穿在衣架上的总长度最长约为150厘米
一、选择题(每小题5分,共30分)
如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是(
)
A.sinA=
B.cosA=
C.tanA=
D.tanB=
如图,△ABC的各个顶点都在正方形的格点上,则tanA的值为(
)
A.
B.
C.
D.2
如图,在Rt△ABO中,斜边AB=1,若OC∥BA,∠AOC=36°,则
(
)
A.点B到AO的距离为sin54°
B.点B到AO的距离为tan36°
C.点A到OC的距离为sin36°sin54°
D.点B到AO的距离为cos36°sin54°
如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60
cm长的绑绳EF,tanα=,则“人字梯”的顶端离地面的高度AD是(
)
A.144
cm
B.180
cm
C.240
cm
D.360
cm
如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角∠AED=58°,升旗台底部到教学楼底部的距离DE=7米,升旗台坡面CD的坡度i=1∶0.75,坡长CD=2米,若旗杆底部到坡面CD的水平距离BC=1米,则旗杆AB的高度约为(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6)(
)
A.12.6米
B.13.1米
C.14.7米
D.16.3米
一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是(结果保留小数点后两位,参考数据:≈1.732,≈1.414)(
)
A.4.64海里
B.5.49海里
C.6.12海里
D.6.21海里
二、填空题(每小题5分,共30分)
在Rt△ABC中,∠ABC=90°,AB=3,BC=4,则sinA=
.
如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD=
.
,第8题图)
如图,在?ABCD中,AE⊥BD于点E,∠EAC=30°,AE=3,则AC的长等于
.
,第9题图)
如图,在点B处测得塔顶A的仰角为30°,点B到塔底C的水平距离BC是30
m,那么塔AC的高度为
m(结果保留根号).
如图,某公园入口原有一段台阶,其倾角∠BAE=30°,高DE=2
m,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起点为C,现设计斜坡BC的坡度i=1∶5,则AC的长度是
m.
,第11题图)
如图,在△ABC中,AB=AC,腰上的高BD=2,底边上的高AE=4,则tanC的值为
.
,第12题图)
三、解答题(共52分)
(10分)计算:sin45°+cos230°-+2sin60°.
(20分)如图,已知△ABC中,AB=BC=5,tan∠ABC=.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
(20分)如图为某景区五个景点A,B,C,D,E的平面示意图,B,A在C的正东方向,D在C的正北方向,D,E在B的北偏西30°方向上,E在A的西北方向上,C,D相距1000
m,E在BD的中点处.
(1)求景点B,E之间的距离;
(2)求景点B,A之间的距离.(结果保留根号)
(20分)在一次课外活动中,甲、乙两位同学测量公园中孔子塑像的高度,他们分别在A,B两处用高度为1.5
m的测角仪测得塑像顶部C的仰角分别为30°,45°,两人间的水平距离AB为10
m,求塑像的高度CF.(结果保留根号)
(20分)王阿姨家的阳台上放置了一个晾衣架,完全稳固张开如图①.图②,图③是晾衣架的侧面展开图,△AOB是边长为130
cm的等边三角形,晾衣架OE,OF能以O为圆心转动,且OE=OF=130
cm.在OA,OB上的点C,D处分别有支撑杆CN,DM能以C,D为圆心转动.
(1)如图②,若EF平行于地面AB,王阿姨的衣服挂在衣架上的总长度是110
cm,垂挂在晾衣杆OE上是否会拖到地面上?说明理由;
(2)如图③,当支撑杆DM支到点M′,此时∠EOB=78°,点E离地面距离最大.保证衣服不拖到地面上,衣服穿在衣架上的总长度最长约为多少厘米?(结果取整,参考数据:≈,sin78°≈,cos78°≈,sin18°≈,cos18°≈)
答案:
1.
A
2.
C
3.
C
4.
B
5.
B
6.
B
7.
8.
9.
4
10.
10
11.
(10-2)
12.
13.
解:1+
14.
解:(1)如图,过点A作AE⊥BC,在Rt△ABE中,tan∠ABC==,AB=5,∴AE=3,BE=4,∴CE=BC-BE=5-4=1,在Rt△AEC中,根据勾股定理得:AC==
(2)∵DF垂直平分BC,
∴BD=CD,BF=CF=,∵tan∠DBF==,∴DF=,在Rt△BFD中,根据勾股定理得:BD==,∴AD=5-=,则=
15.
解:(1)由题意,得∠C=90°,∠CBD=60°,∠CAE=45°,∵CD=1000,∴BC==1000,∴BD=2BC=2000,
∵E在BD的中点处,∴BE=BD=1000(米)
(2)过E作EF⊥AB于F,在Rt△AEF中,EF=AF=BE·sin60°=1000×=500,在Rt△BEF中,BF=BE·cos60°=500,∴AB=AF-BF=500(-1)(米)
16.
解:∵AB=10
m,∴DE=DG+EG=10
m,在Rt△CEG中,∵∠CEG=45°,∴EG=CG,在Rt△CDG中,∵∠CDG=30°,∠DCG=60°,∴DG=CG·tan60°,则DE=CG·tan60°+CG=10
m.即DE=CG+CG=10.∴CG=5-5.由题意知:GF=1.5
m∴CF=CG+GF=5-5+1.5=5-3.5.答:塑像的高CF为(5-3.5)m
17.
解:(1)垂挂在晾衣杆OE上不会拖到地面上,理由:过O作OG⊥AB于G,∵△AOB是等边三角形,∴∠OAB=60°,∵OA=130,∴OG=OA=65≈65×≈111>110,
答:垂挂在晾衣杆OE上不会拖到地面上
(2)过O作OG⊥AB于G,延长GO交EF于H,∵EF∥AB,∴GH⊥EF,∵∠BOE=78°,∴∠HOE=180°-30°-78°=72°,∴∠E=18°,∵OE=130,∴OH=OE·sin18°≈130×=39(cm),∴HG=OH+OG=39+111=150(cm),答:服穿在衣架上的总长度最长约为150厘米
