人教版七年级数学下册9.3一元一次不等式组应用题课件(25张)
文档属性
| 名称 | 人教版七年级数学下册9.3一元一次不等式组应用题课件(25张) |
|
|
| 格式 | ppt | ||
| 文件大小 | 458.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 00:00:00 | ||
图片预览







文档简介
9.3一元一次不等式组的应用
1、什么叫一元一次不等式组?
回顾与思考
一般地,由几个一元一次不等式所组成的不等式组叫做一元一次不等式组.
2、什么叫一元一次不等式组的解集?
一般地,几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
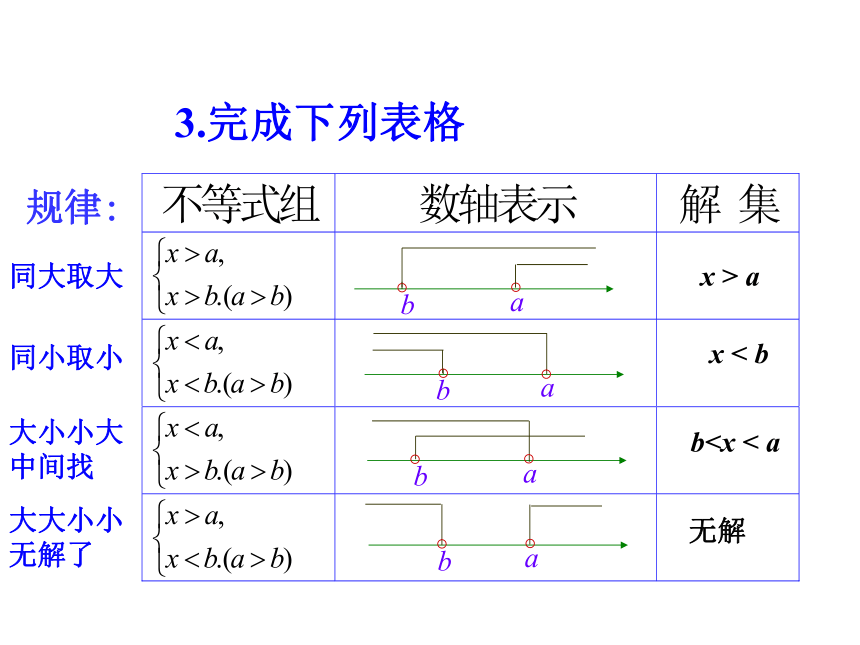
3.完成下列表格
b
a
x > a
b
a
x < b
b
a
b
a
b无解
同大取大
同小取小
大小小大
中间找
大大小小
无解了
规律:
3个小组计划在10天内生产500件产品(每天产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务;问:每个小组原先每天生产多少件产品?
合作探索
“不能完成任务”的意思是:
“提前完成任务”的意思是:
按原先的生产速度,10天的产品数量 500
提高生产速度后,10天的产品数量 500
<
>
请根据不等关系,列出不等式,
组成不等式组。
思路分析
解:设每个小组原先每天生产 件产品,
由题中不等关系得:
①
②
由不等式①得:
由不等式②得:
答:每个小组原先每天生产16件产品。
提高速度后每个小组每天生产 件产品
根据题意, 的值应是整数
一本英语书共98页,张力读了一周(7天)还没读完,而李永不到一周就已读完。李永平均每天比张力多读3页,张力平均每天读多少页?(答案取整数)
释放你的智慧!
张力7天读书的页数 < 98
李永7天读书的页数 > 98
不等关系:
解:设张力平均每天读x页
7( x +3)>98 ①
7 x <98 ②
解不等式①得
x >11
解不等式②得
x <14
因此,不等式组的解集为
11 < x<14
根据题意得,x的值应是整数,所以
x=12或13
答:张力平均每天读12或13页
在一次绿色环保知识竞赛中,共有20道题,对于每一道题,答对了得10分,答错或不答扣5分。已知小明得分在60到80分之间,那么小明答对了几道题?
释放你的智慧!
60 小明得分
小明得分 80
不等关系:
go
解:设小明答对了 道,
由题中不等关系得:
①
②
由不等式①得:
由不等式②得:
答:小明答对了11或12道.
答错了 道
go
根据题意, 的值应是整数
小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端,这时,爸爸的脚仍然着地。后来,小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果小宝和妈妈的脚着地。猜猜小宝的体重约有多少千克?
分析:从跷跷板的两种状况可以得到不等关系
妈妈的体重+小宝的体重 爸爸的体重
妈妈的体重+小宝的体重+6千克 爸爸的体重
解:设小宝的体重是x千克,则妈妈的体重是2x千克。
由题意得
<
>
2x+x<72
2x+x+6>72
解得:22(1)审 :审题,分析题目中已知什么,求什么,明确各数量之间的关系;
(2)设:设适当的未知数;
(3)找:找出题目中的所有不等关系;
(4)列:根据不等关系列出不等式组;
(5)解:求出这个不等式组的解集;
(6)答:写出符合题意的答案。
列不等式组解应用题的一般步骤:
你觉得列一元一次不等式组解应用题与列二元一次方程组解应用题的步骤一样吗?
设
找
列
解(结果
一元一次不等式组
二元一次方程组
思考:
一个未知数
两个未知数
找
不等关系
找
等量关系
一个范围
一组数
列不等
式组
列方程组
如果每个学生分3个桃子,那么多8个;如果前面每人分5个,那么最后一个人分到桃子但少于3个.试问有几个学生,几个桃子?
设有x个学生,
整理得:
解得:
∵x表示人数
(3x+8)
(3x+8)-5(x-1) <3
2x<13
2x>10
x<6.5
x>5
即:5<x<6.5
∴ 3x+8=
解:
答:共有6个学生,26个桃子。
如果每个学生分3个桃子,那么多8个;如果前面每人分5个,那么最后一个人得到桃子但少于3个.试问有几个学生,几个桃子?
则有(3x+8)个桃子.
5(x-1)
>0
-
∴x取正整数
∴ x=6
26
某班有若干学生住宿,若每间住4人,则有20人没宿舍住;若每间住8人则有一间没有住满人,试求该班宿舍间数及住宿人数?
某班有若干学生住宿,若每间住4人,则有20人没宿舍住;若每间住8人则有一间没有住满人,试求该班宿舍间数及住宿人数?
解:设有x间宿舍,则有(4x+20)人住宿,根据题意得
(4x+20)-8(x-1)>0
(4x+20)-8(x-1)<8
x<7
x>5
解得
因为宿舍间数是整数所以
x=6; 4x+20=44
答:该班有6间宿舍及44人住宿。
因此,不等式组的解集为
5 < x<7
接待一世博旅行团有290名游客,共有100件行李。计划租用甲,乙两种型号的汽车共8辆。甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李。
(1)设租用甲种汽车 辆,请你帮助设计可能的租车方案;
(2)如果甲,乙两种汽车每辆的租车费用分别为2000元,1800元,你会选择哪种租车方案。
接待一世博旅行团有290名游客,共有100件行李。计划租用甲,乙两种型号的汽车共8辆。甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李。
(1)设租用甲种汽车 辆,请你帮助设计可能的租车方案;
(2)如果甲,乙两种汽车每辆的租车费用分别为2000元,1800元,你会选择哪种租车方案。
甲汽车载人数+乙汽车载人数 290
甲汽车载行李件数+乙汽车载行李件数 100
即共有2种租车方案:
第一种是租用甲种汽车5辆,乙种汽车3辆;
第二种是租用甲种汽车6辆,乙种汽车2辆。
(2)第一种租车方案的费用为
5 ×2000+3×1800=15400元
第二种租车方案的费用为
6 ×2000+2×1800=15600元
∴ 选择第一种租车方案
分析:
解得: 5≤ ≤ 6
40 +30(8 — ) ≥ 290
10 +20(8 — ) ≥100
因为 为整数,所以 =5,6
8—
8
290
100
40
10
30(8— )
20(8— )
甲
乙
总共
车辆数
车载人数
车载行李件数
≥
≥
思考题.把价格为20元/千克的甲种糖果8千克和价格为18元/千克的乙种糖果若干千克混合,要使总价不超过400元,且糖果不少于15千克,所混合的乙种糖果最少是多少?
解:设所混合的乙种糖果有xkg.根据题意,得
解得
答:乙种糖果最少7千克.
(09广东): 1、某工人在生产中,经过第一次改进技术,每天所做的零件的个数比原来多10个,因而他在8天内做完的零件就超过200个,后来,又经过第二次技术的改进,每天又多做37个零件,这样他只做4天,所做的零件的个数就超过前8天的个数,问这位工人原先每天可做零件多少个?
思路点拨:解题时注意抓住题设中的关键字眼,“超过”、“多”。本题的关键是第二次改进后4天所做的个数就超过前8天的个数.设这个工人原先每天做x个零件,
则根据题意得
谢谢指导!
1、什么叫一元一次不等式组?
回顾与思考
一般地,由几个一元一次不等式所组成的不等式组叫做一元一次不等式组.
2、什么叫一元一次不等式组的解集?
一般地,几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
3.完成下列表格
b
a
x > a
b
a
x < b
b
a
b
a
b
同大取大
同小取小
大小小大
中间找
大大小小
无解了
规律:
3个小组计划在10天内生产500件产品(每天产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务;问:每个小组原先每天生产多少件产品?
合作探索
“不能完成任务”的意思是:
“提前完成任务”的意思是:
按原先的生产速度,10天的产品数量 500
提高生产速度后,10天的产品数量 500
<
>
请根据不等关系,列出不等式,
组成不等式组。
思路分析
解:设每个小组原先每天生产 件产品,
由题中不等关系得:
①
②
由不等式①得:
由不等式②得:
答:每个小组原先每天生产16件产品。
提高速度后每个小组每天生产 件产品
根据题意, 的值应是整数
一本英语书共98页,张力读了一周(7天)还没读完,而李永不到一周就已读完。李永平均每天比张力多读3页,张力平均每天读多少页?(答案取整数)
释放你的智慧!
张力7天读书的页数 < 98
李永7天读书的页数 > 98
不等关系:
解:设张力平均每天读x页
7( x +3)>98 ①
7 x <98 ②
解不等式①得
x >11
解不等式②得
x <14
因此,不等式组的解集为
11 < x<14
根据题意得,x的值应是整数,所以
x=12或13
答:张力平均每天读12或13页
在一次绿色环保知识竞赛中,共有20道题,对于每一道题,答对了得10分,答错或不答扣5分。已知小明得分在60到80分之间,那么小明答对了几道题?
释放你的智慧!
60 小明得分
小明得分 80
不等关系:
go
解:设小明答对了 道,
由题中不等关系得:
①
②
由不等式①得:
由不等式②得:
答:小明答对了11或12道.
答错了 道
go
根据题意, 的值应是整数
小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端,这时,爸爸的脚仍然着地。后来,小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果小宝和妈妈的脚着地。猜猜小宝的体重约有多少千克?
分析:从跷跷板的两种状况可以得到不等关系
妈妈的体重+小宝的体重 爸爸的体重
妈妈的体重+小宝的体重+6千克 爸爸的体重
解:设小宝的体重是x千克,则妈妈的体重是2x千克。
由题意得
<
>
2x+x<72
2x+x+6>72
解得:22
(2)设:设适当的未知数;
(3)找:找出题目中的所有不等关系;
(4)列:根据不等关系列出不等式组;
(5)解:求出这个不等式组的解集;
(6)答:写出符合题意的答案。
列不等式组解应用题的一般步骤:
你觉得列一元一次不等式组解应用题与列二元一次方程组解应用题的步骤一样吗?
设
找
列
解(结果
一元一次不等式组
二元一次方程组
思考:
一个未知数
两个未知数
找
不等关系
找
等量关系
一个范围
一组数
列不等
式组
列方程组
如果每个学生分3个桃子,那么多8个;如果前面每人分5个,那么最后一个人分到桃子但少于3个.试问有几个学生,几个桃子?
设有x个学生,
整理得:
解得:
∵x表示人数
(3x+8)
(3x+8)-5(x-1) <3
2x<13
2x>10
x<6.5
x>5
即:5<x<6.5
∴ 3x+8=
解:
答:共有6个学生,26个桃子。
如果每个学生分3个桃子,那么多8个;如果前面每人分5个,那么最后一个人得到桃子但少于3个.试问有几个学生,几个桃子?
则有(3x+8)个桃子.
5(x-1)
>0
-
∴x取正整数
∴ x=6
26
某班有若干学生住宿,若每间住4人,则有20人没宿舍住;若每间住8人则有一间没有住满人,试求该班宿舍间数及住宿人数?
某班有若干学生住宿,若每间住4人,则有20人没宿舍住;若每间住8人则有一间没有住满人,试求该班宿舍间数及住宿人数?
解:设有x间宿舍,则有(4x+20)人住宿,根据题意得
(4x+20)-8(x-1)>0
(4x+20)-8(x-1)<8
x<7
x>5
解得
因为宿舍间数是整数所以
x=6; 4x+20=44
答:该班有6间宿舍及44人住宿。
因此,不等式组的解集为
5 < x<7
接待一世博旅行团有290名游客,共有100件行李。计划租用甲,乙两种型号的汽车共8辆。甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李。
(1)设租用甲种汽车 辆,请你帮助设计可能的租车方案;
(2)如果甲,乙两种汽车每辆的租车费用分别为2000元,1800元,你会选择哪种租车方案。
接待一世博旅行团有290名游客,共有100件行李。计划租用甲,乙两种型号的汽车共8辆。甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李。
(1)设租用甲种汽车 辆,请你帮助设计可能的租车方案;
(2)如果甲,乙两种汽车每辆的租车费用分别为2000元,1800元,你会选择哪种租车方案。
甲汽车载人数+乙汽车载人数 290
甲汽车载行李件数+乙汽车载行李件数 100
即共有2种租车方案:
第一种是租用甲种汽车5辆,乙种汽车3辆;
第二种是租用甲种汽车6辆,乙种汽车2辆。
(2)第一种租车方案的费用为
5 ×2000+3×1800=15400元
第二种租车方案的费用为
6 ×2000+2×1800=15600元
∴ 选择第一种租车方案
分析:
解得: 5≤ ≤ 6
40 +30(8 — ) ≥ 290
10 +20(8 — ) ≥100
因为 为整数,所以 =5,6
8—
8
290
100
40
10
30(8— )
20(8— )
甲
乙
总共
车辆数
车载人数
车载行李件数
≥
≥
思考题.把价格为20元/千克的甲种糖果8千克和价格为18元/千克的乙种糖果若干千克混合,要使总价不超过400元,且糖果不少于15千克,所混合的乙种糖果最少是多少?
解:设所混合的乙种糖果有xkg.根据题意,得
解得
答:乙种糖果最少7千克.
(09广东): 1、某工人在生产中,经过第一次改进技术,每天所做的零件的个数比原来多10个,因而他在8天内做完的零件就超过200个,后来,又经过第二次技术的改进,每天又多做37个零件,这样他只做4天,所做的零件的个数就超过前8天的个数,问这位工人原先每天可做零件多少个?
思路点拨:解题时注意抓住题设中的关键字眼,“超过”、“多”。本题的关键是第二次改进后4天所做的个数就超过前8天的个数.设这个工人原先每天做x个零件,
则根据题意得
谢谢指导!
