沪科版(2012)初中数学八年级下册 17.4一元二次方程根与系数的关系 教案
文档属性
| 名称 | 沪科版(2012)初中数学八年级下册 17.4一元二次方程根与系数的关系 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 196.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-08 21:59:02 | ||
图片预览

文档简介
《17.4
一元二次方程的根与系数的关系》
教学目标:
知识与技能:掌握一元二次方程根和系数的关系,能不解方程求出一元二次方程的两根和与两根积.能利用一元二次方程根与系数的关系来判断已知两数是否是原方程的根,能灵活解决一些简单的有关一元二次方程的问题.
过程与方法:经过小组讨论和从特殊到一般的数学认知过程的体会.
情感态度价值观:利用韦达定理,激发学生发现问题,提高学生解决问题的能力培养学生主动探索,敢于实践,善于发现的科学精神和合作精神.
教学重点:
结合实践与探索,让学生经历和体验数学发现的过程,通过观察、实验、分析、归纳等数学思维活动,得到一元二次方程的根与系数关系的简单形式.
教学难点:
在通过具体实例获取数学发现后,引导学生通过一般形式给予证明,以及对一元二次方程根与系数的关系的熟练应用。
教学方法:发现引导法,讲练结合法
教学过程:
1、复习旧知
1、一元二次方程的一般式?
)
2、一元二次方程的求根公式?
3、一元二次方程根的情况怎样确定?
{
2、
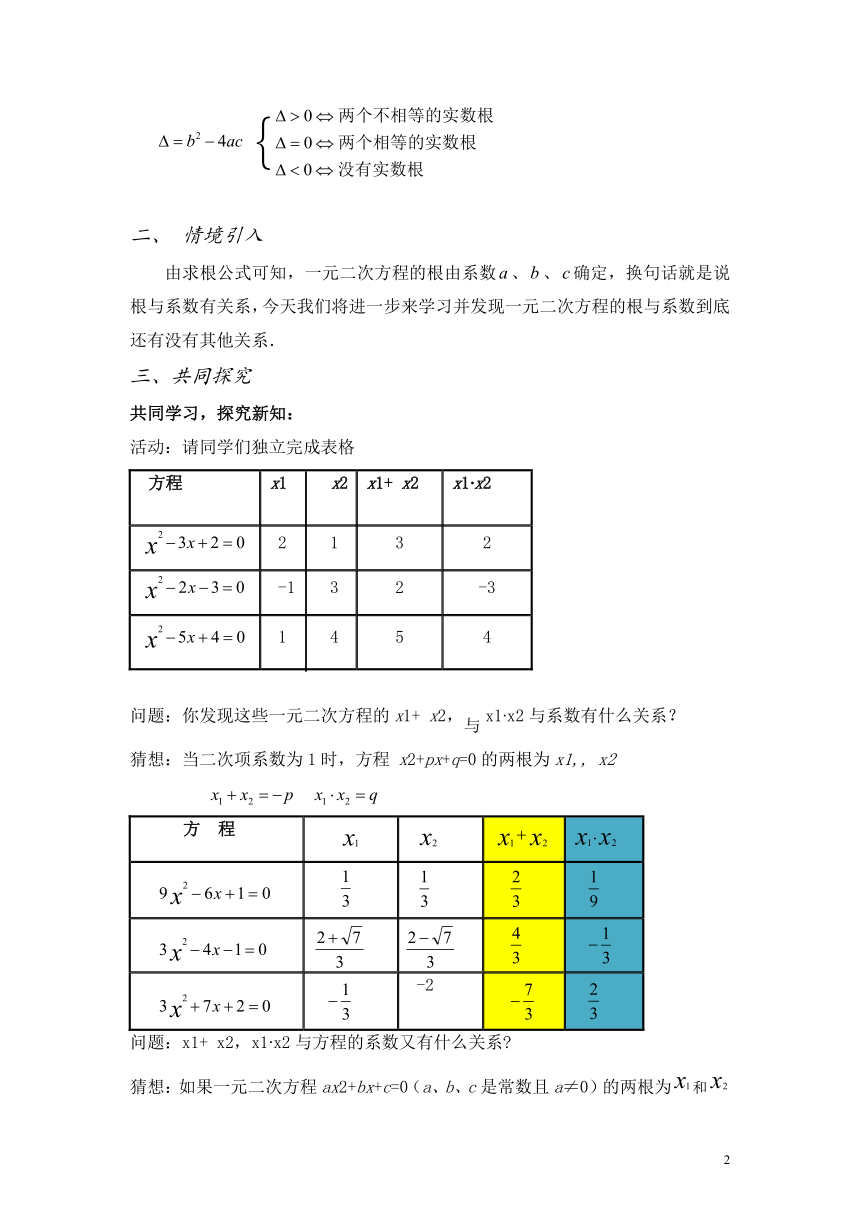
情境引入
由求根公式可知,一元二次方程的根由系数、、确定,换句话就是说根与系数有关系,今天我们将进一步来学习并发现一元二次方程的根与系数到底还有没有其他关系.
三、共同探究
共同学习,探究新知:
活动:请同学们独立完成表格
方程
x1
x2
x1+
x2
x1?x2
2
1
3
2
-1
3
2
-3
1
4
5
4
问题:你发现这些一元二次方程的x1+
x2,与x1?x2与系数有什么关系?
猜想:当二次项系数为1时,方程
x2+px+q=0的两根为x1,,
x2
方
程
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?-2
?
?
问题:x1+
x2,x1?x2与方程的系数又有什么关系?
猜想:如果一元二次方程ax2+bx+c=0(a、b、c是常数且a≠0)的两根为和则:
论证韦达定理
思考:刚才列举了部分方程发现两根和、两根积与系数有这样的关系,那么是不是所有的一元二次方程根与系数都有关系呢?
猜想:若,,(假设成立),则,.
证明:由求根根式,
∴
特别地,如果方程x2+px+q=0有两个根是x1,x2
那么有
x1+
x2=-p,
x1
?x2=q.
归纳:这就是一元二次方程根与系数的关系,也称韦达定理,因为是法国数学家韦达最先发现的.
注意:韦达定理使用前提条件1、a≠0;2、
典例分析,运用新知
例1.已知方程
x2-(k+1)x+3k=0
的一个根是2,求它的另一个根和
k
的值.
(板书解析)
例2:方程
的两根记作
,不解方程,求下面代数式的值
(1)
(2)
解:由根与系数关系得:
(2)
(1)
四、巩固练习
随堂练习,巩固新知
完成随堂练习(二)
五、课堂小结
1、若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1
、x2,则x1+x2=
,
x1x2=
.
2、用根与系数关系解题的条件是:
(1)a≠0
(2)△≥0
六、拓展提高
(思考题)已知方程
有两个正根
,求m的取值范围。
七、作业布置
必做题:
1
课本P40习题17.4
5题(做在书上)
2
同步练习P33
基础练习17.4(一)
板书设计
17.4一元二次方程根与系数的关系
1、如果一元二次方程的两根分别为x1,x2
那么,
韦达定理
特别地,若方程x2+px+q=0有两个根是x1,x2
那么有
x1+
x2=-p,
x1.x2=q.
2、根系关系使用前提条件:
a≠0;
学生课堂练习
(一)试一试
直接说出下列各方程的两根之和与两根之积:
(1)
(2)
(3)
(4)
(二)
1.已知方程
的一个根是1,求它的另一个根及
m的值.
2.设
x1,x2
是方程
的两个根,利用根与系数的关系,求下列各式的值.
(1)
(2)
(3)
(三)
思考题:已知方程
有两个正根,求m的取值范围.
PAGE
4
一元二次方程的根与系数的关系》
教学目标:
知识与技能:掌握一元二次方程根和系数的关系,能不解方程求出一元二次方程的两根和与两根积.能利用一元二次方程根与系数的关系来判断已知两数是否是原方程的根,能灵活解决一些简单的有关一元二次方程的问题.
过程与方法:经过小组讨论和从特殊到一般的数学认知过程的体会.
情感态度价值观:利用韦达定理,激发学生发现问题,提高学生解决问题的能力培养学生主动探索,敢于实践,善于发现的科学精神和合作精神.
教学重点:
结合实践与探索,让学生经历和体验数学发现的过程,通过观察、实验、分析、归纳等数学思维活动,得到一元二次方程的根与系数关系的简单形式.
教学难点:
在通过具体实例获取数学发现后,引导学生通过一般形式给予证明,以及对一元二次方程根与系数的关系的熟练应用。
教学方法:发现引导法,讲练结合法
教学过程:
1、复习旧知
1、一元二次方程的一般式?
)
2、一元二次方程的求根公式?
3、一元二次方程根的情况怎样确定?
{
2、
情境引入
由求根公式可知,一元二次方程的根由系数、、确定,换句话就是说根与系数有关系,今天我们将进一步来学习并发现一元二次方程的根与系数到底还有没有其他关系.
三、共同探究
共同学习,探究新知:
活动:请同学们独立完成表格
方程
x1
x2
x1+
x2
x1?x2
2
1
3
2
-1
3
2
-3
1
4
5
4
问题:你发现这些一元二次方程的x1+
x2,与x1?x2与系数有什么关系?
猜想:当二次项系数为1时,方程
x2+px+q=0的两根为x1,,
x2
方
程
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?-2
?
?
问题:x1+
x2,x1?x2与方程的系数又有什么关系?
猜想:如果一元二次方程ax2+bx+c=0(a、b、c是常数且a≠0)的两根为和则:
论证韦达定理
思考:刚才列举了部分方程发现两根和、两根积与系数有这样的关系,那么是不是所有的一元二次方程根与系数都有关系呢?
猜想:若,,(假设成立),则,.
证明:由求根根式,
∴
特别地,如果方程x2+px+q=0有两个根是x1,x2
那么有
x1+
x2=-p,
x1
?x2=q.
归纳:这就是一元二次方程根与系数的关系,也称韦达定理,因为是法国数学家韦达最先发现的.
注意:韦达定理使用前提条件1、a≠0;2、
典例分析,运用新知
例1.已知方程
x2-(k+1)x+3k=0
的一个根是2,求它的另一个根和
k
的值.
(板书解析)
例2:方程
的两根记作
,不解方程,求下面代数式的值
(1)
(2)
解:由根与系数关系得:
(2)
(1)
四、巩固练习
随堂练习,巩固新知
完成随堂练习(二)
五、课堂小结
1、若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1
、x2,则x1+x2=
,
x1x2=
.
2、用根与系数关系解题的条件是:
(1)a≠0
(2)△≥0
六、拓展提高
(思考题)已知方程
有两个正根
,求m的取值范围。
七、作业布置
必做题:
1
课本P40习题17.4
5题(做在书上)
2
同步练习P33
基础练习17.4(一)
板书设计
17.4一元二次方程根与系数的关系
1、如果一元二次方程的两根分别为x1,x2
那么,
韦达定理
特别地,若方程x2+px+q=0有两个根是x1,x2
那么有
x1+
x2=-p,
x1.x2=q.
2、根系关系使用前提条件:
a≠0;
学生课堂练习
(一)试一试
直接说出下列各方程的两根之和与两根之积:
(1)
(2)
(3)
(4)
(二)
1.已知方程
的一个根是1,求它的另一个根及
m的值.
2.设
x1,x2
是方程
的两个根,利用根与系数的关系,求下列各式的值.
(1)
(2)
(3)
(三)
思考题:已知方程
有两个正根,求m的取值范围.
PAGE
4
