9.5三角形的中位线-江苏省新沂市钟吾中学苏科版八年级数学下册导学案含答案
文档属性
| 名称 | 9.5三角形的中位线-江苏省新沂市钟吾中学苏科版八年级数学下册导学案含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 79.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-09 19:15:45 | ||
图片预览


文档简介
钟吾中学八年级(下)数学导学案
课题 三角形中位线 课型 新授课 章节 9.5
时间
课时 第 课时
(一)预学导航 学习目标:
经历三角形中位线及其性质的探索过程,感受转化的思想,
掌握三角形的中位线的性质;
2.会用三角形中位线定理解决有关问题.
学习重点:三角形中位线性质及应用
(二)预学成果
1.预学作业:
(1)三角形中位线的定义:____________________三角形的中位线.
(2)三角形中位线的性质:如图:DE是△ABC的中位线,则 .
2.预学检测:
(1)如图,D、E、F分别是△ABC各边的中点,如果EF=4cm,
那么BC=______m;如果AB=10cm,那么DF=_______cm;
中线AD与中位线EF的关系是_______.
已知一个三角形各边中点为顶点的三角形周长为8cm,
则原三角形的周长为 cm.
3.预学质疑:通过对本节课的预习你还有哪有疑惑?
个性补充
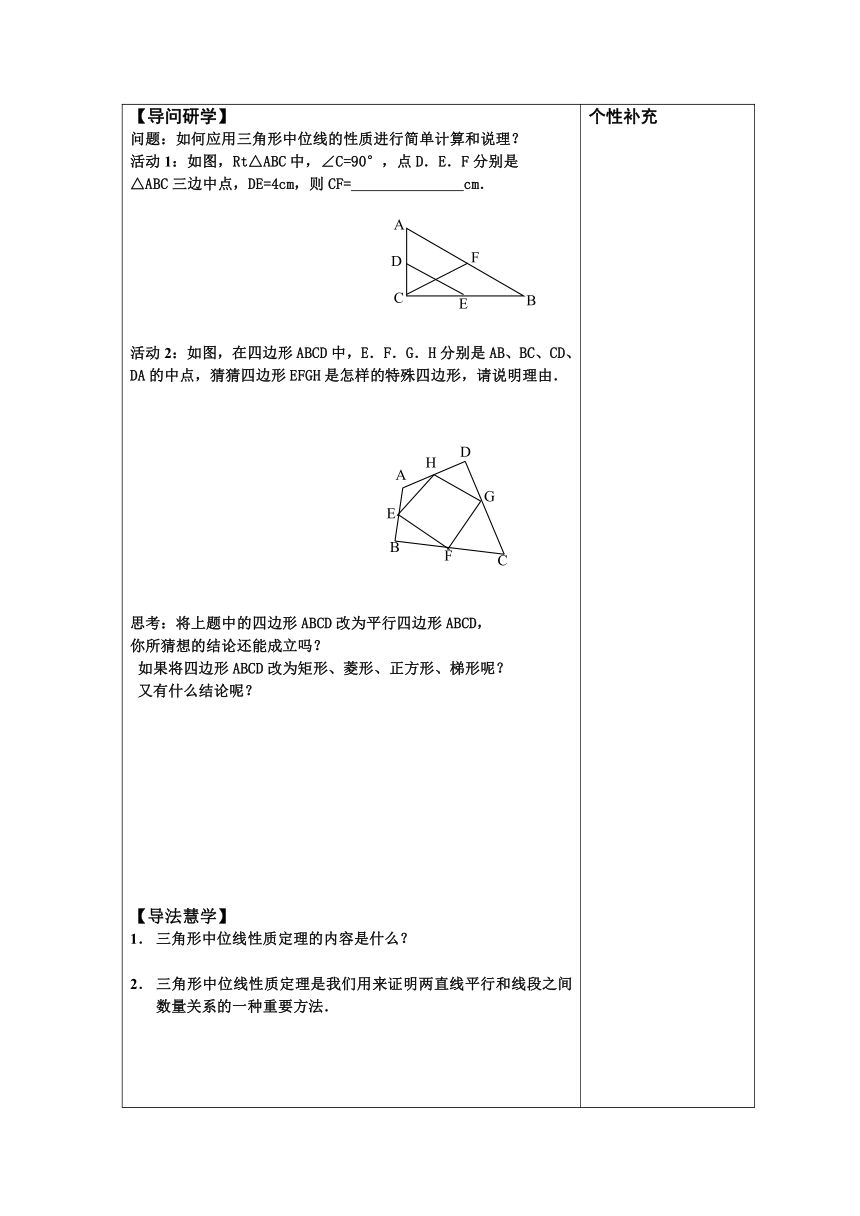
【导问研学】 问题:如何应用三角形中位线的性质进行简单计算和说理?
活动1:如图,Rt△ABC中,∠C=90°,点D.E.F分别是
△ABC三边中点,DE=4cm,则CF= cm.
活动2:如图,在四边形ABCD中,E.F.G.H分别是AB、BC、CD、DA的中点,猜猜四边形EFGH是怎样的特殊四边形,请说明理由.
思考:将上题中的四边形ABCD改为平行四边形ABCD,
你所猜想的结论还能成立吗?
如果将四边形ABCD改为矩形、菱形、正方形、梯形呢?
又有什么结论呢?
【导法慧学】
三角形中位线性质定理的内容是什么?
三角形中位线性质定理是我们用来证明两直线平行和线段之间数量关系的一种重要方法.
个性补充
【导评促学】 1.顺次连结下列各四边形中点所得的四边形是矩形的是( )
A.等腰梯形 B.矩形 C.平行四边形
D.菱形或对角线互相垂直的四边形
2.已知三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是( ).
A.3cm B.26cm C.24cm D.65cm
3.已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,
垂足是E,F是BC的中点,试说明BD=2EF
4.如图,矩形ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点,四边形EFGH是矩形吗?为什么
5.如图,在平行四边形ABCD中,E.F分别是BC.AD的中点,AE与BF相交于点G,DE与CF相交于点H,试说明GH∥AD且GH=AD
个性补充
教学反思
钟吾中学八年级(下)数学导学案
课题 三角形中位线 课型 新授课 章节 9.5
时间
课时 第 课时
(一)预学导航 学习目标:
1.经历三角形中位线及其性质的探索过程,感受转化的思想,掌握三角形的中位线的性质;
2.会用三角形中位线定理解决有关问题.
学习重点:三角形中位线性质及应用
(二)预学成果
1.预学作业:
(1)三角形中位线的定义:____________________三角形的中位线.
(2)三角形中位线的性质:如图:DE是△ABC的中位线,则 .
2.预学检测:
(1)如图,D、E、F分别是△ABC各边的中点,如果EF=4cm,那么BC=______;如果AB=10cm,那么DF=_______cm;中线AD与中位线EF的关系是_______.
(2)已知一个三角形各边中点为顶点的三角形周长为8cm,则原三角形的周长为 cm.
3.预学质疑:通过对本节课的预习你还有哪有疑惑?
个性补充
提高学生自主学习的能力
连接两边中点的线段
DE‖BC
DE=BC
8cm 5cm
互相平分
16cm
【导问研学】 问题:如何应用三角形中位线的性质进行简单计算和说理?
活动1:如图,Rt△ABC中,∠C=90°,点D.E.F分别是△ABC三边中点,DE=4cm,则CF= cm.
活动2:如图,在四边形ABCD中,E.F.G.H分别是AB、BC、CD、DA的中点,猜猜四边形EFGH是怎样的特殊四边形,请说明理由.
(思考:将上题中的四边形ABCD改为平行四边形ABCD,你所猜想的结论还能成立吗?
如果将四边形ABCD改为矩形、菱形、正方形、梯形呢?又有什么结论呢?)
【导法慧学】
三角形中位线性质定理的内容是什么?
三角形中位线性质定理是我们用来证明两直线平行和线段之间数量关系的一种重要方法.
个性补充
4cm
连接AC BD
根据中位线性质
EF‖AC HG‖AC
可得 EF‖HG
同理 EH ‖FG
四边形EFGH是平行四边形
题目综合性强
师生共同探索解题的途径
【导评促学】 1.顺次连结下列各四边形中点所得的四边形是矩形的是( )
A.等腰梯形 B.矩形 C.平行四边形
D.菱形或对角线互相垂直的四边形
2.已知三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是( ).
A.3cm B.26cm C.24cm D.65cm
3.已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E,F是BC的中点,试说明BD=2EF
4.如图,矩形ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点,四边形EFGH是矩形吗?为什么
5.如图,在平行四边形ABCD中,E.F分别是BC.AD的中点,AE与BF相交于点G,DE与CF相交于点H,试说明GH∥AD且GH=AD
个性补充
先独立完成,互相批阅,找出错误,教师点拨
C
B
由AD=AC,AE⊥CD,
等腰三角形三线合一
CE=DE 又CF=BF
所以EF是中位线
即BD=2EF
矩形ABCD
可得OA=OB=OC=OD
E,点E、F、G、H分别是OA、OB、OC、OD的中点
可得OE=OF=OH=OG
所以四边形EFGH是矩形
题目综合性强
探索解题的途径。
教学反思
课题 三角形中位线 课型 新授课 章节 9.5
时间
课时 第 课时
(一)预学导航 学习目标:
经历三角形中位线及其性质的探索过程,感受转化的思想,
掌握三角形的中位线的性质;
2.会用三角形中位线定理解决有关问题.
学习重点:三角形中位线性质及应用
(二)预学成果
1.预学作业:
(1)三角形中位线的定义:____________________三角形的中位线.
(2)三角形中位线的性质:如图:DE是△ABC的中位线,则 .
2.预学检测:
(1)如图,D、E、F分别是△ABC各边的中点,如果EF=4cm,
那么BC=______m;如果AB=10cm,那么DF=_______cm;
中线AD与中位线EF的关系是_______.
已知一个三角形各边中点为顶点的三角形周长为8cm,
则原三角形的周长为 cm.
3.预学质疑:通过对本节课的预习你还有哪有疑惑?
个性补充
【导问研学】 问题:如何应用三角形中位线的性质进行简单计算和说理?
活动1:如图,Rt△ABC中,∠C=90°,点D.E.F分别是
△ABC三边中点,DE=4cm,则CF= cm.
活动2:如图,在四边形ABCD中,E.F.G.H分别是AB、BC、CD、DA的中点,猜猜四边形EFGH是怎样的特殊四边形,请说明理由.
思考:将上题中的四边形ABCD改为平行四边形ABCD,
你所猜想的结论还能成立吗?
如果将四边形ABCD改为矩形、菱形、正方形、梯形呢?
又有什么结论呢?
【导法慧学】
三角形中位线性质定理的内容是什么?
三角形中位线性质定理是我们用来证明两直线平行和线段之间数量关系的一种重要方法.
个性补充
【导评促学】 1.顺次连结下列各四边形中点所得的四边形是矩形的是( )
A.等腰梯形 B.矩形 C.平行四边形
D.菱形或对角线互相垂直的四边形
2.已知三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是( ).
A.3cm B.26cm C.24cm D.65cm
3.已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,
垂足是E,F是BC的中点,试说明BD=2EF
4.如图,矩形ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点,四边形EFGH是矩形吗?为什么
5.如图,在平行四边形ABCD中,E.F分别是BC.AD的中点,AE与BF相交于点G,DE与CF相交于点H,试说明GH∥AD且GH=AD
个性补充
教学反思
钟吾中学八年级(下)数学导学案
课题 三角形中位线 课型 新授课 章节 9.5
时间
课时 第 课时
(一)预学导航 学习目标:
1.经历三角形中位线及其性质的探索过程,感受转化的思想,掌握三角形的中位线的性质;
2.会用三角形中位线定理解决有关问题.
学习重点:三角形中位线性质及应用
(二)预学成果
1.预学作业:
(1)三角形中位线的定义:____________________三角形的中位线.
(2)三角形中位线的性质:如图:DE是△ABC的中位线,则 .
2.预学检测:
(1)如图,D、E、F分别是△ABC各边的中点,如果EF=4cm,那么BC=______;如果AB=10cm,那么DF=_______cm;中线AD与中位线EF的关系是_______.
(2)已知一个三角形各边中点为顶点的三角形周长为8cm,则原三角形的周长为 cm.
3.预学质疑:通过对本节课的预习你还有哪有疑惑?
个性补充
提高学生自主学习的能力
连接两边中点的线段
DE‖BC
DE=BC
8cm 5cm
互相平分
16cm
【导问研学】 问题:如何应用三角形中位线的性质进行简单计算和说理?
活动1:如图,Rt△ABC中,∠C=90°,点D.E.F分别是△ABC三边中点,DE=4cm,则CF= cm.
活动2:如图,在四边形ABCD中,E.F.G.H分别是AB、BC、CD、DA的中点,猜猜四边形EFGH是怎样的特殊四边形,请说明理由.
(思考:将上题中的四边形ABCD改为平行四边形ABCD,你所猜想的结论还能成立吗?
如果将四边形ABCD改为矩形、菱形、正方形、梯形呢?又有什么结论呢?)
【导法慧学】
三角形中位线性质定理的内容是什么?
三角形中位线性质定理是我们用来证明两直线平行和线段之间数量关系的一种重要方法.
个性补充
4cm
连接AC BD
根据中位线性质
EF‖AC HG‖AC
可得 EF‖HG
同理 EH ‖FG
四边形EFGH是平行四边形
题目综合性强
师生共同探索解题的途径
【导评促学】 1.顺次连结下列各四边形中点所得的四边形是矩形的是( )
A.等腰梯形 B.矩形 C.平行四边形
D.菱形或对角线互相垂直的四边形
2.已知三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是( ).
A.3cm B.26cm C.24cm D.65cm
3.已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E,F是BC的中点,试说明BD=2EF
4.如图,矩形ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点,四边形EFGH是矩形吗?为什么
5.如图,在平行四边形ABCD中,E.F分别是BC.AD的中点,AE与BF相交于点G,DE与CF相交于点H,试说明GH∥AD且GH=AD
个性补充
先独立完成,互相批阅,找出错误,教师点拨
C
B
由AD=AC,AE⊥CD,
等腰三角形三线合一
CE=DE 又CF=BF
所以EF是中位线
即BD=2EF
矩形ABCD
可得OA=OB=OC=OD
E,点E、F、G、H分别是OA、OB、OC、OD的中点
可得OE=OF=OH=OG
所以四边形EFGH是矩形
题目综合性强
探索解题的途径。
教学反思
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
