人教版数学八年级下册第十六章二次根式知识点及经典习题(无答案)
文档属性
| 名称 | 人教版数学八年级下册第十六章二次根式知识点及经典习题(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 531.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-10 13:25:51 | ||
图片预览




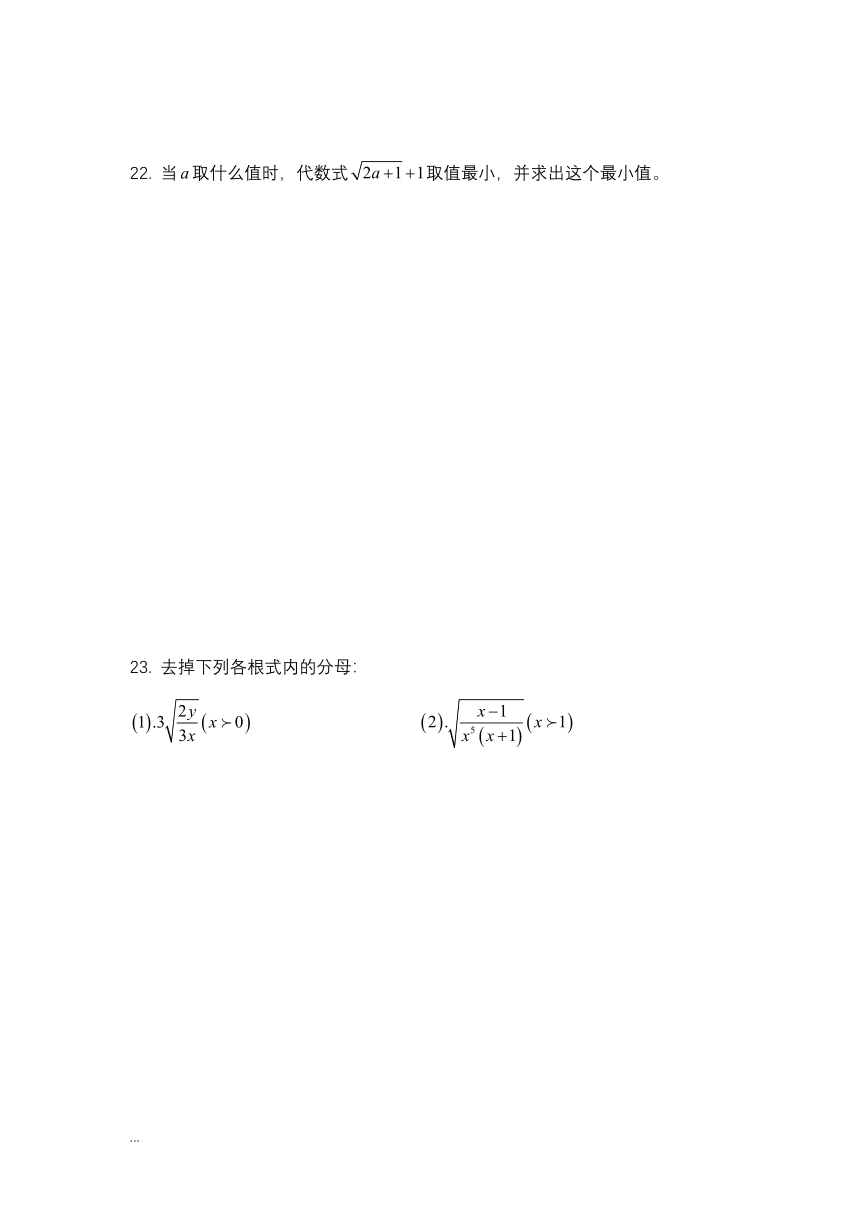
文档简介
二次根式的知识点汇总
知识点一:
二次根式的概念
形如()的式子叫做二次根式。
注:在二次根式中,被开放数可以是数,也可以是单项式、多项式、分式等代数式,但必须注意:因为负数没有平方根,所以是为二次根式的前提条件,如,,等是二次根式,而,等都不是二次根式。
知识点二:取值范围
1.???
二次根式有意义的条件:由二次根式的意义可知,当a≧0时,有意义,是二次根式,所以要使二次根式有意义,只要使被开方数大于或等于零即可。
2.???
二次根式无意义的条件:因负数没有算术平方根,所以当a﹤0时,没有意义。
知识点三:二次根式()的非负性
()表示a的算术平方根,也就是说,()是一个非负数,即0()。
注:因为二次根式()表示a的算术平方根,而正数的算术平方根是正数,0的算术平方根是0,所以非负数()的算术平方根是非负数,即0(),这个性质也就是非负数的算术平方根的性质,和绝对值、偶次方类似。这个性质在解答题目时应用较多,如若,则a=0,b=0;若,则a=0,b=0;若,则a=0,b=0。
知识点四:二次根式()的性质
()
文字语言叙述为:一个非负数的算术平方根的平方等于这个非负数。
注:二次根式的性质公式()是逆用平方根的定义得出的结论。上面的公式也可以反过来应用:若,则,如:,.
知识点五:二次根式的性质
文字语言叙述为:一个数的平方的算术平方根等于这个数的绝对值。
注:
1、化简时,一定要弄明白被开方数的底数a是正数还是负数,若是正数或0,则等于a本身,即;若a是负数,则等于a的相反数-a,即;
2、中的a的取值范围可以是任意实数,即不论a取何值,一定有意义;
3、化简时,先将它化成,再根据绝对值的意义来进行化简。
知识点六:与的异同点
1、不同点:与表示的意义是不同的,表示一个正数a的算术平方根的平方,而表示一个实数a的平方的算术平方根;在中,而中a可以是正实数,0,负实数。但与都是非负数,即,。因而它的运算的结果是有差别的,?,而
2、相同点:当被开方数都是非负数,即时,=;时,无意义,而.
二次根式
21.1
二次根式:
1.
使式子有意义的条件是
。
2.
当时,有意义。
3.
若有意义,则的取值范围是
。
4.
当时,是二次根式。
5.
在实数范围内分解因式:。
6.
若,则的取值范围是
。
7.
已知,则的取值范围是
。
8.
化简:的结果是
。
9.
当时,。
10.
把的根号外的因式移到根号内等于
。
11.
使等式成立的条件是
。
12.
若与互为相反数,则。
13.
在式子中,二次根式有(
)
A.
2个
B.
3个
C.
4个
D.
5个
14.
下列各式一定是二次根式的是(
)
A.
B.
C.
D.
15.
若,则等于(
)
A.
B.
C.
D.
16.
若,则(
)
A.
B.
C.
D.
17.
若,则化简后为(
)
A.
B.
C.
D.
18.
能使等式成立的的取值范围是(
)
A.
B.
C.
D.
19.
计算:的值是(
)
A.
0
B.
C.
D.
或
20.
下面的推导中开始出错的步骤是(
)
A.
B.
C.
D.
21.
若,求的值。
22.
当取什么值时,代数式取值最小,并求出这个最小值。
23.
去掉下列各根式内的分母:
24.
已知,求的值。
25.
已知为实数,且,求的值。
21.2
二次根式的乘除
1.
当,时,。
2.
若和都是最简二次根式,则。
3.
计算:。
4.
计算:。
5.
长方形的宽为,面积为,则长方形的长约为
(精确到0.01)。6.
下列各式不是最简二次根式的是(
)
A.
B.
C.
D.
7.
已知,化简二次根式的正确结果为(
)
A.
B.
C.
D.
8.
对于所有实数,下列等式总能成立的是(
)
A.
B.
C.
D.
9.
和的大小关系是(
)
A.
B.
C.
D.
不能确定
10.
对于二次根式,以下说法中不正确的是(
)
A.
它是一个非负数
B.
它是一个无理数
C.
它是最简二次根式
D.
它的最小值为3
11.
计算:
12.
化简:
13.
把根号外的因式移到根号内:
21.3
二次根式的加减
1.
下列根式中,与是同类二次根式的是(
)
A.
B.
C.
D.
2.
下面说法正确的是(
)
A.
被开方数相同的二次根式一定是同类二次根式
B.
与是同类二次根式
C.
与不是同类二次根式
D.
同类二次根式是根指数为2的根式
3.
与不是同类二次根式的是(
)
A.
B.
C.
D.
4.
下列根式中,是最简二次根式的是(
)
A.
B.
C.
D.
5.
若,则化简的结果是(
)
A.
B.
C.
3
D.
-3
6.
若,则的值等于(
)
A.
4
B.
C.
2
D.
7.
若的整数部分为,小数部分为,则的值是(
)
A.
B.
C.
1
D.
3
8.
下列式子中正确的是(
)
A.
B.
C.
D.
9.
在中,与是同类二次根式的是
。
10.若最简二次根式与是同类二次根式,则。
11.
一个三角形的三边长分别为,则它的周长是
cm。
12.
若最简二次根式与是同类二次根式,则。
13.
已知,则。
14.
已知,则。
15.
。
16.
计算:
⑴.
⑵.
⑶.
⑷.
17.
计算及化简:
⑴.
⑵.
⑶.
⑷.
18.
已知:,求的值。
19.
已知:,求的值。
20.
已知:为实数,且,化简:。
21.
已知的值。
PAGE
...
知识点一:
二次根式的概念
形如()的式子叫做二次根式。
注:在二次根式中,被开放数可以是数,也可以是单项式、多项式、分式等代数式,但必须注意:因为负数没有平方根,所以是为二次根式的前提条件,如,,等是二次根式,而,等都不是二次根式。
知识点二:取值范围
1.???
二次根式有意义的条件:由二次根式的意义可知,当a≧0时,有意义,是二次根式,所以要使二次根式有意义,只要使被开方数大于或等于零即可。
2.???
二次根式无意义的条件:因负数没有算术平方根,所以当a﹤0时,没有意义。
知识点三:二次根式()的非负性
()表示a的算术平方根,也就是说,()是一个非负数,即0()。
注:因为二次根式()表示a的算术平方根,而正数的算术平方根是正数,0的算术平方根是0,所以非负数()的算术平方根是非负数,即0(),这个性质也就是非负数的算术平方根的性质,和绝对值、偶次方类似。这个性质在解答题目时应用较多,如若,则a=0,b=0;若,则a=0,b=0;若,则a=0,b=0。
知识点四:二次根式()的性质
()
文字语言叙述为:一个非负数的算术平方根的平方等于这个非负数。
注:二次根式的性质公式()是逆用平方根的定义得出的结论。上面的公式也可以反过来应用:若,则,如:,.
知识点五:二次根式的性质
文字语言叙述为:一个数的平方的算术平方根等于这个数的绝对值。
注:
1、化简时,一定要弄明白被开方数的底数a是正数还是负数,若是正数或0,则等于a本身,即;若a是负数,则等于a的相反数-a,即;
2、中的a的取值范围可以是任意实数,即不论a取何值,一定有意义;
3、化简时,先将它化成,再根据绝对值的意义来进行化简。
知识点六:与的异同点
1、不同点:与表示的意义是不同的,表示一个正数a的算术平方根的平方,而表示一个实数a的平方的算术平方根;在中,而中a可以是正实数,0,负实数。但与都是非负数,即,。因而它的运算的结果是有差别的,?,而
2、相同点:当被开方数都是非负数,即时,=;时,无意义,而.
二次根式
21.1
二次根式:
1.
使式子有意义的条件是
。
2.
当时,有意义。
3.
若有意义,则的取值范围是
。
4.
当时,是二次根式。
5.
在实数范围内分解因式:。
6.
若,则的取值范围是
。
7.
已知,则的取值范围是
。
8.
化简:的结果是
。
9.
当时,。
10.
把的根号外的因式移到根号内等于
。
11.
使等式成立的条件是
。
12.
若与互为相反数,则。
13.
在式子中,二次根式有(
)
A.
2个
B.
3个
C.
4个
D.
5个
14.
下列各式一定是二次根式的是(
)
A.
B.
C.
D.
15.
若,则等于(
)
A.
B.
C.
D.
16.
若,则(
)
A.
B.
C.
D.
17.
若,则化简后为(
)
A.
B.
C.
D.
18.
能使等式成立的的取值范围是(
)
A.
B.
C.
D.
19.
计算:的值是(
)
A.
0
B.
C.
D.
或
20.
下面的推导中开始出错的步骤是(
)
A.
B.
C.
D.
21.
若,求的值。
22.
当取什么值时,代数式取值最小,并求出这个最小值。
23.
去掉下列各根式内的分母:
24.
已知,求的值。
25.
已知为实数,且,求的值。
21.2
二次根式的乘除
1.
当,时,。
2.
若和都是最简二次根式,则。
3.
计算:。
4.
计算:。
5.
长方形的宽为,面积为,则长方形的长约为
(精确到0.01)。6.
下列各式不是最简二次根式的是(
)
A.
B.
C.
D.
7.
已知,化简二次根式的正确结果为(
)
A.
B.
C.
D.
8.
对于所有实数,下列等式总能成立的是(
)
A.
B.
C.
D.
9.
和的大小关系是(
)
A.
B.
C.
D.
不能确定
10.
对于二次根式,以下说法中不正确的是(
)
A.
它是一个非负数
B.
它是一个无理数
C.
它是最简二次根式
D.
它的最小值为3
11.
计算:
12.
化简:
13.
把根号外的因式移到根号内:
21.3
二次根式的加减
1.
下列根式中,与是同类二次根式的是(
)
A.
B.
C.
D.
2.
下面说法正确的是(
)
A.
被开方数相同的二次根式一定是同类二次根式
B.
与是同类二次根式
C.
与不是同类二次根式
D.
同类二次根式是根指数为2的根式
3.
与不是同类二次根式的是(
)
A.
B.
C.
D.
4.
下列根式中,是最简二次根式的是(
)
A.
B.
C.
D.
5.
若,则化简的结果是(
)
A.
B.
C.
3
D.
-3
6.
若,则的值等于(
)
A.
4
B.
C.
2
D.
7.
若的整数部分为,小数部分为,则的值是(
)
A.
B.
C.
1
D.
3
8.
下列式子中正确的是(
)
A.
B.
C.
D.
9.
在中,与是同类二次根式的是
。
10.若最简二次根式与是同类二次根式,则。
11.
一个三角形的三边长分别为,则它的周长是
cm。
12.
若最简二次根式与是同类二次根式,则。
13.
已知,则。
14.
已知,则。
15.
。
16.
计算:
⑴.
⑵.
⑶.
⑷.
17.
计算及化简:
⑴.
⑵.
⑶.
⑷.
18.
已知:,求的值。
19.
已知:,求的值。
20.
已知:为实数,且,化简:。
21.
已知的值。
PAGE
...
